7.2.3 同角三角函数的基本关系式 课件(共19张PPT) 2024-2025学年人教B版(2019)高中数学必修第三册
文档属性
| 名称 | 7.2.3 同角三角函数的基本关系式 课件(共19张PPT) 2024-2025学年人教B版(2019)高中数学必修第三册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 954.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教B版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-01-21 22:24:34 | ||
图片预览






文档简介
(共19张PPT)
7.2.3 同角三角函数的基本关系式
人教B版(2019)必修第三册
1.理解并掌握同角三角函数的基本关系式.
2.会利用同角三角函数的基本关系式解决相关问题.
当角α取0°,30°,45°,60°时,分别计算式子sin2α+cos2α,,tan α的值.
从中你发现了什么规律
问题:sin2α+cos2α=1是否对任意角都成立 =tan α当α≠kπ+,k∈Z时是否都成立
是
如何证明呢
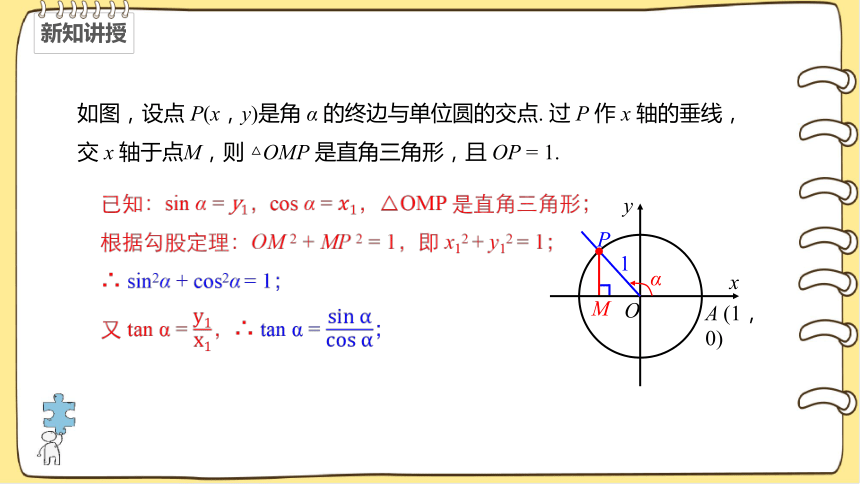
如图,设点 P(x,y)是角 α 的终边与单位圆的交点. 过 P 作 x 轴的垂线,交 x 轴于点M,则 △OMP 是直角三角形,且 OP = 1.
已知:sin α = ,cos α = ,△OMP 是直角三角形;
根据勾股定理:OM 2 + MP 2 = 1,即 x12 + y12 = 1;
∴ sin2α + cos2α = 1;
又 tan α = ,∴ tan α = ;
x
y
O
A (1,0)
α
P
1
M
同角三角函数的基本关系
平方关系:
sin2α + cos2α = 1
(当 α 的终边与坐标轴重合时,同样成立)
商数关系:
tan α =
(根据定义,当 ≠ kπ + ( k∈Z ) 才成立)
总结:同一个角 α 的正弦、余弦的平方和等于 1,商等于角 α 的正切.
例1 已知 ,求角α的余弦和正切.
解:因为,所以是第三、四象限角.
当α是第三象限角时,
,;
当α是第四象限角时,
,.
变式:已知 ,求角α的正弦和余弦.
例2 (1)已知sin α+cos α=-,0<α<π,求sin αcos α的值;
(2)已知tan α=2,求下列各式的值.
①;②2sin2α-sin αcos α+cos2α.
解:(1)由sin α+cos α=-得(sin α+cos α)2=,
sin2α+2sinαcos α+cos2α=,则sinαcos α=-.
(2)因为tan α=2,所以①==-.
②===.
1.已知三角函数值之间的关系式求其他三角函数值的问题,我们可利用平方关系或商数关系求解,其关键在于运用方程的思想及(sin α±cos α)2=1±2sin αcos α的等价转化,是分析解决问题的突破口.
方法归纳
2.已知角α的正切求关于sin α,cos α的齐次式的方法
(1)关于sin α,cos α的齐次式就是式子中的每一项都是关于sin α,cos α的式子且它们的次数之和相同,设为n次,将分子、分母同除以cos α的n次幂,其式子可化为关于tan α的式子,再代入求值.
(2)若无分母时,把分母看作1,并将1用sin2α+cos2α来代换,将分子、分母同除以cos2α,可化为关于tanα的式子,再代入求值.
例3 若sin α·tan α<0,化简.
解:∵sin α·tan α<0,∴cos α<0.
原式= +
==
==-.
1.证明恒等式的常用思路:
(1)从一边证到另一边,一般由繁到简;
(2)左右开弓,即证左边、右边都等于第三者;
(3)比较法(作差法,作比法).
2.常用的技巧:
(1)巧用“1”的代换;
(2)化切为弦;
(3)多项式运算技巧的应用(分解因式).
方法归纳
2.若α是三角形的一个内角,且sin α+cos α=,则这个三角形是( )
A.等边三角形 B.直角三角形
C.锐角三角形 D.钝角三角形
C
D
3.(多选)如果α是第二象限的角,下列各式中成立的是( )
A.tanα=- B.cos α=-
C.sinα= D.tanα=
4.若sin α+3cos α=0,则的值为________.
BC
-
根据今天所学,回答下列问题:
(1)说一说同角三角函数的基本关系
(2)上述同角三角函数的基本关系有哪些基本变形?
7.2.3 同角三角函数的基本关系式
人教B版(2019)必修第三册
1.理解并掌握同角三角函数的基本关系式.
2.会利用同角三角函数的基本关系式解决相关问题.
当角α取0°,30°,45°,60°时,分别计算式子sin2α+cos2α,,tan α的值.
从中你发现了什么规律
问题:sin2α+cos2α=1是否对任意角都成立 =tan α当α≠kπ+,k∈Z时是否都成立
是
如何证明呢
如图,设点 P(x,y)是角 α 的终边与单位圆的交点. 过 P 作 x 轴的垂线,交 x 轴于点M,则 △OMP 是直角三角形,且 OP = 1.
已知:sin α = ,cos α = ,△OMP 是直角三角形;
根据勾股定理:OM 2 + MP 2 = 1,即 x12 + y12 = 1;
∴ sin2α + cos2α = 1;
又 tan α = ,∴ tan α = ;
x
y
O
A (1,0)
α
P
1
M
同角三角函数的基本关系
平方关系:
sin2α + cos2α = 1
(当 α 的终边与坐标轴重合时,同样成立)
商数关系:
tan α =
(根据定义,当 ≠ kπ + ( k∈Z ) 才成立)
总结:同一个角 α 的正弦、余弦的平方和等于 1,商等于角 α 的正切.
例1 已知 ,求角α的余弦和正切.
解:因为,所以是第三、四象限角.
当α是第三象限角时,
,;
当α是第四象限角时,
,.
变式:已知 ,求角α的正弦和余弦.
例2 (1)已知sin α+cos α=-,0<α<π,求sin αcos α的值;
(2)已知tan α=2,求下列各式的值.
①;②2sin2α-sin αcos α+cos2α.
解:(1)由sin α+cos α=-得(sin α+cos α)2=,
sin2α+2sinαcos α+cos2α=,则sinαcos α=-.
(2)因为tan α=2,所以①==-.
②===.
1.已知三角函数值之间的关系式求其他三角函数值的问题,我们可利用平方关系或商数关系求解,其关键在于运用方程的思想及(sin α±cos α)2=1±2sin αcos α的等价转化,是分析解决问题的突破口.
方法归纳
2.已知角α的正切求关于sin α,cos α的齐次式的方法
(1)关于sin α,cos α的齐次式就是式子中的每一项都是关于sin α,cos α的式子且它们的次数之和相同,设为n次,将分子、分母同除以cos α的n次幂,其式子可化为关于tan α的式子,再代入求值.
(2)若无分母时,把分母看作1,并将1用sin2α+cos2α来代换,将分子、分母同除以cos2α,可化为关于tanα的式子,再代入求值.
例3 若sin α·tan α<0,化简.
解:∵sin α·tan α<0,∴cos α<0.
原式= +
==
==-.
1.证明恒等式的常用思路:
(1)从一边证到另一边,一般由繁到简;
(2)左右开弓,即证左边、右边都等于第三者;
(3)比较法(作差法,作比法).
2.常用的技巧:
(1)巧用“1”的代换;
(2)化切为弦;
(3)多项式运算技巧的应用(分解因式).
方法归纳
2.若α是三角形的一个内角,且sin α+cos α=,则这个三角形是( )
A.等边三角形 B.直角三角形
C.锐角三角形 D.钝角三角形
C
D
3.(多选)如果α是第二象限的角,下列各式中成立的是( )
A.tanα=- B.cos α=-
C.sinα= D.tanα=
4.若sin α+3cos α=0,则的值为________.
BC
-
根据今天所学,回答下列问题:
(1)说一说同角三角函数的基本关系
(2)上述同角三角函数的基本关系有哪些基本变形?
