7.1.1 角的推广 课件(共23张PPT)2024-2025学年人教B版(2019)高中数学必修第三册
文档属性
| 名称 | 7.1.1 角的推广 课件(共23张PPT)2024-2025学年人教B版(2019)高中数学必修第三册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 674.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教B版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-01-21 00:00:00 | ||
图片预览





文档简介
(共23张PPT)
7.1.1 角的推广
第七章 三角函数
1.理解任意角的概念.
2.理解象限角的概念.
3.能写出与任一已知角终边相同角的集合.
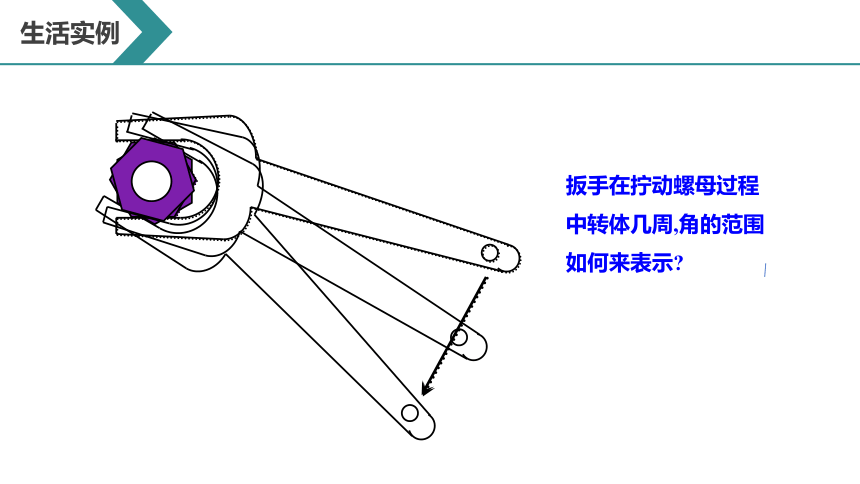
扳手在拧动螺母过程中转体几周,角的范围如何来表示
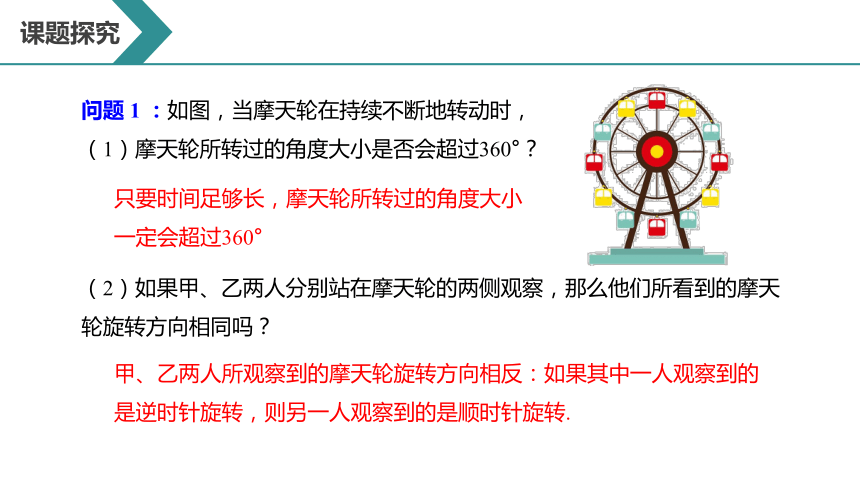
问题 1 :如图,当摩天轮在持续不断地转动时,
(1)摩天轮所转过的角度大小是否会超过360°?
只要时间足够长,摩天轮所转过的角度大小一定会超过360°
(2)如果甲、乙两人分别站在摩天轮的两侧观察,那么他们所看到的摩天轮旋转方向相同吗?
甲、乙两人所观察到的摩天轮旋转方向相反:如果其中一人观察到的是逆时针旋转,则另一人观察到的是顺时针旋转.
概念讲解
角的分类:按一条射线绕其端点的旋转方向,角可以分为三类:
正角:按逆时针方向旋转形成的角,如图∠α;
负角:按顺时针方向旋转形成的角,如图∠β ;
零角:没有做任何旋转形成的角;
O
A
B
α
正角
O1
A1
B1
β
负角
注意:如果角 α 与角 β 的旋转方向相同且旋转量相等,那么就称 α = β;
用图像表示角时,箭头的方向体现角的正负,因此箭头不能少.
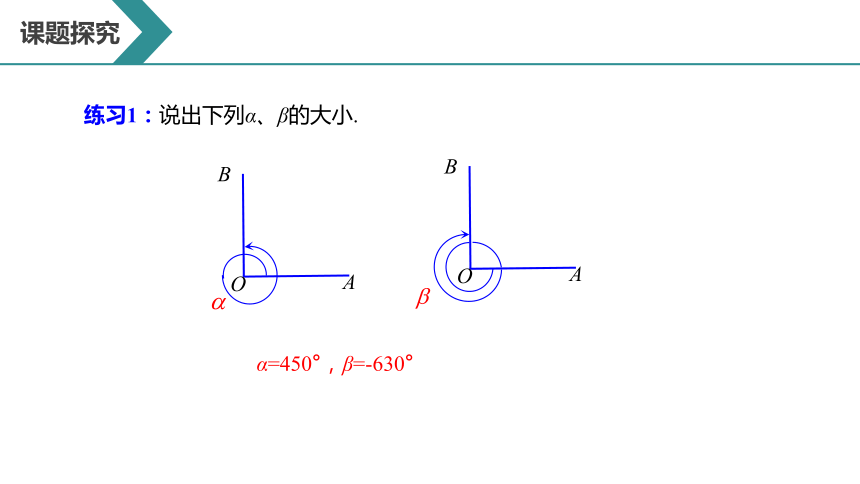
练习1:说出下列α、β的大小.
O
A
B
O
A
B
α=450°,β=-630°
问题 2 :如图,类比实数的加减运算,说说将 α 的终边再次逆时针旋转 β 后该如何表示?
α
β
把角 α 的终边旋转角 β,这时终边所对应的角是 α + β ;
思考:若将 α 的终边顺时针旋转 β 后又该如何表示?
顺时针旋转的角 β 为负角,这时终边所对应的角是 α – | β |;
注:字母 α、β 表示任意角,本身即是带有符号的.
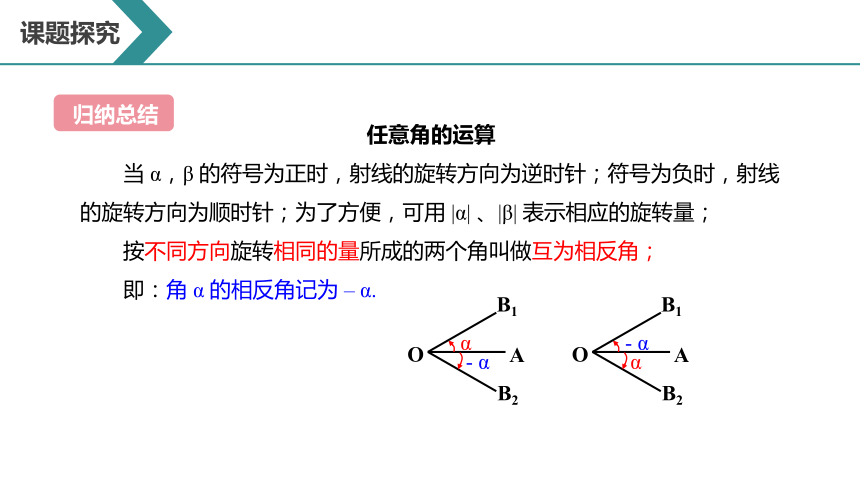
任意角的运算
当 α,β 的符号为正时,射线的旋转方向为逆时针;符号为负时,射线的旋转方向为顺时针;为了方便,可用 |α| 、|β| 表示相应的旋转量;
按不同方向旋转相同的量所成的两个角叫做互为相反角;
即:角 α 的相反角记为 – α.
O
A
B1
α
B2
- α
O
A
B1
- α
B2
α
归纳总结
练习2:射线OA绕端点O顺时针旋转80°到OB位置,接着逆时针旋转250°到OC位置,然后再顺时针旋转270°到OD位置,求∠AOD大小.
解:由题意知∠AOB=-80°,∠BOC=250°,∠COD=-270°,
因此∠AOD=∠AOB+∠BOC+∠COD =-80° + 250°-270°=-100°.
O
α = 25°
β = – 120°
x
y
问题 3 :如图,角 α 是第一象限角,角 β 是第三象限角,试计算 α + β 的值,并说说结果所得的角位于第几象限?
α + β = 25°+ (-120°) = -95°;
-95°的角位于第三象限.
象限角:将角放在平面直角坐标系中来讨论,约定:角的顶点与坐标原点重合,角的始边落在 x 轴的正半轴上,此时,角的终边在第几象限,就把这个角称为第几象限角.
思考:若角 α 的终边在坐标轴上,那么角 α 还是象限角吗?
若角的终边在坐标轴(x / y)上,那么这个角不属于任何一个象限,我们把这样的叫轴线角,如右图的角γ.
O
x
y
γ
O
x
y
B
– 30°
330°
– 390°
问题 4:分别将 30°、 – 390°及 330°的角,画在坐标系中,结合图象说说你有什么发现?
即: 30°、 – 390°及 330°是终边相同的角.
由图可知,角的终边 OB 除了可以表示 -30°的角之外,还可以表示 -390°,330°等角;
思考:结合上述问题,你发现了终边相同的角的变化规律吗?
一般地,所有与α终边相同的角,连同角α在内,可以构成一个集合:
S={ β | β = α + k·360°,k∈Z }
即:任一与 α 终边相同的角,都可以表示成角 α 与整数个周角的和.
注意:
(1)α是任意角;
(2)集合中 α 与 k·360°间用“+”连接;
如: k·360°-30°应看成 k·360°+ (-30°),表示与 -30°角终边相同的角.
概念讲解
例1 已知集合A={第一象限角},B={锐角},C={小于90°的角},则下面关系正确的是( )
A.A=B=C B.A C
C.A=B D.B
D
【解析】第一象限角可表示为k·360°<α锐角可表示为0°<β<90°;
小于90°的角可表示为γ<90°;
由三者之间的关系可知,选D.
例2 写出终边落在直线y=x上的角的集合S,并把S中适合不等式
-360°≤β<720°的元素β写出来.
解:直线y=x与x轴的夹角是45°,在[0°,360°]内,终边在直线y=x上的角有两个:45°,225°.
因此,终边在直线y=x上的角的集合:
S={β|β=45°+k·360°,k∈Z}=225°+k·360°,k∈Z}
={β|β=45°+2k·180°,k∈Z}=45°+(2k+1)·180°,k∈Z}
={β|β=45°+k·180°,k∈Z}.
所以S中适合-360°≤β<720°的元素是:
45°-2×180°=-315°;45°-1×180°=-135°;
45°+0×180°=45°;45°+1×180°=225°;
45°+2×180°=405°;45°+3×180°=585°.
例2 写出终边落在直线y=x上的角的集合S,并把S中适合不等式
-360°≤β<720°的元素β写出来.
(1)所有与角α终边相同的角,连同角α在内(而且只有这样的角),可以用式子α+k·360°,k∈Z表示.在运用时,需注意以下三点:
①k是整数,这个条件不能漏掉.
②α是任意角.
③k·360 °与α之间用“+”号连接,如k·360 °-30 °应看成k·360 °+(-30 °)(k∈Z).
(2)在0 °到360 °范围内找出与直线y=x终边相同的角,再推广到任意角.
(3)终边相同的角的取值是由k的取值决定的.
方法归纳
例3 已知,如图所示.
①分别写出终边落在OA,OB位置上的角的集合;
②写出终边落在阴影部分(包括边界)的角的集合.
{α|α=135°+k·360°,k∈Z}
{α|α=-30°+k·360°,k∈Z}
{α|-30°+k·360°≤α≤135°+k·360°,k∈Z}
变式:若将例3改为如图所示的图形,那么终边落在阴影部分(包括边界)的角的集合如何表示?
{β|k·360°+60°≤β<k·360°+105°,k∈Z}
{β|k·360°+240°≤β<k·360°+285°,k∈Z}
{β|n·180°+60°≤β<n·180°+105°,n∈Z}
起始、终止边界对应角α,β再加上360°的整数倍,即得区间角集合.
表示区间角的三个步骤
先按逆时针的方向找到区域的起始和终止边界;
第二步
按由小到大分别标出起始和终止边界对应的-360°~360°范围内的角α和β,写出最简区间{x|α第三步
第一步
方法归纳
根据今天所学,回答下列问题:
(1)按照旋转方向不同,可以将角分为几类?相等的角有什么特征?
(2)象限角是如何定义的?
(3)如何表示终边相同的角?
1.思考辨析
(1)第二象限角大于第一象限角.( )
(2)第二象限角是钝角.( )
(3)终边相同的角一定相等.( )
(4)终边相同的角有无数个,它们相差360°的整数倍.( )
×
×
×
√
2.下列各个角中与2024°终边相同的是( )
A.-154° B.684°
C.324° D.224°
3.已知角α的终边在如图阴影表示的范围内(不包含边界),那么角α的集合是 .
D
{α|k·360°+45°<α<k·360°+150°,k∈Z}
7.1.1 角的推广
第七章 三角函数
1.理解任意角的概念.
2.理解象限角的概念.
3.能写出与任一已知角终边相同角的集合.
扳手在拧动螺母过程中转体几周,角的范围如何来表示
问题 1 :如图,当摩天轮在持续不断地转动时,
(1)摩天轮所转过的角度大小是否会超过360°?
只要时间足够长,摩天轮所转过的角度大小一定会超过360°
(2)如果甲、乙两人分别站在摩天轮的两侧观察,那么他们所看到的摩天轮旋转方向相同吗?
甲、乙两人所观察到的摩天轮旋转方向相反:如果其中一人观察到的是逆时针旋转,则另一人观察到的是顺时针旋转.
概念讲解
角的分类:按一条射线绕其端点的旋转方向,角可以分为三类:
正角:按逆时针方向旋转形成的角,如图∠α;
负角:按顺时针方向旋转形成的角,如图∠β ;
零角:没有做任何旋转形成的角;
O
A
B
α
正角
O1
A1
B1
β
负角
注意:如果角 α 与角 β 的旋转方向相同且旋转量相等,那么就称 α = β;
用图像表示角时,箭头的方向体现角的正负,因此箭头不能少.
练习1:说出下列α、β的大小.
O
A
B
O
A
B
α=450°,β=-630°
问题 2 :如图,类比实数的加减运算,说说将 α 的终边再次逆时针旋转 β 后该如何表示?
α
β
把角 α 的终边旋转角 β,这时终边所对应的角是 α + β ;
思考:若将 α 的终边顺时针旋转 β 后又该如何表示?
顺时针旋转的角 β 为负角,这时终边所对应的角是 α – | β |;
注:字母 α、β 表示任意角,本身即是带有符号的.
任意角的运算
当 α,β 的符号为正时,射线的旋转方向为逆时针;符号为负时,射线的旋转方向为顺时针;为了方便,可用 |α| 、|β| 表示相应的旋转量;
按不同方向旋转相同的量所成的两个角叫做互为相反角;
即:角 α 的相反角记为 – α.
O
A
B1
α
B2
- α
O
A
B1
- α
B2
α
归纳总结
练习2:射线OA绕端点O顺时针旋转80°到OB位置,接着逆时针旋转250°到OC位置,然后再顺时针旋转270°到OD位置,求∠AOD大小.
解:由题意知∠AOB=-80°,∠BOC=250°,∠COD=-270°,
因此∠AOD=∠AOB+∠BOC+∠COD =-80° + 250°-270°=-100°.
O
α = 25°
β = – 120°
x
y
问题 3 :如图,角 α 是第一象限角,角 β 是第三象限角,试计算 α + β 的值,并说说结果所得的角位于第几象限?
α + β = 25°+ (-120°) = -95°;
-95°的角位于第三象限.
象限角:将角放在平面直角坐标系中来讨论,约定:角的顶点与坐标原点重合,角的始边落在 x 轴的正半轴上,此时,角的终边在第几象限,就把这个角称为第几象限角.
思考:若角 α 的终边在坐标轴上,那么角 α 还是象限角吗?
若角的终边在坐标轴(x / y)上,那么这个角不属于任何一个象限,我们把这样的叫轴线角,如右图的角γ.
O
x
y
γ
O
x
y
B
– 30°
330°
– 390°
问题 4:分别将 30°、 – 390°及 330°的角,画在坐标系中,结合图象说说你有什么发现?
即: 30°、 – 390°及 330°是终边相同的角.
由图可知,角的终边 OB 除了可以表示 -30°的角之外,还可以表示 -390°,330°等角;
思考:结合上述问题,你发现了终边相同的角的变化规律吗?
一般地,所有与α终边相同的角,连同角α在内,可以构成一个集合:
S={ β | β = α + k·360°,k∈Z }
即:任一与 α 终边相同的角,都可以表示成角 α 与整数个周角的和.
注意:
(1)α是任意角;
(2)集合中 α 与 k·360°间用“+”连接;
如: k·360°-30°应看成 k·360°+ (-30°),表示与 -30°角终边相同的角.
概念讲解
例1 已知集合A={第一象限角},B={锐角},C={小于90°的角},则下面关系正确的是( )
A.A=B=C B.A C
C.A=B D.B
D
【解析】第一象限角可表示为k·360°<α
小于90°的角可表示为γ<90°;
由三者之间的关系可知,选D.
例2 写出终边落在直线y=x上的角的集合S,并把S中适合不等式
-360°≤β<720°的元素β写出来.
解:直线y=x与x轴的夹角是45°,在[0°,360°]内,终边在直线y=x上的角有两个:45°,225°.
因此,终边在直线y=x上的角的集合:
S={β|β=45°+k·360°,k∈Z}=225°+k·360°,k∈Z}
={β|β=45°+2k·180°,k∈Z}=45°+(2k+1)·180°,k∈Z}
={β|β=45°+k·180°,k∈Z}.
所以S中适合-360°≤β<720°的元素是:
45°-2×180°=-315°;45°-1×180°=-135°;
45°+0×180°=45°;45°+1×180°=225°;
45°+2×180°=405°;45°+3×180°=585°.
例2 写出终边落在直线y=x上的角的集合S,并把S中适合不等式
-360°≤β<720°的元素β写出来.
(1)所有与角α终边相同的角,连同角α在内(而且只有这样的角),可以用式子α+k·360°,k∈Z表示.在运用时,需注意以下三点:
①k是整数,这个条件不能漏掉.
②α是任意角.
③k·360 °与α之间用“+”号连接,如k·360 °-30 °应看成k·360 °+(-30 °)(k∈Z).
(2)在0 °到360 °范围内找出与直线y=x终边相同的角,再推广到任意角.
(3)终边相同的角的取值是由k的取值决定的.
方法归纳
例3 已知,如图所示.
①分别写出终边落在OA,OB位置上的角的集合;
②写出终边落在阴影部分(包括边界)的角的集合.
{α|α=135°+k·360°,k∈Z}
{α|α=-30°+k·360°,k∈Z}
{α|-30°+k·360°≤α≤135°+k·360°,k∈Z}
变式:若将例3改为如图所示的图形,那么终边落在阴影部分(包括边界)的角的集合如何表示?
{β|k·360°+60°≤β<k·360°+105°,k∈Z}
{β|k·360°+240°≤β<k·360°+285°,k∈Z}
{β|n·180°+60°≤β<n·180°+105°,n∈Z}
起始、终止边界对应角α,β再加上360°的整数倍,即得区间角集合.
表示区间角的三个步骤
先按逆时针的方向找到区域的起始和终止边界;
第二步
按由小到大分别标出起始和终止边界对应的-360°~360°范围内的角α和β,写出最简区间{x|α
第一步
方法归纳
根据今天所学,回答下列问题:
(1)按照旋转方向不同,可以将角分为几类?相等的角有什么特征?
(2)象限角是如何定义的?
(3)如何表示终边相同的角?
1.思考辨析
(1)第二象限角大于第一象限角.( )
(2)第二象限角是钝角.( )
(3)终边相同的角一定相等.( )
(4)终边相同的角有无数个,它们相差360°的整数倍.( )
×
×
×
√
2.下列各个角中与2024°终边相同的是( )
A.-154° B.684°
C.324° D.224°
3.已知角α的终边在如图阴影表示的范围内(不包含边界),那么角α的集合是 .
D
{α|k·360°+45°<α<k·360°+150°,k∈Z}
