7.1.2 弧度制及其与角度制的换算 课件(共23张PPT) 2024-2025学年人教B版(2019)高中数学必修第三册
文档属性
| 名称 | 7.1.2 弧度制及其与角度制的换算 课件(共23张PPT) 2024-2025学年人教B版(2019)高中数学必修第三册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教B版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-01-21 00:00:00 | ||
图片预览








文档简介
(共23张PPT)
7.1.2 弧度制及其与角度制的换算
人教B版(2019)必修第三册
1.了解弧度制,能熟练地进行弧度制与角度制之间的换算.
2.掌握弧度制中扇形的弧长公式和面积公式.
如图是一种折叠扇.折叠扇打开、合拢的过程 可以抽象成扇形圆心角的变大、变小.那么在这个过程中,扇形的什么量在发生变化?什么量没发生变化?由此你能想到度量角的其他办法吗?
变化的量:弧长、圆心角;
没有变化的量:半径.
问题:是否可以用弧长来度量圆心角呢?
60°的圆心角,半径r为1,2,3,分别计算对应的弧长l,再计算弧长与半径的比.
猜想:圆心角不变,则弧长与半径的比值不变.
问题一般化
问题1:观察下面两图,弧AB与弧A'B'都与什么有关?
将折叠扇抽象为如图所示的图形,可以看成弧AB与弧A'B'都与角α对应,但α≠0时,它们的弧长 与 始终不相等,其原因在于OA≠OA'.
问题一般化
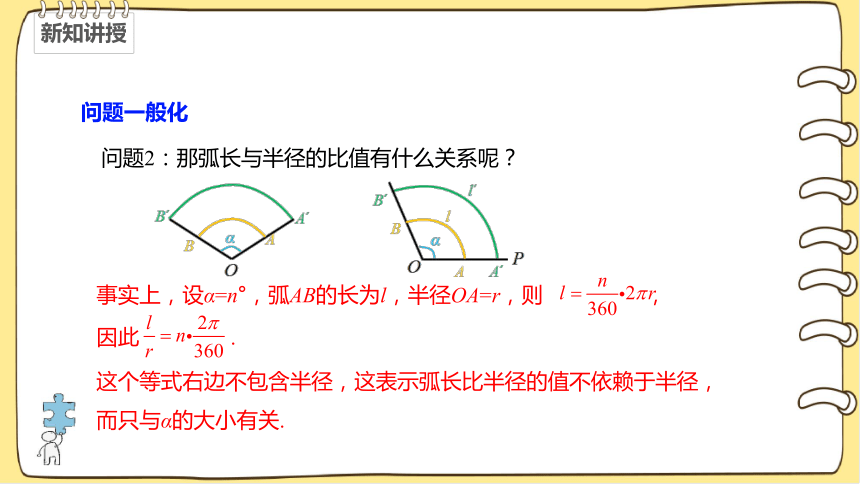
问题2:那弧长与半径的比值有什么关系呢?
事实上,设α=n°,弧AB的长为l,半径OA=r,则 ,
因此 .
这个等式右边不包含半径,这表示弧长比半径的值不依赖于半径,而只与α的大小有关.
1.弧度数定义:弧长与半径比值的这个常数为圆心角的弧度数.
2.1弧度的角:长度等于半径长的圆弧所对的圆心角为1弧度的角, 记作1 rad.
以弧度为单位来度量角的制度称为弧度制.
如图,因为 的长度等于r,所以 所对的圆心角∠AOB就是1弧度的角.
问题3:通过对比角度制与弧度制的区别与联系,完成下列表格.
弧度制 角度制
区别
联系 无论弧度制还是角度制,
角的大小都是一个与半径大小无关的定值
弧度制以线段长度来度量角
角度制是“以角量角”
弧度制是十进制
角度制是六十进制
1弧度是等于半径长的弧
所对的圆心角的大小
1°的角是周角的
问题4:按照定义,一个周角对应的弧度数应是多少?
弧度与角度如何互化呢?
答:因为半径为r的圆周长为2πr,所以圆周的弧度数是 ,
于是360°=2π rad.
180°=π rad
角度与弧度的互化
思考:某同学表示与30°角终边相同的角的集合时写成S={α|α=2kπ+30°,k∈Z},这种表示正确吗?为什么?
这种表示不正确,同一个式子中,角度、弧度不能混用,否则产生混乱,
正确的表示方法应为{α|α=2kπ+,k∈Z}或{α|α=k·360°+30°,k∈Z}.
例1 用弧度表示终边落在阴影部分内(不包括边界)的角的集合.
解:330°角的终边与-30°角的终边相同,将-30°化为弧度,即-,
而75°=75×=,
所以终边落在阴影部分内(不包括边界)的角的集合为
{θ|2kπ-<θ<2kπ+,k∈Z}.
归纳总结
1.终边相同的角
若α与β的终边相同,则β=2kπ+ α(k∈Z),前后单位要一致.
2.象限角
第一象限角的集合:{α|2kπ<α<2kπ+,k∈Z};
第二象限角的集合:{α|2kπ+<α<2kπ+π,k∈Z};
第三象限角的集合:{α|2kπ+π<α<2kπ+, k∈Z};
第四象限角的集合:{α|2kπ+<α<2kπ+2π, k∈Z}.
常用角的弧度数表示
一些特殊角与弧度数的对应关系
角度 0° 15° 30° 45° 60° 75° 90° 120° 135° 150°
弧度
角度 180° 210° 225° 240° 270° 300° 315° 330° 360°
弧度
0
π
2π
例2 设角α1=-570°,α2=750°,β1=,β2=-.
(1)将α1,α2用弧度制表示出来,并指出它们各自所在的象限;
(2)将β1,β2用角度制表示出来,并在-720°~0°之间找出与它们终边相同的所有角.
解:(1)要确定角α所在的象限,只要把α表示为α=2kπ+α0(k∈Z,0≤α0<2π)的形式,由α0所在象限即可判定出α所在的象限.
α1=-570°=-=-4π+,
α2=750°==4π+.
∴α1在第二象限,α2在第一象限.
(2)β1==108°,设θ=β1+k·360°(k∈Z),
由-720°≤θ<0°,得-720°≤108°+k·360°<0°,
∴k=-2或k=-1,
∴在-720°~0°间与β1有相同终边的角是-612°和-252°.
同理β2=-420°且在-720°~0°间与β2有相同终边的角是-60°.
例2 设角α1=-570°,α2=750°,β1=,β2=-.
(2)将β1,β2用角度制表示出来,并在-720°~0°之间找出与它们终边相同的所有角.
角度制 弧度制
弧长公式
扇形面积公式
l =
S = lR =
l = |α|·R
S = lR = ·|α|·R2
若用 R 表示圆的半径,n( 0<n<360° ),α(0<α<2π)为圆心角,l 是扇形弧长,S 是扇形面积;结合前面所学,完成下面的表格:
思考:1.用公式|α|=求圆心角时,应注意什么问题?
2.在使用弧度制下的弧长公式及面积公式时,若已知的角是以“度”为单位,需注意什么问题?
1.应注意结果是圆心角的绝对值,具体应用时既要注意其大小,又要注意其正负.
2.若已知的角是以“度”为单位,则必须先把它化成弧度后再计算,否则结果出错.
例3 设扇形的周长为8 cm,面积为4 cm2,则扇形的圆心角的弧度数是( )
A.1 rad B.2 rad
C.3 rad D.4 rad
分析 设扇形半径为r,弧长为l,由题意得解得
则圆心角α==2 rad.
B
例4 已知扇形的周长为20 cm,当它的半径和圆心角各取什么值时,才能使扇形的面积最大?最大面积是多少?
解:设扇形的半径为r,弧长为l,面积为S.
则l=20-2r,∴S=lr=(20-2r)·r=-r2+10r=+25(0<r<10).
∴当半径r=5 cm时,扇形的面积最大,为25 cm2.
此时α===2 rad.
∴当它的半径为5 cm,圆心角为2 rad时,扇形面积最大,最大值为25 cm2.
C
2.已知扇形周长为6cm,面积为2cm2,则扇形圆心角的弧度数为( )
A.1 B.4 C.1或4 D.2或4
C
D
1. 什么是角度制,什么是弧度制?怎么进行角度与弧度的互化?
2. 扇形的弧长及面积的计算公式.
7.1.2 弧度制及其与角度制的换算
人教B版(2019)必修第三册
1.了解弧度制,能熟练地进行弧度制与角度制之间的换算.
2.掌握弧度制中扇形的弧长公式和面积公式.
如图是一种折叠扇.折叠扇打开、合拢的过程 可以抽象成扇形圆心角的变大、变小.那么在这个过程中,扇形的什么量在发生变化?什么量没发生变化?由此你能想到度量角的其他办法吗?
变化的量:弧长、圆心角;
没有变化的量:半径.
问题:是否可以用弧长来度量圆心角呢?
60°的圆心角,半径r为1,2,3,分别计算对应的弧长l,再计算弧长与半径的比.
猜想:圆心角不变,则弧长与半径的比值不变.
问题一般化
问题1:观察下面两图,弧AB与弧A'B'都与什么有关?
将折叠扇抽象为如图所示的图形,可以看成弧AB与弧A'B'都与角α对应,但α≠0时,它们的弧长 与 始终不相等,其原因在于OA≠OA'.
问题一般化
问题2:那弧长与半径的比值有什么关系呢?
事实上,设α=n°,弧AB的长为l,半径OA=r,则 ,
因此 .
这个等式右边不包含半径,这表示弧长比半径的值不依赖于半径,而只与α的大小有关.
1.弧度数定义:弧长与半径比值的这个常数为圆心角的弧度数.
2.1弧度的角:长度等于半径长的圆弧所对的圆心角为1弧度的角, 记作1 rad.
以弧度为单位来度量角的制度称为弧度制.
如图,因为 的长度等于r,所以 所对的圆心角∠AOB就是1弧度的角.
问题3:通过对比角度制与弧度制的区别与联系,完成下列表格.
弧度制 角度制
区别
联系 无论弧度制还是角度制,
角的大小都是一个与半径大小无关的定值
弧度制以线段长度来度量角
角度制是“以角量角”
弧度制是十进制
角度制是六十进制
1弧度是等于半径长的弧
所对的圆心角的大小
1°的角是周角的
问题4:按照定义,一个周角对应的弧度数应是多少?
弧度与角度如何互化呢?
答:因为半径为r的圆周长为2πr,所以圆周的弧度数是 ,
于是360°=2π rad.
180°=π rad
角度与弧度的互化
思考:某同学表示与30°角终边相同的角的集合时写成S={α|α=2kπ+30°,k∈Z},这种表示正确吗?为什么?
这种表示不正确,同一个式子中,角度、弧度不能混用,否则产生混乱,
正确的表示方法应为{α|α=2kπ+,k∈Z}或{α|α=k·360°+30°,k∈Z}.
例1 用弧度表示终边落在阴影部分内(不包括边界)的角的集合.
解:330°角的终边与-30°角的终边相同,将-30°化为弧度,即-,
而75°=75×=,
所以终边落在阴影部分内(不包括边界)的角的集合为
{θ|2kπ-<θ<2kπ+,k∈Z}.
归纳总结
1.终边相同的角
若α与β的终边相同,则β=2kπ+ α(k∈Z),前后单位要一致.
2.象限角
第一象限角的集合:{α|2kπ<α<2kπ+,k∈Z};
第二象限角的集合:{α|2kπ+<α<2kπ+π,k∈Z};
第三象限角的集合:{α|2kπ+π<α<2kπ+, k∈Z};
第四象限角的集合:{α|2kπ+<α<2kπ+2π, k∈Z}.
常用角的弧度数表示
一些特殊角与弧度数的对应关系
角度 0° 15° 30° 45° 60° 75° 90° 120° 135° 150°
弧度
角度 180° 210° 225° 240° 270° 300° 315° 330° 360°
弧度
0
π
2π
例2 设角α1=-570°,α2=750°,β1=,β2=-.
(1)将α1,α2用弧度制表示出来,并指出它们各自所在的象限;
(2)将β1,β2用角度制表示出来,并在-720°~0°之间找出与它们终边相同的所有角.
解:(1)要确定角α所在的象限,只要把α表示为α=2kπ+α0(k∈Z,0≤α0<2π)的形式,由α0所在象限即可判定出α所在的象限.
α1=-570°=-=-4π+,
α2=750°==4π+.
∴α1在第二象限,α2在第一象限.
(2)β1==108°,设θ=β1+k·360°(k∈Z),
由-720°≤θ<0°,得-720°≤108°+k·360°<0°,
∴k=-2或k=-1,
∴在-720°~0°间与β1有相同终边的角是-612°和-252°.
同理β2=-420°且在-720°~0°间与β2有相同终边的角是-60°.
例2 设角α1=-570°,α2=750°,β1=,β2=-.
(2)将β1,β2用角度制表示出来,并在-720°~0°之间找出与它们终边相同的所有角.
角度制 弧度制
弧长公式
扇形面积公式
l =
S = lR =
l = |α|·R
S = lR = ·|α|·R2
若用 R 表示圆的半径,n( 0<n<360° ),α(0<α<2π)为圆心角,l 是扇形弧长,S 是扇形面积;结合前面所学,完成下面的表格:
思考:1.用公式|α|=求圆心角时,应注意什么问题?
2.在使用弧度制下的弧长公式及面积公式时,若已知的角是以“度”为单位,需注意什么问题?
1.应注意结果是圆心角的绝对值,具体应用时既要注意其大小,又要注意其正负.
2.若已知的角是以“度”为单位,则必须先把它化成弧度后再计算,否则结果出错.
例3 设扇形的周长为8 cm,面积为4 cm2,则扇形的圆心角的弧度数是( )
A.1 rad B.2 rad
C.3 rad D.4 rad
分析 设扇形半径为r,弧长为l,由题意得解得
则圆心角α==2 rad.
B
例4 已知扇形的周长为20 cm,当它的半径和圆心角各取什么值时,才能使扇形的面积最大?最大面积是多少?
解:设扇形的半径为r,弧长为l,面积为S.
则l=20-2r,∴S=lr=(20-2r)·r=-r2+10r=+25(0<r<10).
∴当半径r=5 cm时,扇形的面积最大,为25 cm2.
此时α===2 rad.
∴当它的半径为5 cm,圆心角为2 rad时,扇形面积最大,最大值为25 cm2.
C
2.已知扇形周长为6cm,面积为2cm2,则扇形圆心角的弧度数为( )
A.1 B.4 C.1或4 D.2或4
C
D
1. 什么是角度制,什么是弧度制?怎么进行角度与弧度的互化?
2. 扇形的弧长及面积的计算公式.
