3.1.1 基本计数原理 课件(共19张PPT) 2024-2025学年人教B版(2019)高中数学选择性必修第二册
文档属性
| 名称 | 3.1.1 基本计数原理 课件(共19张PPT) 2024-2025学年人教B版(2019)高中数学选择性必修第二册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 814.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教B版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-01-22 00:00:00 | ||
图片预览





文档简介
(共19张PPT)
3.1.1 基本计数原理
第三章 排列、组合与二项式定理
1.了解分类加法计数原理、分步乘法计数原理及其意义;
2.正确理解“完成一件事”的含义,能根据具体问题的特征,选择“分类”或“分步”;
3.能利用两个原理解决一些简单的实际问题.
小明忘记了由4个数字组成的手机锁屏密码,他最多要试多少次才能打开密码锁?
问题1:用一个大写的英文字母或一个阿拉伯数字给教室里的座位编号,总共能编出多少种不同的号码?
因为英文字母共有26个,阿拉伯数字共有10个,
所以总共可以编出26+10=36(种)不同的号码.
问题中最重要的特征是什么?
最重要的特征是“或”字的出现:每个座位都可以用一个英文字母或一个阿拉伯数字编号,有两类方案.
完成一件事有n类不同方案,在第1类方案中有m1种不同的方法,在第2类方案中有m2种不同的方法……在第n类方案中有mn种不同的方法.那么完成这件事共有种不同的方法.
分类加法计数原理
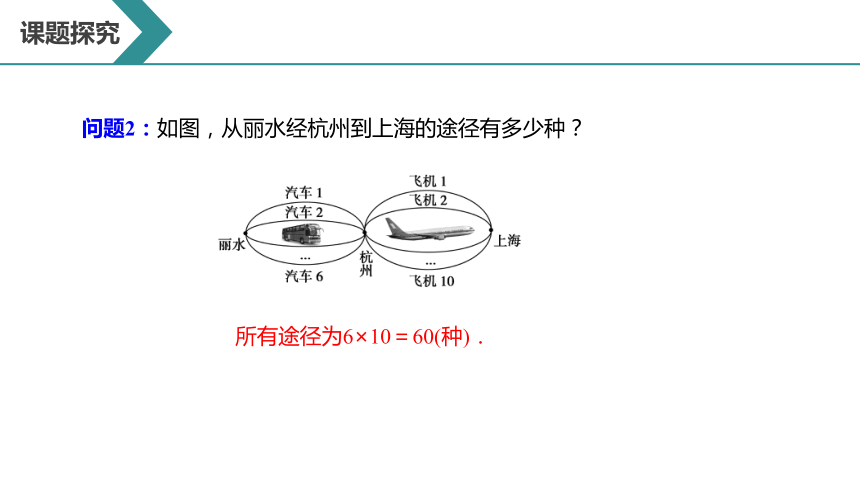
问题2:如图,从丽水经杭州到上海的途径有多少种?
所有途径为6×10=60(种).
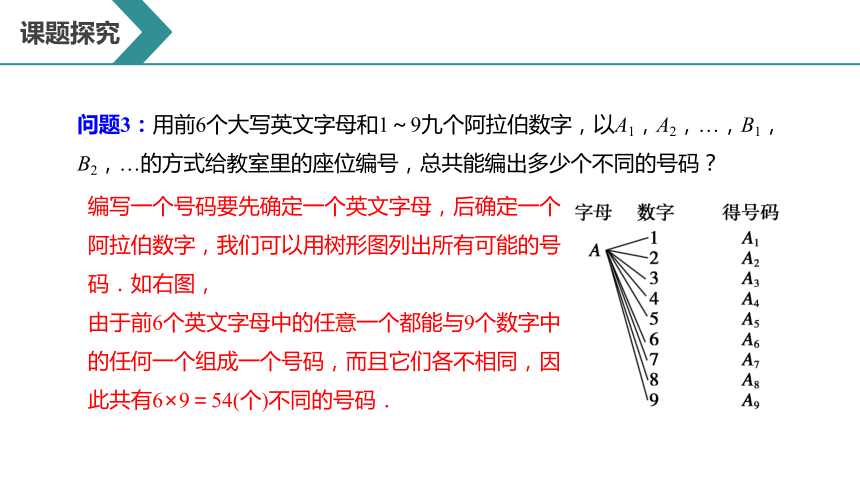
问题3:用前6个大写英文字母和1~9九个阿拉伯数字,以A1,A2,…,B1,
B2,…的方式给教室里的座位编号,总共能编出多少个不同的号码?
编写一个号码要先确定一个英文字母,后确定一个阿拉伯数字,我们可以用树形图列出所有可能的号码.如右图,
由于前6个英文字母中的任意一个都能与9个数字中的任何一个组成一个号码,而且它们各不相同,因此共有6×9=54(个)不同的号码.
分步乘法计数原理
完成一件事需要n个步骤,做第1步有m1种不同的方法,做第2步有m2种不同的方法……做第n步有mn种不同的方法,那么完成这件事共有种不同的方法.
讨论:完成一件事时,如何区分是分类还是分步
“分类”与“分步”的区别:①“分类”中,每种方法都能完成这件事,而“分步”中,每一步得到的只能是中间结果,缺少任何一个步骤都不能完成这件事.
②“分类”中,各个类别之间是独立的,而“分步”中,各步之间是关联的.
例1 我国古代十进制数的算筹记数法是世界数学史上一个伟大的创造.算筹一般为小圆棍,算筹计数法的表示方法为:个位用纵式,十位用横式,百位再用纵式,千位再用横式,以此类推;遇零则置空.纵式和横式对应数字的算筹表示如下表所示,例如:62记为“ ”.现用4根算筹表示一个两位数,则表示的数字为质数的个数为 .
4
数字 1 2 3 4 5 6 7 8 9
纵式 ____ _____ ______ ________ _________ _________ _________ _________ __________
横式 ____ ________ _________ _________ _________ __________ _________ __________ __________
解析:当十位用1根,个位用3根时,共有2个两位数13,17;
当十位用2根,个位用2根时,共有4个两位数22,26,62,66;
当十位用3根,个位用1根时,共有2个两位数31,71;
当十位用4根,个位用0根时,共有2个两位数40,80.
其中质数有13,17,31,71,所以表示的数字为质数的个数为4.
数字 1 2 3 4 5 6 7 8 9
纵式 ____ _____ ______ ________ _________ _________ _________ _________ __________
横式 ____ ________ _________ _________ _________ __________ _________ __________ __________
利用分类加法计数原理解题的一般思路:
(1)分类:将完成这件事的办法分成若干类;
(2)计数:求出每一类中的方法数;
(3)结论:将每一类中的方法数相加得最终结果.
归纳总结
例2 星期二下午的3节课排物理、化学和自习各一节,要求第一节不排自习,那么不同的排课方法的种数为 .(用数字作答)
解析:可以分为三步:第一步,排第一节课,有2种方法;
第二步,排第二节课,有2种方法;
第三步,排第三节课,只有1种方法,
故不同的排课方法的种数为 .
4
利用分步乘法计数原理解题的一般思路:
(1)分步:将完成这件事的过程分成若干步;
(2)计数:求出每一步中的方法数;
(3)结论:将每一步中的方法数相乘得最终结果
归纳总结
例3 在7名学生中,有3名会下象棋但不会下围棋,有2名会下围棋但不会下象棋,另2名既会下象棋又会下围棋.现在从这7人中选2人分别参加象棋比赛和围棋比赛,共有多少种不同的选法?
解:从3名只会下象棋的学生中选1名参加象棋比赛,同时从2名只会下围棋的学生中选1名参加围棋比赛有 (种)选法;
从3名只会下象棋的学生中选1名参加象棋比赛,同时从2名既会下象棋又会下围棋的学生中选1名参加围棋比赛有 (种)选法;
从2名只会下围棋的学生中选1名参加围棋比赛,同时从2名既会下象棋又会下围棋的学生中选1名参加象棋比赛有 (种)选法;
从2名既会下象棋又会下围棋的学生中选2名参加象棋比赛和围棋比赛有2种选法.
综上,共有 (种)选法.
例3 在7名学生中,有3名会下象棋但不会下围棋,有2名会下围棋但不会下象棋,另2名既会下象棋又会下围棋.现在从这7人中选2人分别参加象棋比赛和围棋比赛,共有多少种不同的选法?
根据下列关键词,构建知识导图.
“分类加法计数原理”、“分步乘法计数原理”
1.某班有男生26人,女生24人,从中选1人担任数学课代表,则不同的选法种数为( )
A.50 B.26 C.24 D.616
2.由0,1,2三个数字组成的三位数(允许数字重复)的个数为( )
A.27 B.18 C.12 D.6
A
B
3.已知集合,,, ,5,6, ,从两个集合中各取一个元素作为点的坐标,则这样的坐标在平面直角坐标系中表示第二象限内不同的点的个数为( )
A.2 B.4 C.5 D.6
4.如图所示的电路图,从A到B共有 条
不同的线路可通电.
D
8
3.1.1 基本计数原理
第三章 排列、组合与二项式定理
1.了解分类加法计数原理、分步乘法计数原理及其意义;
2.正确理解“完成一件事”的含义,能根据具体问题的特征,选择“分类”或“分步”;
3.能利用两个原理解决一些简单的实际问题.
小明忘记了由4个数字组成的手机锁屏密码,他最多要试多少次才能打开密码锁?
问题1:用一个大写的英文字母或一个阿拉伯数字给教室里的座位编号,总共能编出多少种不同的号码?
因为英文字母共有26个,阿拉伯数字共有10个,
所以总共可以编出26+10=36(种)不同的号码.
问题中最重要的特征是什么?
最重要的特征是“或”字的出现:每个座位都可以用一个英文字母或一个阿拉伯数字编号,有两类方案.
完成一件事有n类不同方案,在第1类方案中有m1种不同的方法,在第2类方案中有m2种不同的方法……在第n类方案中有mn种不同的方法.那么完成这件事共有种不同的方法.
分类加法计数原理
问题2:如图,从丽水经杭州到上海的途径有多少种?
所有途径为6×10=60(种).
问题3:用前6个大写英文字母和1~9九个阿拉伯数字,以A1,A2,…,B1,
B2,…的方式给教室里的座位编号,总共能编出多少个不同的号码?
编写一个号码要先确定一个英文字母,后确定一个阿拉伯数字,我们可以用树形图列出所有可能的号码.如右图,
由于前6个英文字母中的任意一个都能与9个数字中的任何一个组成一个号码,而且它们各不相同,因此共有6×9=54(个)不同的号码.
分步乘法计数原理
完成一件事需要n个步骤,做第1步有m1种不同的方法,做第2步有m2种不同的方法……做第n步有mn种不同的方法,那么完成这件事共有种不同的方法.
讨论:完成一件事时,如何区分是分类还是分步
“分类”与“分步”的区别:①“分类”中,每种方法都能完成这件事,而“分步”中,每一步得到的只能是中间结果,缺少任何一个步骤都不能完成这件事.
②“分类”中,各个类别之间是独立的,而“分步”中,各步之间是关联的.
例1 我国古代十进制数的算筹记数法是世界数学史上一个伟大的创造.算筹一般为小圆棍,算筹计数法的表示方法为:个位用纵式,十位用横式,百位再用纵式,千位再用横式,以此类推;遇零则置空.纵式和横式对应数字的算筹表示如下表所示,例如:62记为“ ”.现用4根算筹表示一个两位数,则表示的数字为质数的个数为 .
4
数字 1 2 3 4 5 6 7 8 9
纵式 ____ _____ ______ ________ _________ _________ _________ _________ __________
横式 ____ ________ _________ _________ _________ __________ _________ __________ __________
解析:当十位用1根,个位用3根时,共有2个两位数13,17;
当十位用2根,个位用2根时,共有4个两位数22,26,62,66;
当十位用3根,个位用1根时,共有2个两位数31,71;
当十位用4根,个位用0根时,共有2个两位数40,80.
其中质数有13,17,31,71,所以表示的数字为质数的个数为4.
数字 1 2 3 4 5 6 7 8 9
纵式 ____ _____ ______ ________ _________ _________ _________ _________ __________
横式 ____ ________ _________ _________ _________ __________ _________ __________ __________
利用分类加法计数原理解题的一般思路:
(1)分类:将完成这件事的办法分成若干类;
(2)计数:求出每一类中的方法数;
(3)结论:将每一类中的方法数相加得最终结果.
归纳总结
例2 星期二下午的3节课排物理、化学和自习各一节,要求第一节不排自习,那么不同的排课方法的种数为 .(用数字作答)
解析:可以分为三步:第一步,排第一节课,有2种方法;
第二步,排第二节课,有2种方法;
第三步,排第三节课,只有1种方法,
故不同的排课方法的种数为 .
4
利用分步乘法计数原理解题的一般思路:
(1)分步:将完成这件事的过程分成若干步;
(2)计数:求出每一步中的方法数;
(3)结论:将每一步中的方法数相乘得最终结果
归纳总结
例3 在7名学生中,有3名会下象棋但不会下围棋,有2名会下围棋但不会下象棋,另2名既会下象棋又会下围棋.现在从这7人中选2人分别参加象棋比赛和围棋比赛,共有多少种不同的选法?
解:从3名只会下象棋的学生中选1名参加象棋比赛,同时从2名只会下围棋的学生中选1名参加围棋比赛有 (种)选法;
从3名只会下象棋的学生中选1名参加象棋比赛,同时从2名既会下象棋又会下围棋的学生中选1名参加围棋比赛有 (种)选法;
从2名只会下围棋的学生中选1名参加围棋比赛,同时从2名既会下象棋又会下围棋的学生中选1名参加象棋比赛有 (种)选法;
从2名既会下象棋又会下围棋的学生中选2名参加象棋比赛和围棋比赛有2种选法.
综上,共有 (种)选法.
例3 在7名学生中,有3名会下象棋但不会下围棋,有2名会下围棋但不会下象棋,另2名既会下象棋又会下围棋.现在从这7人中选2人分别参加象棋比赛和围棋比赛,共有多少种不同的选法?
根据下列关键词,构建知识导图.
“分类加法计数原理”、“分步乘法计数原理”
1.某班有男生26人,女生24人,从中选1人担任数学课代表,则不同的选法种数为( )
A.50 B.26 C.24 D.616
2.由0,1,2三个数字组成的三位数(允许数字重复)的个数为( )
A.27 B.18 C.12 D.6
A
B
3.已知集合,,, ,5,6, ,从两个集合中各取一个元素作为点的坐标,则这样的坐标在平面直角坐标系中表示第二象限内不同的点的个数为( )
A.2 B.4 C.5 D.6
4.如图所示的电路图,从A到B共有 条
不同的线路可通电.
D
8
