4.2.2 离散型随机变量的分布列 课件(共20张PPT) 2024-2025学年人教B版(2019)高中数学选择性必修第二册
文档属性
| 名称 | 4.2.2 离散型随机变量的分布列 课件(共20张PPT) 2024-2025学年人教B版(2019)高中数学选择性必修第二册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 901.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教B版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-01-22 07:13:32 | ||
图片预览






文档简介
(共20张PPT)
4.2.2 离散型随机变量的分布列
第四章 概率与统计
1.理解取有限值的离散型随机变量及其分布列的概念与性质;
2.会求某些简单的离散型随机变量的分布列;
3.理解两点分布,并能简单的运用.
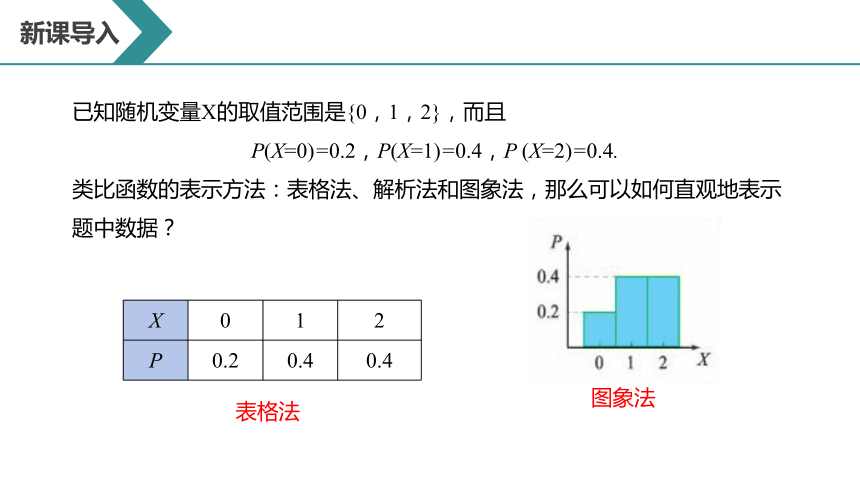
已知随机变量X的取值范围是{0,1,2},而且
P(X=0)=0.2,P(X=1)=0.4,P (X=2)=0.4.
类比函数的表示方法:表格法、解析法和图象法,那么可以如何直观地表示题中数据?
X 0 1 2
P 0.2 0.4 0.4
表格法
图象法
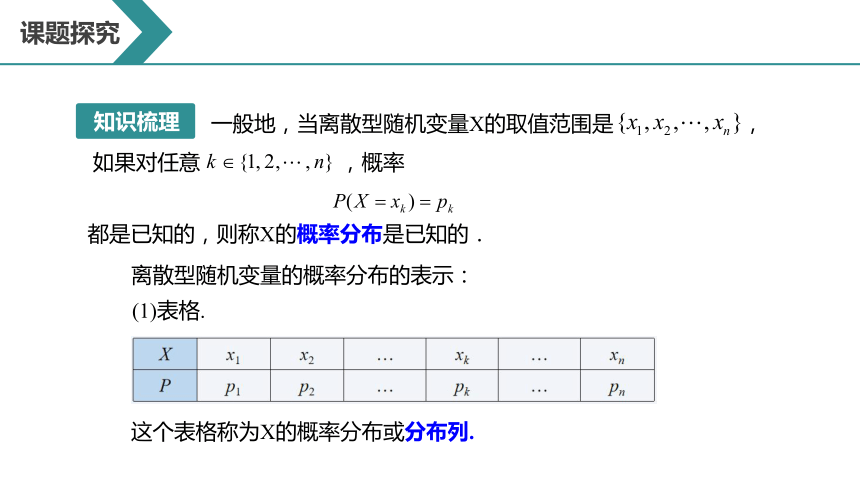
一般地,当离散型随机变量X的取值范围是 ,如果对任意 ,概率
都是已知的,则称X的概率分布是已知的.
(1)表格.
这个表格称为X的概率分布或分布列.
离散型随机变量的概率分布的表示:
知识梳理
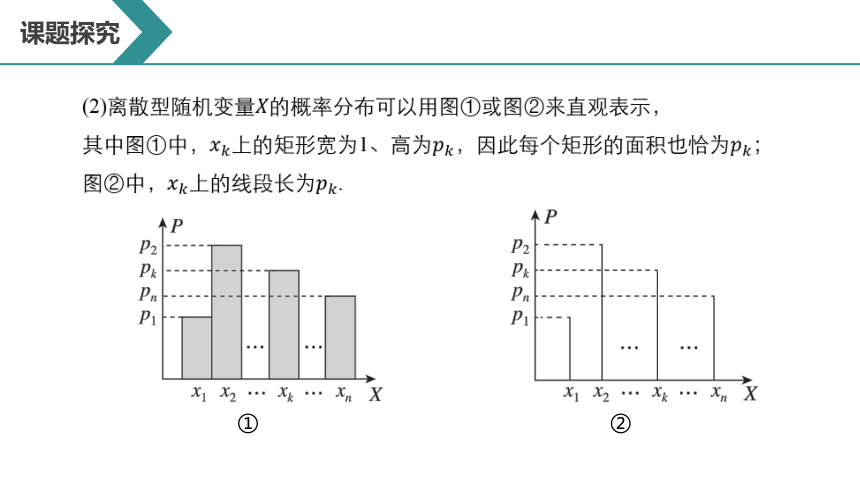
(2)离散型随机变量 的概率分布可以用图①或图②来直观表示,
其中图①中,上的矩形宽为1、高为,因此每个矩形的面积也恰为;图②中, 上的线段长为 .
①
②
抛掷一枚质地均匀的骰子,用X表示骰子向上一面的点数,则X的分布列为
问题:
(1)分布列中随机变量X取1,4,6时,对应的随机事件之间有什么关系?
(2)分布列中X分别取1,2,3,4,5,6时,它们的概率之和等于多少?
解:(1)X取1,4,6时,对应的随机事件是互斥的.
(2)概率之和为1.
离散型随机变量的分布列必须满足:
(1) ;
(2)
归纳总结
练习:设,随机变量 的分布列如下表所示,则 ( )
5 8 9
D
A. B. C. D.
对阵球员
例1 , 两个乒乓球队进行对抗赛,每队出三名队员,队队员为,,,队队员为,, .按照以往比赛统计,对阵队员之间胜负的概率如下表:
现按表中对阵方式出场,每场获胜的队伍得1分,输的队伍得0分,设队, 队最后所得总分分别为与 ,求与 的分布列.
解:由题意可知的取值范围为,2,1,, ,
,
,
.
由题意可知,所以 的取值范围为,1,2, ,
, ,
, .
故与 的分布列分别为
3 2 1 0
0 1 2 3
求离散型随机变量的分布列的关键有三点:
(1)“判断取值”,即判断随机变量的所有可能取值以及取每个值所表示的意义;
(2)“探求概率”,即利用排列组合、枚举法、概率公式(常见的有古典概型概率公式、互斥事件的概率和公式、独立事件的概率公式以及对立事件的概率公式等)求出随机变量取每个值时的概率;
(3)“写分布列”,即按规范形式写出分布列,并注意用分布列的性质检验所求的分布列或事件的概率是否正确.
归纳总结
例2 某运动员射击命中10环的概率为 ,求该运动员在一次射击中命中10环的次数的分布列.
解:设该运动员在一次射击中命中10环的次数为 ,
则,,
故 的分布列为
0 1
0.1 0.9
X 1 0
P p 1-p
则称随机变量X 服从参数为p的两点分布(或0-1分布).
一般地,如果随机变量X的分布列能写成如下表格的形式:
两点分布
知识梳理
伯努利试验:一个所有可能结果只有两种的随机试验.
因此两点分布也常称为伯努利分布.
若伯努利试验结果看成“成功”(出现概率为p)与“不成功”,一次伯努利试验中“成功”出现的次数为X,则X服从参数为p的两点分布:
X 1 0
P p 1-p
例3 若离散型随机变量 的分布列如下表所示.
0 1
求出,并说明是否服从参数为 的两点分布,若是,则成功概率是多少
解:由,解得或 ,
又,,所以,则.
因为的取值范围为 ,所以服从参数为的两点分布,成功概率是 .
两步法判断一个分布是否为两点分布:
(1)看取值,随机变量只取两个值0和1.
(2)验概率,检验 是否成立.
如果一个分布满足以上两点,则该分布是两点分布,否则不是两点分布.
归纳总结
1.已知随机变量的分布列如下表,则 ( )
A
1 2 3
0.25
A.0.75 B.1.5 C.1 D.0.25
2.设随机变量服从参数为的两点分布,若,
则 ( )
A.0.2 B.0.4 C.0.6 D.0.8
C
3.设离散型随机变量X的分布列为
A
X 0 1 2 3 4
P 0.2 0.1 0.1 0.3 m
若随机变量Y=X-2,则P(Y=2)等于( )
A.0.3 B.0.4 C.0.6 D.0.7
4.2.2 离散型随机变量的分布列
第四章 概率与统计
1.理解取有限值的离散型随机变量及其分布列的概念与性质;
2.会求某些简单的离散型随机变量的分布列;
3.理解两点分布,并能简单的运用.
已知随机变量X的取值范围是{0,1,2},而且
P(X=0)=0.2,P(X=1)=0.4,P (X=2)=0.4.
类比函数的表示方法:表格法、解析法和图象法,那么可以如何直观地表示题中数据?
X 0 1 2
P 0.2 0.4 0.4
表格法
图象法
一般地,当离散型随机变量X的取值范围是 ,如果对任意 ,概率
都是已知的,则称X的概率分布是已知的.
(1)表格.
这个表格称为X的概率分布或分布列.
离散型随机变量的概率分布的表示:
知识梳理
(2)离散型随机变量 的概率分布可以用图①或图②来直观表示,
其中图①中,上的矩形宽为1、高为,因此每个矩形的面积也恰为;图②中, 上的线段长为 .
①
②
抛掷一枚质地均匀的骰子,用X表示骰子向上一面的点数,则X的分布列为
问题:
(1)分布列中随机变量X取1,4,6时,对应的随机事件之间有什么关系?
(2)分布列中X分别取1,2,3,4,5,6时,它们的概率之和等于多少?
解:(1)X取1,4,6时,对应的随机事件是互斥的.
(2)概率之和为1.
离散型随机变量的分布列必须满足:
(1) ;
(2)
归纳总结
练习:设,随机变量 的分布列如下表所示,则 ( )
5 8 9
D
A. B. C. D.
对阵球员
例1 , 两个乒乓球队进行对抗赛,每队出三名队员,队队员为,,,队队员为,, .按照以往比赛统计,对阵队员之间胜负的概率如下表:
现按表中对阵方式出场,每场获胜的队伍得1分,输的队伍得0分,设队, 队最后所得总分分别为与 ,求与 的分布列.
解:由题意可知的取值范围为,2,1,, ,
,
,
.
由题意可知,所以 的取值范围为,1,2, ,
, ,
, .
故与 的分布列分别为
3 2 1 0
0 1 2 3
求离散型随机变量的分布列的关键有三点:
(1)“判断取值”,即判断随机变量的所有可能取值以及取每个值所表示的意义;
(2)“探求概率”,即利用排列组合、枚举法、概率公式(常见的有古典概型概率公式、互斥事件的概率和公式、独立事件的概率公式以及对立事件的概率公式等)求出随机变量取每个值时的概率;
(3)“写分布列”,即按规范形式写出分布列,并注意用分布列的性质检验所求的分布列或事件的概率是否正确.
归纳总结
例2 某运动员射击命中10环的概率为 ,求该运动员在一次射击中命中10环的次数的分布列.
解:设该运动员在一次射击中命中10环的次数为 ,
则,,
故 的分布列为
0 1
0.1 0.9
X 1 0
P p 1-p
则称随机变量X 服从参数为p的两点分布(或0-1分布).
一般地,如果随机变量X的分布列能写成如下表格的形式:
两点分布
知识梳理
伯努利试验:一个所有可能结果只有两种的随机试验.
因此两点分布也常称为伯努利分布.
若伯努利试验结果看成“成功”(出现概率为p)与“不成功”,一次伯努利试验中“成功”出现的次数为X,则X服从参数为p的两点分布:
X 1 0
P p 1-p
例3 若离散型随机变量 的分布列如下表所示.
0 1
求出,并说明是否服从参数为 的两点分布,若是,则成功概率是多少
解:由,解得或 ,
又,,所以,则.
因为的取值范围为 ,所以服从参数为的两点分布,成功概率是 .
两步法判断一个分布是否为两点分布:
(1)看取值,随机变量只取两个值0和1.
(2)验概率,检验 是否成立.
如果一个分布满足以上两点,则该分布是两点分布,否则不是两点分布.
归纳总结
1.已知随机变量的分布列如下表,则 ( )
A
1 2 3
0.25
A.0.75 B.1.5 C.1 D.0.25
2.设随机变量服从参数为的两点分布,若,
则 ( )
A.0.2 B.0.4 C.0.6 D.0.8
C
3.设离散型随机变量X的分布列为
A
X 0 1 2 3 4
P 0.2 0.1 0.1 0.3 m
若随机变量Y=X-2,则P(Y=2)等于( )
A.0.3 B.0.4 C.0.6 D.0.7
