人教版数学八年级下册18.2.2 菱形的性质(含解析)
文档属性
| 名称 | 人教版数学八年级下册18.2.2 菱形的性质(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 784.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-01-24 12:28:47 | ||
图片预览



文档简介
18.2.2 菱形的性质
一、单选题:
1.矩形具有而菱形不一定具有的性质是( )
A.对边分别相等 B.对角分别相等 C.对角线互相平分 D.对角线相等
2.菱形的两条对角线的长分别是和,则菱形的面积是( )
A. B. C. D.
3.已知菱形,,,则菱形的面积为( )
A. B. C. D.
4.菱形的周长为,两个相邻的内角度数之比为,则较短的对角线长度是( )
A. B. C. D.
5.如图,菱形的边长为2,,则点A的坐标为( )
A. B. C. D.
6.如图,菱形的对角线相交于点O,过点A作于点E,连接.若,菱形的面积为54,则的长为( )
A.4 B.4.5 C.5 D.5.5
7.如图,在菱形ABCD中,对角线AC与BD.相交于点O,OE⊥AB,垂足为E,若∠ADC=130°,则∠AOE的大小为( )
A.21 B.65 C.42 D.56
8.如图,菱形的周长为,对角线、相交于点O,,垂足为E,,则为( )
A. B. C. D.4cm
二、填空题:
9.如图,菱形ABCD中,EF是AB的垂直平分线,∠FBA=50°,则∠ACB=_____.
10.如图,在荾形中,对角线,分别为和,于点,则______.
11.如图,菱形的对角线相交于点O,过点D作于点H,连接,若,则菱形的面积为_______.
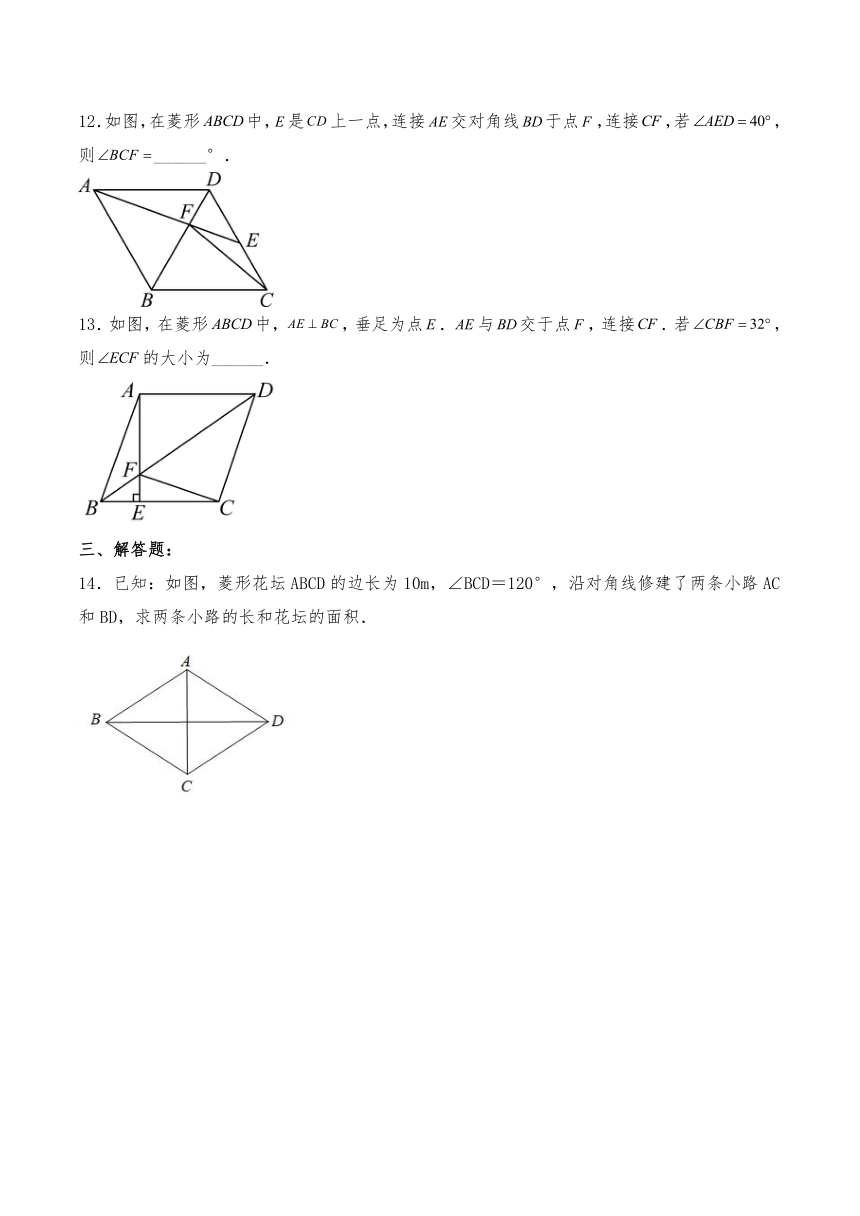
12.如图,在菱形中,是上一点,连接交对角线于点,连接,若,则______°.
13.如图,在菱形中,,垂足为点.与交于点,连接.若,则的大小为______.
三、解答题:
14.已知:如图,菱形花坛ABCD的边长为10m,∠BCD=120°,沿对角线修建了两条小路AC和BD,求两条小路的长和花坛的面积.
15.如图,菱形的对角线相交于点O,垂直平分,垂足为点E,求的大小.
16.如图,菱形,、分别是,上的点,,,求的度数.
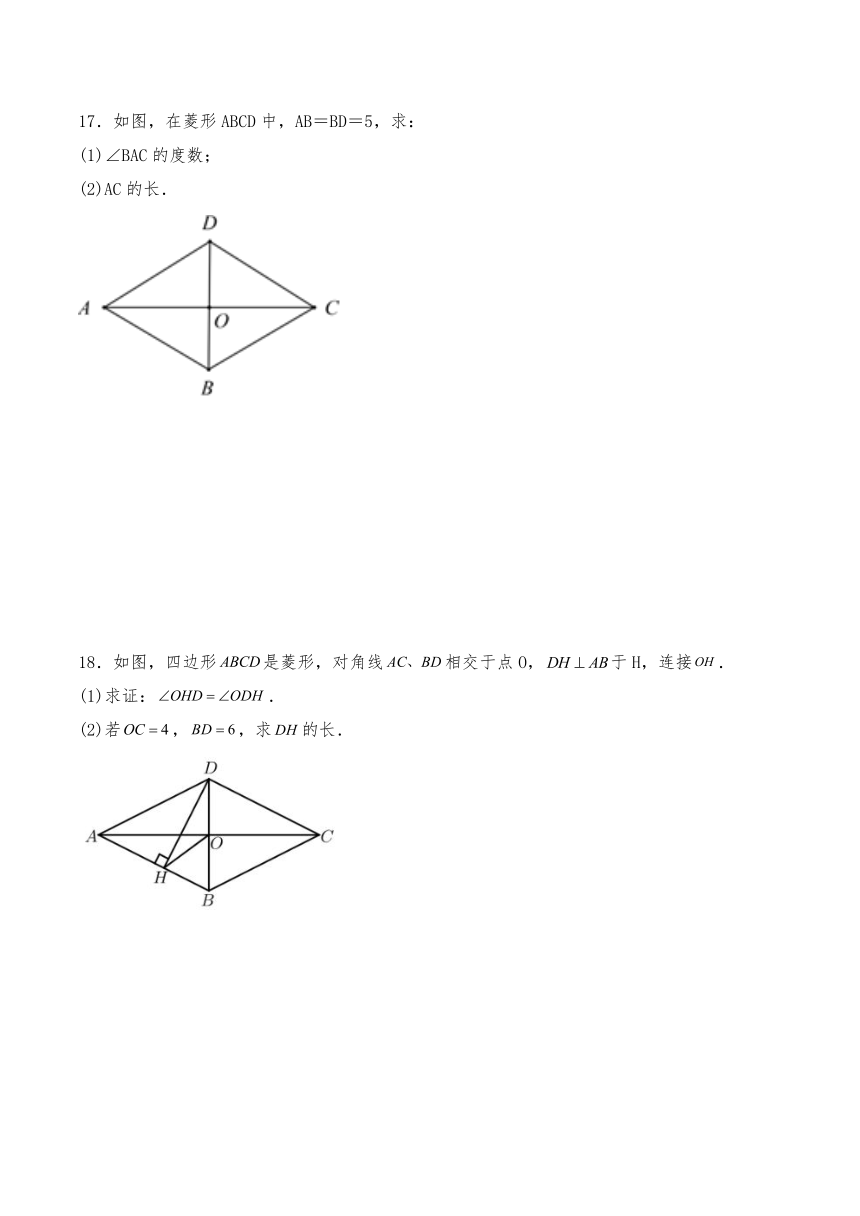
17.如图,在菱形ABCD中,AB=BD=5,求:
(1)∠BAC的度数;
(2)AC的长.
18.如图,四边形是菱形,对角线相交于点O,于H,连接.
(1)求证:.
(2)若,,求的长.
19.如图,已知菱形的顶点,的坐标分别为,,点在轴上.
(1)求点的坐标;
(2)如图,对角线,相交于点,求,的长及点的坐标.
20.在菱形中,,是对角线上任意一点,是线段延长线上一点,且,连接、.
(1)如图1,当是线段的中点时,和的数量关系是__________.
(2)如图2,当点不是线段的中点,其它条件不变时,请你判断(1)中的结论是否成立?若成立,请给予证明;若不成立,请说明理由.
答案
一、单选题:
1.D
【分析】根据矩形和菱形的性质进行判断即可得出答案.
【详解】解:矩形具有而菱形不一定具有的性质是对角线相等,
故选:D.
2.A
【分析】根据菱形的面积公式即可求解.
【详解】∵菱形的两条对角线的长分别为和,
∴面积为
故选:A.
3.D
【分析】过点作于点,根据题意求得,进而可得,勾股定理求得,根据菱形的面积公式进行计算即可求解.
【详解】解:如图,过点作于点,
∵四边形是菱形,
∴,
,
∴,则,
∴,
∴菱形的面积为(cm2).
故选D.
4.A
【分析】根据菱形的对角线互相垂直且平分各角,可设较小角为x,因为邻角之和为180°,所以x+2x=180°,所以x=60°,画出其图形,根据含30度角的直角三角形的性质,可以得到其中较短的对角线的长.
【详解】解:如图所示:
∵菱形的周长为24cm,
∴菱形的边长为6cm,AC⊥BD,∠ABC+∠BCD=180°,
∵两邻角之比为1:2,
∴较小角60°,
∴∠ABO=30°,AB=6cm,
∴最短边为AC,AO=AB=3cm,
∴AC=2AO=6cm.
故选:A.
5.D
【分析】根据坐标意义,点A坐标与垂线段有关,过点A向x轴垂线段AE,求得OE、AE的长即可知点A坐标.
【详解】过点A作AE⊥x轴,垂足为E,则∠AEO=90°,
∵,∠AEO=90°
∴,
∴
∵菱形的边长为2即AO=2,∠AEO=90°,
∴,即
解得:.
∴点A坐标为,
故选:D.
6.B
【分析】由菱形的性质可得,由菱形的面积得可得,然后根据直角三角形斜边上的中线性质即可解答.
【详解】解:∵四边形是菱形,
∴,
∴,
∵,
∴,
∵,
∴,
∴.
故选:B.
7.B
【分析】根据“菱形的性质、三角形内角和定理”结合已知条件分析解答即可.
【详解】解:在菱形ABCD中,∠ADC=130°,
∴∠BAD=180°﹣130°=50°,
∴∠BAO=∠BAD=×50°=25°,
∵OE⊥AB,
∴∠AOE=90°﹣∠BAO=90°﹣25°=65°.
故选:B.
8.B
【分析】根据菱形的性质和周长,求出边长,利用勾股定理,分别求出利用等积法求出即可.
【详解】解:∵菱形的周长为,
∴,
∵,垂足为E,,
∴,
∴,
∴,
∵,即:,
∴;
故选B.
二、填空题:
9.25°
【分析】由线段垂直平分线的性质可得AF=BF,由等腰三角形的性质可得∠FAB=∠FBA=50°,由菱形的性质可得∠BAC=∠BAD=25°,AB=BC,即可求解.
【详解】解:∵EF是AB的垂直平分线,
∴AF=BF,
∴∠FAB=∠FBA=50°,
∵四边形ABCD是菱形,
∴∠BAC=∠BAD=25°,AB=BC,
∴∠BAC=∠ACB=25°,
故答案为:25°.
10.
【分析】由菱形的性质可得,,,由勾股定理可求的长,由菱形的面积公式可求解.
【详解】解:如图,设与的交点为O,
∵四边形是菱形,
,,,
,
,
,
,
故答案为:.
11.48
【分析】由菱形的性质得,,,则,再由直角三角形斜边上的中线性质求出的长度,然后由菱形的面积公式求解即可.
【详解】解:∵四边形是菱形,
∴,,,
∴,
∵,
∴,
∴,
∴菱形的面积,
故答案为:48.
12.40
【分析】由“SAS”可证△ABF≌△CBF,可得∠BAF=∠BCF,由平行线的性质可求解.
【详解】解:∵四边形ABCD是菱形,
∴AB=CB,AB∥DC,∠ABF=∠CBF,
∵AB=CB,∠ABF=∠CBF,BF=BF,
∴△ABF≌△CBF(SAS),
∴∠BAF=∠BCF,
∵∠AED=40°,AD∥BC,
∴∠AED=∠BAF,
∴∠BCF=40°,
故答案为:40.
13.
【分析】根据菱形的性质,得出,,再根据,得出,再根据全等三角形的性质,得出,再根据菱形的性质,得出,再根据垂线的定义,得出,再根据三角形的内角和定理,得出,进而即可得出结果.
【详解】解:∵四边形是菱形,
∴,,
在和中,
,
∴,
∴,
∵,
∵,
∴,
∴,
∴,
即.
故答案为:
三、解答题:
14.解:∵菱形花坛ABCD的边长为10m,∠BCD=120°,
∴AB=BC=DC=AD=10m,=,
∴△ABC是等边三角形,,
∴AC=10m,
设交于点,
∴AO=5m,
∴BO=(m),
则BD=10m,AC=10m;
花坛的面积为:×10×10()=(),
答:两条小路的长分别为10m,10m;花坛的面积为().
15.解:在菱形ABCD中,有,且,
∵DE垂直平分BC,
∴,
∴,
∴为等边三角形,
∴,
∵,
∴,
∴,
即∠ABC的度数为120°.
16.连接,
∵四边形是菱形,
∴为等边三角形,
∴,,
∴,
∵,
∴,
∴△ABE≌△ACF,
∴,
∴为等边三角形,
∴,
∵,且,
∴
17.
(1)
∵四边形ABCD为菱形,
∴AB=AD,AC平分∠BAD,
∵AB=BD=5,
∴AB=AD=BD,
∴△ABD为等边三角形,
∴∠BAD=60°,
∴∠BAC=30°;
(2)
∵四边形ABCD为菱形,
∴OA=OC,BO=OD=BD=,BD⊥AC,
在Rt△AOB中,OA=,
∴AC=2OA=.
18.(1)∵四边形是菱形,
∴,
∵,
∴,
∴,
∴;
(2)∵四边形是菱形,
∴,,,
∴,,
在中,,
∴
∴
∴
∴.
19.(1),的坐标分别为,,
,,
四边形是菱形,
∴,
在中,由勾股定理得,,
∴;
(2)在中,由勾股定理得,,
∵,
,
四边形是菱形,
∴G为AC的中点
.
20.(1)
∵四边形ABCD是菱形,
∴AB=BC.
∵∠ABC=60°,
∴△ABC是等边三角形,
∴∠BCA=60°.
∵E是线段AC的中点,
∴∠CBE=∠ABE=30°,AE=CE.
∵CF=AE,
∴CE=CF,
∴,
∴∠CBE=∠F=30°,
∴BE=EF.
故答案为:BE=EF;
(2)
结论成立,证明如下:
如图,过点E作EG∥BC交AB于点G,
∵四边形ABCD为菱形,
∴AB=BC,∠BCD=120°,AB∥CD,
∴∠ACD=60°,∠DCF=∠ABC=60°,
∴∠ECF=120°.
又∵∠ABC=60°,
∴△ABC是等边三角形,
∴AB=AC,∠ACB=60°.
又∵EG∥BC,
∴∠AGE=∠ABC=60°.
∵∠BAC=60°,
∴△AGE是等边三角形,
∴AG=AE=GE,∠AGE=60°,
∴BG=CE,∠BGE=120°=∠ECF.
又∵CF=AE,
∴GE=CF.
即在△BGE和△CEF中,,
∴△BGE≌△ECF(SAS),
∴BE=EF.
一、单选题:
1.矩形具有而菱形不一定具有的性质是( )
A.对边分别相等 B.对角分别相等 C.对角线互相平分 D.对角线相等
2.菱形的两条对角线的长分别是和,则菱形的面积是( )
A. B. C. D.
3.已知菱形,,,则菱形的面积为( )
A. B. C. D.
4.菱形的周长为,两个相邻的内角度数之比为,则较短的对角线长度是( )
A. B. C. D.
5.如图,菱形的边长为2,,则点A的坐标为( )
A. B. C. D.
6.如图,菱形的对角线相交于点O,过点A作于点E,连接.若,菱形的面积为54,则的长为( )
A.4 B.4.5 C.5 D.5.5
7.如图,在菱形ABCD中,对角线AC与BD.相交于点O,OE⊥AB,垂足为E,若∠ADC=130°,则∠AOE的大小为( )
A.21 B.65 C.42 D.56
8.如图,菱形的周长为,对角线、相交于点O,,垂足为E,,则为( )
A. B. C. D.4cm
二、填空题:
9.如图,菱形ABCD中,EF是AB的垂直平分线,∠FBA=50°,则∠ACB=_____.
10.如图,在荾形中,对角线,分别为和,于点,则______.
11.如图,菱形的对角线相交于点O,过点D作于点H,连接,若,则菱形的面积为_______.
12.如图,在菱形中,是上一点,连接交对角线于点,连接,若,则______°.
13.如图,在菱形中,,垂足为点.与交于点,连接.若,则的大小为______.
三、解答题:
14.已知:如图,菱形花坛ABCD的边长为10m,∠BCD=120°,沿对角线修建了两条小路AC和BD,求两条小路的长和花坛的面积.
15.如图,菱形的对角线相交于点O,垂直平分,垂足为点E,求的大小.
16.如图,菱形,、分别是,上的点,,,求的度数.
17.如图,在菱形ABCD中,AB=BD=5,求:
(1)∠BAC的度数;
(2)AC的长.
18.如图,四边形是菱形,对角线相交于点O,于H,连接.
(1)求证:.
(2)若,,求的长.
19.如图,已知菱形的顶点,的坐标分别为,,点在轴上.
(1)求点的坐标;
(2)如图,对角线,相交于点,求,的长及点的坐标.
20.在菱形中,,是对角线上任意一点,是线段延长线上一点,且,连接、.
(1)如图1,当是线段的中点时,和的数量关系是__________.
(2)如图2,当点不是线段的中点,其它条件不变时,请你判断(1)中的结论是否成立?若成立,请给予证明;若不成立,请说明理由.
答案
一、单选题:
1.D
【分析】根据矩形和菱形的性质进行判断即可得出答案.
【详解】解:矩形具有而菱形不一定具有的性质是对角线相等,
故选:D.
2.A
【分析】根据菱形的面积公式即可求解.
【详解】∵菱形的两条对角线的长分别为和,
∴面积为
故选:A.
3.D
【分析】过点作于点,根据题意求得,进而可得,勾股定理求得,根据菱形的面积公式进行计算即可求解.
【详解】解:如图,过点作于点,
∵四边形是菱形,
∴,
,
∴,则,
∴,
∴菱形的面积为(cm2).
故选D.
4.A
【分析】根据菱形的对角线互相垂直且平分各角,可设较小角为x,因为邻角之和为180°,所以x+2x=180°,所以x=60°,画出其图形,根据含30度角的直角三角形的性质,可以得到其中较短的对角线的长.
【详解】解:如图所示:
∵菱形的周长为24cm,
∴菱形的边长为6cm,AC⊥BD,∠ABC+∠BCD=180°,
∵两邻角之比为1:2,
∴较小角60°,
∴∠ABO=30°,AB=6cm,
∴最短边为AC,AO=AB=3cm,
∴AC=2AO=6cm.
故选:A.
5.D
【分析】根据坐标意义,点A坐标与垂线段有关,过点A向x轴垂线段AE,求得OE、AE的长即可知点A坐标.
【详解】过点A作AE⊥x轴,垂足为E,则∠AEO=90°,
∵,∠AEO=90°
∴,
∴
∵菱形的边长为2即AO=2,∠AEO=90°,
∴,即
解得:.
∴点A坐标为,
故选:D.
6.B
【分析】由菱形的性质可得,由菱形的面积得可得,然后根据直角三角形斜边上的中线性质即可解答.
【详解】解:∵四边形是菱形,
∴,
∴,
∵,
∴,
∵,
∴,
∴.
故选:B.
7.B
【分析】根据“菱形的性质、三角形内角和定理”结合已知条件分析解答即可.
【详解】解:在菱形ABCD中,∠ADC=130°,
∴∠BAD=180°﹣130°=50°,
∴∠BAO=∠BAD=×50°=25°,
∵OE⊥AB,
∴∠AOE=90°﹣∠BAO=90°﹣25°=65°.
故选:B.
8.B
【分析】根据菱形的性质和周长,求出边长,利用勾股定理,分别求出利用等积法求出即可.
【详解】解:∵菱形的周长为,
∴,
∵,垂足为E,,
∴,
∴,
∴,
∵,即:,
∴;
故选B.
二、填空题:
9.25°
【分析】由线段垂直平分线的性质可得AF=BF,由等腰三角形的性质可得∠FAB=∠FBA=50°,由菱形的性质可得∠BAC=∠BAD=25°,AB=BC,即可求解.
【详解】解:∵EF是AB的垂直平分线,
∴AF=BF,
∴∠FAB=∠FBA=50°,
∵四边形ABCD是菱形,
∴∠BAC=∠BAD=25°,AB=BC,
∴∠BAC=∠ACB=25°,
故答案为:25°.
10.
【分析】由菱形的性质可得,,,由勾股定理可求的长,由菱形的面积公式可求解.
【详解】解:如图,设与的交点为O,
∵四边形是菱形,
,,,
,
,
,
,
故答案为:.
11.48
【分析】由菱形的性质得,,,则,再由直角三角形斜边上的中线性质求出的长度,然后由菱形的面积公式求解即可.
【详解】解:∵四边形是菱形,
∴,,,
∴,
∵,
∴,
∴,
∴菱形的面积,
故答案为:48.
12.40
【分析】由“SAS”可证△ABF≌△CBF,可得∠BAF=∠BCF,由平行线的性质可求解.
【详解】解:∵四边形ABCD是菱形,
∴AB=CB,AB∥DC,∠ABF=∠CBF,
∵AB=CB,∠ABF=∠CBF,BF=BF,
∴△ABF≌△CBF(SAS),
∴∠BAF=∠BCF,
∵∠AED=40°,AD∥BC,
∴∠AED=∠BAF,
∴∠BCF=40°,
故答案为:40.
13.
【分析】根据菱形的性质,得出,,再根据,得出,再根据全等三角形的性质,得出,再根据菱形的性质,得出,再根据垂线的定义,得出,再根据三角形的内角和定理,得出,进而即可得出结果.
【详解】解:∵四边形是菱形,
∴,,
在和中,
,
∴,
∴,
∵,
∵,
∴,
∴,
∴,
即.
故答案为:
三、解答题:
14.解:∵菱形花坛ABCD的边长为10m,∠BCD=120°,
∴AB=BC=DC=AD=10m,=,
∴△ABC是等边三角形,,
∴AC=10m,
设交于点,
∴AO=5m,
∴BO=(m),
则BD=10m,AC=10m;
花坛的面积为:×10×10()=(),
答:两条小路的长分别为10m,10m;花坛的面积为().
15.解:在菱形ABCD中,有,且,
∵DE垂直平分BC,
∴,
∴,
∴为等边三角形,
∴,
∵,
∴,
∴,
即∠ABC的度数为120°.
16.连接,
∵四边形是菱形,
∴为等边三角形,
∴,,
∴,
∵,
∴,
∴△ABE≌△ACF,
∴,
∴为等边三角形,
∴,
∵,且,
∴
17.
(1)
∵四边形ABCD为菱形,
∴AB=AD,AC平分∠BAD,
∵AB=BD=5,
∴AB=AD=BD,
∴△ABD为等边三角形,
∴∠BAD=60°,
∴∠BAC=30°;
(2)
∵四边形ABCD为菱形,
∴OA=OC,BO=OD=BD=,BD⊥AC,
在Rt△AOB中,OA=,
∴AC=2OA=.
18.(1)∵四边形是菱形,
∴,
∵,
∴,
∴,
∴;
(2)∵四边形是菱形,
∴,,,
∴,,
在中,,
∴
∴
∴
∴.
19.(1),的坐标分别为,,
,,
四边形是菱形,
∴,
在中,由勾股定理得,,
∴;
(2)在中,由勾股定理得,,
∵,
,
四边形是菱形,
∴G为AC的中点
.
20.(1)
∵四边形ABCD是菱形,
∴AB=BC.
∵∠ABC=60°,
∴△ABC是等边三角形,
∴∠BCA=60°.
∵E是线段AC的中点,
∴∠CBE=∠ABE=30°,AE=CE.
∵CF=AE,
∴CE=CF,
∴,
∴∠CBE=∠F=30°,
∴BE=EF.
故答案为:BE=EF;
(2)
结论成立,证明如下:
如图,过点E作EG∥BC交AB于点G,
∵四边形ABCD为菱形,
∴AB=BC,∠BCD=120°,AB∥CD,
∴∠ACD=60°,∠DCF=∠ABC=60°,
∴∠ECF=120°.
又∵∠ABC=60°,
∴△ABC是等边三角形,
∴AB=AC,∠ACB=60°.
又∵EG∥BC,
∴∠AGE=∠ABC=60°.
∵∠BAC=60°,
∴△AGE是等边三角形,
∴AG=AE=GE,∠AGE=60°,
∴BG=CE,∠BGE=120°=∠ECF.
又∵CF=AE,
∴GE=CF.
即在△BGE和△CEF中,,
∴△BGE≌△ECF(SAS),
∴BE=EF.
