人教版数学八年级下册18.2.3 正方形(含解析)
文档属性
| 名称 | 人教版数学八年级下册18.2.3 正方形(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-01-24 12:30:35 | ||
图片预览

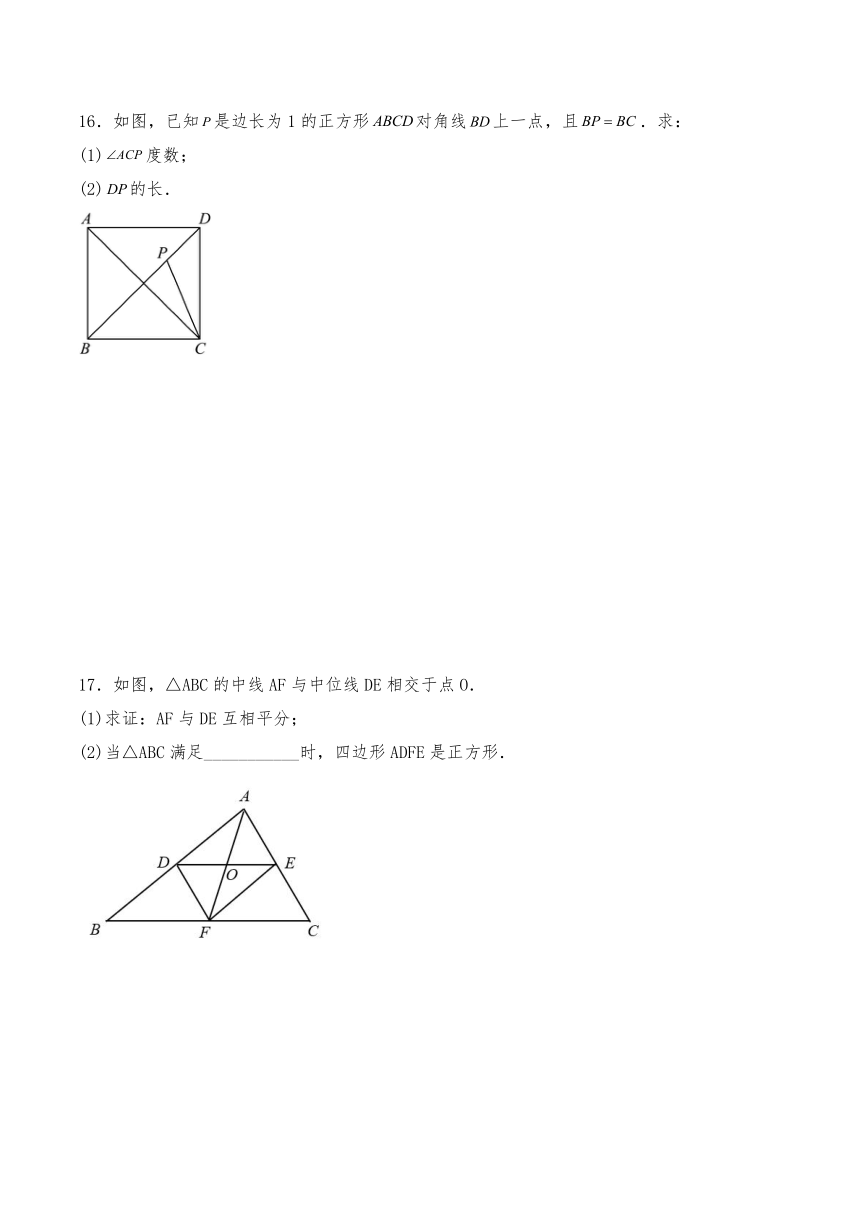
文档简介
18.2.3 正方形
一、单选题:
1.如图所示,顺次连接四边形各边中点得到四边形,使四边形为正方形,应添加的条件分别是( )
A.且 B.且
C.且 D.且
2.下列是关于某个四边形的三个结论:①它的对角线互相垂直;②它是一个正方形;③它是一个菱形.下列推理过程正确的是( )
A.由②推出③,由③推出① B.由①推出②,由②推出③
C.由③推出①,由①推出③ D.由①推出③,由③推出②
3.如图,在边长为5的正方形内作,交于点,交于点,连接,若,则的长为( )
A. B. C. D.2
4.如图,把正方形放在直角坐标系中,直角顶点落在第二象限,顶点、分别落在轴、轴上,已知点、,则点的坐标为( )
A.(-4,0) B. C. D.
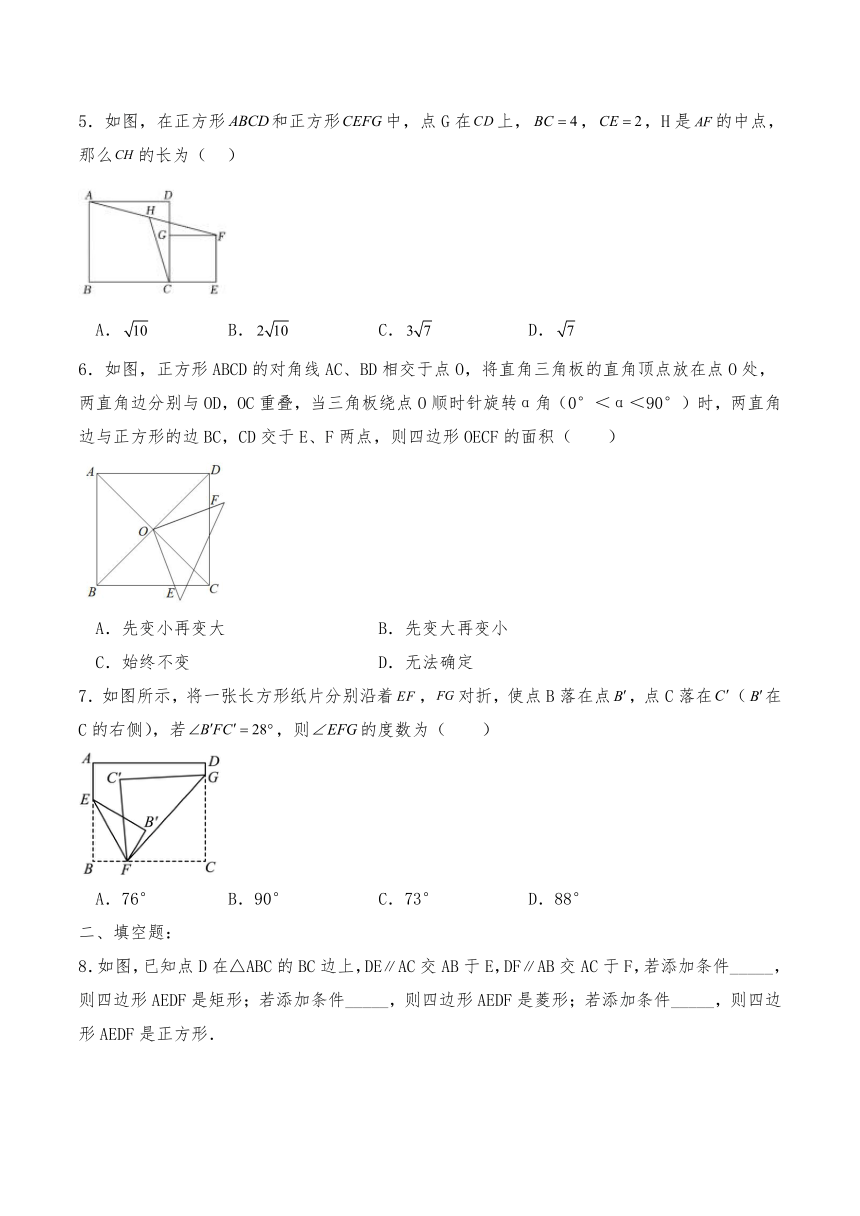
5.如图,在正方形和正方形中,点G在上,,,H是的中点,那么的长为( )
A. B. C. D.
6.如图,正方形ABCD的对角线AC、BD相交于点O,将直角三角板的直角顶点放在点O处,两直角边分别与OD,OC重叠,当三角板绕点O顺时针旋转α角(0°<α<90°)时,两直角边与正方形的边BC,CD交于E、F两点,则四边形OECF的面积( )
A.先变小再变大 B.先变大再变小
C.始终不变 D.无法确定
7.如图所示,将一张长方形纸片分别沿着,对折,使点B落在点,点C落在(在C的右侧),若,则的度数为( )
A.76° B.90° C.73° D.88°
二、填空题:
8.如图,已知点D在△ABC的BC边上,DEAC交AB于E,DFAB交AC于F,若添加条件_____,则四边形AEDF是矩形;若添加条件_____,则四边形AEDF是菱形;若添加条件_____,则四边形AEDF是正方形.
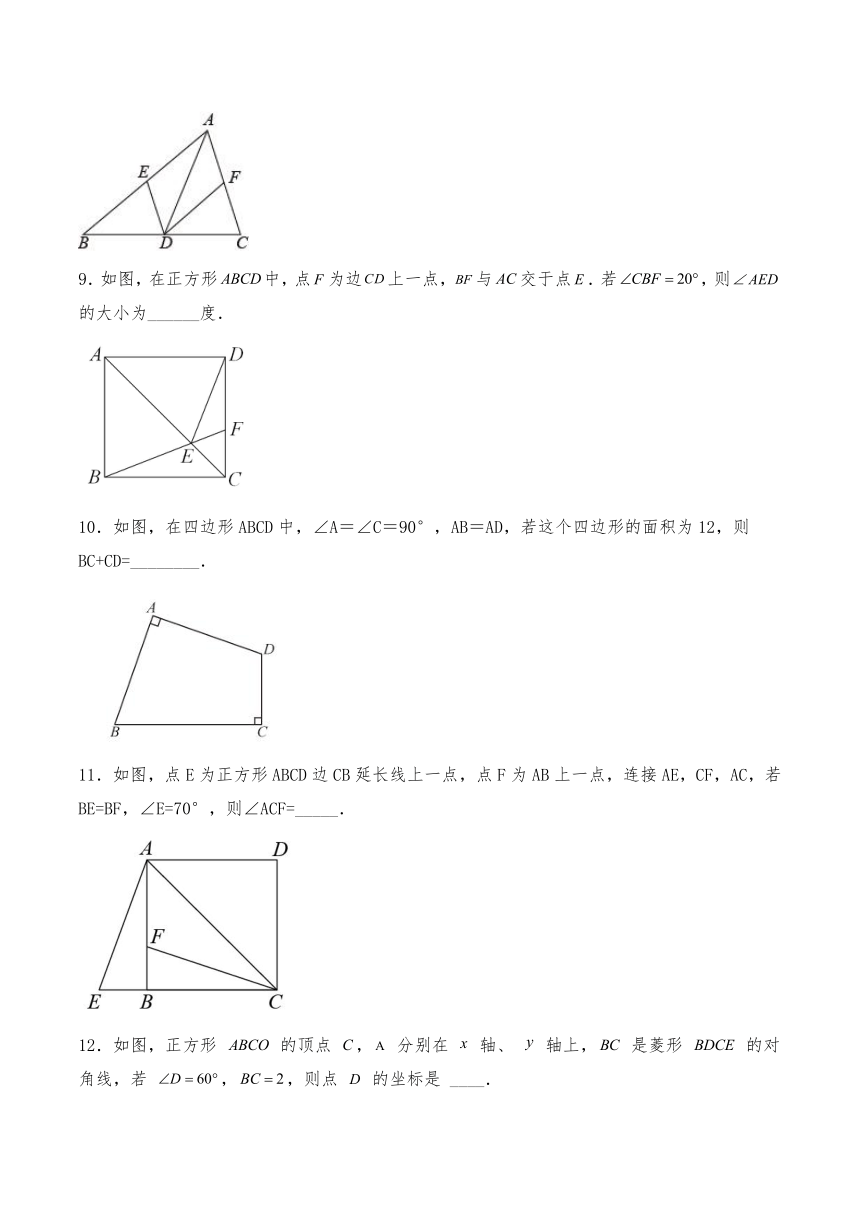
9.如图,在正方形中,点为边上一点,与交于点.若,则的大小为______度.
10.如图,在四边形ABCD中,∠A=∠C=90°,AB=AD,若这个四边形的面积为12,则BC+CD=________.
11.如图,点E为正方形ABCD边CB延长线上一点,点F为AB上一点,连接AE,CF,AC,若BE=BF,∠E=70°,则∠ACF=_____.
12.如图,正方形 的顶点 , 分别在 轴、 轴上, 是菱形 的对角线,若 ,,则点 的坐标是 ____.
13.如图,正方形的边长为4,点E在AB边上.四边形也为正方形,设的面积为S,则___________.
14.如图,在正方形中,为对角线上一点,过作于,于,若,,则___________.
三、解答题:
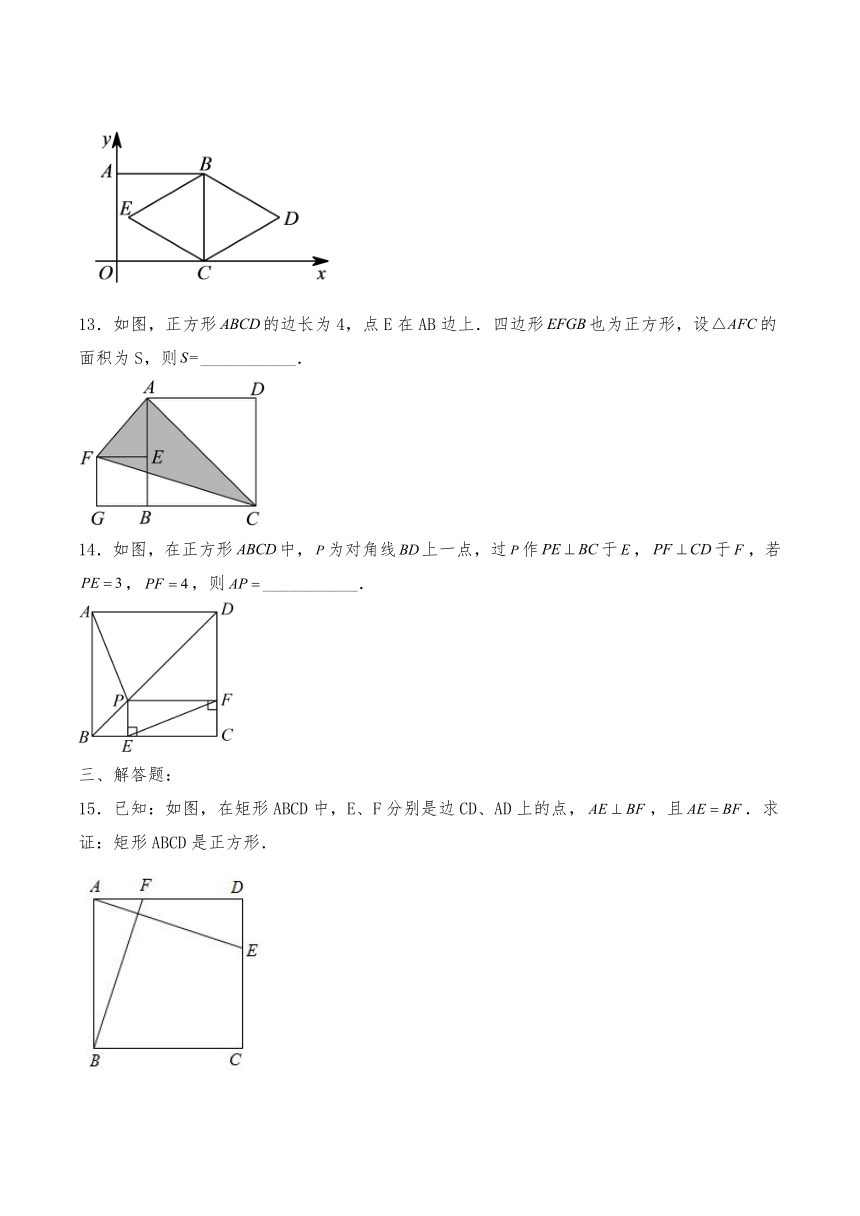
15.已知:如图,在矩形ABCD中,E、F分别是边CD、AD上的点,,且.求证:矩形ABCD是正方形.
16.如图,已知是边长为1的正方形对角线上一点,且.求:
(1)度数;
(2)的长.
17.如图,△ABC的中线AF与中位线DE相交于点O.
(1)求证:AF与DE互相平分;
(2)当△ABC满足___________时,四边形ADFE是正方形.
18.如图,正方形的边长为7,点是上的一点,且,将正方形沿翻折,点落在点处,延长交于点,求的长.
19.如图,在四边形纸片 ABCD 中,∠B=∠D=90°,点 E,F 分别在边 BC,CD 上,将 AB,AD 分别沿 AE,AF 折叠,点 B,D 恰好都和点 G 重合,∠EAF=45°.
(1)求证:四边形 ABCD 是正方形;
(2)若 EC=FC=1,求 AB 的长度.
20.如图,在中,点O是边上的一个动点,过点O作直线,设交的角平分线于点E,交的外角平分线于点F.
(1)求证:;
(2)当点O运动到何处时,四边形是矩形?并证明你的结论.
(3)当点O运动到何处,且满足什么条件时,四边形是正方形?并说明理由.
21.如图1,在正方形中,点E为上一点,连接,把沿折叠得到,延长交于G,连接.
(1)求证:.
(2)如图2,E为的中点,连接.
①求证:;②若正方形边长为6,求线段的长.
答案
一、单选题:
1.D
【分析】直接利用三角形中位线的性质以及正方形的判定方法分析得出答案.
【详解】解:使四边形为正方形,应添加的条件分别是且.
理由:∵顺次连接四边形各边中点得到四边形,
∴,,,,
,,,,
∴,,
∴四边形是平行四边形,
∵,
∴,
∴平行四边形是菱形,
∵,
∴,
∵,
,
∵,
∴,
∴菱形是正方形.
故选:D.
2.A
【分析】根据正方形的性质与判定,菱形的性质进行判断即可.
【详解】解:正方形是特殊的菱形,而菱形不一定是正方形;
菱形的对角线互相垂直, 而对角线互相垂直的四边形不一定是菱形;
正方形拥有菱形的一切性质,故②可以推出③和①,③可以推出①,而①推不出②和③,③推不出②;
故选:A.
3.A
【分析】如图,首先将旋转到,然后利用三角形全等的性质得到,,结合题中条件可以得出,再根据,和勾股定理,可以求出的长即可求解.
【详解】如图所示,将绕顺时针旋转得到,
∴,
∴,
∴,
∴、、三点共线,
∴,,
∵,,
∴,
∴,
∴,
在和中
,
∴(SAS)
∴,
设,
∵,,
∴,
∴,,
∴,
∵,
∴,
∴,
解得:
∴的长为
故选:A
4.B
【分析】如图,过点作轴于、轴于,则四边形是矩形可得、,再由A、B的坐标结合图形可得,然后再证明可得,进而确定OD的长即可解答.
【详解】解:如图,过点作轴于,轴于,
轴,轴,,
四边形是矩形,
,,
点、,
,,
,
四边形是正方形,
,,
,
在和中,
,
∴,
,
,
点.
故选:B.
5.A
【分析】连接、,如图,根据正方形的性质得,,,,则,再利用勾股定理计算出,然后根据直角三角形斜边上的中线求CH的长.
【详解】解:连接、,如图,
∵四边形和四边形都是正方形,,,
∴,,,,
∴,
在中,,
∵H是的中点,
∴ .
故选A.
6.C
【分析】依据正方形的性质,即可得到△OEC≌△OFD(ASA),进而得出,根据四边形OECF的面积等于,即可得到结论.
【详解】解:∵四边形ABCD是正方形,
∴OC=OD,∠ODC=∠OCB=45°,OC⊥OD,即∠COD=90°,
∴∠EOF=90°=∠COD,
又∵OC=OD,∠ODC=∠OCB=45°,
∴△OEC≌△OFD(ASA),
∴,
∴
∴四边形OECF的面积始终不变.
故选:C.
7.A
【分析】根据折叠的性质有:,,再根据,,可得,问题随之得解.
【详解】根据折叠的性质有:,,
∵,,
∴,
∵,,
∴,
∴,
∴,
故选:A.
二、填空题:
8. ∠BAC=90° AD平分∠BAC ∠BAC=90°且AD平分∠BAC(答案不唯一)
【分析】先利用平行四边形的判定方法得到四边形AEDF为平行四边形,然后根据矩形、菱形和正方形的判定方法添加条件.
【详解】解:∵DE∥AC交AB于E,DF∥AB交AC于F,
∴四边形AEDF为平行四边形,
∴当∠BAC=90°时,四边形AEDF是矩形;
当AD平分∠BAC时,四边形AEDF是菱形;
∠BAC=90°且AD平分∠BAC,四边形AEDF是正方形.
,∠BAC=90°,
故答案为∠BAC=90°,AD平分∠BAC,∠BAC=90°且AD平分∠BAC.
9.65
【分析】由三角形的外角性质可知:要求,只要求,由正方形的轴对称性质可知:∠CDE=∠CBF,即可求出.
【详解】解:四边形是正方形,具有关于对角线所在直线对称的对称性,
,,,
又是的外角,
,
故答案为:65.
10.4
【分析】延长CB到E,使BE=DC,连接AE,AC,推出∠ABE=∠D,由BE=DC,AB=AD,证明△ABE≌△ADC,得到AE=AC,∠EAB=∠DAC,∠EAC=90°,由勾股定理得,又S△AEC=S四边形ABCD=12,求得=12,计算出EC=4,即可求出答案.
【详解】延长CB到E,使BE=DC,连接AE,AC,
∵∠ABE=∠BAC+∠ACB,∠D=180°﹣∠DAC﹣∠DCA,
又∵∠BAD=90°,∠BCD=90°,
∴∠BAC+∠ACB=90°+90°﹣∠DAC﹣∠DCA=180°﹣∠DAC﹣∠DCA,
∴∠ABE=∠D,
又∵BE=DC,AB=AD,
∴△ABE≌△ADC,
∴AE=AC,∠EAB=∠DAC,
∴∠EAC=90°,
∵,
∴S△AEC=AE2=,
∵S△AEC=S四边形ABCD=12,
∴=12,
∴EC=4,
∴BC+CD=BC+BE=EC=4.
故答案为:4.
11.25°
【分析】根据全等三角形的判定和性质得出∠BCF=∠EAB,再利用正方形的性质解答即可.
【详解】解:∵正方形ABCD,
∴AB=BC,∠ABE=∠CBF=90°,
在△ABE与△CBF中
,
∴△ABE≌△CBF(SAS),
∴∠BCF=∠EAB,
∵∠E=70°,
∴∠BCF=∠EAB=90°-70°=20°,
∵正方形ABCD,AC是对角线,
∴∠ACB=45°,
∴∠ACF=45°-20°=25°.
故答案为:25°.
12.
【分析】过点作轴于点,根据四边形是菱形可知,,可得出是等边三角形,由此求出及的长即可得出结论.
【详解】解:过点作轴于点,
∵四边形是菱形,
∴,,
∴是等边三角形,
∵,
∴,
又∵四边形是正方形,
∴,,
∴,
∴,则,
∴,
∴.
13.8
【分析】连接,易得,利用等底等高将S转化成,代值计算即可.
【详解】解:连接,
∵四边形和四边形是正方形,
∴,
∴,
∴,
故答案为:8.
14.
【分析】延长、交、于、,由正方形的性质,得到,再由等腰三角形的性质及正方形的性质得到,,由勾股定理即可得出结论.
【详解】解:如图,延长、交、于、.
四边形为正方形,
,
,,
则 .
故答案为:.
三、解答题:
15.证明:∵四边形ABCD是矩形,
∴,
∴,
∵,
∴,
∴,
在△ABF和△DAE中,
∴,
∴,
∴矩形ABCD是正方形.
16.
(1)
解:∵是正方形,
∴,
∵,
∴
∴;
(2)
解:∵是正方形,
∴
∴,
∵
∴.
17.
(1)
证明:∵△ABC的中线AF与中位线DE相交于点O,
∴EF是△ABC的中位线,AD=BD,
∴EFAB,EFAB=AD,
∴四边形DFEA是平行四边形,
∴AF与DE互相平分.
(2)
解:当△ABC满足AB=AC,∠BAC=90°时,四边形ADFE是正方形,
理由如下:
由(1)得:四边形ADFE是平行四边形,
∵AB=AC,
∴△ABC是等腰三角形,
∵AF是△ABC的中线,
∴AF⊥BC,
∵DE是△ABC的中位线,
∴DEBC,
∴AF⊥DE,
∴平行四边形ADFE是菱形.
又∵∠BAC=90°,
∴四边形ADFE是正方形.
故答案为:AB=AC,∠BAC=90°.
18.解:连接,如图:
将正方形沿翻折,点落在点处,
,,,
,
,
,
,
设,则,,
,
,
解得,
的长为.
19.(1)由折叠性质知:∠BAE=∠EAG,∠DAF=∠FAG,
∵∠EAF=45°,
∴∠BAD=2∠EAF=245°=90°,
又∵∠B=∠D=90°,
∴四边形ABCD是矩形,
由折叠性质知:AB=AG,AD=AG,
∴AB=AD,
∴四边形ABCD是正方形;
(2)∵EC=FC=1,
∴BE=DF,EF=,
∵EF=EG+GF=BE+DF,
∴BE=DF=EF=,
∴AB=BC=BE+EC=.
20.(1)解:
∵,
∴,
又∵平分,
∴,
∴,
∴,
同理:,
∴.
(2)解:当点O运动到的中点时,四边形是矩形.
∵当点O运动到的中点时,,
又∵,
∴四边形是平行四边形,
由(1)可知,,
∴,
∴,即,
∴四边形是矩形.
(3)解:当点O运动到的中点时,且满足的直角三角形时,四边形是正方形.
∵由(2)知,当点O运动到的中点时,四边形是矩形,
∵,
∴,
∵,
∴,
∴,
∴四边形是正方形.
21.(1)证明:如图1:∵四边形是正方形,
.,
沿折叠得到,
,,,
,,
在和中,
,
,
,
,
,
,
;
(2)证明:如图2所示:
沿折叠得到,为的中点,
,,
,
,
,
,
即,
;
②解:设,则,,
正方形边长为6,为的中点,
,
,
在中,根据勾股定理得:,
解得:,
即线段的长为2.
一、单选题:
1.如图所示,顺次连接四边形各边中点得到四边形,使四边形为正方形,应添加的条件分别是( )
A.且 B.且
C.且 D.且
2.下列是关于某个四边形的三个结论:①它的对角线互相垂直;②它是一个正方形;③它是一个菱形.下列推理过程正确的是( )
A.由②推出③,由③推出① B.由①推出②,由②推出③
C.由③推出①,由①推出③ D.由①推出③,由③推出②
3.如图,在边长为5的正方形内作,交于点,交于点,连接,若,则的长为( )
A. B. C. D.2
4.如图,把正方形放在直角坐标系中,直角顶点落在第二象限,顶点、分别落在轴、轴上,已知点、,则点的坐标为( )
A.(-4,0) B. C. D.
5.如图,在正方形和正方形中,点G在上,,,H是的中点,那么的长为( )
A. B. C. D.
6.如图,正方形ABCD的对角线AC、BD相交于点O,将直角三角板的直角顶点放在点O处,两直角边分别与OD,OC重叠,当三角板绕点O顺时针旋转α角(0°<α<90°)时,两直角边与正方形的边BC,CD交于E、F两点,则四边形OECF的面积( )
A.先变小再变大 B.先变大再变小
C.始终不变 D.无法确定
7.如图所示,将一张长方形纸片分别沿着,对折,使点B落在点,点C落在(在C的右侧),若,则的度数为( )
A.76° B.90° C.73° D.88°
二、填空题:
8.如图,已知点D在△ABC的BC边上,DEAC交AB于E,DFAB交AC于F,若添加条件_____,则四边形AEDF是矩形;若添加条件_____,则四边形AEDF是菱形;若添加条件_____,则四边形AEDF是正方形.
9.如图,在正方形中,点为边上一点,与交于点.若,则的大小为______度.
10.如图,在四边形ABCD中,∠A=∠C=90°,AB=AD,若这个四边形的面积为12,则BC+CD=________.
11.如图,点E为正方形ABCD边CB延长线上一点,点F为AB上一点,连接AE,CF,AC,若BE=BF,∠E=70°,则∠ACF=_____.
12.如图,正方形 的顶点 , 分别在 轴、 轴上, 是菱形 的对角线,若 ,,则点 的坐标是 ____.
13.如图,正方形的边长为4,点E在AB边上.四边形也为正方形,设的面积为S,则___________.
14.如图,在正方形中,为对角线上一点,过作于,于,若,,则___________.
三、解答题:
15.已知:如图,在矩形ABCD中,E、F分别是边CD、AD上的点,,且.求证:矩形ABCD是正方形.
16.如图,已知是边长为1的正方形对角线上一点,且.求:
(1)度数;
(2)的长.
17.如图,△ABC的中线AF与中位线DE相交于点O.
(1)求证:AF与DE互相平分;
(2)当△ABC满足___________时,四边形ADFE是正方形.
18.如图,正方形的边长为7,点是上的一点,且,将正方形沿翻折,点落在点处,延长交于点,求的长.
19.如图,在四边形纸片 ABCD 中,∠B=∠D=90°,点 E,F 分别在边 BC,CD 上,将 AB,AD 分别沿 AE,AF 折叠,点 B,D 恰好都和点 G 重合,∠EAF=45°.
(1)求证:四边形 ABCD 是正方形;
(2)若 EC=FC=1,求 AB 的长度.
20.如图,在中,点O是边上的一个动点,过点O作直线,设交的角平分线于点E,交的外角平分线于点F.
(1)求证:;
(2)当点O运动到何处时,四边形是矩形?并证明你的结论.
(3)当点O运动到何处,且满足什么条件时,四边形是正方形?并说明理由.
21.如图1,在正方形中,点E为上一点,连接,把沿折叠得到,延长交于G,连接.
(1)求证:.
(2)如图2,E为的中点,连接.
①求证:;②若正方形边长为6,求线段的长.
答案
一、单选题:
1.D
【分析】直接利用三角形中位线的性质以及正方形的判定方法分析得出答案.
【详解】解:使四边形为正方形,应添加的条件分别是且.
理由:∵顺次连接四边形各边中点得到四边形,
∴,,,,
,,,,
∴,,
∴四边形是平行四边形,
∵,
∴,
∴平行四边形是菱形,
∵,
∴,
∵,
,
∵,
∴,
∴菱形是正方形.
故选:D.
2.A
【分析】根据正方形的性质与判定,菱形的性质进行判断即可.
【详解】解:正方形是特殊的菱形,而菱形不一定是正方形;
菱形的对角线互相垂直, 而对角线互相垂直的四边形不一定是菱形;
正方形拥有菱形的一切性质,故②可以推出③和①,③可以推出①,而①推不出②和③,③推不出②;
故选:A.
3.A
【分析】如图,首先将旋转到,然后利用三角形全等的性质得到,,结合题中条件可以得出,再根据,和勾股定理,可以求出的长即可求解.
【详解】如图所示,将绕顺时针旋转得到,
∴,
∴,
∴,
∴、、三点共线,
∴,,
∵,,
∴,
∴,
∴,
在和中
,
∴(SAS)
∴,
设,
∵,,
∴,
∴,,
∴,
∵,
∴,
∴,
解得:
∴的长为
故选:A
4.B
【分析】如图,过点作轴于、轴于,则四边形是矩形可得、,再由A、B的坐标结合图形可得,然后再证明可得,进而确定OD的长即可解答.
【详解】解:如图,过点作轴于,轴于,
轴,轴,,
四边形是矩形,
,,
点、,
,,
,
四边形是正方形,
,,
,
在和中,
,
∴,
,
,
点.
故选:B.
5.A
【分析】连接、,如图,根据正方形的性质得,,,,则,再利用勾股定理计算出,然后根据直角三角形斜边上的中线求CH的长.
【详解】解:连接、,如图,
∵四边形和四边形都是正方形,,,
∴,,,,
∴,
在中,,
∵H是的中点,
∴ .
故选A.
6.C
【分析】依据正方形的性质,即可得到△OEC≌△OFD(ASA),进而得出,根据四边形OECF的面积等于,即可得到结论.
【详解】解:∵四边形ABCD是正方形,
∴OC=OD,∠ODC=∠OCB=45°,OC⊥OD,即∠COD=90°,
∴∠EOF=90°=∠COD,
又∵OC=OD,∠ODC=∠OCB=45°,
∴△OEC≌△OFD(ASA),
∴,
∴
∴四边形OECF的面积始终不变.
故选:C.
7.A
【分析】根据折叠的性质有:,,再根据,,可得,问题随之得解.
【详解】根据折叠的性质有:,,
∵,,
∴,
∵,,
∴,
∴,
∴,
故选:A.
二、填空题:
8. ∠BAC=90° AD平分∠BAC ∠BAC=90°且AD平分∠BAC(答案不唯一)
【分析】先利用平行四边形的判定方法得到四边形AEDF为平行四边形,然后根据矩形、菱形和正方形的判定方法添加条件.
【详解】解:∵DE∥AC交AB于E,DF∥AB交AC于F,
∴四边形AEDF为平行四边形,
∴当∠BAC=90°时,四边形AEDF是矩形;
当AD平分∠BAC时,四边形AEDF是菱形;
∠BAC=90°且AD平分∠BAC,四边形AEDF是正方形.
,∠BAC=90°,
故答案为∠BAC=90°,AD平分∠BAC,∠BAC=90°且AD平分∠BAC.
9.65
【分析】由三角形的外角性质可知:要求,只要求,由正方形的轴对称性质可知:∠CDE=∠CBF,即可求出.
【详解】解:四边形是正方形,具有关于对角线所在直线对称的对称性,
,,,
又是的外角,
,
故答案为:65.
10.4
【分析】延长CB到E,使BE=DC,连接AE,AC,推出∠ABE=∠D,由BE=DC,AB=AD,证明△ABE≌△ADC,得到AE=AC,∠EAB=∠DAC,∠EAC=90°,由勾股定理得,又S△AEC=S四边形ABCD=12,求得=12,计算出EC=4,即可求出答案.
【详解】延长CB到E,使BE=DC,连接AE,AC,
∵∠ABE=∠BAC+∠ACB,∠D=180°﹣∠DAC﹣∠DCA,
又∵∠BAD=90°,∠BCD=90°,
∴∠BAC+∠ACB=90°+90°﹣∠DAC﹣∠DCA=180°﹣∠DAC﹣∠DCA,
∴∠ABE=∠D,
又∵BE=DC,AB=AD,
∴△ABE≌△ADC,
∴AE=AC,∠EAB=∠DAC,
∴∠EAC=90°,
∵,
∴S△AEC=AE2=,
∵S△AEC=S四边形ABCD=12,
∴=12,
∴EC=4,
∴BC+CD=BC+BE=EC=4.
故答案为:4.
11.25°
【分析】根据全等三角形的判定和性质得出∠BCF=∠EAB,再利用正方形的性质解答即可.
【详解】解:∵正方形ABCD,
∴AB=BC,∠ABE=∠CBF=90°,
在△ABE与△CBF中
,
∴△ABE≌△CBF(SAS),
∴∠BCF=∠EAB,
∵∠E=70°,
∴∠BCF=∠EAB=90°-70°=20°,
∵正方形ABCD,AC是对角线,
∴∠ACB=45°,
∴∠ACF=45°-20°=25°.
故答案为:25°.
12.
【分析】过点作轴于点,根据四边形是菱形可知,,可得出是等边三角形,由此求出及的长即可得出结论.
【详解】解:过点作轴于点,
∵四边形是菱形,
∴,,
∴是等边三角形,
∵,
∴,
又∵四边形是正方形,
∴,,
∴,
∴,则,
∴,
∴.
13.8
【分析】连接,易得,利用等底等高将S转化成,代值计算即可.
【详解】解:连接,
∵四边形和四边形是正方形,
∴,
∴,
∴,
故答案为:8.
14.
【分析】延长、交、于、,由正方形的性质,得到,再由等腰三角形的性质及正方形的性质得到,,由勾股定理即可得出结论.
【详解】解:如图,延长、交、于、.
四边形为正方形,
,
,,
则 .
故答案为:.
三、解答题:
15.证明:∵四边形ABCD是矩形,
∴,
∴,
∵,
∴,
∴,
在△ABF和△DAE中,
∴,
∴,
∴矩形ABCD是正方形.
16.
(1)
解:∵是正方形,
∴,
∵,
∴
∴;
(2)
解:∵是正方形,
∴
∴,
∵
∴.
17.
(1)
证明:∵△ABC的中线AF与中位线DE相交于点O,
∴EF是△ABC的中位线,AD=BD,
∴EFAB,EFAB=AD,
∴四边形DFEA是平行四边形,
∴AF与DE互相平分.
(2)
解:当△ABC满足AB=AC,∠BAC=90°时,四边形ADFE是正方形,
理由如下:
由(1)得:四边形ADFE是平行四边形,
∵AB=AC,
∴△ABC是等腰三角形,
∵AF是△ABC的中线,
∴AF⊥BC,
∵DE是△ABC的中位线,
∴DEBC,
∴AF⊥DE,
∴平行四边形ADFE是菱形.
又∵∠BAC=90°,
∴四边形ADFE是正方形.
故答案为:AB=AC,∠BAC=90°.
18.解:连接,如图:
将正方形沿翻折,点落在点处,
,,,
,
,
,
,
设,则,,
,
,
解得,
的长为.
19.(1)由折叠性质知:∠BAE=∠EAG,∠DAF=∠FAG,
∵∠EAF=45°,
∴∠BAD=2∠EAF=245°=90°,
又∵∠B=∠D=90°,
∴四边形ABCD是矩形,
由折叠性质知:AB=AG,AD=AG,
∴AB=AD,
∴四边形ABCD是正方形;
(2)∵EC=FC=1,
∴BE=DF,EF=,
∵EF=EG+GF=BE+DF,
∴BE=DF=EF=,
∴AB=BC=BE+EC=.
20.(1)解:
∵,
∴,
又∵平分,
∴,
∴,
∴,
同理:,
∴.
(2)解:当点O运动到的中点时,四边形是矩形.
∵当点O运动到的中点时,,
又∵,
∴四边形是平行四边形,
由(1)可知,,
∴,
∴,即,
∴四边形是矩形.
(3)解:当点O运动到的中点时,且满足的直角三角形时,四边形是正方形.
∵由(2)知,当点O运动到的中点时,四边形是矩形,
∵,
∴,
∵,
∴,
∴,
∴四边形是正方形.
21.(1)证明:如图1:∵四边形是正方形,
.,
沿折叠得到,
,,,
,,
在和中,
,
,
,
,
,
,
;
(2)证明:如图2所示:
沿折叠得到,为的中点,
,,
,
,
,
,
即,
;
②解:设,则,,
正方形边长为6,为的中点,
,
,
在中,根据勾股定理得:,
解得:,
即线段的长为2.
