1.2从立体图形到平面图形(三)柱体、锥体展开图 课件(共21张PPT) 2024-2025学年六年级数学上册鲁教版(2024)
文档属性
| 名称 | 1.2从立体图形到平面图形(三)柱体、锥体展开图 课件(共21张PPT) 2024-2025学年六年级数学上册鲁教版(2024) |

|
|
| 格式 | pptx | ||
| 文件大小 | 4.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-01-24 00:00:00 | ||
图片预览

文档简介
(共21张PPT)
1.2从立体图形到平面图形(三)
----柱体、锥体展开图
鲁教版(2024)六年级上册
第一章 丰富的图形世界
新课导入
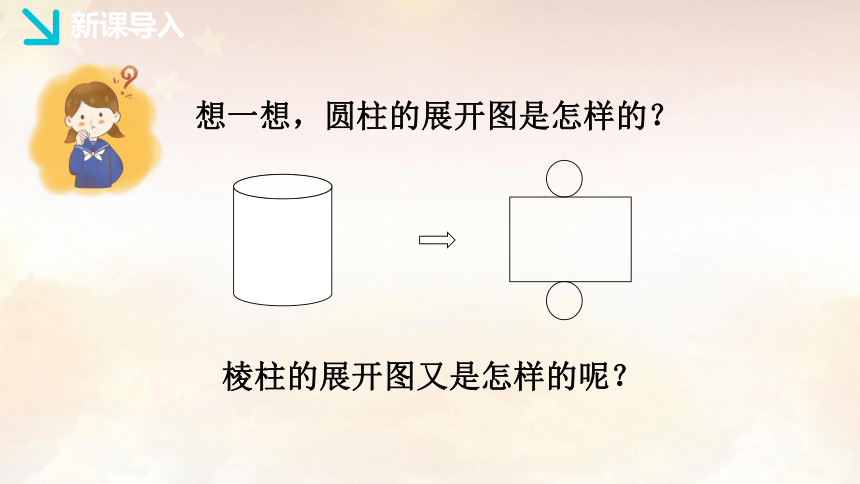
想一想,圆柱的展开图是怎样的?
棱柱的展开图又是怎样的呢?
新课讲解
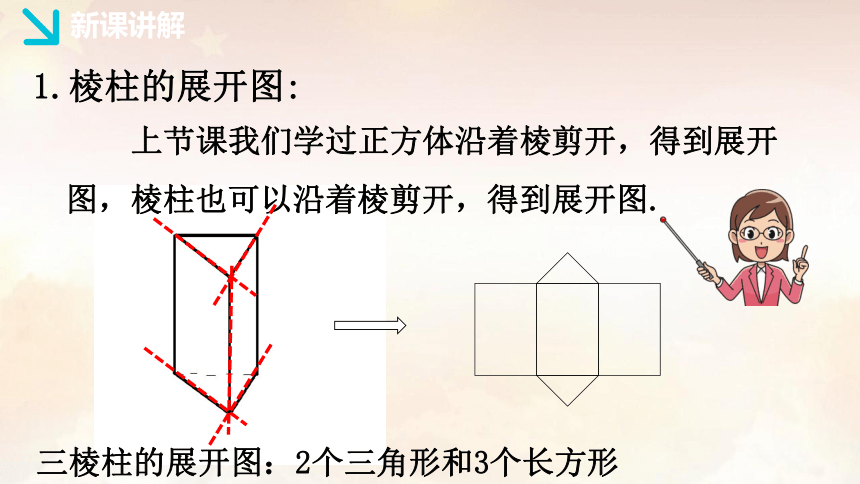
上节课我们学过正方体沿着棱剪开,得到展开图,棱柱也可以沿着棱剪开,得到展开图.
三棱柱的展开图:2个三角形和3个长方形
1.棱柱的展开图:
新课讲解
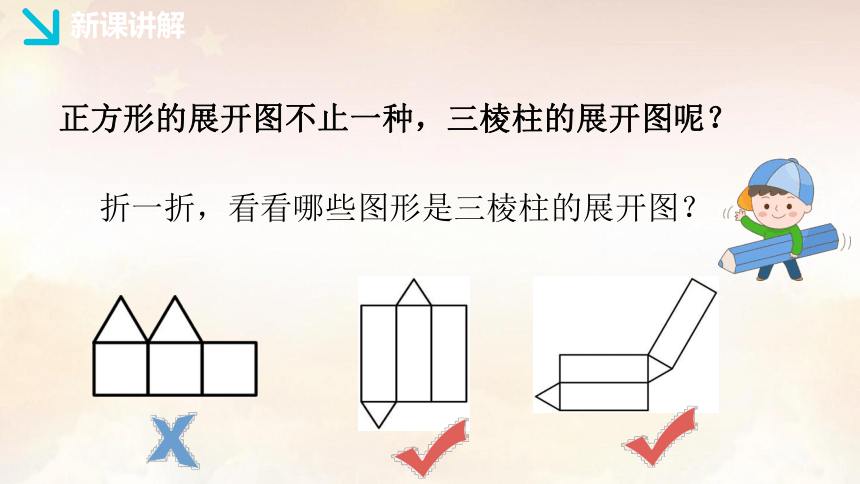
正方形的展开图不止一种,三棱柱的展开图呢?
折一折,看看哪些图形是三棱柱的展开图?
新课讲解
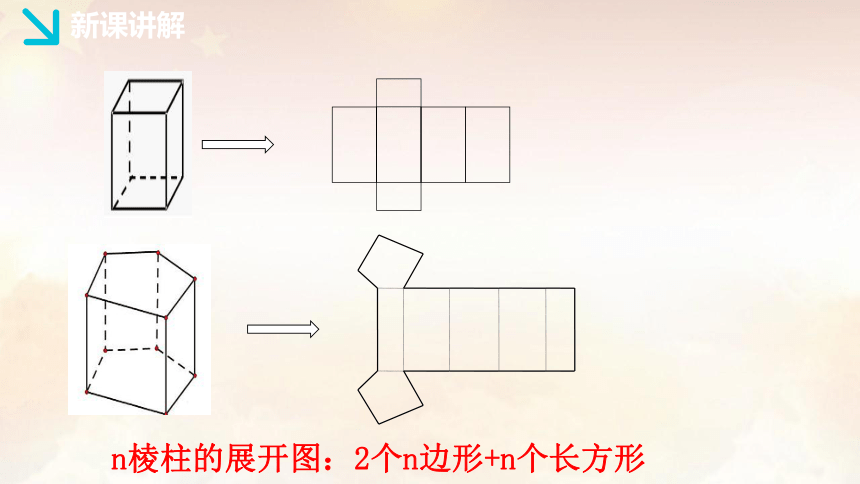
n棱柱的展开图:2个n边形+n个长方形
新课讲解
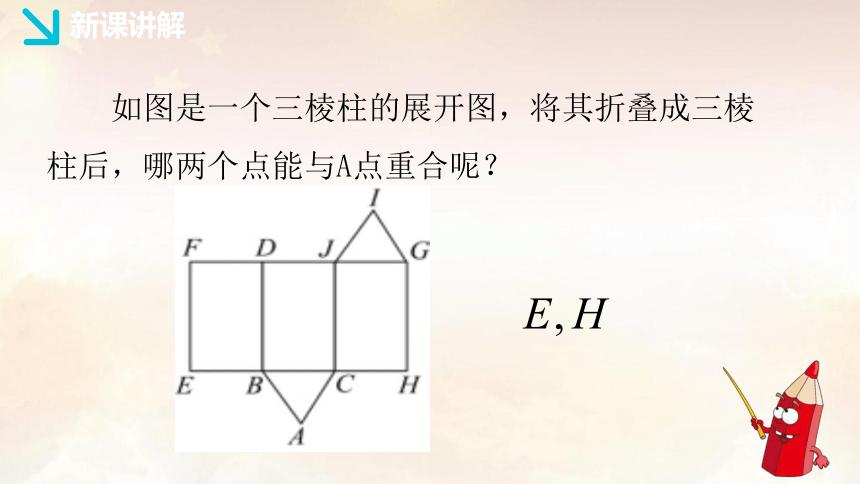
如图是一个三棱柱的展开图,将其折叠成三棱柱后,哪两个点能与A点重合呢?
课堂练习
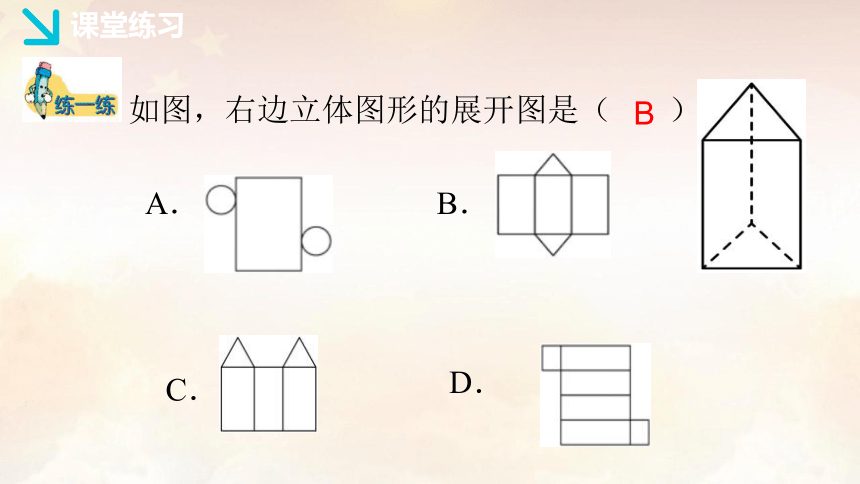
如图,右边立体图形的展开图是( )
A.
B.
C.
D.
B
课堂练习
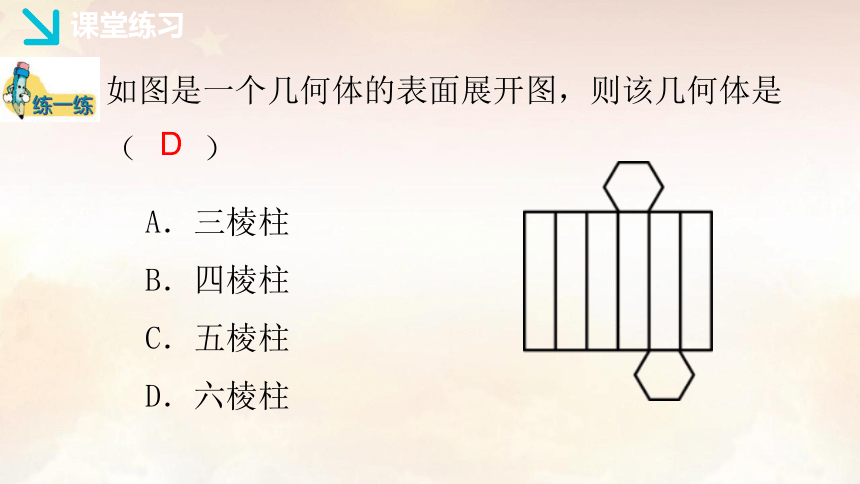
如图是一个几何体的表面展开图,则该几何体是
( )
A.三棱柱
B.四棱柱
C.五棱柱
D.六棱柱
D
新课讲解
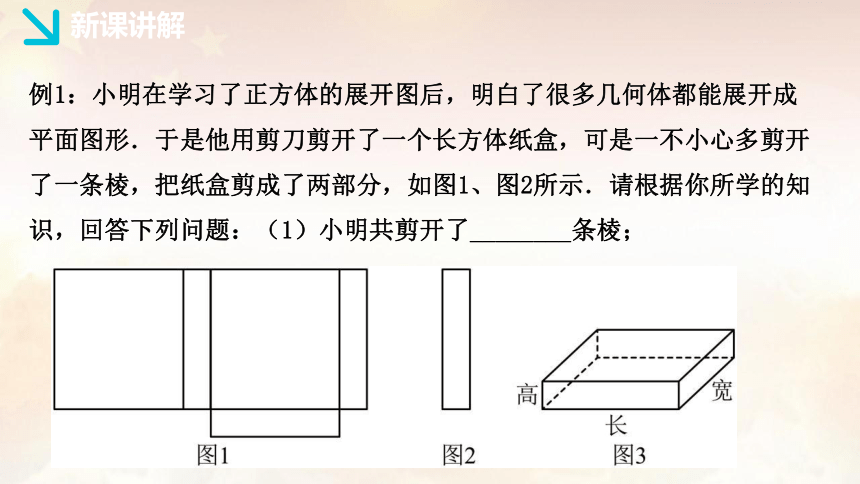
例1:小明在学习了正方体的展开图后,明白了很多几何体都能展开成平面图形.于是他用剪刀剪开了一个长方体纸盒,可是一不小心多剪开了一条棱,把纸盒剪成了两部分,如图1、图2所示.请根据你所学的知识,回答下列问题:(1)小明共剪开了________条棱;
新课讲解
分析:长方体一共是12条棱,展开图中有4条棱没有剪开,
所以剪开了8条棱。
解:小明共剪开了8条棱.
新课讲解
(2)现在小明想将剪断的图2重新粘贴到图1上去,而且经过折叠以后,仍然可以还原成一个长方体纸盒(如图3),小明在图1中补全图形有________种方法,请任选一种方法在图1中补全粘贴;
新课讲解
分析:长方体的展开图和正方体的展开图类似,
题中是”一四一型”.
解:如图,四种情况:
新课讲解
(3)经过测量,小明发现这个纸盒的底面是一个正方形,其边长是长方体的高的5倍,并且纸盒所有棱长的和是880cm,求这个纸盒的体积.
分析:设最短的棱长高为x cm,则长与宽相等为5x cm,根据棱
长的和是880 cm,列出方程可求出长宽高,即可求出长
方体纸盒的体积.
新课讲解
解:设最短的棱长高为x cm,则长与宽相等为5x cm,
由长方体纸盒所有棱长的和是880 cm,可得:
4(x+5x+5x)=880
解得:x=20
所以这个长方体纸盒的体积为20×100×100=200000(cm3)
新课讲解
总结:
1.判断棱柱剪了几条棱,用总棱条数-未减的数量;
2.四棱柱的展开图与正方体展开图类似。
新课讲解
想一想,圆锥的展开图是怎样的?
棱锥的展开图又是怎样的呢?
新课讲解
2.棱锥的展开图:
棱柱沿着棱剪开得到平面图,棱锥可以同样沿着棱剪开得到平面图。
新课讲解
你能画出三棱锥、五棱锥的展开图吗?想一想,它们有什么规律?
n棱锥的展开图:
1个n边形+n个三角形
课堂练习
1.如图是某几何体的展开图,该几何体是( )
A.三棱柱
B.三棱锥
C.圆柱
D.圆锥
D
新课讲解
2.某个几何体的平面展开图如图所示,则这个几何体为( )
A.四棱柱
B.四棱锥
C.圆柱
D.圆锥
B
课堂总结
2个n边形+n个长方形.
1.柱体的展开图:
圆柱的展开图:
n棱柱的展开图:
1个扇形+1个圆
1个长方形形+2个圆.
2.柱体的展开图:
圆锥的展开图:
n棱锥的展开图:
1个n边形+n个三角形
1.2从立体图形到平面图形(三)
----柱体、锥体展开图
鲁教版(2024)六年级上册
第一章 丰富的图形世界
新课导入
想一想,圆柱的展开图是怎样的?
棱柱的展开图又是怎样的呢?
新课讲解
上节课我们学过正方体沿着棱剪开,得到展开图,棱柱也可以沿着棱剪开,得到展开图.
三棱柱的展开图:2个三角形和3个长方形
1.棱柱的展开图:
新课讲解
正方形的展开图不止一种,三棱柱的展开图呢?
折一折,看看哪些图形是三棱柱的展开图?
新课讲解
n棱柱的展开图:2个n边形+n个长方形
新课讲解
如图是一个三棱柱的展开图,将其折叠成三棱柱后,哪两个点能与A点重合呢?
课堂练习
如图,右边立体图形的展开图是( )
A.
B.
C.
D.
B
课堂练习
如图是一个几何体的表面展开图,则该几何体是
( )
A.三棱柱
B.四棱柱
C.五棱柱
D.六棱柱
D
新课讲解
例1:小明在学习了正方体的展开图后,明白了很多几何体都能展开成平面图形.于是他用剪刀剪开了一个长方体纸盒,可是一不小心多剪开了一条棱,把纸盒剪成了两部分,如图1、图2所示.请根据你所学的知识,回答下列问题:(1)小明共剪开了________条棱;
新课讲解
分析:长方体一共是12条棱,展开图中有4条棱没有剪开,
所以剪开了8条棱。
解:小明共剪开了8条棱.
新课讲解
(2)现在小明想将剪断的图2重新粘贴到图1上去,而且经过折叠以后,仍然可以还原成一个长方体纸盒(如图3),小明在图1中补全图形有________种方法,请任选一种方法在图1中补全粘贴;
新课讲解
分析:长方体的展开图和正方体的展开图类似,
题中是”一四一型”.
解:如图,四种情况:
新课讲解
(3)经过测量,小明发现这个纸盒的底面是一个正方形,其边长是长方体的高的5倍,并且纸盒所有棱长的和是880cm,求这个纸盒的体积.
分析:设最短的棱长高为x cm,则长与宽相等为5x cm,根据棱
长的和是880 cm,列出方程可求出长宽高,即可求出长
方体纸盒的体积.
新课讲解
解:设最短的棱长高为x cm,则长与宽相等为5x cm,
由长方体纸盒所有棱长的和是880 cm,可得:
4(x+5x+5x)=880
解得:x=20
所以这个长方体纸盒的体积为20×100×100=200000(cm3)
新课讲解
总结:
1.判断棱柱剪了几条棱,用总棱条数-未减的数量;
2.四棱柱的展开图与正方体展开图类似。
新课讲解
想一想,圆锥的展开图是怎样的?
棱锥的展开图又是怎样的呢?
新课讲解
2.棱锥的展开图:
棱柱沿着棱剪开得到平面图,棱锥可以同样沿着棱剪开得到平面图。
新课讲解
你能画出三棱锥、五棱锥的展开图吗?想一想,它们有什么规律?
n棱锥的展开图:
1个n边形+n个三角形
课堂练习
1.如图是某几何体的展开图,该几何体是( )
A.三棱柱
B.三棱锥
C.圆柱
D.圆锥
D
新课讲解
2.某个几何体的平面展开图如图所示,则这个几何体为( )
A.四棱柱
B.四棱锥
C.圆柱
D.圆锥
B
课堂总结
2个n边形+n个长方形.
1.柱体的展开图:
圆柱的展开图:
n棱柱的展开图:
1个扇形+1个圆
1个长方形形+2个圆.
2.柱体的展开图:
圆锥的展开图:
n棱锥的展开图:
1个n边形+n个三角形
同课章节目录
