辽宁省五校(东北育才中学、辽宁省实验中学、大连24中学、大连八中、鞍山一中)2025届高三上学期期末考试 数学(PDF版,含答案)
文档属性
| 名称 | 辽宁省五校(东北育才中学、辽宁省实验中学、大连24中学、大连八中、鞍山一中)2025届高三上学期期末考试 数学(PDF版,含答案) |

|
|
| 格式 | |||
| 文件大小 | 1.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-01-22 00:00:00 | ||
图片预览




文档简介
2024—2025学年度上学期期末考试高三年级数学科答案
一、单项选择题:
1.A 2.C 3.D 4. C 5.B 6. A 7.B 8. C
二、多项选择题
9.AD 10.BC 11.BCD
三、填空题
12. ; 13.答案不唯一,4,5,6任写一个即可. 14.
四、解答题
15.解:
(I) ……5分
所以 …………………………………………………………6分
(II)由 = ,
所以 ………………………7分
设 ,由点 在 边上,且 为锐角三角形,所以 ,
所以 .……………………………………………………………9分
在 中,由 ,
所以 ,所以 ,
所以 …………11分
由 是定义域上的减函数,所以 ,
所以 的范围为 .…………13分(其它方法酌情给分)
16.解:(I)由椭圆离心率 ,所以 .………………………1分
所以椭圆方程化为 .
由直线 的斜率 ,所以直线 的方程为 ,……………2分
由椭圆对称性,不妨设点
联立 ,解得 .…………………………………………4分
所以 ,解得 ,……6分
所以椭圆 的方程为 ……………………7分
(II)如图,延长 交 于点 ,
由(1)可知 ,
设 ,设 的方程为 ,
由 ,得 ,故 ………9分
设 与 的距离为 ,四边形 的面积为 ,
由 及椭圆的对称性可知,点 与点 关于原点对称.
所以 …11分
又因为 …13分
当且仅当 ,即 时,等号成立,…………………14分
故四边形 面积的最大值为 2.……………………………15分
17.解:(I)甲同学所有可能的选择答案有 种,
其中正确选项只有一个,设 M=“猜对本题得 6分”,故 .……………3分
(II)乙同学所有可能的选择答案有 种,即共有 10个样本点,
设乙同学本题可能得分为 ,则 的可能取值为 0,4,6.
, , …………………………7分
所以乙同学可能得分的分布列为
0 4 6
所以期望 …………………………………9分
(III)由题意得丙得 0分的概率为 ,丁得 0分的概率为 ,…10分
丙丁总分刚好得 18分的情况包含:
事件 A:丙得 12分有 6+6一种情况,丁得 6分有 6+0,0+6,3+3三种情况,
则 ;
事件 B:丙得 9分有 6+3,3+6两种情况,丁得 9分有 6+3,3+6两种情况,
则 ;
事件 C:丙得 6分有 6+0,0+6,3+3三种情况,丁得 12分有 6+6一种情况,
则 ;…………………………………14分
所以丙丁总分刚好得 18分的概率 .…………15分
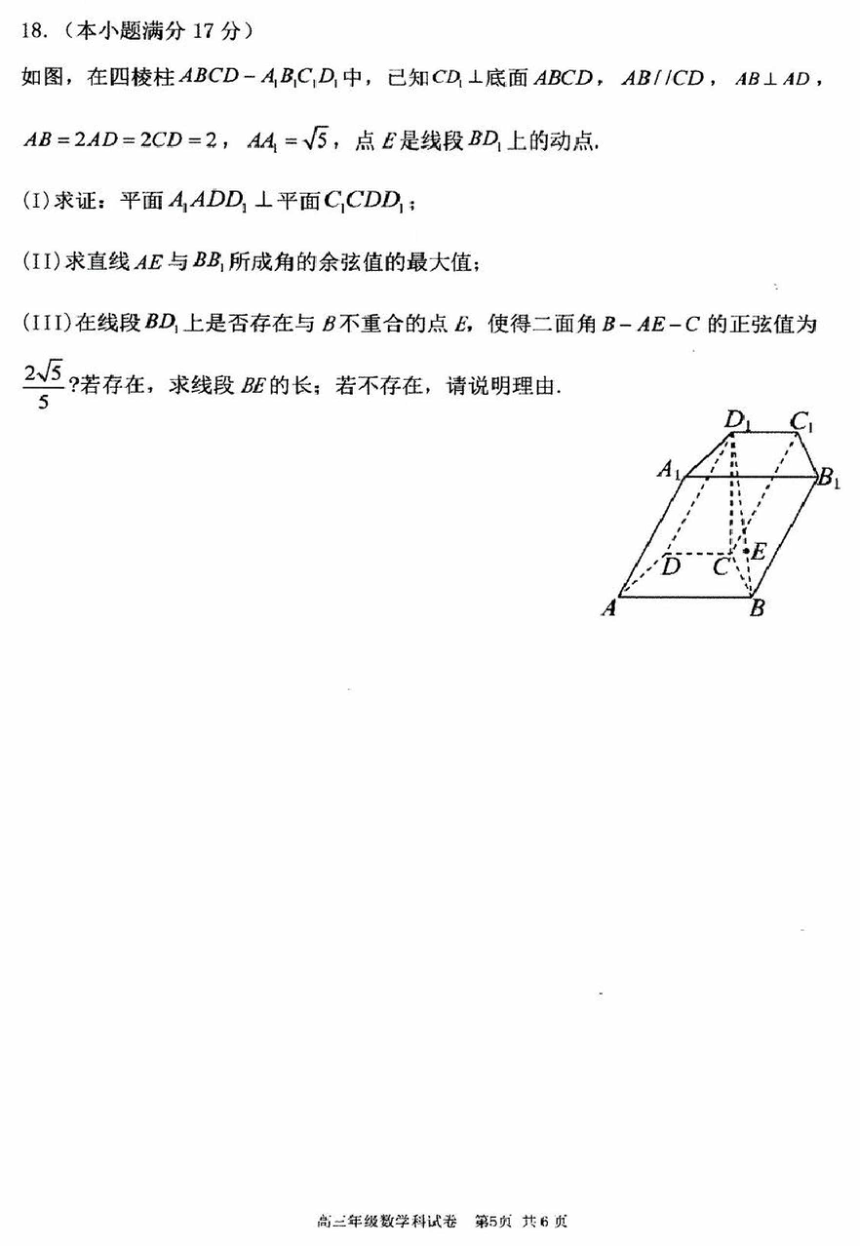
18.解:(I)由 , ,所以 .
由 平面 ,所以 .
由 , , ,所以平面 平面 .…4分
(II)取 中点 ,连接 ,
在梯形 中,因为 , ,所以 , ,
则在 中, ,由 ,则 ,………………6分
易知 两两垂直,分别以 为 轴,建立空间直角坐标系,
如下图所示:
在四棱柱 中, ,则 ,
因为 平面 , 平面 ,所以 ,
在 中, ,
则 , , , ,
取 , , ,
设平面 的法向量为 ,可得 ,则 ,
取 ,则 ,所以平面 的一个法向量 ,……………8分
设点 到平面 的距离 ,
设直线 与平面 所成角为 ,则 ,即 ,
在四棱柱 中,因为 ,且 平面 ,
所以当直线 与 所成角为 时,其余弦值取得最大值,即为 .……10分
(III)由题意作图如下:由题可知
, , ,
因为 ,所以 ,则 , ,
,
设
平面 的法向量 ,可得 ,
则 ,令 ,则 ,
所以平面 的一个法向量 ,
设平面 的法向量 ,可得 ,
则 ,令 ,则 ,
所以平面 的一个法向量 ,…………………………14分
设二面角 的大小为 ,
则 ,
由二面角 的正弦值为 ,则 ,
可得 ,化简可得 ,解得 或 ,…………16分
由 ,则 ,故存在, .………………17分
19.解:
(I)因为 单调递增,不存在正数 ,使得 恒成立,
所以数列 不具有性质 .………………………………………………………2分
因为 ,又数列 为单调递减数列,所以数列 具有性质 .……4分
(II)因为 ,
若 为奇数的概率为 为偶数的概率为 ,
①………………
………………6分
② ,
……………………………………7分
,即 .………………………………………8分
所以当 时, ,故 随着 的增大而增大,且 .
故数列 具有性质 .……………………………10分
(III)令 ,则 , , ,
所以当 时, 在 上递减,而 ,
故 在 有唯一的零点 ,即 ,即 ………………12分
且当 时, ,即 ,
当 时, ,即
由 ,可知 ,
在 上单调递增;……………………………………………………………13分
由 ,
所以 ,
所以 ,……………………14分
假设 时, 成立,
则 ,即 成立,
结合 可得:对于任意 恒成立,
故 为递增数列, 为递减数列.…………………………………………16分
对数列 ,存在 ,使 ,所以数列 具有性质
对数列 ,存在 ,使 ,所以数列 也具有性质 ……17分
一、单项选择题:
1.A 2.C 3.D 4. C 5.B 6. A 7.B 8. C
二、多项选择题
9.AD 10.BC 11.BCD
三、填空题
12. ; 13.答案不唯一,4,5,6任写一个即可. 14.
四、解答题
15.解:
(I) ……5分
所以 …………………………………………………………6分
(II)由 = ,
所以 ………………………7分
设 ,由点 在 边上,且 为锐角三角形,所以 ,
所以 .……………………………………………………………9分
在 中,由 ,
所以 ,所以 ,
所以 …………11分
由 是定义域上的减函数,所以 ,
所以 的范围为 .…………13分(其它方法酌情给分)
16.解:(I)由椭圆离心率 ,所以 .………………………1分
所以椭圆方程化为 .
由直线 的斜率 ,所以直线 的方程为 ,……………2分
由椭圆对称性,不妨设点
联立 ,解得 .…………………………………………4分
所以 ,解得 ,……6分
所以椭圆 的方程为 ……………………7分
(II)如图,延长 交 于点 ,
由(1)可知 ,
设 ,设 的方程为 ,
由 ,得 ,故 ………9分
设 与 的距离为 ,四边形 的面积为 ,
由 及椭圆的对称性可知,点 与点 关于原点对称.
所以 …11分
又因为 …13分
当且仅当 ,即 时,等号成立,…………………14分
故四边形 面积的最大值为 2.……………………………15分
17.解:(I)甲同学所有可能的选择答案有 种,
其中正确选项只有一个,设 M=“猜对本题得 6分”,故 .……………3分
(II)乙同学所有可能的选择答案有 种,即共有 10个样本点,
设乙同学本题可能得分为 ,则 的可能取值为 0,4,6.
, , …………………………7分
所以乙同学可能得分的分布列为
0 4 6
所以期望 …………………………………9分
(III)由题意得丙得 0分的概率为 ,丁得 0分的概率为 ,…10分
丙丁总分刚好得 18分的情况包含:
事件 A:丙得 12分有 6+6一种情况,丁得 6分有 6+0,0+6,3+3三种情况,
则 ;
事件 B:丙得 9分有 6+3,3+6两种情况,丁得 9分有 6+3,3+6两种情况,
则 ;
事件 C:丙得 6分有 6+0,0+6,3+3三种情况,丁得 12分有 6+6一种情况,
则 ;…………………………………14分
所以丙丁总分刚好得 18分的概率 .…………15分
18.解:(I)由 , ,所以 .
由 平面 ,所以 .
由 , , ,所以平面 平面 .…4分
(II)取 中点 ,连接 ,
在梯形 中,因为 , ,所以 , ,
则在 中, ,由 ,则 ,………………6分
易知 两两垂直,分别以 为 轴,建立空间直角坐标系,
如下图所示:
在四棱柱 中, ,则 ,
因为 平面 , 平面 ,所以 ,
在 中, ,
则 , , , ,
取 , , ,
设平面 的法向量为 ,可得 ,则 ,
取 ,则 ,所以平面 的一个法向量 ,……………8分
设点 到平面 的距离 ,
设直线 与平面 所成角为 ,则 ,即 ,
在四棱柱 中,因为 ,且 平面 ,
所以当直线 与 所成角为 时,其余弦值取得最大值,即为 .……10分
(III)由题意作图如下:由题可知
, , ,
因为 ,所以 ,则 , ,
,
设
平面 的法向量 ,可得 ,
则 ,令 ,则 ,
所以平面 的一个法向量 ,
设平面 的法向量 ,可得 ,
则 ,令 ,则 ,
所以平面 的一个法向量 ,…………………………14分
设二面角 的大小为 ,
则 ,
由二面角 的正弦值为 ,则 ,
可得 ,化简可得 ,解得 或 ,…………16分
由 ,则 ,故存在, .………………17分
19.解:
(I)因为 单调递增,不存在正数 ,使得 恒成立,
所以数列 不具有性质 .………………………………………………………2分
因为 ,又数列 为单调递减数列,所以数列 具有性质 .……4分
(II)因为 ,
若 为奇数的概率为 为偶数的概率为 ,
①………………
………………6分
② ,
……………………………………7分
,即 .………………………………………8分
所以当 时, ,故 随着 的增大而增大,且 .
故数列 具有性质 .……………………………10分
(III)令 ,则 , , ,
所以当 时, 在 上递减,而 ,
故 在 有唯一的零点 ,即 ,即 ………………12分
且当 时, ,即 ,
当 时, ,即
由 ,可知 ,
在 上单调递增;……………………………………………………………13分
由 ,
所以 ,
所以 ,……………………14分
假设 时, 成立,
则 ,即 成立,
结合 可得:对于任意 恒成立,
故 为递增数列, 为递减数列.…………………………………………16分
对数列 ,存在 ,使 ,所以数列 具有性质
对数列 ,存在 ,使 ,所以数列 也具有性质 ……17分
同课章节目录
