人教版数学八年级下册第一次月考(培优)试题(含答案)
文档属性
| 名称 | 人教版数学八年级下册第一次月考(培优)试题(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 132.7KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-01-22 20:25:26 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
人教版数学八年级下册第一次月考(培优)试题
一、单选题
1.(2020八上·会宁期中)在直角 中, ,如果 , ,那么 的长是( )
A.2 B.5 C. D.5或
2.(2022八下·广州期末)( )
A.-2.25 B.-1.5 C.1.5 D.2.25
3.(2023八下·江南期末)下列属于最简二次根式的是( )
A. B. C. D.
4.(2023八上·南岸期中)下列各组数中,是勾股数的是( )
A.6,9,12 B.2,3,4 C.5,12,13 D.,,
5.(2024八上·重庆市月考)一直角三角形的两直角边长分别为9,12,则斜边长为( )
A.13 B.14 C.15 D.20
6.(2019八下·温州期中)下列二次根式中,最简二次根式为( )
A. B. C. D.
7.(2020·拱墅模拟)如图,△ABC中,AB⊥BC,AB=2CB,以C为圆心,CB为半径作弧交AC于点D,以A为圆心,AD长为半径画弧交AB于点E,则 的值是( )
A. B. C. D.
8.(2024九上·深圳月考)已知n是正整数,是整数,则n的最小值是( )
A.0 B.2 C.3 D.7
9.(2024九下·吉林开学考)下列计算正确的是( )
A. B. C. D.
10.(2023九上·开州开学考)如图,在正方形中,点在上,点在的延长线上满足,连接,取的中点,连接,,若,则( )
A. B. C. D.
二、填空题
11.(2020·镇平模拟)计算: .
12.(2022八下·钦南月考)要使二次根式有意义,必须满足 .
13.(2023八下·崇阳月考)若实数,满足,则 .
14.(2019·昌图模拟)已知 ,那么 = .
15.(2019七上·潮安期末)当 取最大值时,方程 的解为 .
16.(2024八下·广州期末)如图,在直角坐标系中,点A的坐标为,以线段为边在第四象限内作等边,点为x轴正半轴上一动点,连接,以线段为边在第四象限内作等边,直线交y轴于点E,则四边形的面积是 .(结果用含a的式子表示)
三、计算题
17.(2023八下·谷城期中)计算下列各题.
(1);
(2)
18.(2024九下·陕西模拟)计算:.
19.(2024八下·新泰月考)(1)若的小数部分为a,5的小数部分为b,求ab
(2)已知a、b、c在数轴上的位置如图所示,化简
四、解答题
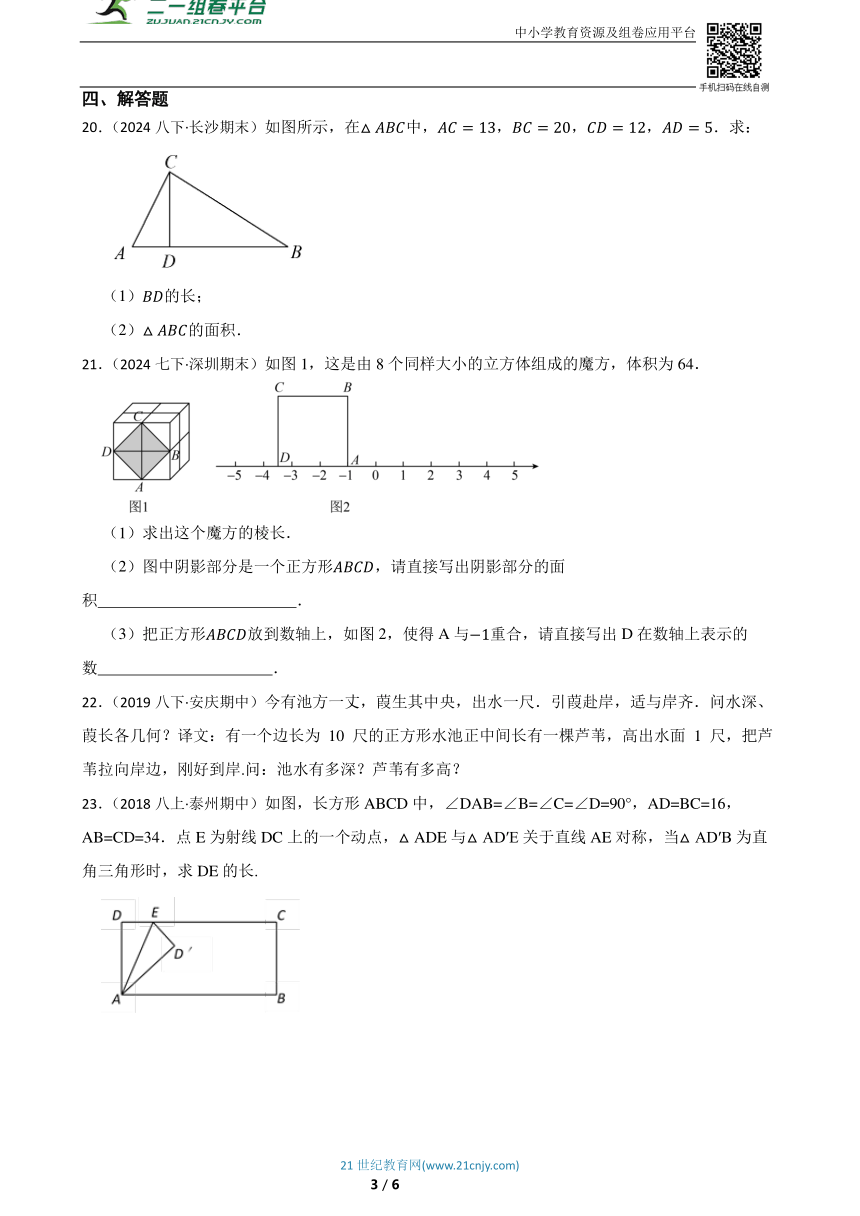
20.(2024八下·长沙期末)如图所示,在中,,,,.求:
(1)的长;
(2)的面积.
21.(2024七下·深圳期末)如图1,这是由8个同样大小的立方体组成的魔方,体积为64.
(1)求出这个魔方的棱长.
(2)图中阴影部分是一个正方形,请直接写出阴影部分的面积 .
(3)把正方形放到数轴上,如图2,使得A与重合,请直接写出D在数轴上表示的数 .
22.(2019八下·安庆期中)今有池方一丈,葭生其中央,出水一尺.引葭赴岸,适与岸齐.问水深、葭长各几何?译文:有一个边长为 10 尺的正方形水池正中间长有一棵芦苇,高出水面 1 尺,把芦苇拉向岸边,刚好到岸.问:池水有多深?芦苇有多高?
23.(2018八上·泰州期中)如图,长方形ABCD中,∠DAB=∠B=∠C=∠D=90°,AD=BC=16,AB=CD=34.点E为射线DC上的一个动点,△ADE与△AD′E关于直线AE对称,当△AD′B为直角三角形时,求DE的长.
答案解析部分
1.【答案】C
【知识点】勾股定理
2.【答案】C
【知识点】二次根式的性质与化简
3.【答案】A
【知识点】最简二次根式
4.【答案】C
【知识点】勾股数
5.【答案】C
【知识点】勾股定理
6.【答案】B
【知识点】最简二次根式
7.【答案】C
【知识点】勾股定理的应用
8.【答案】D
【知识点】二次根式的定义;二次根式的性质与化简
9.【答案】A
【知识点】二次根式的性质与化简;二次根式的乘除法;二次根式的加减法;求算术平方根
10.【答案】B
【知识点】三角形全等及其性质;三角形全等的判定;勾股定理
11.【答案】
【知识点】二次根式的乘除法
12.【答案】
【知识点】分式有无意义的条件;二次根式有意义的条件
13.【答案】
【知识点】负整数指数幂;二次根式有意义的条件;求代数式的值-直接代入求值
14.【答案】-8
【知识点】算术平方根的性质(双重非负性);绝对值的非负性
15.【答案】
【知识点】解一元一次方程;算术平方根的性质(双重非负性)
16.【答案】
【知识点】二次根式的加减法;等边三角形的性质;含30°角的直角三角形;勾股定理
17.【答案】(1)-1;
(2)3+.
【知识点】二次根式的乘除法;二次根式的加减法
18.【答案】
【知识点】负整数指数幂;二次根式的混合运算
19.【答案】(1);(2)
【知识点】无理数的估值;二次根式的混合运算
20.【答案】(1)解:∵
∴
∴
在中,BC=20,CD=12
(2)解:由(1)知:CD⊥AB
∴
【知识点】勾股定理;勾股定理的逆定理
21.【答案】(1)4
(2)8
(3)
【知识点】无理数在数轴上表示;勾股定理;立方根的实际应用
22.【答案】解:设水池深x尺.根据题意得: x2+( )2=( x+1) 2 解得:x=12 x+1=12+1=13. 答:池水有12尺深,芦苇有13尺高.
【知识点】勾股定理的应用
23.【答案】解:如图1.
∵折叠,∴△AD′E≌△ADE,∴∠AD′E=∠D=90°.
∵∠AD′B=90°,∴B、D′、E三点共线.
又∵ABD′∽△BEC,AD′=BC,∴ABD′≌△BEC,∴BE=AB=34.
∵BD′= = =30,∴DE=D′E=34﹣30=4;
如图2.
∵∠ABD″+∠CBE=∠ABD″+∠BAD″=90°,∴∠CBE=∠BAD″.在△ABD″和△BEC中, ,∴△ABD″≌△BEC,∴BE=AB=34,∴DE=D″E=34+30=64.
综上所述:DE=4或64.
故答案为:4或64.
【知识点】全等三角形的判定与性质;勾股定理;轴对称的性质
21世纪教育网(www.21cnjy.com)
1 / 6
人教版数学八年级下册第一次月考(培优)试题
一、单选题
1.(2020八上·会宁期中)在直角 中, ,如果 , ,那么 的长是( )
A.2 B.5 C. D.5或
2.(2022八下·广州期末)( )
A.-2.25 B.-1.5 C.1.5 D.2.25
3.(2023八下·江南期末)下列属于最简二次根式的是( )
A. B. C. D.
4.(2023八上·南岸期中)下列各组数中,是勾股数的是( )
A.6,9,12 B.2,3,4 C.5,12,13 D.,,
5.(2024八上·重庆市月考)一直角三角形的两直角边长分别为9,12,则斜边长为( )
A.13 B.14 C.15 D.20
6.(2019八下·温州期中)下列二次根式中,最简二次根式为( )
A. B. C. D.
7.(2020·拱墅模拟)如图,△ABC中,AB⊥BC,AB=2CB,以C为圆心,CB为半径作弧交AC于点D,以A为圆心,AD长为半径画弧交AB于点E,则 的值是( )
A. B. C. D.
8.(2024九上·深圳月考)已知n是正整数,是整数,则n的最小值是( )
A.0 B.2 C.3 D.7
9.(2024九下·吉林开学考)下列计算正确的是( )
A. B. C. D.
10.(2023九上·开州开学考)如图,在正方形中,点在上,点在的延长线上满足,连接,取的中点,连接,,若,则( )
A. B. C. D.
二、填空题
11.(2020·镇平模拟)计算: .
12.(2022八下·钦南月考)要使二次根式有意义,必须满足 .
13.(2023八下·崇阳月考)若实数,满足,则 .
14.(2019·昌图模拟)已知 ,那么 = .
15.(2019七上·潮安期末)当 取最大值时,方程 的解为 .
16.(2024八下·广州期末)如图,在直角坐标系中,点A的坐标为,以线段为边在第四象限内作等边,点为x轴正半轴上一动点,连接,以线段为边在第四象限内作等边,直线交y轴于点E,则四边形的面积是 .(结果用含a的式子表示)
三、计算题
17.(2023八下·谷城期中)计算下列各题.
(1);
(2)
18.(2024九下·陕西模拟)计算:.
19.(2024八下·新泰月考)(1)若的小数部分为a,5的小数部分为b,求ab
(2)已知a、b、c在数轴上的位置如图所示,化简
四、解答题
20.(2024八下·长沙期末)如图所示,在中,,,,.求:
(1)的长;
(2)的面积.
21.(2024七下·深圳期末)如图1,这是由8个同样大小的立方体组成的魔方,体积为64.
(1)求出这个魔方的棱长.
(2)图中阴影部分是一个正方形,请直接写出阴影部分的面积 .
(3)把正方形放到数轴上,如图2,使得A与重合,请直接写出D在数轴上表示的数 .
22.(2019八下·安庆期中)今有池方一丈,葭生其中央,出水一尺.引葭赴岸,适与岸齐.问水深、葭长各几何?译文:有一个边长为 10 尺的正方形水池正中间长有一棵芦苇,高出水面 1 尺,把芦苇拉向岸边,刚好到岸.问:池水有多深?芦苇有多高?
23.(2018八上·泰州期中)如图,长方形ABCD中,∠DAB=∠B=∠C=∠D=90°,AD=BC=16,AB=CD=34.点E为射线DC上的一个动点,△ADE与△AD′E关于直线AE对称,当△AD′B为直角三角形时,求DE的长.
答案解析部分
1.【答案】C
【知识点】勾股定理
2.【答案】C
【知识点】二次根式的性质与化简
3.【答案】A
【知识点】最简二次根式
4.【答案】C
【知识点】勾股数
5.【答案】C
【知识点】勾股定理
6.【答案】B
【知识点】最简二次根式
7.【答案】C
【知识点】勾股定理的应用
8.【答案】D
【知识点】二次根式的定义;二次根式的性质与化简
9.【答案】A
【知识点】二次根式的性质与化简;二次根式的乘除法;二次根式的加减法;求算术平方根
10.【答案】B
【知识点】三角形全等及其性质;三角形全等的判定;勾股定理
11.【答案】
【知识点】二次根式的乘除法
12.【答案】
【知识点】分式有无意义的条件;二次根式有意义的条件
13.【答案】
【知识点】负整数指数幂;二次根式有意义的条件;求代数式的值-直接代入求值
14.【答案】-8
【知识点】算术平方根的性质(双重非负性);绝对值的非负性
15.【答案】
【知识点】解一元一次方程;算术平方根的性质(双重非负性)
16.【答案】
【知识点】二次根式的加减法;等边三角形的性质;含30°角的直角三角形;勾股定理
17.【答案】(1)-1;
(2)3+.
【知识点】二次根式的乘除法;二次根式的加减法
18.【答案】
【知识点】负整数指数幂;二次根式的混合运算
19.【答案】(1);(2)
【知识点】无理数的估值;二次根式的混合运算
20.【答案】(1)解:∵
∴
∴
在中,BC=20,CD=12
(2)解:由(1)知:CD⊥AB
∴
【知识点】勾股定理;勾股定理的逆定理
21.【答案】(1)4
(2)8
(3)
【知识点】无理数在数轴上表示;勾股定理;立方根的实际应用
22.【答案】解:设水池深x尺.根据题意得: x2+( )2=( x+1) 2 解得:x=12 x+1=12+1=13. 答:池水有12尺深,芦苇有13尺高.
【知识点】勾股定理的应用
23.【答案】解:如图1.
∵折叠,∴△AD′E≌△ADE,∴∠AD′E=∠D=90°.
∵∠AD′B=90°,∴B、D′、E三点共线.
又∵ABD′∽△BEC,AD′=BC,∴ABD′≌△BEC,∴BE=AB=34.
∵BD′= = =30,∴DE=D′E=34﹣30=4;
如图2.
∵∠ABD″+∠CBE=∠ABD″+∠BAD″=90°,∴∠CBE=∠BAD″.在△ABD″和△BEC中, ,∴△ABD″≌△BEC,∴BE=AB=34,∴DE=D″E=34+30=64.
综上所述:DE=4或64.
故答案为:4或64.
【知识点】全等三角形的判定与性质;勾股定理;轴对称的性质
21世纪教育网(www.21cnjy.com)
1 / 6
同课章节目录
