5.1.2 弧度制 课件(共20张PPT)
文档属性
| 名称 | 5.1.2 弧度制 课件(共20张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-01-22 14:15:37 | ||
图片预览







文档简介
(共20张PPT)
5.1.2 弧度制
创设情景
身高:
226cm
司马迁的《孔子世家》里,称:“孔子长九尺有六寸,人皆谓之‘长人’而异之”。
西汉一尺等于23.1厘米
身高:221.76cm
创设情景
度量质量:
磅、千克等
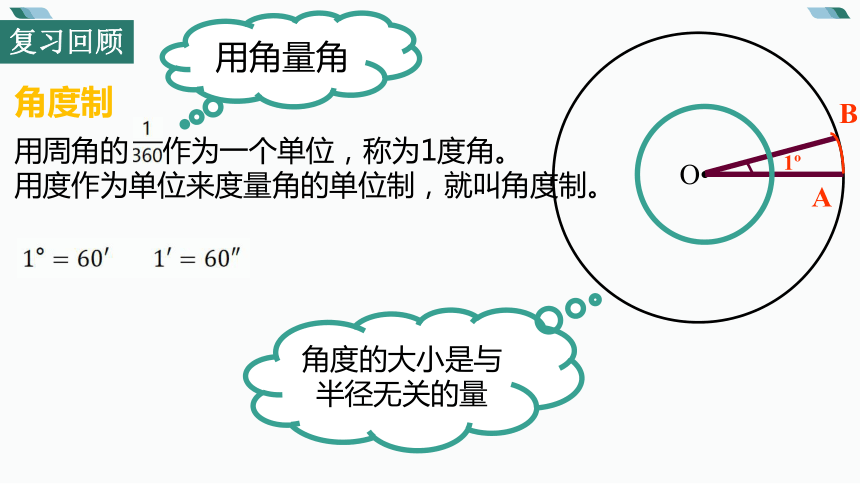
复习回顾
角度制
用周角的 作为一个单位,称为1度角。
用度作为单位来度量角的单位制,就叫角度制。
角度的大小是与半径无关的量
用角量角
O
1
B
A
提出问题
历史上数学家发现这类问题的运算严重影响了数学中三角函数的发展,那么如何才能彻底解决这个问题呢
能否找到一个新的角的度量方式,将角的运算与实数的运算统一起来?
探究活动
圆心角 90° 180° 270° 360°
弧长l
半径r
l/r
活动1:(1)以小组为单位,计算当半径 r=1 和 r=2 时, gvewsghwerb对应的弧长,弧长与半径的比值。
(2)小组讨论,分享你的发现。
探究活动
结论:(1)圆心角所对的弧长与半径的比值,只与的大小有关;
(2)当圆心角确定时,弧长与半径的比值也唯一确定.
问题:能否给这个结论找一个理论支撑呢?
概念生成
我们规定:长度等于半径长的圆弧所对的圆心角叫做1弧度的角,弧度单位用符号表示,读作弧度.
r
r
O
A
B
注:弧度的单位 “rad” 可以省略;
而角度的单位“ °”不可省略
概念生成
几何画板
概念生成
O
A
B
1
1
1 rad
我们把半径为1的圆叫单位圆
问题探究
O
A
B
r
l=r
1 rad
思考:如果弧长是l,半径是r,那么弧所对的圆心角α的弧度数是多少?
O
A
B
r
l=3r
3rad
概念生成a
O
A
B
r
l=2r
思考:如果弧长是l,半径是r,那么弧所对的圆心角α的弧度数是多少?
探究活动
弧度制与角度制的换算
活动二:以小组为单位,共同探讨完成以下问题
(1)已知圆的半径为r(独立完成以下表格):
(2)(小组讨论)得出结论:360°=__________(填弧度数)
180°=__________(填弧度数)
(3)1rad =__________ (填角度数)
1°=_____________(填弧度数)
半径 周长 圆周的弧度数 圆周的角度数
r
概念生成
约定:通常弧度单位可以省略
典例分析
例1 :将下列各角从角度转化为弧度
(1) (2)
例2:将下列各角从弧度转化为角度
(1) (2)
探究活动
活动三:
1、请大家完成一些特殊角的角度数和弧度数的互化
2、请用弧度表示与30°角终边相同角的集合
角度 0° 30° 45° 120° 135° 150° 360°
弧度
探究活动
2、请用弧度表示与30°角终边相同角的集合
注:两种度量制不可混用
归纳小结
(1)两种单位都是度量角的大小的单位制
(2)弧度制是以“弧度”为单位的度量角的单位制(用线段量角),角度制是以“度”为单位度量角的单位制(用角量角)
(3)角度制是六十进制,弧度制是十进制
弧度制与角度制的区别与联系
归纳小结
在弧度制下,角的集合和实数R之间建立一种一一对应关系
弧度制与角度制的区别与联系
任意角的集合
实数集R
一一对应
正角
零角
负角
正实数
0
负实数
本节课你学习了哪些内容?
类比思想
数形结合思想
数学思想:
5.1.2 弧度制
创设情景
身高:
226cm
司马迁的《孔子世家》里,称:“孔子长九尺有六寸,人皆谓之‘长人’而异之”。
西汉一尺等于23.1厘米
身高:221.76cm
创设情景
度量质量:
磅、千克等
复习回顾
角度制
用周角的 作为一个单位,称为1度角。
用度作为单位来度量角的单位制,就叫角度制。
角度的大小是与半径无关的量
用角量角
O
1
B
A
提出问题
历史上数学家发现这类问题的运算严重影响了数学中三角函数的发展,那么如何才能彻底解决这个问题呢
能否找到一个新的角的度量方式,将角的运算与实数的运算统一起来?
探究活动
圆心角 90° 180° 270° 360°
弧长l
半径r
l/r
活动1:(1)以小组为单位,计算当半径 r=1 和 r=2 时, gvewsghwerb对应的弧长,弧长与半径的比值。
(2)小组讨论,分享你的发现。
探究活动
结论:(1)圆心角所对的弧长与半径的比值,只与的大小有关;
(2)当圆心角确定时,弧长与半径的比值也唯一确定.
问题:能否给这个结论找一个理论支撑呢?
概念生成
我们规定:长度等于半径长的圆弧所对的圆心角叫做1弧度的角,弧度单位用符号表示,读作弧度.
r
r
O
A
B
注:弧度的单位 “rad” 可以省略;
而角度的单位“ °”不可省略
概念生成
几何画板
概念生成
O
A
B
1
1
1 rad
我们把半径为1的圆叫单位圆
问题探究
O
A
B
r
l=r
1 rad
思考:如果弧长是l,半径是r,那么弧所对的圆心角α的弧度数是多少?
O
A
B
r
l=3r
3rad
概念生成a
O
A
B
r
l=2r
思考:如果弧长是l,半径是r,那么弧所对的圆心角α的弧度数是多少?
探究活动
弧度制与角度制的换算
活动二:以小组为单位,共同探讨完成以下问题
(1)已知圆的半径为r(独立完成以下表格):
(2)(小组讨论)得出结论:360°=__________(填弧度数)
180°=__________(填弧度数)
(3)1rad =__________ (填角度数)
1°=_____________(填弧度数)
半径 周长 圆周的弧度数 圆周的角度数
r
概念生成
约定:通常弧度单位可以省略
典例分析
例1 :将下列各角从角度转化为弧度
(1) (2)
例2:将下列各角从弧度转化为角度
(1) (2)
探究活动
活动三:
1、请大家完成一些特殊角的角度数和弧度数的互化
2、请用弧度表示与30°角终边相同角的集合
角度 0° 30° 45° 120° 135° 150° 360°
弧度
探究活动
2、请用弧度表示与30°角终边相同角的集合
注:两种度量制不可混用
归纳小结
(1)两种单位都是度量角的大小的单位制
(2)弧度制是以“弧度”为单位的度量角的单位制(用线段量角),角度制是以“度”为单位度量角的单位制(用角量角)
(3)角度制是六十进制,弧度制是十进制
弧度制与角度制的区别与联系
归纳小结
在弧度制下,角的集合和实数R之间建立一种一一对应关系
弧度制与角度制的区别与联系
任意角的集合
实数集R
一一对应
正角
零角
负角
正实数
0
负实数
本节课你学习了哪些内容?
类比思想
数形结合思想
数学思想:
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
