2025年中考数学第一轮提升练习—— 一次函数(含答案)
文档属性
| 名称 | 2025年中考数学第一轮提升练习—— 一次函数(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 214.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-01-24 00:00:00 | ||
图片预览

文档简介
中考数学第一轮提升练习——一次函数
一、单选题
1.在函数 中,自变量 的取值范围是( )
A. B. C. D.
2.已知一次函数,若随的增大而减小,则它的图象经过( )
A.第一、二、三象限 B.第一、二、四象限
C.第二、三、四象限 D.第一、三、四象限
3.实数k、b满足kb﹥0,不等式kxA. B.
C. D.
4.如图,函数y=2x和y=ax+4的图象相交于点A(m,3),则不等式2x≥ax+4的解集为( )
A.x≥ B.x≤3 C.x≤ D.x≥3
5.如图,在平面直角坐标系中,直线y=- x+3与矩形OABC的边AB、BC分别交于点E、F,若点B的坐标为(m,2),则m的值可能为( )
A. B. C. D.
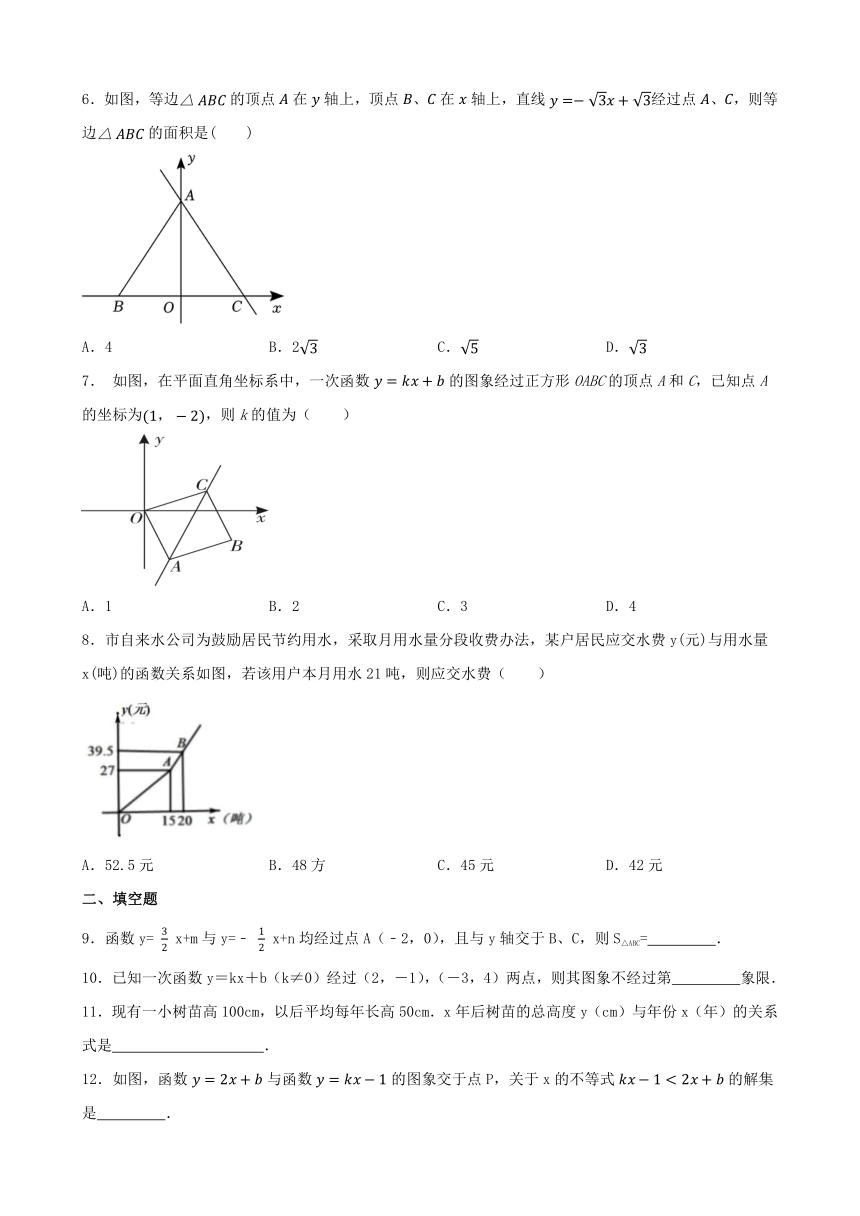
6.如图,等边的顶点在轴上,顶点、在轴上,直线经过点、,则等边的面积是( )
A.4 B.2 C. D.
7. 如图,在平面直角坐标系中,一次函数的图象经过正方形OABC的顶点A和C,已知点A的坐标为,则k的值为( )
A.1 B.2 C.3 D.4
8.市自来水公司为鼓励居民节约用水,采取月用水量分段收费办法,某户居民应交水费y(元)与用水量x(吨)的函数关系如图,若该用户本月用水21吨,则应交水费( )
A.52.5元 B.48方 C.45元 D.42元
二、填空题
9.函数y= x+m与y=﹣ x+n均经过点A(﹣2,0),且与y轴交于B、C,则S△ABC= .
10.已知一次函数y=kx+b(k≠0)经过(2,-1),(-3,4)两点,则其图象不经过第 象限.
11.现有一小树苗高100cm,以后平均每年长高50cm.x年后树苗的总高度y(cm)与年份x(年)的关系式是 .
12.如图,函数与函数的图象交于点P,关于x的不等式的解集是 .
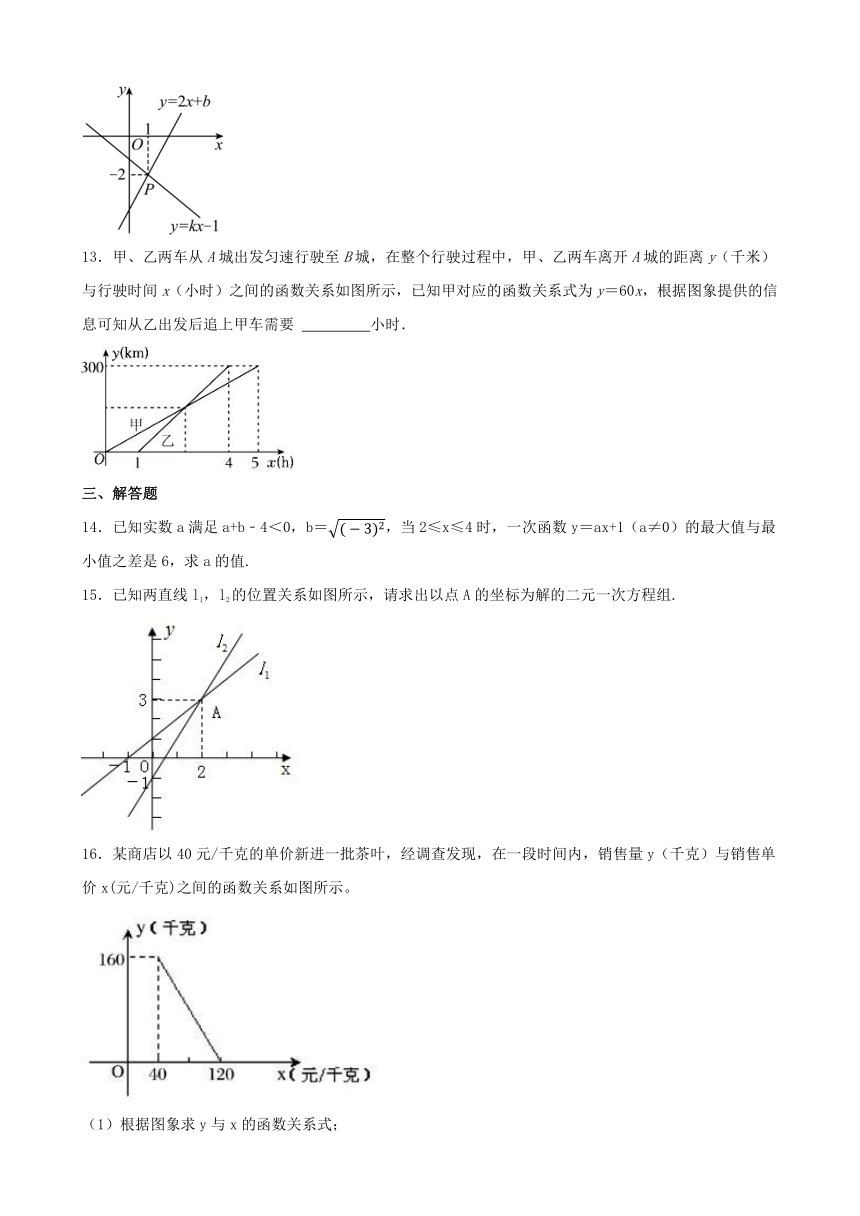
13.甲、乙两车从A城出发匀速行驶至B城,在整个行驶过程中,甲、乙两车离开A城的距离y(千米)与行驶时间x(小时)之间的函数关系如图所示,已知甲对应的函数关系式为y=60x,根据图象提供的信息可知从乙出发后追上甲车需要 小时.
三、解答题
14.已知实数a满足a+b﹣4<0,b=,当2≤x≤4时,一次函数y=ax+1(a≠0)的最大值与最小值之差是6,求a的值.
15.已知两直线l1,l2的位置关系如图所示,请求出以点A的坐标为解的二元一次方程组.
16.某商店以40元/千克的单价新进一批茶叶,经调查发现,在一段时间内,销售量y(千克)与销售单价x(元/千克)之间的函数关系如图所示。
(1)根据图象求y与x的函数关系式;
(2)商店想在销售成本不超过3000元的情况下,使销售利润达到2400元,销售单价应定为多少
17.五月份正是杏大量上市的季节,小李将自家产的杏拿到集市上售卖,小李在卖杏之前,钱包内有零钱元,下表记录的是杏的销售额(元)随销售量(千克)变化的有关数据:
销量(千克)
销售额(元)
请根据表中数据回答下列问题:
(1)直接写出,值;
(2)求在小李售卖杏的过程中,钱包里的零钱(元)与(千克)的函数关系式;
(3)求销量为18千克时小李钱包中的零钱.
18.如图10,在平面直角坐标系内,已知直线,l1经过原点O及A(2,2 )两点,将直线l1向右平移4个单位后得到直线l2,直线l2与X轴交于点B.
(1)求直线l2的函数表达式;
(2)作∠AOB的平分线交直线l2于点C,连接AC.求证:四边形 ACB是菱形;
(3)设点P是直线l2于一点,以P为圆心,PB为半径作⊙P,当⊙P与直线l1相切时,请求出圆心P点的坐标.
答案
1.A
2.C
3.B
4.A
5.B
6.D
7.C
8.D
9.4
10.三
11.y=50x+100(x≥0)
12.
13.1.5
14.解:∵b==3,a+b﹣4<0,
∴a<1,
①当a<0时,(2a+1)﹣(4a+1)=6,
解得:a=﹣3;
②当0<a<1时,(4a+1)﹣(2a+1)=6,
解得:a=3(舍去),
综上,a=﹣3.
15.解:设直线l1的解析式是y=kx+b,已知直线l1经过(-1,0)和(2,3),根据题意,得: ,
解得 ;
则直线l1的函数解析式是y=x+1;
同理得直线l2的函数解析式是y=2x-1.
则所求的方程组是 ;
两个函数图象的交点坐标为A(2,3)
16.(1)解:设y与x函数关系式为y=kx+b,把点(40,160),(120,0)代入得,
解得
.y与x函数关系式为y=-2x+240(40≤x≤120)
(2)解:由题意,销售成本不超过3000元,AP(千克)
得40(-2x+240)≤3000.
解不等式得,x≥82.5.
∴82.5≤x≤120.
根据题意列方程得(x-40)(一2x+240)=2400.
即:x2-160x+6000=0.
解得x1=60,x2=100.
∵60<82.5,故舍去.
销售单价应该定为100元
17.(1)解:,
(2)解:小李在卖杏之前,钱包内有零钱元,观察表中数据可知,销量每增加千克,销售额就增加元,
(3)解:当时,
.
销量为千克时小李钱包中的零钱为元.
18.(1)解:由题意可设l1的函数表示式为y=kx,将A(2,2 )代入可得2k=2 ,解得k= ,
∴l1的函数表示式为y= x,
∵将直线l1向右平移4个单位后得到直线l2,
∴l2的函数表示式为y= (x-4)= x-4 .
(2)证明:由平移的性质可得l1// l2,
所以∠AOC=∠OCB,
因为OC平分∠AOB,
所以∠AOC=∠BOC,
所以∠BOC=∠OCB,
所以BC=OB=4,
由A(2,2 )可得OA= ,
所以OA=OB=BC,
则四边形OACB是菱形.
(3)解:过点A作AD⊥OB,垂足为D,由A(2,2 )可得AD=2 ,因为OACB是菱形,所以点B到OA距离等于AD=2 .由点P到OA的距离为2 ,所以当⊙P的半径为2 时,直线l1与⊙P相切,则PB=AD=2 ,
因为点P在直线l2,所以可设P(x, x-4 ),又因为B(4,0),
则PB2=(x-4)2+( x-4 )2=(2 )2,化简得(x-4)2=3,解得x=4± ,则P(4+ ,3)或(4- ,-3)
一、单选题
1.在函数 中,自变量 的取值范围是( )
A. B. C. D.
2.已知一次函数,若随的增大而减小,则它的图象经过( )
A.第一、二、三象限 B.第一、二、四象限
C.第二、三、四象限 D.第一、三、四象限
3.实数k、b满足kb﹥0,不等式kx
C. D.
4.如图,函数y=2x和y=ax+4的图象相交于点A(m,3),则不等式2x≥ax+4的解集为( )
A.x≥ B.x≤3 C.x≤ D.x≥3
5.如图,在平面直角坐标系中,直线y=- x+3与矩形OABC的边AB、BC分别交于点E、F,若点B的坐标为(m,2),则m的值可能为( )
A. B. C. D.
6.如图,等边的顶点在轴上,顶点、在轴上,直线经过点、,则等边的面积是( )
A.4 B.2 C. D.
7. 如图,在平面直角坐标系中,一次函数的图象经过正方形OABC的顶点A和C,已知点A的坐标为,则k的值为( )
A.1 B.2 C.3 D.4
8.市自来水公司为鼓励居民节约用水,采取月用水量分段收费办法,某户居民应交水费y(元)与用水量x(吨)的函数关系如图,若该用户本月用水21吨,则应交水费( )
A.52.5元 B.48方 C.45元 D.42元
二、填空题
9.函数y= x+m与y=﹣ x+n均经过点A(﹣2,0),且与y轴交于B、C,则S△ABC= .
10.已知一次函数y=kx+b(k≠0)经过(2,-1),(-3,4)两点,则其图象不经过第 象限.
11.现有一小树苗高100cm,以后平均每年长高50cm.x年后树苗的总高度y(cm)与年份x(年)的关系式是 .
12.如图,函数与函数的图象交于点P,关于x的不等式的解集是 .
13.甲、乙两车从A城出发匀速行驶至B城,在整个行驶过程中,甲、乙两车离开A城的距离y(千米)与行驶时间x(小时)之间的函数关系如图所示,已知甲对应的函数关系式为y=60x,根据图象提供的信息可知从乙出发后追上甲车需要 小时.
三、解答题
14.已知实数a满足a+b﹣4<0,b=,当2≤x≤4时,一次函数y=ax+1(a≠0)的最大值与最小值之差是6,求a的值.
15.已知两直线l1,l2的位置关系如图所示,请求出以点A的坐标为解的二元一次方程组.
16.某商店以40元/千克的单价新进一批茶叶,经调查发现,在一段时间内,销售量y(千克)与销售单价x(元/千克)之间的函数关系如图所示。
(1)根据图象求y与x的函数关系式;
(2)商店想在销售成本不超过3000元的情况下,使销售利润达到2400元,销售单价应定为多少
17.五月份正是杏大量上市的季节,小李将自家产的杏拿到集市上售卖,小李在卖杏之前,钱包内有零钱元,下表记录的是杏的销售额(元)随销售量(千克)变化的有关数据:
销量(千克)
销售额(元)
请根据表中数据回答下列问题:
(1)直接写出,值;
(2)求在小李售卖杏的过程中,钱包里的零钱(元)与(千克)的函数关系式;
(3)求销量为18千克时小李钱包中的零钱.
18.如图10,在平面直角坐标系内,已知直线,l1经过原点O及A(2,2 )两点,将直线l1向右平移4个单位后得到直线l2,直线l2与X轴交于点B.
(1)求直线l2的函数表达式;
(2)作∠AOB的平分线交直线l2于点C,连接AC.求证:四边形 ACB是菱形;
(3)设点P是直线l2于一点,以P为圆心,PB为半径作⊙P,当⊙P与直线l1相切时,请求出圆心P点的坐标.
答案
1.A
2.C
3.B
4.A
5.B
6.D
7.C
8.D
9.4
10.三
11.y=50x+100(x≥0)
12.
13.1.5
14.解:∵b==3,a+b﹣4<0,
∴a<1,
①当a<0时,(2a+1)﹣(4a+1)=6,
解得:a=﹣3;
②当0<a<1时,(4a+1)﹣(2a+1)=6,
解得:a=3(舍去),
综上,a=﹣3.
15.解:设直线l1的解析式是y=kx+b,已知直线l1经过(-1,0)和(2,3),根据题意,得: ,
解得 ;
则直线l1的函数解析式是y=x+1;
同理得直线l2的函数解析式是y=2x-1.
则所求的方程组是 ;
两个函数图象的交点坐标为A(2,3)
16.(1)解:设y与x函数关系式为y=kx+b,把点(40,160),(120,0)代入得,
解得
.y与x函数关系式为y=-2x+240(40≤x≤120)
(2)解:由题意,销售成本不超过3000元,AP(千克)
得40(-2x+240)≤3000.
解不等式得,x≥82.5.
∴82.5≤x≤120.
根据题意列方程得(x-40)(一2x+240)=2400.
即:x2-160x+6000=0.
解得x1=60,x2=100.
∵60<82.5,故舍去.
销售单价应该定为100元
17.(1)解:,
(2)解:小李在卖杏之前,钱包内有零钱元,观察表中数据可知,销量每增加千克,销售额就增加元,
(3)解:当时,
.
销量为千克时小李钱包中的零钱为元.
18.(1)解:由题意可设l1的函数表示式为y=kx,将A(2,2 )代入可得2k=2 ,解得k= ,
∴l1的函数表示式为y= x,
∵将直线l1向右平移4个单位后得到直线l2,
∴l2的函数表示式为y= (x-4)= x-4 .
(2)证明:由平移的性质可得l1// l2,
所以∠AOC=∠OCB,
因为OC平分∠AOB,
所以∠AOC=∠BOC,
所以∠BOC=∠OCB,
所以BC=OB=4,
由A(2,2 )可得OA= ,
所以OA=OB=BC,
则四边形OACB是菱形.
(3)解:过点A作AD⊥OB,垂足为D,由A(2,2 )可得AD=2 ,因为OACB是菱形,所以点B到OA距离等于AD=2 .由点P到OA的距离为2 ,所以当⊙P的半径为2 时,直线l1与⊙P相切,则PB=AD=2 ,
因为点P在直线l2,所以可设P(x, x-4 ),又因为B(4,0),
则PB2=(x-4)2+( x-4 )2=(2 )2,化简得(x-4)2=3,解得x=4± ,则P(4+ ,3)或(4- ,-3)
同课章节目录
