1.1等腰三角形（含答案）

中小学教育资源及组卷应用平台
1等腰三角形
一、单选题
1．如图，在中，，的垂直平分线l交于点M，，则的度数为（　　）
A． B． C． D．
2．如图所示，△ABC是等边三角形，点D在AC边上，∠DBC＝35°，则∠ADB的度数为（　　）
A．25° B．60° C．85° D．95°
3．如图，在中，，D为的中点，连接，则的度数为（　　）
A．55° B．20° C．25° D．40°
4．已知等腰三角形的底边长为4，腰长为9，则它的周长为（　　）
A．13 B．17 C．22 D．17或22
5．如图，△ABC中，AB＝AC，AD是∠BAC的平分线．已知AB＝5，AD＝3，则BC的长为（　　）
A．5 B．6 C．8 D．10
二、填空题
6．如图，，点P在的边上，以点P为圆心，为半径画弧，交于点A，连接，则　 　．
7．已知等边三角形的边长为，则它的面积为　 　．
8．如图，在中，，，于点，的垂直平分线交于点，交于点，连接，则的度数为　 　．
9．如图，“三等分角器”是由两根有槽的棒PA，PB组成，两根棒在P点相连，并可绕点P转动，C点固定，O，A可在槽内滑动，，若，则的度数为　 　°．
10．如图，一艘轮船由海平面上C地出发向南偏西的方向行驶120海里到达B地，再由B地向北偏西的方向行驶120海里到达A地，则A，C两地相距 　 　海里．
11．如图，点，分别在等边三角形的边，上，将沿直线翻折，使点落在处．若，则　 　．
三、计算题
12．如图，在等边中，，点分别从点同时出发，沿三角形的边运动，当点第一次返回到达点时，同时停止运动．已知点的速度是，点的速度是．设点的运动时间为．
（1）当为何值时，两点重合？
（2）当为何值时，为等边三角形？
（3）当点在边上运动时，是否存在时间，使得是以为底边的等腰三角形，若存在，直接写出的值；若不存在，请说明理由．
13．如图，等腰三角形中，，，动点从点出发，沿路线匀速运动，速度为，运动到点停止，设运动时间为，的面积为．
（1）求的面积．
（2）求等腰腰上的高．
（3）请分别求出在边、上运动时，的面积为与运动时间之间的函数关系式．
（4）是否存在某一时刻，使得的面积正好是面积的，若存在，求出的值；若不存在，说明理由．
（5）当运动时间为_______时，（直接填空）为直角三角形．
14．如图，直线交轴于点，交轴于点，点在轴负半轴上，，过点作于点，交轴于点．
（1）请直接写出点，，坐标，______，______，______；
（2）连接，则______，______；
（3）连接，作交于，求______，______．
四、解答题
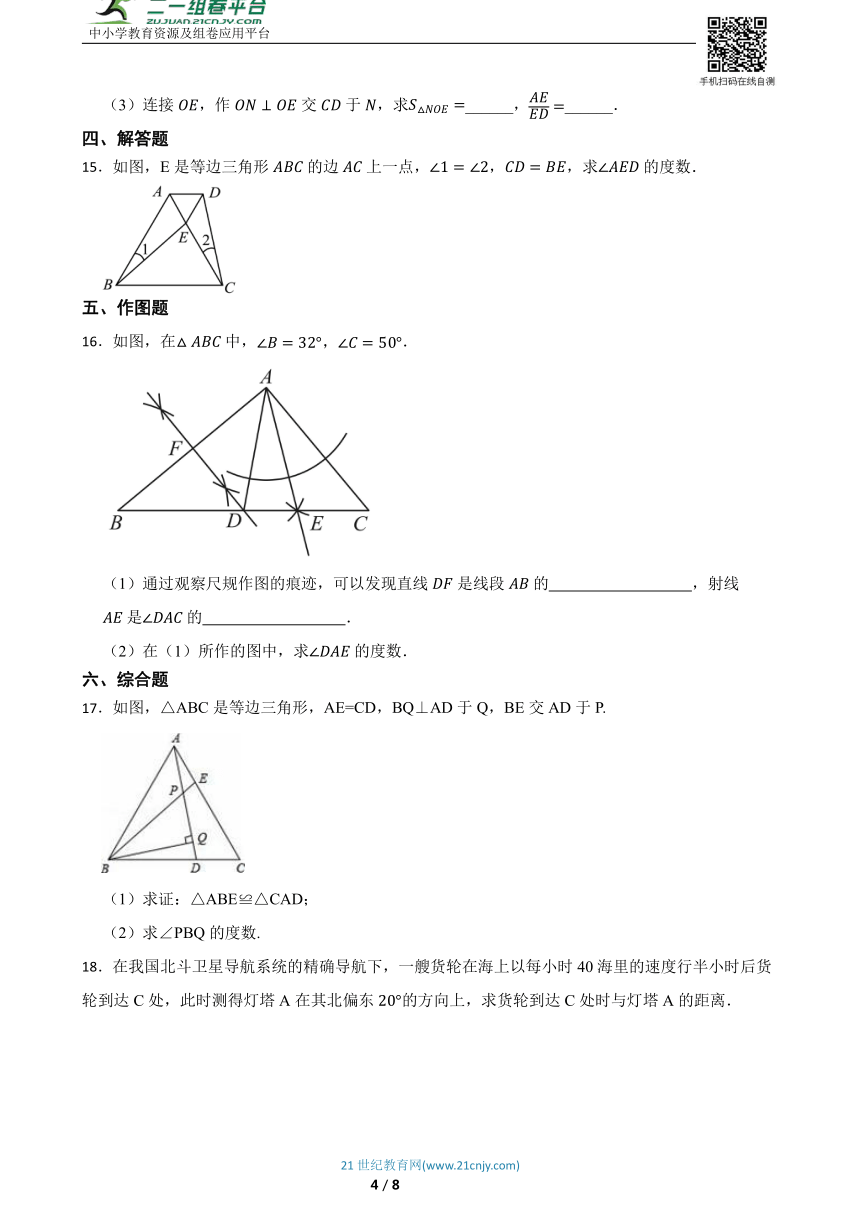
15．如图，E是等边三角形的边上一点，，，求的度数．
五、作图题
16．如图，在中，．
（1）通过观察尺规作图的痕迹，可以发现直线是线段的 ，射线
是的 ．
（2）在（1）所作的图中，求的度数．
六、综合题
17．如图，△ABC是等边三角形，AE=CD，BQ⊥AD于Q，BE交AD于P.
（1）求证：△ABE≌△CAD；
（2）求∠PBQ的度数.
18．在我国北斗卫星导航系统的精确导航下，一艘货轮在海上以每小时40海里的速度行半小时后货轮到达C处，此时测得灯塔A在其北偏东的方向上，求货轮到达C处时与灯塔A的距离．
19．已知：如图，等边三角形ABC中，D、E分别是BC、AC上的点，且AE=CD，
（1）求证：AD=BE
（2）求：∠BFD的度数.
答案解析部分
1．【答案】B
【知识点】三角形的外角性质；线段垂直平分线的性质；等腰三角形的性质
2．【答案】D
【知识点】三角形的外角性质；等边三角形的性质
3．【答案】B
【知识点】等腰三角形的判定与性质
4．【答案】C
【知识点】等腰三角形的性质
5．【答案】C
【知识点】等腰三角形的性质；勾股定理
6．【答案】70
【知识点】三角形的外角性质；等腰三角形的性质
7．【答案】
【知识点】等边三角形的性质；勾股定理
8．【答案】
【知识点】三角形内角和定理；线段垂直平分线的性质；等腰三角形的性质
9．【答案】20
【知识点】三角形的外角性质；等腰三角形的性质
10．【答案】120
【知识点】等边三角形的判定与性质；方位角
11．【答案】
【知识点】三角形内角和定理；等边三角形的性质
12．【答案】（1）当t的值为8时，两点重合
（2）点N运动后，为等边三角形
（3）存在，
【知识点】等腰三角形的判定与性质；等边三角形的判定与性质；三角形全等的判定-SAS
13．【答案】（1）
（2）等腰腰上的高为；
（3）
（4）满足条件的或；
（5）或8
【知识点】函数解析式；等腰三角形的判定与性质；勾股定理
14．【答案】（1），，
（2），
（3），
【知识点】二次根式的混合运算；等腰三角形的判定与性质；勾股定理；一次函数的实际应用-几何问题
15．【答案】
【知识点】等边三角形的判定与性质；三角形全等的判定-SAS
16．【答案】（1）垂直平分线；平分线
（2）
【知识点】线段垂直平分线的性质；等腰三角形的性质；尺规作图-作角的平分线；尺规作图-垂直平分线
17．【答案】（1）证明：∵△ABC是等边三角形，
∴AB=AC，∠BAC=∠C=60°，
在△ABE与△CAD中，
∴△ABE≌△CAD（SAS）；
（2）解：由（1）知△ABE≌△CAD，
∴∠ABE=∠CAD，
∴∠BPQ=∠ABE+∠BAP=∠CAD+∠BAP=∠BAC=60°.
∴∠PBQ=90°-∠BPQ=30°.
【知识点】等边三角形的性质；三角形全等的判定-SAS
18．【答案】货轮到达处时与灯塔的距离是20海里．
【知识点】等边三角形的判定与性质
19．【答案】（1）证明：∵△ABC是等边三角形，
∴∠BAC=∠C=60°，AB=CA，
在△ABE和△CAD中 ，
∴△ABE≌△CAD(SAS)，
∴AD=BE(全等三角形对应边相等)；
（2）解：∵△ABE≌△CAD(已证)，
∴∠ABE=∠CAD(全等三角形对应角相等)，
又∵∠BFD=∠BAD+∠ABE，
∴∠BFD=∠BAD+∠CAD=∠BAC，
又∠BAC=60°，
∴∠BFD=60°.
【知识点】全等三角形的判定与性质；等边三角形的性质
21世纪教育网(www.21cnjy.com)
1 / 8