1.4角平分线

中小学教育资源及组卷应用平台
4角平分线
一、单选题
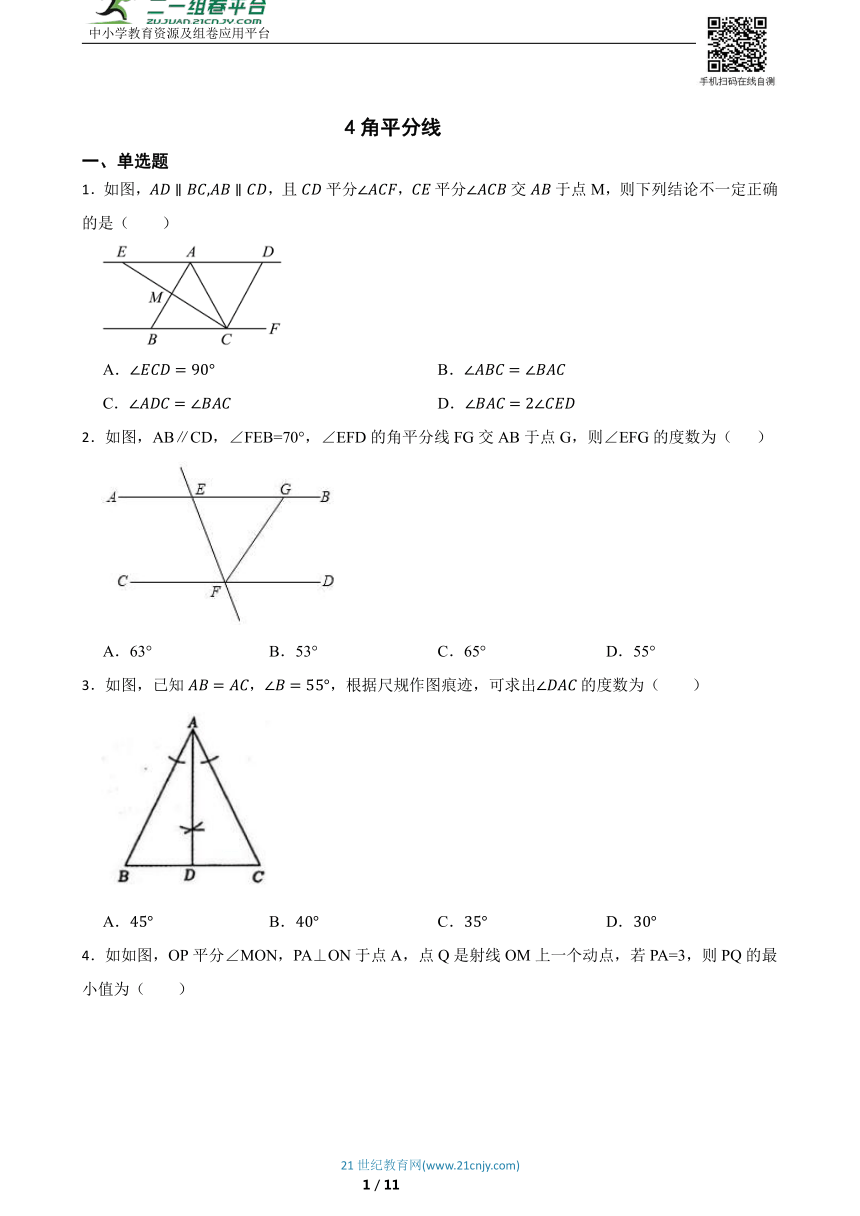
1．如图，，且平分，平分交于点M，则下列结论不一定正确的是（　　）
A． B．
C． D．
2．如图，AB∥CD，∠FEB=70°，∠EFD的角平分线FG交AB于点G，则∠EFG的度数为（ ）
A．63° B．53° C．65° D．55°
3．如图，已知，，根据尺规作图痕迹，可求出的度数为（　　）
A． B． C． D．
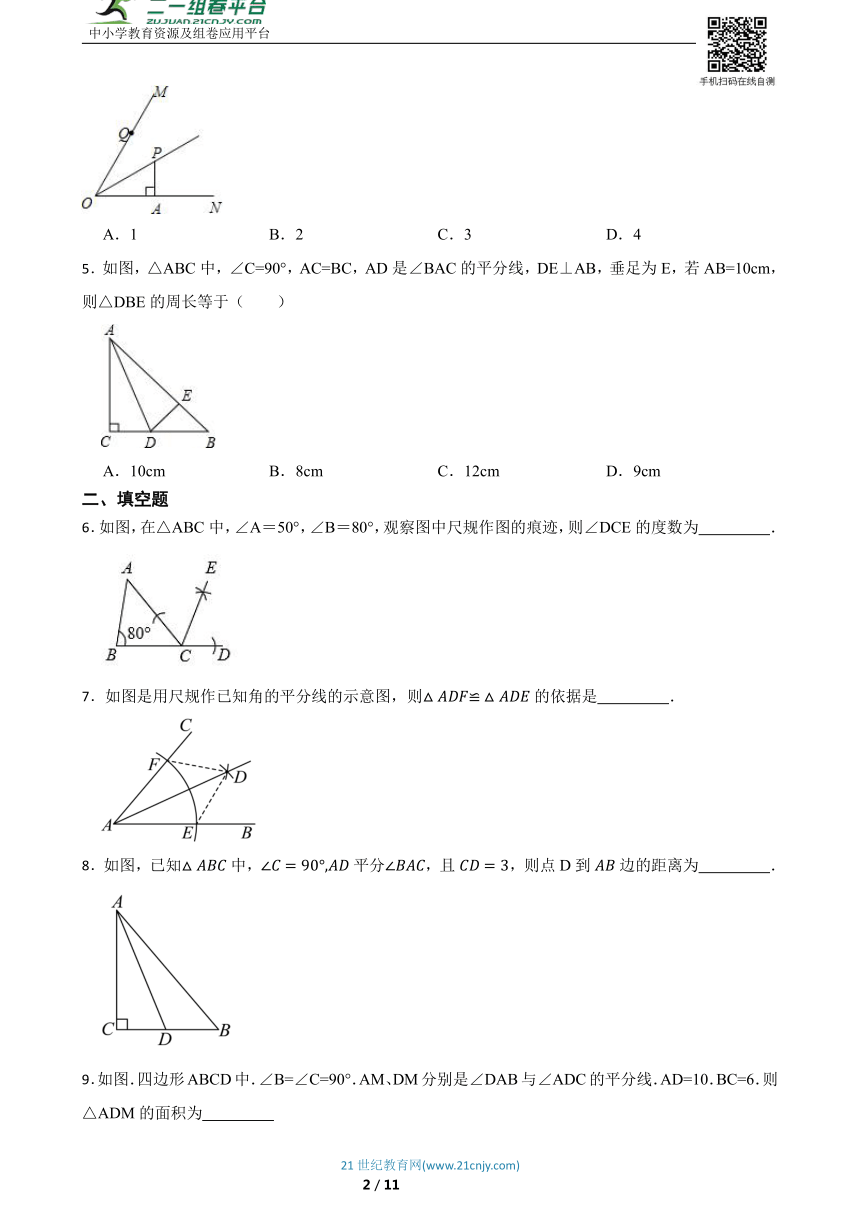
4．如如图，OP平分∠MON，PA⊥ON于点A，点Q是射线OM上一个动点，若PA=3，则PQ的最小值为（　　）
A．1 B．2 C．3 D．4
5．如图，△ABC中，∠C=90°，AC=BC，AD是∠BAC的平分线，DE⊥AB，垂足为E，若AB=10cm，则△DBE的周长等于（　　）
A．10cm B．8cm C．12cm D．9cm
二、填空题
6．如图，在△ABC中，∠A＝50°，∠B＝80°，观察图中尺规作图的痕迹，则∠DCE的度数为　 　．
7．如图是用尺规作已知角的平分线的示意图，则的依据是　 　．
8．如图，已知中，平分，且，则点D到边的距离为　 　．
9．如图．四边形ABCD中．∠B=∠C=90°．AM、DM分别是∠DAB与∠ADC的平分线．AD=10．BC=6．则△ADM的面积为　 　
10．如图，射线是的角平分线，D是射线上一点，于点P，，若点Q是射线上一点，，则的面积是　 　．
11．如图，已知△ABC的面积为20，AB=AC=8，点D为BC边上任一点，过D作DE⊥AB于点E．作DF⊥AC于点F，则DE+DF=　 　．
三、计算题
12．如图． 平分 ， ，垂足为E， 交 的延长线于点F，若 恰好平分 ．求证：

（1）点D为 的中点；
（2） ．
13．已知，，按如图1所示摆放，将OA、OC边重合在直线MN上，OB、OD边在直线MN的两侧；
(1)保持不动，将绕点O旋转至如图2所示的位置，则①= ；②= ；
(2)若按每分钟的速度绕点O逆时针方向旋转，按每分钟的速度也绕点O逆时针方向旋转，OC旋转到射线ON上时都停止运动，设旋转t分钟，计算(用t的代数式表示)。
(3)保持不动，将绕点O逆时针方向旋转，若射线OE平分，射线OF平分，求的大小；
14．综合与实践
问题情境
在数学活动课上，老师和同学们以“线段与角的共性”为主题开展数学活动．发现线段的中点的概念与角的平分线的概念类似，甚至它们在计算的方法上也有类似之处，它们之间的题目可以转换，解法可以互相借鉴．如图1，点是线段上的一点，是的中点，是的中点．
图1 图2 图3
（1）问题探究
①若，，求的长度；（写出计算过程）
②若，，则___________；（直接写出结果）
（2）继续探究
“创新”小组的同学类比想到：如图2，已知，在角的内部作射线，再分别作和的角平分线，．
③若，求的度数；（写出计算过程）
④若，则_____________；（直接写出结果）
（3）深入探究
“慎密”小组在“创新”小组的基础上提出：如图3，若，在角的外部作射线，再分别作和的角平分线，，若，则__________．（直接写出结果）
四、解答题
15．如图，直线，相交于，射线平分，若，求的度数．
五、作图题
16．求作一点P，使点P到∠A两边的距离相等，且点P到点D和点E的距离相等．（保留作图痕迹）
六、综合题
17．如图，直线AB、CD相交于点O，∠BOC＝80°，OE是∠BOC的角平分线，OF是OE的反向延长线．
（1）求∠2、∠3的度数；
（2）说明OF平分∠AOD的理由．
18．如图，如图，已知等腰 ABC 中， AC= AB，BD是 ∠ABC 的角平分线.
（1）尺规作图：作出∠ ACB的角平分线，交 AB 于点E ， 交BD于点F (不写作法，保留作图痕迹)
（2）试判断 △BFC 的形状，并说明理由.
19．如图，已知：AB=AD，BC=CD，AE⊥BC，垂足为E，AF⊥CD，垂足为F．
求证：
（1）∠B=∠D；
（2）AE=AF．
七、实践探究题
20．如图①，OP是∠MON的平分线，请你利用该图形画一对以OP所在直线为对称轴的全等三角形。请你参考这个作全等三角形的方法，解答下列问题：
（1）如图②，在△ABC中，∠ACB是直角，，AD．CE分别是∠BAC、∠BCA的平分线，AD、CE相交于点F。请你判断并写出FE与FD之间的数量关系；
（2）如图③，在△ABC中，如果∠ACB不是直角，而（1）中的其它条件不变，请问，你在（1）中所得结论是否仍然成立？若成立，请证明；若不成立，请说明理由。
答案解析部分
1．【答案】D
【知识点】角平分线的性质；内错角的概念
2．【答案】D
【知识点】角平分线的性质；同旁内角的概念
3．【答案】C
【知识点】等腰三角形的性质；尺规作图-作角的平分线；直角三角形的两锐角互余
4．【答案】C
【知识点】垂线段最短及其应用；角平分线的性质
5．【答案】A
【知识点】角平分线的性质；勾股定理的应用
6．【答案】65°
【知识点】三角形的外角性质；角平分线的性质；尺规作图-作角的平分线
7．【答案】
【知识点】尺规作图-作角的平分线
8．【答案】3
【知识点】角平分线的性质
9．【答案】15
【知识点】三角形的面积；角平分线的性质
10．【答案】10
【知识点】角平分线的性质
11．【答案】5
【知识点】三角形的面积；角平分线的性质
12．【答案】（1）解：如图，过点D作DH⊥AB于H，
∵AD平分∠BAC，DE⊥AC，DH⊥AB，
∴DE=DH，
∵BF∥AC，DE⊥AC，
∴BF⊥DF，
∵BC平分∠ABF，DH⊥AB，DF⊥BF，
∴DF=DH，
∴DE=DF，
∴点D为EF的中点；
（2）解：∵BF∥AC，
∴∠C=∠DBF，
∵∠C=∠DBF，∠CDE=∠BDF，DE=DF，
∴△DCE≌△DBF，
∴CD=BD，
∵BC平分∠ABF，
∴∠ABD=∠DBF，
∴∠C=∠ABD，
∴AC=AB，且CD=BD，
∴AD⊥BC；
【知识点】角平分线的性质；等腰三角形的性质；三角形全等的判定-AAS
13．【答案】(1)①150°；②30°；(2) 8t－60或2t+60；(3) ∠EOF的大小为15°或165°.
【知识点】角的运算；角平分线的性质
14．【答案】（1）①3；②；（2）③40；④40；（3）
【知识点】角平分线的性质；线段的和、差、倍、分的简单计算
15．【答案】．
【知识点】角平分线的性质；对顶角及其性质；邻补角
16．【答案】解：如图，点P即为所求.
【知识点】角平分线的性质；线段垂直平分线的性质；尺规作图-作角的平分线；尺规作图-垂直平分线
17．【答案】（1）解：∵∠BOC+∠2=180°，∠BOC=80°，
∴∠2=180°﹣80°=100°；
∵OE是∠BOC的角平分线，
∴∠1=40°．
∵∠1+∠2+∠3=180°，
∴∠3=180°﹣∠1﹣∠2=180°﹣40°﹣100°=40° 。
（2）解：∵∠2+∠3+∠AOF=180°，
∴∠AOF=180°﹣∠2﹣∠3=180°﹣100°﹣40°=40°，
∴∠AOF=∠3=40°，
∴OF平分∠AOD 。
【知识点】角的运算；角平分线的判定；角平分线的概念
18．【答案】（1）证明：（1）作图
∴如图所示，CE为所求．
（2）解：△BFC是等腰三角形，理由如下： ∵ AB=AC， ∴∠ABD=∠ACB ．
∵BD平分∠ABD，CE平分∠ACB， ∴∠FBC= ∠ABC ， ∠FCB= ∠ACB， ∴ ∠FBC=∠FCB，∴BF =CF． 即△BFC是等腰三角形
【知识点】等腰三角形的判定与性质；尺规作图-作角的平分线
19．【答案】（1）证明：在△ABC与△ADC中，
，
∴△ABC≌△ADC，
∴∠B=∠D
（2）证明：∵△ABC≌△ADC，
∴∠ACB=∠ACD，
∵AE⊥BC，垂足为E，AF⊥CD，垂足为F，
∴AE=AF
【知识点】全等三角形的判定与性质；角平分线的性质
20．【答案】（1）解：如图①，在OP上任意取一点.然后以点为圆心，任意长为半半作弧.分别交OM，ON于点B，C，连接AB，AC，则.
FE与FD之间的数是关系为．
（2）解：（1）中的结论仍然成立．证明如下：如图（3），在AC上截取．连接． 平分，．
又∵，，，．．
由，
AD，CE分别是，的平分线，
可得．
．
．
由及FC为公共边，
易得，
，．
和△BCE均为等腰直角三角形，
，，
．
，
．
，
．
．
A，B，E三点在同一直线上，
．
．
（已证），
．
，
．
在△ABC和△NEC中，
【知识点】三角形全等及其性质；角平分线的性质；作图﹣轴对称；三角形全等的判定-AAS
21世纪教育网(www.21cnjy.com)
2 / 11