1.1.1正弦定理

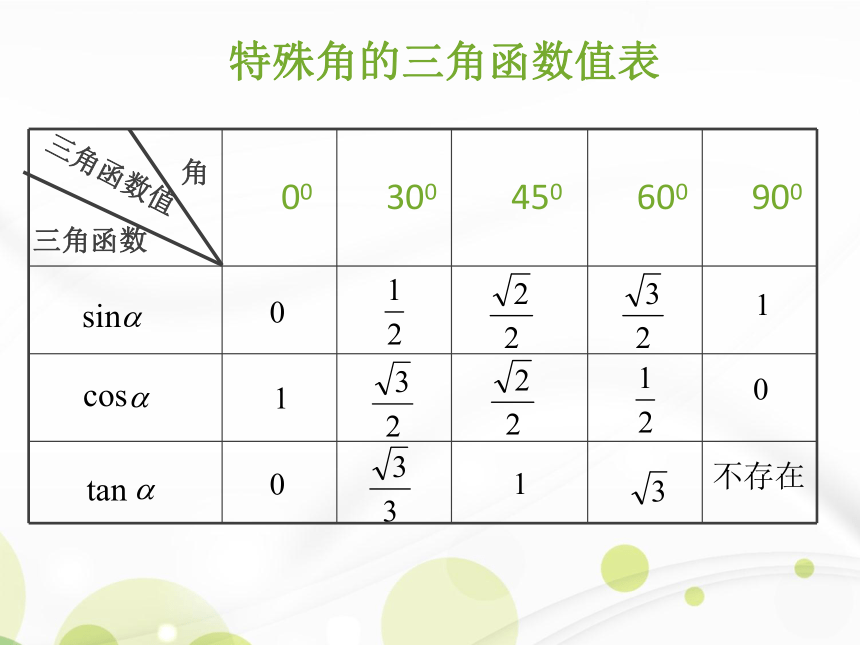
课件29张PPT。特殊角的三角函数值表三角函数三角函数值角sincostan∠A的对边∠A的邻边tanAcosA∠A的邻边斜边∠A的对边sinA斜边锐角三角函数定义回顾 复习三角形中的边角关系1、角的关系
2、边的关系
3、边角关系大角对大边（一）任意三角形中的边角关系（二）直角三角形中的边角关系 （角C为直角） 1、角的关系
2、边的关系
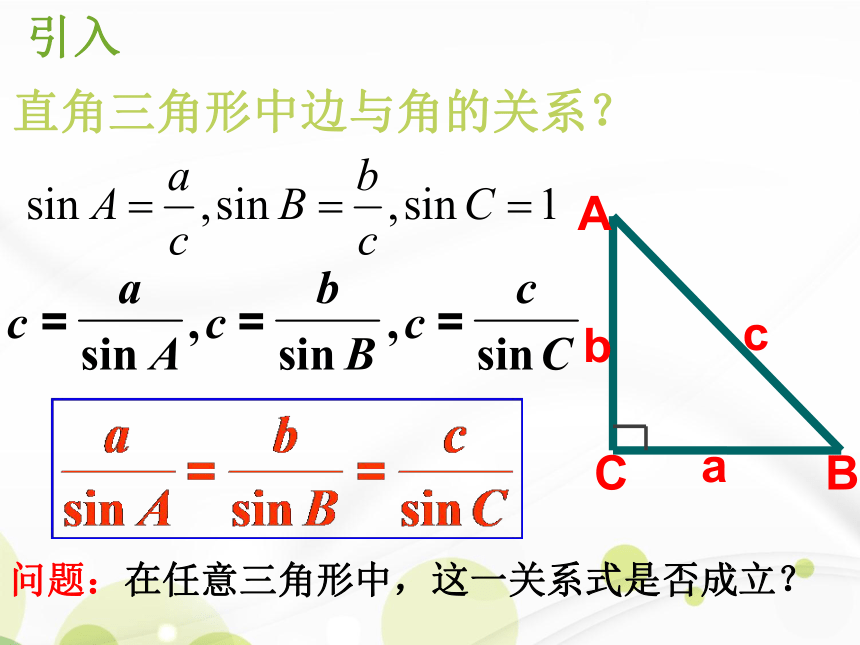
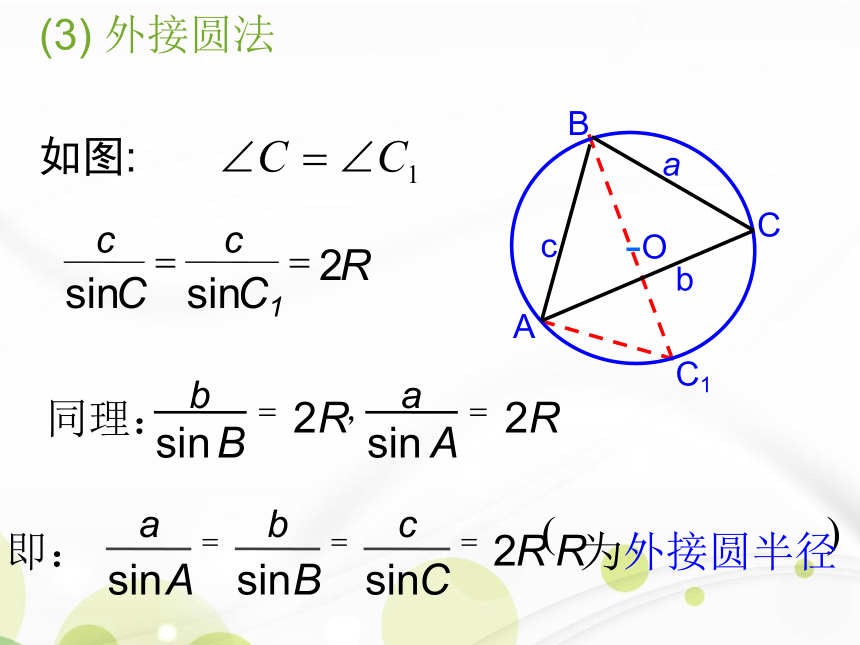
3、边角关系？1.1.1 正弦定理引入直角三角形中边与角的关系？问题：在任意三角形中，这一关系式是否成立？所以AD=csinB=bsinC, 即同理可得过点A作AD⊥BC于D,此时有　(1) 若三角形是锐角三角形, 如图学科网且可得(2) 若三角形是钝角三角形,且角C是钝角此时也有交BC延长线于D,过点A作AD⊥BC，正弦定理 在一个三角形中各边和它所对角的正弦的比相等.＝?如图:(3) 外接圆法正弦定理在一个三角形中，各边和它所对角的正弦的比相等，即 一般的，把三角形的三个角A,B,C和它们
的对边a,b,c叫做三角形的元素。已知三角形的几个元素求其他元素的过程叫做解三角形。(1) a=2RsinA, b=2RsinB, c=2RsinC；(2) sinA : sinB : sinC = a : b : c；注 意:正弦定理可以解决三角形中哪类问题：① 已知两角和一边，求其他角和边. ②
已知两边和其中一边的对角，求另一边
的对角，进而可求其他的边和角.1．在△ABC中，A＝60°，B【解析】由a＝2Rsin A，b＝2Rsin B，全优67页限时规范训练例 在△ABC 中，已知c = 10,A = 45。, C = 30。求 a , b (精确到0.01）.解： 且 ∵19.32=∵14.14=a 在 中，已知 ，求 .典型例题解：由 得 ∵ 在 中 ∴ A 为锐角 已知两边和其中一边的对角,求其他边和角时,三角形什么情况下有一解,二解,无解?课后思考已知边a,b和角Ａ，求其他边和角．Ａ为锐角Ａ为直角或钝角已知两边一对角，三角形解的个数1. 已知两角及一边解三角形一定只有一解。2. 已知两边及一边的对角解三角形，可能无解、一 解或两解。 知识归纳：2．在△ABC中，c＝10，A＝30°，则C＝(　)A．105° B．60° C．15° D．45°或135°D【解析】∴C＝45°或135°全优第4页基础夯实4．在△ABC中，a＝2，b＝2，∠A＝45°，此三角形的解的情况是(　　)A．无解 B．一解 C．两解 D．不定B【解析】∵a＝b，∴∠B＝∠A＝45°，因此该三角形只有一解．全优第4页基础夯实3．在△ABC中，若已知a＝14，B＝60°，则角C＝__________.75°【解析】由正弦定理，∴A＝45°或A＝135°(舍去)．∴C＝180°－(B＋A)＝180°－(60°＋45°)＝75°.全优67页限时规范训练3．(2013年湖南)在锐角△ABC中，角A，B所对的边长分别为a，b.则角A等于(　　)D【解析】∵在△ABC中，又△ABC为锐角三角形，全优第4页基础夯实2．(2013年陕西)设△ABC的内角A，B，C所对的边分别为a，b，c，若bcos C＋ccos B＝asin A，则△ABC的形状为(　　)A．直角三角形 B．锐角三角形
C．钝角三角形 D．不确定A【解析】因为bcos C＋ccos B＝asin A，由正弦定理，可得sin Bcos C＋sin Ccos B＝sin Asin A，所以sin(B＋C)＝sin 2A，即sin A＝sin 2A.因为A为三角形内角，所以sin A＝1，所以三角形是直角三角形．全优67页限时规范训练5．已知方程x2－(bcos A)x＋acos B＝0的两根之积等于两根之和且A，B为△ABC的内角，a，b为A，B的对边，试判断△ABC的形状．【解析】设方程的两根为x1，x2，则x1＋x2＝x1·x2，∴bcos A＝acos B.由正弦定理，得a＝2Rsin A，b＝2Rsin B，∴sin B·cos A＝sin A·cos B.∴sin(A－B)＝0，∴A＝B.∴△ABC为等腰三角形．全优67页限时规范训练【例4】 根据下列条件，判断解三角形时是否有解，若有解，有几个解．解法(1)∵A＝120°，∵A>B，∴B只有一个值．∴有一解．全优第3页典例剖析【例4】 根据下列条件，判断解三角形时是否有解，若有解，有几个解．解法全优第3页典例剖析(2)a＝60，b＝48，B＝60°；与0a，∴B>A，∴B有一锐角值和一钝角值，即有两解．