浙江省宁波市鄞州区2024-2025学年第一学期华师大艺术实验八年级期中数学试卷(含答案)
文档属性
| 名称 | 浙江省宁波市鄞州区2024-2025学年第一学期华师大艺术实验八年级期中数学试卷(含答案) | 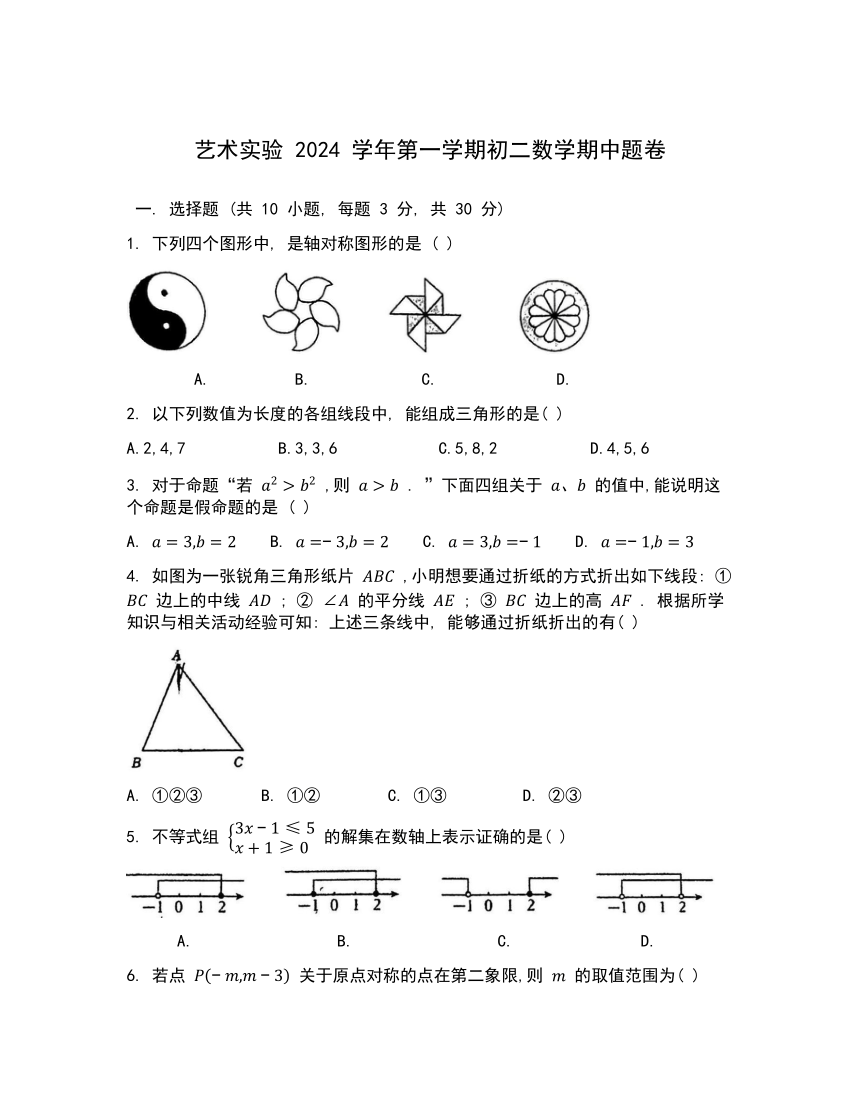 | |
| 格式 | docx | ||
| 文件大小 | 439.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-01-24 19:16:35 | ||
图片预览


文档简介
艺术实验 2024 学年第一学期初二数学期中题卷
一. 选择题 (共 10 小题, 每题 3 分, 共 30 分)
1. 下列四个图形中, 是轴对称图形的是 ( )
B. C. D.
2. 以下列数值为长度的各组线段中, 能组成三角形的是( )
A.2,4,7 B.3,3,6 C.5,8,2 D.4,5,6
3. 对于命题“若 ,则 . ”下面四组关于 的值中,能说明这个命题是假命题的是 ( )
A. B. C. D.
4. 如图为一张锐角三角形纸片 ,小明想要通过折纸的方式折出如下线段: ① 边上的中线 ; ② 的平分线 ; ③ 边上的高 . 根据所学知识与相关活动经验可知: 上述三条线中, 能够通过折纸折出的有( )
A. ①②③ B. ①② C. ①③ D. ②③
5. 不等式组 的解集在数轴上表示证确的是( )
A. B. C. D.
6. 若点 关于原点对称的点在第二象限,则 的取值范围为( )
A. B. C. D. 或
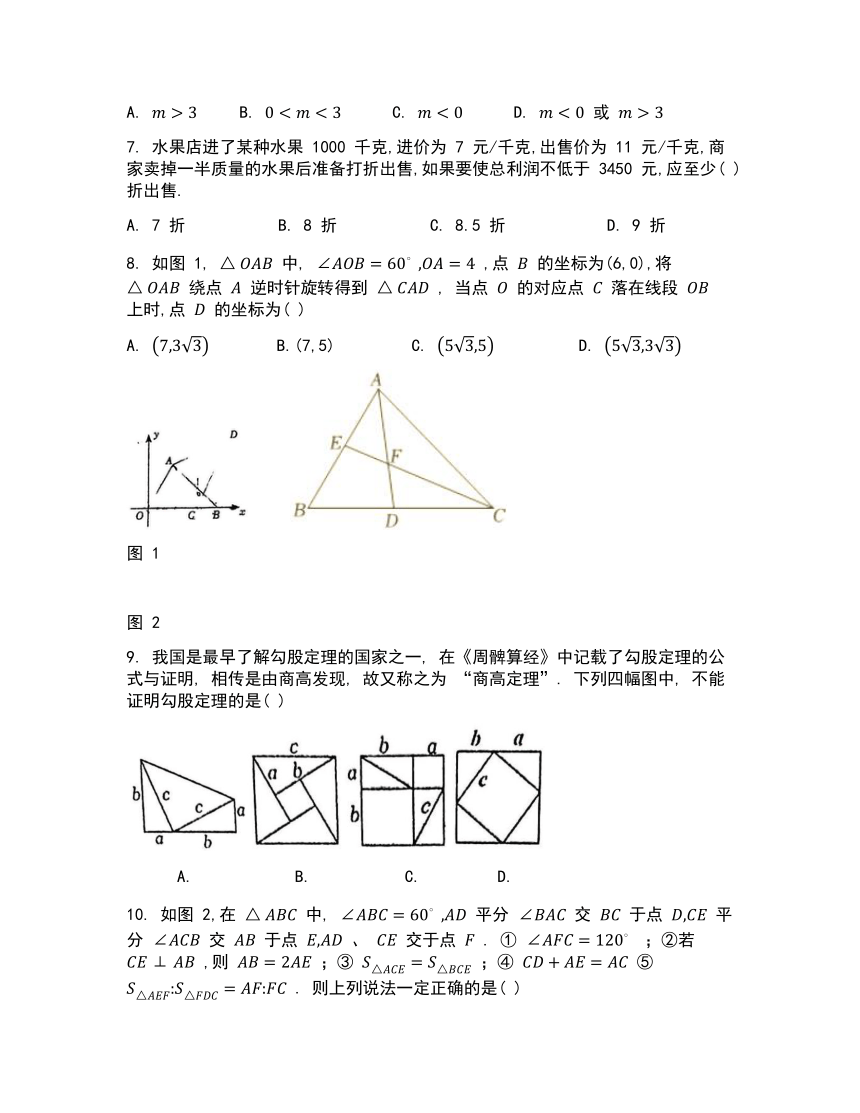
7. 水果店进了某种水果 1000 千克,进价为 7 元/千克,出售价为 11 元/千克,商家卖掉一半质量的水果后准备打折出售,如果要使总利润不低于 3450 元,应至少( )折出售.
A. 7 折 B. 8 折 C. 8.5 折 D. 9 折
8. 如图 1, 中, ,点 的坐标为(6,0),将 绕点 逆时针旋转得到 , 当点 的对应点 落在线段 上时,点 的坐标为( )
A. B.(7,5) C. D.
图 1
图 2
9. 我国是最早了解勾股定理的国家之一, 在《周髀算经》中记载了勾股定理的公式与证明, 相传是由商高发现, 故又称之为 “商高定理”. 下列四幅图中, 不能证明勾股定理的是( )
B. C. D.
10. 如图 2,在 中, 平分 交 于点 平分 交 于点 、 交于点 . ① ;②若 ,则 ;③ ;④ ⑤ . 则上列说法一定正确的是( )
A. ①②④ B. ①②④⑤ C. ①②③④ D. ①②③④⑤
二. 填空题 (共 6 小题, 每题 3 分, 共 18 分)
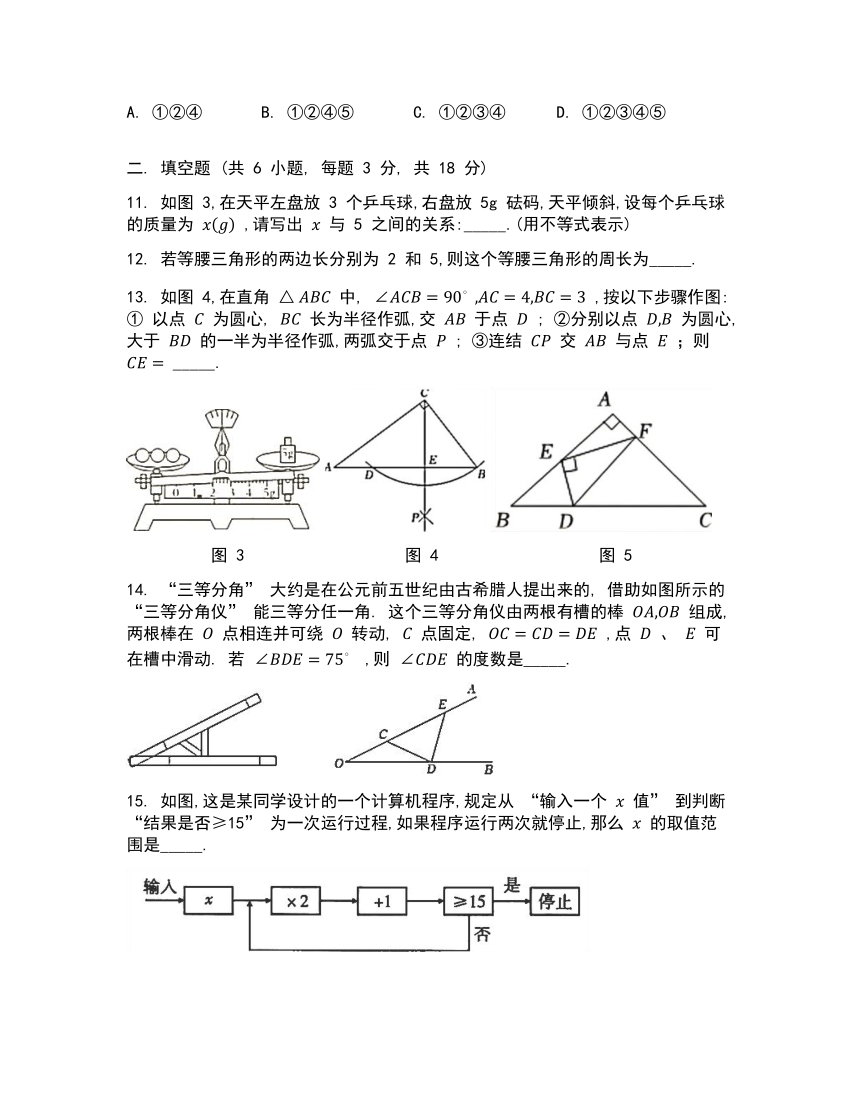
11. 如图 3,在天平左盘放 3 个乒乓球,右盘放 5g 砝码,天平倾斜,设每个乒乓球的质量为 ,请写出 与 5 之间的关系:_____.(用不等式表示)
12. 若等腰三角形的两边长分别为 2 和 5,则这个等腰三角形的周长为_____.
13. 如图 4,在直角 中, ,按以下步骤作图: ① 以点 为圆心, 长为半径作弧,交 于点 ; ②分别以点 为圆心,大于 的一半为半径作弧,两弧交于点 ; ③连结 交 与点 ;则 _____.
图 3 图 4 图 5
14. “三等分角” 大约是在公元前五世纪由古希腊人提出来的, 借助如图所示的 “三等分角仪” 能三等分任一角. 这个三等分角仪由两根有槽的棒 组成,两根棒在 点相连并可绕 转动, 点固定, ,点 、 可在槽中滑动. 若 ,则 的度数是_____.
15. 如图,这是某同学设计的一个计算机程序,规定从 “输入一个 值” 到判断 “结果是否≥15” 为一次运行过程,如果程序运行两次就停止,那么 的取值范围是_____.
16. 如图 5,在 中, ,点 E为 B的中点,点 分别为 上的点,连结 ,若 ,则 的长度为
三. 解答题 (共 8 小题, 分,共 52 分)
17. (1) 解方程组: (2)解不等式组: .
18. 已知 ,求证: .
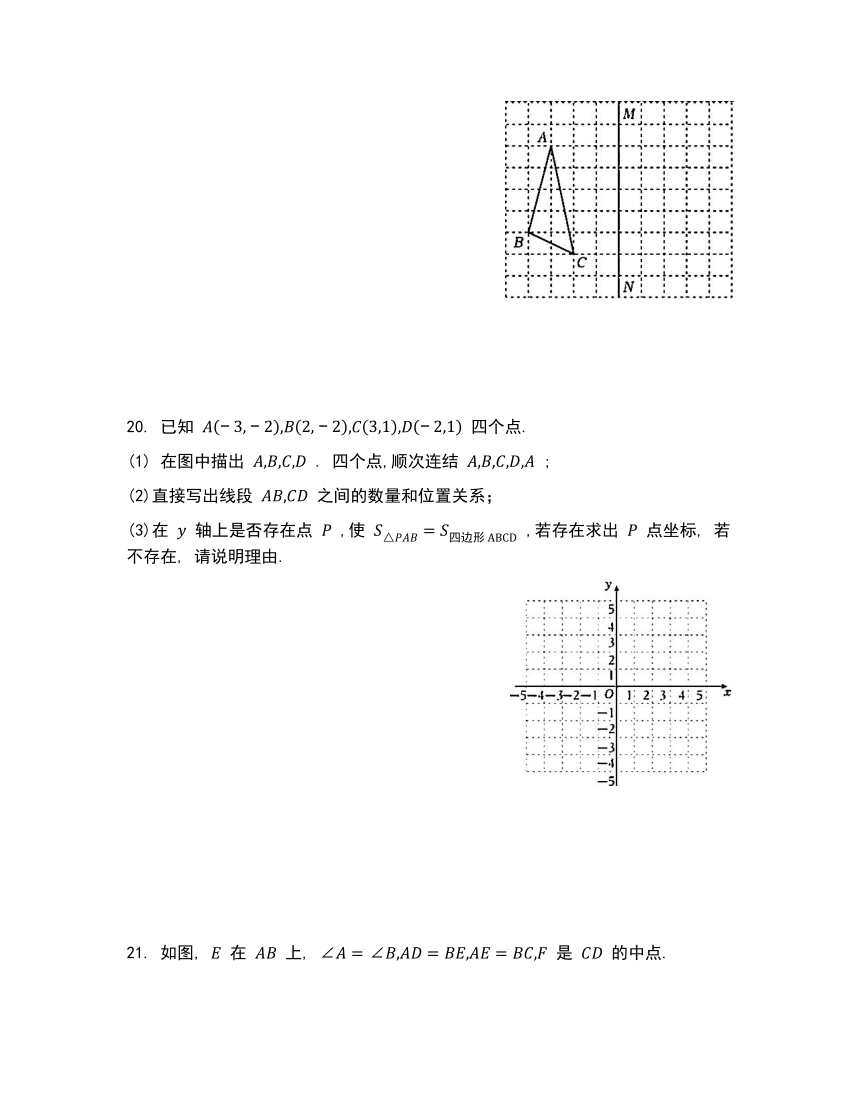
19. 如图,在正方形网格中,点 都在格点上.
( 1 )作 关于直线 对称的图形 ;
(2)若网格中最小正方形的边长为 1,则 的面积为_____;
(3)在直线 上取一点 ,求 的最小值为_____.
20. 已知 四个点.
(1) 在图中描出 . 四个点,顺次连结 ;
(2)直接写出线段 之间的数量和位置关系;
(3)在 轴上是否存在点 ,使 ,若存在求出 点坐标, 若不存在, 请说明理由.
21. 如图, 在 上, 是 的中点.
(1) 求证: ;
(2) ,求 的度数.
22. 刺绣是我国民间传统手工艺,湘绣作为中国四大刺绣之一,闻名中外,某国际旅游公司计划购买 、 两种奥运主题的湘绣作品作为纪念品. 已知购买 1 件 种湘绣作品与 2 件 种湘绣作品共需要 700 元, 购买 2 件 种湘绣作品与 3 件 种湘绣作品共需要 1200 元.
(1)求 种湘绣作品和 种湘绣作品的单价分别为多少元?
(2)该国际旅游公司计划购买 种湘绣作品和 种湘绣作品共 200 件,总费用不超过 50000 元,那么最多能购买 种湘绣作品多少件
23. 对 定义一种新运算 “ ” ,规定: . ( , 均为非零常数),等式右边的运算是通常的四则运算,例如: .
( 1 ) 已知 .
① 求 的值;
② 若关于 的不等式组 有且只有两个整数解,求字母 的取值范围;
(2)若运算 “ ” 满足加法交换律,即对于我们所学过的任意数 ,结论 “ ” 都成立,试探究 应满足的关系.
24. 已知在 中, ,点 是边 上一点, .
(1)如图 1,试说明 的理由;
(2)如图 2,过点 作 ,垂足为点 , 与 相交于点 。如果 是等腰三角形, 求 的度数.
(3)如图 3,把 以 为对称轴翻折至 ,若此时 ,求 的面积.
附加题 (4+3+3 分, 共 10 分)
1. 若直角三角形三边长为正整数, 且周长与面积数值相等, 则称此三角形为“完美直角三角形”, 求“完美直角三角形”的斜边长为_____
2. 已知 ,则 的值为_____.
3. 求 的最小值为_____.
参考答案
1-5:DDBAB 6-10:CDACB
11:3>5
12:12
13:
14:80°
15:3≤<7
16:
17解析:
(1)原方程组的解为
(2)
解不等式①得 ,
解不等式②得 ,
则不等式组的解集是 .
18解析:
证明: ,
,即 ,
在 和 ,
.
19解析:(1)如图, 即为所求.
(2) 的面积为
(3) 连接 ,交直线 于点 ,连接 ,
此时 ,为最小值.
由勾股定理得, ,
的最小值为 .
故答案为: .
20解析:
(1)画出图象如图所示:
(2)由图象可得: ;
.
设在 轴上存在点 ,使 ,
,即 ,
解得: .
在 轴上存在 , 使 .
21解析:
(1)证明: 在 和 中,
,
,
是 的中点,
.
,
,
,
,
,
,
,
的度数是 .
22解析:
(1)设 种湘绣作品的单价为 元, 种湘绣作品的单价为 元,
根据题意得: ,
解得: .
答: 种湘绣作品的单价为 300 元, 种湘绣作品的单价为 200元;
( 2 )设购买 种湘绣作品 件,则购买 种湘绣作品
(200 - m)件,
根据题意得: ,
解得: ,
的最大值为 100 .
答: 最多能购买100件 种湘绣作品.
23解析:
(1) ,
解得: ;
② , , ,
,
即 ,
解得: ,
关于 的不等式组 ,有且只有两个整数
解,
,
解得: ,
即字母 的取值范围是 ;
(2) ,
,
,
,
,
为任意数,
不一定等于 0,
,
即 所应满足的关系式是 .
24解析:
,
,
是 的一个外角,
,
,
,
.
;
(2)① ,
,
,
设 ,则 ,
,
;
② 是 的一个外角,
,
分三种情况:
当 时,
,
,
,
,
;
当 时,
,
,
,
;
当 时,
,
,
不存在 ,
综上所述:如果 是等腰三角形, 的度数为 或 . 25
附加题:
1解析:
(1)设三边长为 ,其中 是斜边,
则有
(2)代入(1)得
即
因为 所以
所以 为正整数)
所以 ,
所以 ;
,
所以,三边长为6,8,10或5,12,13. 26
2解析:
因为 ,所以 . 又因为
所以 ,即 ,所以 ,所以 .
3解析:
由题意得,代数式 的几何意义是:在x轴上找一点P,使得该点到点A(0,1)和点 B(8,-5) 的距离之和最小,作点A关于x轴的对称点A,连接AB与x轴的交点即为点P,此时 PA+PB 的值最小,且最小值为 的长,
,
,∴代数式
的最小值为 .
一. 选择题 (共 10 小题, 每题 3 分, 共 30 分)
1. 下列四个图形中, 是轴对称图形的是 ( )
B. C. D.
2. 以下列数值为长度的各组线段中, 能组成三角形的是( )
A.2,4,7 B.3,3,6 C.5,8,2 D.4,5,6
3. 对于命题“若 ,则 . ”下面四组关于 的值中,能说明这个命题是假命题的是 ( )
A. B. C. D.
4. 如图为一张锐角三角形纸片 ,小明想要通过折纸的方式折出如下线段: ① 边上的中线 ; ② 的平分线 ; ③ 边上的高 . 根据所学知识与相关活动经验可知: 上述三条线中, 能够通过折纸折出的有( )
A. ①②③ B. ①② C. ①③ D. ②③
5. 不等式组 的解集在数轴上表示证确的是( )
A. B. C. D.
6. 若点 关于原点对称的点在第二象限,则 的取值范围为( )
A. B. C. D. 或
7. 水果店进了某种水果 1000 千克,进价为 7 元/千克,出售价为 11 元/千克,商家卖掉一半质量的水果后准备打折出售,如果要使总利润不低于 3450 元,应至少( )折出售.
A. 7 折 B. 8 折 C. 8.5 折 D. 9 折
8. 如图 1, 中, ,点 的坐标为(6,0),将 绕点 逆时针旋转得到 , 当点 的对应点 落在线段 上时,点 的坐标为( )
A. B.(7,5) C. D.
图 1
图 2
9. 我国是最早了解勾股定理的国家之一, 在《周髀算经》中记载了勾股定理的公式与证明, 相传是由商高发现, 故又称之为 “商高定理”. 下列四幅图中, 不能证明勾股定理的是( )
B. C. D.
10. 如图 2,在 中, 平分 交 于点 平分 交 于点 、 交于点 . ① ;②若 ,则 ;③ ;④ ⑤ . 则上列说法一定正确的是( )
A. ①②④ B. ①②④⑤ C. ①②③④ D. ①②③④⑤
二. 填空题 (共 6 小题, 每题 3 分, 共 18 分)
11. 如图 3,在天平左盘放 3 个乒乓球,右盘放 5g 砝码,天平倾斜,设每个乒乓球的质量为 ,请写出 与 5 之间的关系:_____.(用不等式表示)
12. 若等腰三角形的两边长分别为 2 和 5,则这个等腰三角形的周长为_____.
13. 如图 4,在直角 中, ,按以下步骤作图: ① 以点 为圆心, 长为半径作弧,交 于点 ; ②分别以点 为圆心,大于 的一半为半径作弧,两弧交于点 ; ③连结 交 与点 ;则 _____.
图 3 图 4 图 5
14. “三等分角” 大约是在公元前五世纪由古希腊人提出来的, 借助如图所示的 “三等分角仪” 能三等分任一角. 这个三等分角仪由两根有槽的棒 组成,两根棒在 点相连并可绕 转动, 点固定, ,点 、 可在槽中滑动. 若 ,则 的度数是_____.
15. 如图,这是某同学设计的一个计算机程序,规定从 “输入一个 值” 到判断 “结果是否≥15” 为一次运行过程,如果程序运行两次就停止,那么 的取值范围是_____.
16. 如图 5,在 中, ,点 E为 B的中点,点 分别为 上的点,连结 ,若 ,则 的长度为
三. 解答题 (共 8 小题, 分,共 52 分)
17. (1) 解方程组: (2)解不等式组: .
18. 已知 ,求证: .
19. 如图,在正方形网格中,点 都在格点上.
( 1 )作 关于直线 对称的图形 ;
(2)若网格中最小正方形的边长为 1,则 的面积为_____;
(3)在直线 上取一点 ,求 的最小值为_____.
20. 已知 四个点.
(1) 在图中描出 . 四个点,顺次连结 ;
(2)直接写出线段 之间的数量和位置关系;
(3)在 轴上是否存在点 ,使 ,若存在求出 点坐标, 若不存在, 请说明理由.
21. 如图, 在 上, 是 的中点.
(1) 求证: ;
(2) ,求 的度数.
22. 刺绣是我国民间传统手工艺,湘绣作为中国四大刺绣之一,闻名中外,某国际旅游公司计划购买 、 两种奥运主题的湘绣作品作为纪念品. 已知购买 1 件 种湘绣作品与 2 件 种湘绣作品共需要 700 元, 购买 2 件 种湘绣作品与 3 件 种湘绣作品共需要 1200 元.
(1)求 种湘绣作品和 种湘绣作品的单价分别为多少元?
(2)该国际旅游公司计划购买 种湘绣作品和 种湘绣作品共 200 件,总费用不超过 50000 元,那么最多能购买 种湘绣作品多少件
23. 对 定义一种新运算 “ ” ,规定: . ( , 均为非零常数),等式右边的运算是通常的四则运算,例如: .
( 1 ) 已知 .
① 求 的值;
② 若关于 的不等式组 有且只有两个整数解,求字母 的取值范围;
(2)若运算 “ ” 满足加法交换律,即对于我们所学过的任意数 ,结论 “ ” 都成立,试探究 应满足的关系.
24. 已知在 中, ,点 是边 上一点, .
(1)如图 1,试说明 的理由;
(2)如图 2,过点 作 ,垂足为点 , 与 相交于点 。如果 是等腰三角形, 求 的度数.
(3)如图 3,把 以 为对称轴翻折至 ,若此时 ,求 的面积.
附加题 (4+3+3 分, 共 10 分)
1. 若直角三角形三边长为正整数, 且周长与面积数值相等, 则称此三角形为“完美直角三角形”, 求“完美直角三角形”的斜边长为_____
2. 已知 ,则 的值为_____.
3. 求 的最小值为_____.
参考答案
1-5:DDBAB 6-10:CDACB
11:3>5
12:12
13:
14:80°
15:3≤<7
16:
17解析:
(1)原方程组的解为
(2)
解不等式①得 ,
解不等式②得 ,
则不等式组的解集是 .
18解析:
证明: ,
,即 ,
在 和 ,
.
19解析:(1)如图, 即为所求.
(2) 的面积为
(3) 连接 ,交直线 于点 ,连接 ,
此时 ,为最小值.
由勾股定理得, ,
的最小值为 .
故答案为: .
20解析:
(1)画出图象如图所示:
(2)由图象可得: ;
.
设在 轴上存在点 ,使 ,
,即 ,
解得: .
在 轴上存在 , 使 .
21解析:
(1)证明: 在 和 中,
,
,
是 的中点,
.
,
,
,
,
,
,
,
的度数是 .
22解析:
(1)设 种湘绣作品的单价为 元, 种湘绣作品的单价为 元,
根据题意得: ,
解得: .
答: 种湘绣作品的单价为 300 元, 种湘绣作品的单价为 200元;
( 2 )设购买 种湘绣作品 件,则购买 种湘绣作品
(200 - m)件,
根据题意得: ,
解得: ,
的最大值为 100 .
答: 最多能购买100件 种湘绣作品.
23解析:
(1) ,
解得: ;
② , , ,
,
即 ,
解得: ,
关于 的不等式组 ,有且只有两个整数
解,
,
解得: ,
即字母 的取值范围是 ;
(2) ,
,
,
,
,
为任意数,
不一定等于 0,
,
即 所应满足的关系式是 .
24解析:
,
,
是 的一个外角,
,
,
,
.
;
(2)① ,
,
,
设 ,则 ,
,
;
② 是 的一个外角,
,
分三种情况:
当 时,
,
,
,
,
;
当 时,
,
,
,
;
当 时,
,
,
不存在 ,
综上所述:如果 是等腰三角形, 的度数为 或 . 25
附加题:
1解析:
(1)设三边长为 ,其中 是斜边,
则有
(2)代入(1)得
即
因为 所以
所以 为正整数)
所以 ,
所以 ;
,
所以,三边长为6,8,10或5,12,13. 26
2解析:
因为 ,所以 . 又因为
所以 ,即 ,所以 ,所以 .
3解析:
由题意得,代数式 的几何意义是:在x轴上找一点P,使得该点到点A(0,1)和点 B(8,-5) 的距离之和最小,作点A关于x轴的对称点A,连接AB与x轴的交点即为点P,此时 PA+PB 的值最小,且最小值为 的长,
,
,∴代数式
的最小值为 .
同课章节目录
