上海市浦东新区建平中学西校2024-2025学年八年级(上)期末数学试卷(含答案)
文档属性
| 名称 | 上海市浦东新区建平中学西校2024-2025学年八年级(上)期末数学试卷(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 73.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-01-24 19:20:20 | ||
图片预览



文档简介
上海市浦东新区建平中学西校2024-2025学年八年级(上)期末数学试卷
一、选择题:本题共6小题,每小题3分,共18分。在每小题给出的选项中,只有一项是符合题目要求的。
1.下列二次根式中,最简二次根式是( )
A. B. C. D.
2.下列计算正确的是( )
A. B.
C. D.
3.下列关于的方程中,一定有实数根的是( )
A. B.
C. D.
4.已知函数中随的增大而增大,那么它和函数在同一直角坐标平面内的大致图象可能是( )
A. B. C. D.
5.已知、、分别是的三边,根据下列条件能判定为直角三角形的是( )
A. ,, B. ,,
C. ,, D. ,,
6.下列命题中,假命题是( )
A. 三角形三条边的垂直平分线的交点到三角形三个顶点的距离相等
B. 三角形三个内角的平分线的交点到三角形三条边的距离相等
C. 两腰对应相等的两个等腰三角形全等
D. 一条直角边和另一条直角边上的中线对应相等的两个直角三角形全等
二、填空题:本题共12小题,每小题3分,共36分。
7.函数的定义域为______.
8.已知,那么 ______.
9.的有理化因式是______.
10.方程的解是______.
11.写出“全等三角形的面积相等”的逆命题_____________________.
12.如果反比例函数的图象在的范围内,随的增大而增大,那么的取值范围是______.
13.某工厂七月份的产值是万元,计划九月份的产值要达到万元,如果每月产值的增长率相同,则这个增长率是______.
14.在实数范围内分解因式:______.
15.如图,垂直平分,垂直平分,若,则______度.
16.以线段为底边的等腰三角形的顶点的轨迹是______.
17.我们把两个不全等但面积相等的三角形叫做一对偏等积三角形已知与是一对面积都等于的偏等积三角形,且,,那么的长等于______结果用含和的代数式表示.
18.已知和是矩形的两条对角线,将沿直线翻折后,点落在点处,与矩形的重叠部分是,如果,,那么长为______.
三、计算题:本大题共2小题,共12分。
19.计算:.
20.用配方法解方程:.
四、解答题:本题共6小题,共48分。解答应写出文字说明,证明过程或演算步骤。
21.本小题分
已知关于的方程.
此方程有一个根为时,求的值和此方程的另一个根;
此方程有两个不相等的实数根时,求的取值范围.
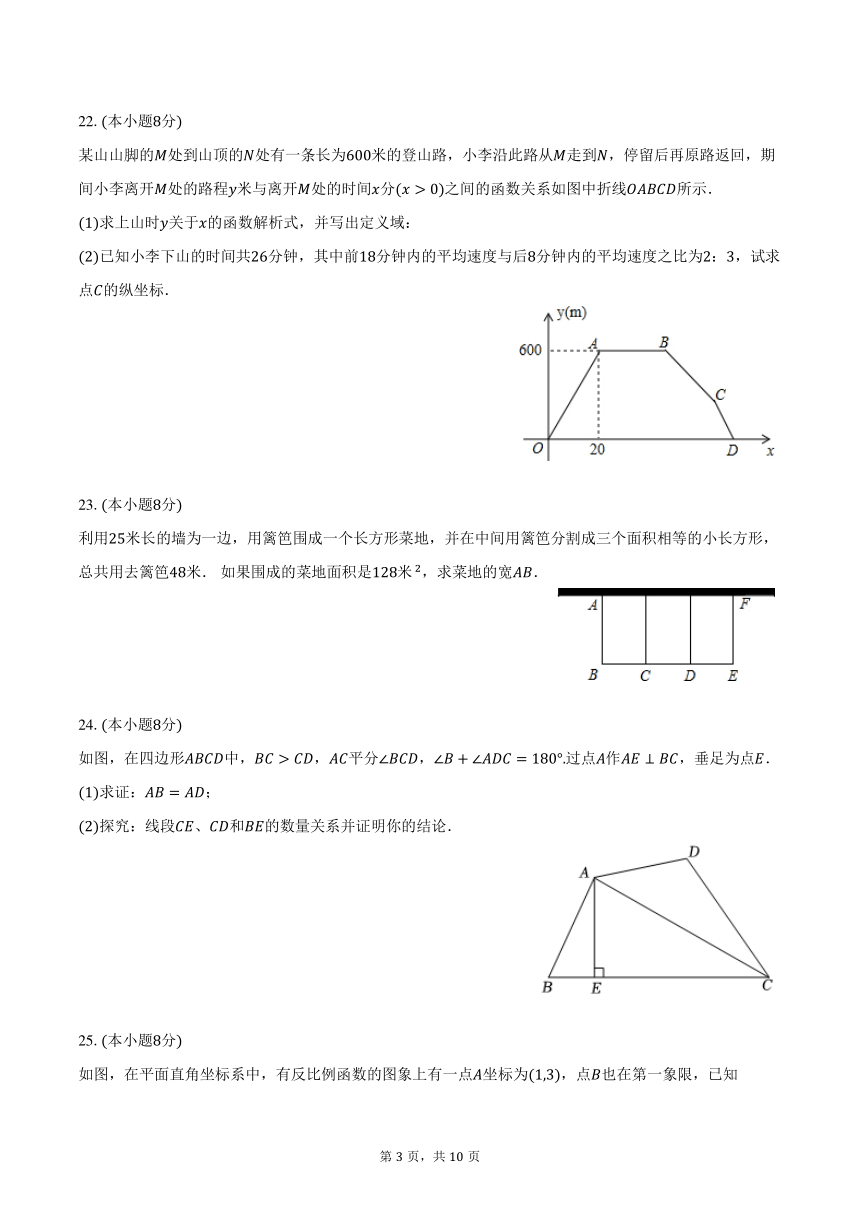
22.本小题分
某山山脚的处到山顶的处有一条长为米的登山路,小李沿此路从走到,停留后再原路返回,期间小李离开处的路程米与离开处的时间分之间的函数关系如图中折线所示.
求上山时关于的函数解析式,并写出定义域:
已知小李下山的时间共分钟,其中前分钟内的平均速度与后分钟内的平均速度之比为:,试求点的纵坐标.
23.本小题分
利用米长的墙为一边,用篱笆围成一个长方形菜地,并在中间用篱笆分割成三个面积相等的小长方形,总共用去篱笆米. 如果围成的菜地面积是米,求菜地的宽.
24.本小题分
如图,在四边形中,,平分,过点作,垂足为点.
求证:;
探究:线段、和的数量关系并证明你的结论.
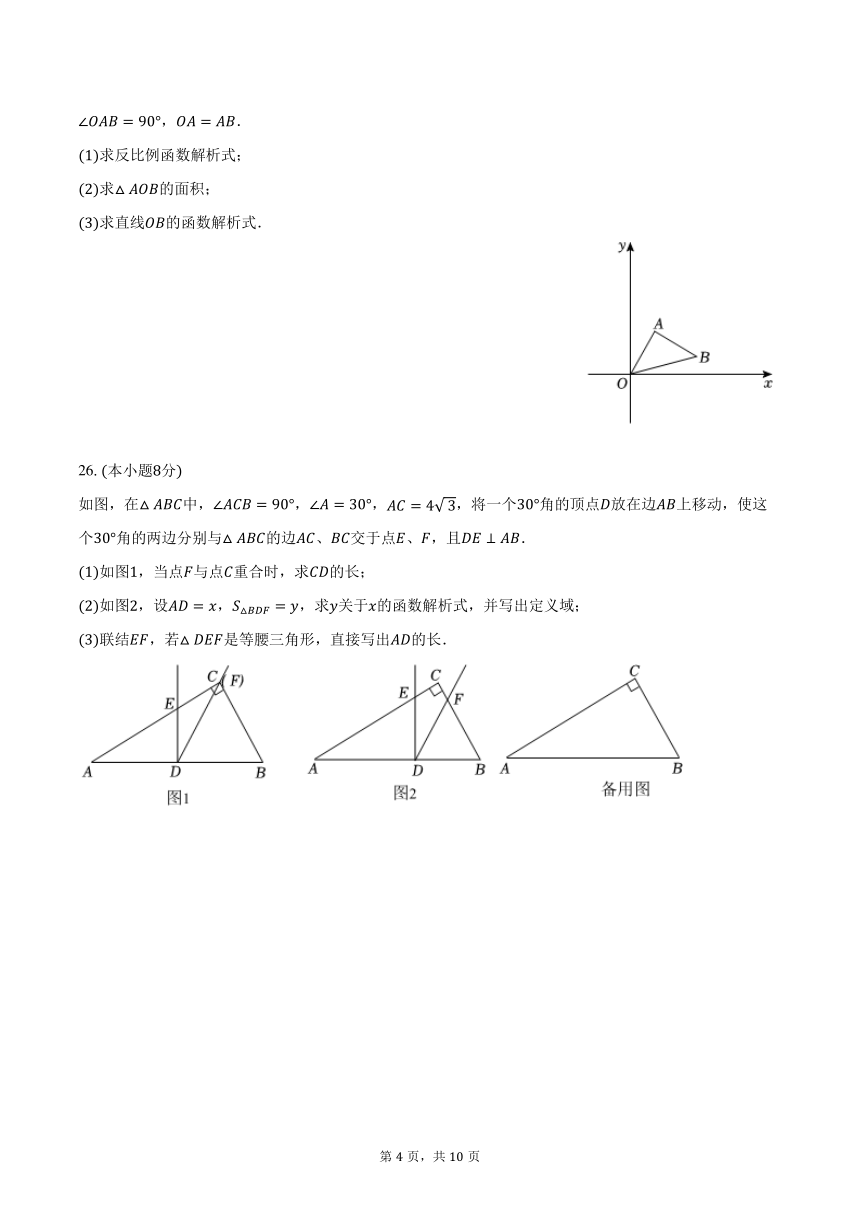
25.本小题分
如图,在平面直角坐标系中,有反比例函数的图象上有一点坐标为,点也在第一象限,已知,.
求反比例函数解析式;
求的面积;
求直线的函数解析式.
26.本小题分
如图,在中,,,,将一个角的顶点放在边上移动,使这个角的两边分别与的边、交于点、,且.
如图,当点与点重合时,求的长;
如图,设,,求关于的函数解析式,并写出定义域;
联结,若是等腰三角形,直接写出的长.
1.【答案】
2.【答案】
3.【答案】
4.【答案】
5.【答案】
6.【答案】
7.【答案】
8.【答案】
9.【答案】
10.【答案】,
11.【答案】面积相等的三角形全等
12.【答案】
13.【答案】
14.【答案】
15.【答案】
16.【答案】线段的垂直平分线与的交点除外
17.【答案】
18.【答案】或
19.【答案】解:原式
.
20.【答案】解:,
,即,
或,
,.
21.【答案】解:设方程的另一个根为,
根据根与系数的关系得,,
,
解得,
即方程的另一个根为,
,
;
根据题意得且,
解得且,
即的取值范围为且.
22.【答案】解:设上山时关于的函数解析式为,
根据已知可得:,
解得:.
故上山时关于的函数解析式为.
设下山前分钟内的平均速度为,后分钟内的平均速度为,
由已知得:,
解得:.
故米.
答:点的纵坐标为.
23.【答案】解:设菜地的宽为米,则长度为米
由题意得
解得,
当时,不符题意舍去;
当时,符合题意.
答:菜地的宽度为米.
24.【答案】证明:在上截取,连接,
于点,
垂直平分,
,
,
,,
,
平分,
,
在和中,
,
≌,
,
.
解:,
证明:由得,≌,
,
,且,
.
25.【答案】解:设反比例函数的表达式为:,
将点的坐标代入上式得:,
则函数的表达式为:;
由题意得,为等腰直角三角形,
则的面积;
过点作轴于点,交过点和轴的平行线于点,
,,
,
,,
则≌,
则,,
则点,
设直线的表达式为:,
则,则,
故直线的表达式为:
26.【答案】解:,
,
,,
,
,
,
,
,
,
,
,
,,
,
;
过作于点,
点在边上移动,
,
,,
,
,
为等边三角形,
,
,,
,
,
在中,,
,定义域为;
当时,如图,
,,,
,
,
,
,
解得:,即;
当时,如图,
,
,
,
解得:,即;
综上所述:或.
第1页,共1页
一、选择题:本题共6小题,每小题3分,共18分。在每小题给出的选项中,只有一项是符合题目要求的。
1.下列二次根式中,最简二次根式是( )
A. B. C. D.
2.下列计算正确的是( )
A. B.
C. D.
3.下列关于的方程中,一定有实数根的是( )
A. B.
C. D.
4.已知函数中随的增大而增大,那么它和函数在同一直角坐标平面内的大致图象可能是( )
A. B. C. D.
5.已知、、分别是的三边,根据下列条件能判定为直角三角形的是( )
A. ,, B. ,,
C. ,, D. ,,
6.下列命题中,假命题是( )
A. 三角形三条边的垂直平分线的交点到三角形三个顶点的距离相等
B. 三角形三个内角的平分线的交点到三角形三条边的距离相等
C. 两腰对应相等的两个等腰三角形全等
D. 一条直角边和另一条直角边上的中线对应相等的两个直角三角形全等
二、填空题:本题共12小题,每小题3分,共36分。
7.函数的定义域为______.
8.已知,那么 ______.
9.的有理化因式是______.
10.方程的解是______.
11.写出“全等三角形的面积相等”的逆命题_____________________.
12.如果反比例函数的图象在的范围内,随的增大而增大,那么的取值范围是______.
13.某工厂七月份的产值是万元,计划九月份的产值要达到万元,如果每月产值的增长率相同,则这个增长率是______.
14.在实数范围内分解因式:______.
15.如图,垂直平分,垂直平分,若,则______度.
16.以线段为底边的等腰三角形的顶点的轨迹是______.
17.我们把两个不全等但面积相等的三角形叫做一对偏等积三角形已知与是一对面积都等于的偏等积三角形,且,,那么的长等于______结果用含和的代数式表示.
18.已知和是矩形的两条对角线,将沿直线翻折后,点落在点处,与矩形的重叠部分是,如果,,那么长为______.
三、计算题:本大题共2小题,共12分。
19.计算:.
20.用配方法解方程:.
四、解答题:本题共6小题,共48分。解答应写出文字说明,证明过程或演算步骤。
21.本小题分
已知关于的方程.
此方程有一个根为时,求的值和此方程的另一个根;
此方程有两个不相等的实数根时,求的取值范围.
22.本小题分
某山山脚的处到山顶的处有一条长为米的登山路,小李沿此路从走到,停留后再原路返回,期间小李离开处的路程米与离开处的时间分之间的函数关系如图中折线所示.
求上山时关于的函数解析式,并写出定义域:
已知小李下山的时间共分钟,其中前分钟内的平均速度与后分钟内的平均速度之比为:,试求点的纵坐标.
23.本小题分
利用米长的墙为一边,用篱笆围成一个长方形菜地,并在中间用篱笆分割成三个面积相等的小长方形,总共用去篱笆米. 如果围成的菜地面积是米,求菜地的宽.
24.本小题分
如图,在四边形中,,平分,过点作,垂足为点.
求证:;
探究:线段、和的数量关系并证明你的结论.
25.本小题分
如图,在平面直角坐标系中,有反比例函数的图象上有一点坐标为,点也在第一象限,已知,.
求反比例函数解析式;
求的面积;
求直线的函数解析式.
26.本小题分
如图,在中,,,,将一个角的顶点放在边上移动,使这个角的两边分别与的边、交于点、,且.
如图,当点与点重合时,求的长;
如图,设,,求关于的函数解析式,并写出定义域;
联结,若是等腰三角形,直接写出的长.
1.【答案】
2.【答案】
3.【答案】
4.【答案】
5.【答案】
6.【答案】
7.【答案】
8.【答案】
9.【答案】
10.【答案】,
11.【答案】面积相等的三角形全等
12.【答案】
13.【答案】
14.【答案】
15.【答案】
16.【答案】线段的垂直平分线与的交点除外
17.【答案】
18.【答案】或
19.【答案】解:原式
.
20.【答案】解:,
,即,
或,
,.
21.【答案】解:设方程的另一个根为,
根据根与系数的关系得,,
,
解得,
即方程的另一个根为,
,
;
根据题意得且,
解得且,
即的取值范围为且.
22.【答案】解:设上山时关于的函数解析式为,
根据已知可得:,
解得:.
故上山时关于的函数解析式为.
设下山前分钟内的平均速度为,后分钟内的平均速度为,
由已知得:,
解得:.
故米.
答:点的纵坐标为.
23.【答案】解:设菜地的宽为米,则长度为米
由题意得
解得,
当时,不符题意舍去;
当时,符合题意.
答:菜地的宽度为米.
24.【答案】证明:在上截取,连接,
于点,
垂直平分,
,
,
,,
,
平分,
,
在和中,
,
≌,
,
.
解:,
证明:由得,≌,
,
,且,
.
25.【答案】解:设反比例函数的表达式为:,
将点的坐标代入上式得:,
则函数的表达式为:;
由题意得,为等腰直角三角形,
则的面积;
过点作轴于点,交过点和轴的平行线于点,
,,
,
,,
则≌,
则,,
则点,
设直线的表达式为:,
则,则,
故直线的表达式为:
26.【答案】解:,
,
,,
,
,
,
,
,
,
,
,
,,
,
;
过作于点,
点在边上移动,
,
,,
,
,
为等边三角形,
,
,,
,
,
在中,,
,定义域为;
当时,如图,
,,,
,
,
,
,
解得:,即;
当时,如图,
,
,
,
解得:,即;
综上所述:或.
第1页,共1页
同课章节目录
