四川省成都市锦江区2024-2025学年九年级(上)期末数学试卷(一诊)(含答案)
文档属性
| 名称 | 四川省成都市锦江区2024-2025学年九年级(上)期末数学试卷(一诊)(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 135.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-01-24 19:27:57 | ||
图片预览




文档简介
四川省成都市锦江区2024-2025学年九年级(上)期末数学试卷(一诊)
一、选择题:本题共8小题,每小题4分,共32分。在每小题给出的选项中,只有一项是符合题目要求的。
1.如图所示的几何体,其主视图是( )
A.
B.
C.
D.
2.若是一元二次方程的一个根,则的值为( )
A. B. C. D.
3.如图,直线,若,,,则的长为( )
A.
B.
C.
D.
4.如图,菱形的边长,对角线,则菱形的面积为( )
A.
B.
C.
D.
5.一个口袋中有红球、白球共个,这些球除颜色外都相同,将口袋中的球搅拌均匀,从中随机摸出一个球,记下它的颜色后再放回口袋中不断重复这一过程,共摸了次球,发现有次摸到红球,请估计这个口袋中红球的数量最有可能是( )
A. B. C. D.
6.如图,公园原有一块正方形空地,后来从这块空地上划出部分区域栽种鲜花,原空地一边减少了,另一边减少了,剩余空地面积为,设原正方形空地的边长是,根据题意,可列方程为( )
A.
B.
C.
D.
7.已知点,在反比例函数的图象上,则下列说法正确的是( )
A. 当时, B. 当时,
C. 当时, D. 当时,
8.如图,在平面直角坐标系中,的三个顶点,,的坐标分别为,,以原点为位似中心,作的位似图形,且与的相似比为:,点,,的对应点分别为,,,则点的坐标是( )
A. B.
C. 或 D. 或
二、填空题:本题共10小题,每小题4分,共40分。
9.若,则______.
10.已知关于的一元二次方程有两个相等的实数根,则 ______.
11.已知反比例函数的图象经过,两点,若点的坐标为,则点的坐标可能是______写一个即可.
12.如图,在正方形的对角线上取点使,连接,过点作交于点,则的大小为______.
13.如图,在中,,,,以点为圆心,长为半径画弧,交于点,再分别以,为圆心,大于长为半径画弧,两弧交于点,,作直线交于点,交于点,则的长为______.
14.若,是一元二次方程的两个实数根,则的值为______.
15.如图,在菱形中,,连接,点是线段上一点,过点作,,垂足分别为点,若,则的值为______.
16.如图,在平面直角坐标系中,直线与反比例函数的图象交于点,点在轴的负半轴上,连接若,的面积为,则的值为______.
17.如图所示两个矩形和,若矩形的周长是矩形的周长的倍,矩形的面积也是矩形的面积的倍,则称为矩形相对于矩形的“共比系数”若时,矩形相对于矩形的“共比系数”为,则 ______;若,均为正整数,则矩形相对于矩形的“共比系数”为的概率为______.
18.如图,在四边形中,,,对角线平分过点作于点,平分交于点,交于点若,,则的长为______.
三、解答题:本题共8小题,共78分。解答应写出文字说明,证明过程或演算步骤。
19.本小题分
计算:;
解方程:.
20.本小题分
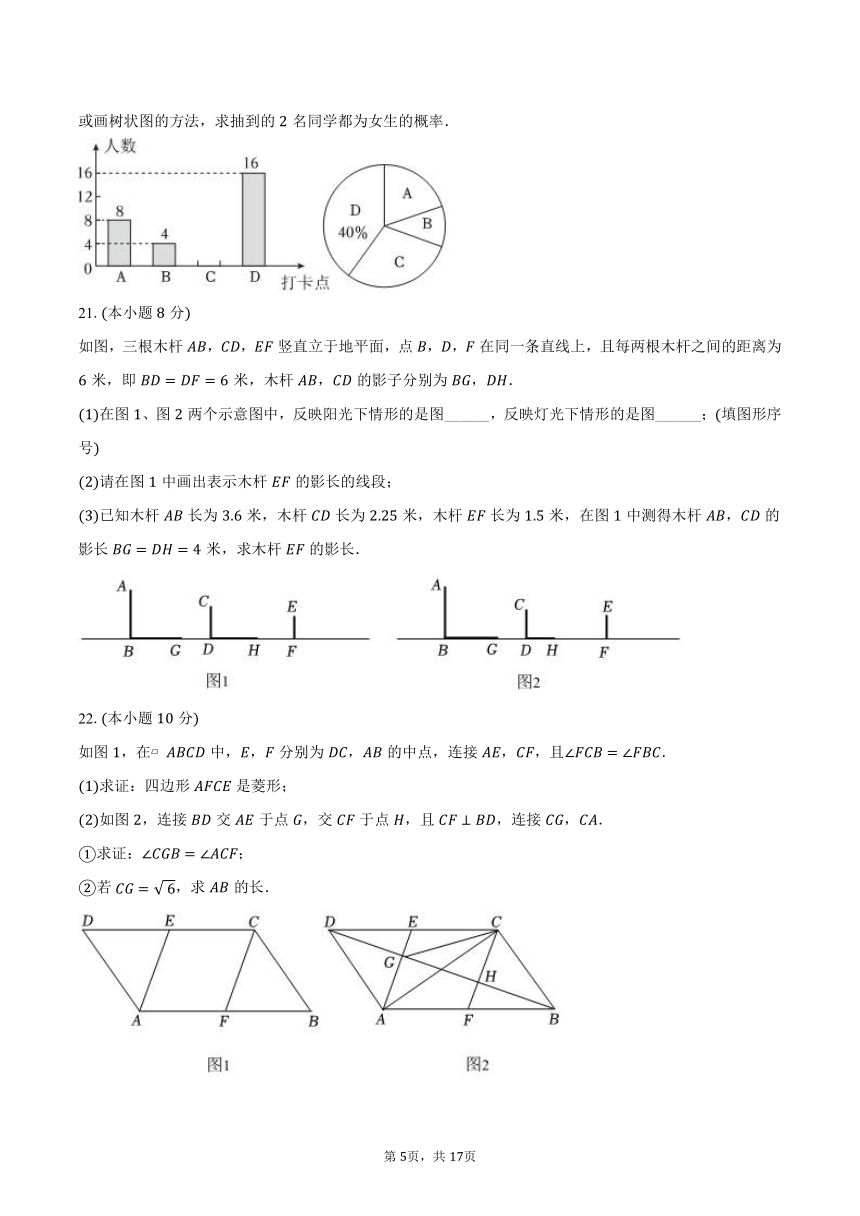
随着气温日渐走低,成都的银杏也渐渐褪去青绿,悄然变黄为鼓励同学们利用课余时间走进成都街头巷尾,发现银杏之美丽,感受自然之神奇,某校随机对该校部分学生进行了“你心中的最美银杏打卡点”问卷调查问卷设置了四个选项:文殊院;青羊宫;百花潭公园;电子科技大学通过调查得到下列不完整的统计图请结合统计图,回答下列问题:
求本次调查中接受调查的学生人数;
补全条形统计图;
在选择的四名学生中,有名男生,名女生现随机抽取其中名同学担任“银杏使者”,请用列表或画树状图的方法,求抽到的名同学都为女生的概率.
21.本小题分
如图,三根木杆,,竖直立于地平面,点,,在同一条直线上,且每两根木杆之间的距离为米,即米,木杆,的影子分别为,.
在图、图两个示意图中,反映阳光下情形的是图______,反映灯光下情形的是图______;填图形序号
请在图中画出表示木杆的影长的线段;
已知木杆长为米,木杆长为米,木杆长为米,在图中测得木杆,的影长米,求木杆的影长.
22.本小题分
如图,在 中,,分别为,的中点,连接,,且.
求证:四边形是菱形;
如图,连接交于点,交于点,且,连接,.
求证:;
若,求的长.
23.本小题分
如图,在平面直角坐标系中,点坐标为,点坐标为,平移线段得线段,连接,反比例函数的图象经过点,交直线于,两点.
若,,求反比例函数的表达式;
试探究的值是否为定值,若是,请求出;若不是,请说明理由;
如图,取线段的中点,连接,若,求所在直线的表达式.
24.本小题分
“骑行安全最重要,安全头盔要戴好”年月日起,新修订的成都市非机动车管理条例正式实施,对驾驶非机动车闯红灯、不戴头盔、逆行等违法行为做出了规范据了解,某经销商以元个的价格购入一批头盔,按元个的价格销售一段时间后,连续两次对该头盔进行降价,两次降价后,该头盔的售价为元个若该经销商两次降价的百分率相同,求每次降价的百分率;
市场调研表明:当头盔售价为元个时,每月能够售出个,当售价每降元时,则月销量能增加个若要使月销售利润为元,则头盔的售价应为多少元?
25.本小题分
如图,在平面直角坐标系中,反比例函数图象上有,两点,其中点在点右侧,连接,,.
如图,设点坐标为,若,,且.
求的值;
若的面积为,求点的坐标;
如图,延长交反比例函数的图象于点,连接,点为上一点,连接并延长交于点若的面积与的面积相等,是否存在直线,使得点始终在该直线下方,若存在,请求出的最小值;若不存在,请说明理由.
26.本小题分
如图,在中,为边上一点,交于,延长,相交于点,.
求证:;
连接,若是以为腰的等腰三角形,,求的值;
如图,在中,,,,为直线下方一点,点关于直线的对称点恰好在的延长线上,连接,,若,求的长.
1.【答案】
2.【答案】
3.【答案】
4.【答案】
5.【答案】
6.【答案】
7.【答案】
8.【答案】
9.【答案】
10.【答案】
11.【答案】答案不唯一
12.【答案】
13.【答案】
14.【答案】
15.【答案】
16.【答案】
17.【答案】或
18.【答案】
19.【答案】解:原式
提取公因式得,
或,
,.
20.【答案】解:本次调查中接受调查的学生人数为人.
选择的人数为人.
补全条形统计图如图所示.
列表如下:
男 女 女 女
男 男,女 男,女 男,女
女 女,男 女,女 女,女
女 女,男 女,女 女,女
女 女,男 女,女 女,女
共有种等可能的结果,其中抽到的名同学都为女生的结果有种,
抽到的名同学都为女生的概率为.
21.【答案】
22.【答案】证明:四边形是平行四边形,
,,
,分别为,的中点,
,,
,
四边形是平行四边形,
,
,
,
四边形是菱形;
证明:,
,
四边形是菱形,
,,
,
,
,
,
,
;
解:,
∽,
,
,
,
设,,
,
,
,
,,
,
,
,
,
舍去负值,
.
23.【答案】解:当,时,,.
根据线段平移的性质,.
点坐标为.
由反比例函数表达式得.
反比例函数的表达式为.
如图,过点作轴的垂线交轴于点.
轴.
由平行线分线段成比例得:.
,,,.
.
点在反比例函数的图象上,同理可得点的坐标为.
.
.
.
.
,.
四边形是平行四边形.
.
.
故的值为定值.
设直线的函数表达式为,把、两点坐标代入得:
,解得.
直线的表达式为.
由于反比例函数表达式为,与直线函数表达式联立得:
.
整理得.
.
,.
点的坐标为也是线段的中点.
根据线段平移的性质可得点坐标为,则.
同理,由两点坐标根据待定系数法求得的解析式为:.
过点作轴,垂足为,过点作与延长线交于点,再过点作轴,垂足为.
,
.
在和中,,
.
∽.
.
,
点在直线上,
,
代入和得:,
整理得:.
又,则,代入上式得.
.
直线的解析式为.
24.【答案】解:设每次降价的百分率为,
根据题意得:,
解得或舍去,
每次降价的百分率为;
设头盔的售价应为元,
根据题意得:,
整理得,
解得或,
头盔的售价应为元或元.
25.【答案】解:,且,
,,
点坐标为,
;
过点作轴于点,过点作轴于点,
设点的坐标为,
,
,
,即,
整理可得:,
解得负值舍去,
点的坐标为;
连接,
,
,
,
,
为中点,
为中点,
,
点坐标为,
点坐标为,
反比例函数表达式为,
设点的坐标为,
点的坐标为,
点的坐标为,
,
,
点始终在直线的下方,
的最小值为.
26.【答案】证明:,
,
又,
,
∽,
,
,
,
;
解:,
设,,
在中,由勾股定理可得,
当时,
,
,
,
,
,
在和中,
,,
∽,
,
,
;
当时,
同理可得,
,
,
,
∽,
;
综上所述,的值为或;
如图,点关于直线的对称点恰好在的延长线上,
连接,延长交于点,过点作交延长线于点,连接,
点关于直线的对称点恰好在的延长线上,
,,
,
∽,
,
,,
,
设,,
,,
在和中,
,,
∽,
,
,
,
,
,
设,,则,,
,
在中,由勾股定理可得:,
整理可得:,
解得负值舍去,
,
在中,由勾股定理可得,
即.
第1页,共1页
一、选择题:本题共8小题,每小题4分,共32分。在每小题给出的选项中,只有一项是符合题目要求的。
1.如图所示的几何体,其主视图是( )
A.
B.
C.
D.
2.若是一元二次方程的一个根,则的值为( )
A. B. C. D.
3.如图,直线,若,,,则的长为( )
A.
B.
C.
D.
4.如图,菱形的边长,对角线,则菱形的面积为( )
A.
B.
C.
D.
5.一个口袋中有红球、白球共个,这些球除颜色外都相同,将口袋中的球搅拌均匀,从中随机摸出一个球,记下它的颜色后再放回口袋中不断重复这一过程,共摸了次球,发现有次摸到红球,请估计这个口袋中红球的数量最有可能是( )
A. B. C. D.
6.如图,公园原有一块正方形空地,后来从这块空地上划出部分区域栽种鲜花,原空地一边减少了,另一边减少了,剩余空地面积为,设原正方形空地的边长是,根据题意,可列方程为( )
A.
B.
C.
D.
7.已知点,在反比例函数的图象上,则下列说法正确的是( )
A. 当时, B. 当时,
C. 当时, D. 当时,
8.如图,在平面直角坐标系中,的三个顶点,,的坐标分别为,,以原点为位似中心,作的位似图形,且与的相似比为:,点,,的对应点分别为,,,则点的坐标是( )
A. B.
C. 或 D. 或
二、填空题:本题共10小题,每小题4分,共40分。
9.若,则______.
10.已知关于的一元二次方程有两个相等的实数根,则 ______.
11.已知反比例函数的图象经过,两点,若点的坐标为,则点的坐标可能是______写一个即可.
12.如图,在正方形的对角线上取点使,连接,过点作交于点,则的大小为______.
13.如图,在中,,,,以点为圆心,长为半径画弧,交于点,再分别以,为圆心,大于长为半径画弧,两弧交于点,,作直线交于点,交于点,则的长为______.
14.若,是一元二次方程的两个实数根,则的值为______.
15.如图,在菱形中,,连接,点是线段上一点,过点作,,垂足分别为点,若,则的值为______.
16.如图,在平面直角坐标系中,直线与反比例函数的图象交于点,点在轴的负半轴上,连接若,的面积为,则的值为______.
17.如图所示两个矩形和,若矩形的周长是矩形的周长的倍,矩形的面积也是矩形的面积的倍,则称为矩形相对于矩形的“共比系数”若时,矩形相对于矩形的“共比系数”为,则 ______;若,均为正整数,则矩形相对于矩形的“共比系数”为的概率为______.
18.如图,在四边形中,,,对角线平分过点作于点,平分交于点,交于点若,,则的长为______.
三、解答题:本题共8小题,共78分。解答应写出文字说明,证明过程或演算步骤。
19.本小题分
计算:;
解方程:.
20.本小题分
随着气温日渐走低,成都的银杏也渐渐褪去青绿,悄然变黄为鼓励同学们利用课余时间走进成都街头巷尾,发现银杏之美丽,感受自然之神奇,某校随机对该校部分学生进行了“你心中的最美银杏打卡点”问卷调查问卷设置了四个选项:文殊院;青羊宫;百花潭公园;电子科技大学通过调查得到下列不完整的统计图请结合统计图,回答下列问题:
求本次调查中接受调查的学生人数;
补全条形统计图;
在选择的四名学生中,有名男生,名女生现随机抽取其中名同学担任“银杏使者”,请用列表或画树状图的方法,求抽到的名同学都为女生的概率.
21.本小题分
如图,三根木杆,,竖直立于地平面,点,,在同一条直线上,且每两根木杆之间的距离为米,即米,木杆,的影子分别为,.
在图、图两个示意图中,反映阳光下情形的是图______,反映灯光下情形的是图______;填图形序号
请在图中画出表示木杆的影长的线段;
已知木杆长为米,木杆长为米,木杆长为米,在图中测得木杆,的影长米,求木杆的影长.
22.本小题分
如图,在 中,,分别为,的中点,连接,,且.
求证:四边形是菱形;
如图,连接交于点,交于点,且,连接,.
求证:;
若,求的长.
23.本小题分
如图,在平面直角坐标系中,点坐标为,点坐标为,平移线段得线段,连接,反比例函数的图象经过点,交直线于,两点.
若,,求反比例函数的表达式;
试探究的值是否为定值,若是,请求出;若不是,请说明理由;
如图,取线段的中点,连接,若,求所在直线的表达式.
24.本小题分
“骑行安全最重要,安全头盔要戴好”年月日起,新修订的成都市非机动车管理条例正式实施,对驾驶非机动车闯红灯、不戴头盔、逆行等违法行为做出了规范据了解,某经销商以元个的价格购入一批头盔,按元个的价格销售一段时间后,连续两次对该头盔进行降价,两次降价后,该头盔的售价为元个若该经销商两次降价的百分率相同,求每次降价的百分率;
市场调研表明:当头盔售价为元个时,每月能够售出个,当售价每降元时,则月销量能增加个若要使月销售利润为元,则头盔的售价应为多少元?
25.本小题分
如图,在平面直角坐标系中,反比例函数图象上有,两点,其中点在点右侧,连接,,.
如图,设点坐标为,若,,且.
求的值;
若的面积为,求点的坐标;
如图,延长交反比例函数的图象于点,连接,点为上一点,连接并延长交于点若的面积与的面积相等,是否存在直线,使得点始终在该直线下方,若存在,请求出的最小值;若不存在,请说明理由.
26.本小题分
如图,在中,为边上一点,交于,延长,相交于点,.
求证:;
连接,若是以为腰的等腰三角形,,求的值;
如图,在中,,,,为直线下方一点,点关于直线的对称点恰好在的延长线上,连接,,若,求的长.
1.【答案】
2.【答案】
3.【答案】
4.【答案】
5.【答案】
6.【答案】
7.【答案】
8.【答案】
9.【答案】
10.【答案】
11.【答案】答案不唯一
12.【答案】
13.【答案】
14.【答案】
15.【答案】
16.【答案】
17.【答案】或
18.【答案】
19.【答案】解:原式
提取公因式得,
或,
,.
20.【答案】解:本次调查中接受调查的学生人数为人.
选择的人数为人.
补全条形统计图如图所示.
列表如下:
男 女 女 女
男 男,女 男,女 男,女
女 女,男 女,女 女,女
女 女,男 女,女 女,女
女 女,男 女,女 女,女
共有种等可能的结果,其中抽到的名同学都为女生的结果有种,
抽到的名同学都为女生的概率为.
21.【答案】
22.【答案】证明:四边形是平行四边形,
,,
,分别为,的中点,
,,
,
四边形是平行四边形,
,
,
,
四边形是菱形;
证明:,
,
四边形是菱形,
,,
,
,
,
,
,
;
解:,
∽,
,
,
,
设,,
,
,
,
,,
,
,
,
,
舍去负值,
.
23.【答案】解:当,时,,.
根据线段平移的性质,.
点坐标为.
由反比例函数表达式得.
反比例函数的表达式为.
如图,过点作轴的垂线交轴于点.
轴.
由平行线分线段成比例得:.
,,,.
.
点在反比例函数的图象上,同理可得点的坐标为.
.
.
.
.
,.
四边形是平行四边形.
.
.
故的值为定值.
设直线的函数表达式为,把、两点坐标代入得:
,解得.
直线的表达式为.
由于反比例函数表达式为,与直线函数表达式联立得:
.
整理得.
.
,.
点的坐标为也是线段的中点.
根据线段平移的性质可得点坐标为,则.
同理,由两点坐标根据待定系数法求得的解析式为:.
过点作轴,垂足为,过点作与延长线交于点,再过点作轴,垂足为.
,
.
在和中,,
.
∽.
.
,
点在直线上,
,
代入和得:,
整理得:.
又,则,代入上式得.
.
直线的解析式为.
24.【答案】解:设每次降价的百分率为,
根据题意得:,
解得或舍去,
每次降价的百分率为;
设头盔的售价应为元,
根据题意得:,
整理得,
解得或,
头盔的售价应为元或元.
25.【答案】解:,且,
,,
点坐标为,
;
过点作轴于点,过点作轴于点,
设点的坐标为,
,
,
,即,
整理可得:,
解得负值舍去,
点的坐标为;
连接,
,
,
,
,
为中点,
为中点,
,
点坐标为,
点坐标为,
反比例函数表达式为,
设点的坐标为,
点的坐标为,
点的坐标为,
,
,
点始终在直线的下方,
的最小值为.
26.【答案】证明:,
,
又,
,
∽,
,
,
,
;
解:,
设,,
在中,由勾股定理可得,
当时,
,
,
,
,
,
在和中,
,,
∽,
,
,
;
当时,
同理可得,
,
,
,
∽,
;
综上所述,的值为或;
如图,点关于直线的对称点恰好在的延长线上,
连接,延长交于点,过点作交延长线于点,连接,
点关于直线的对称点恰好在的延长线上,
,,
,
∽,
,
,,
,
设,,
,,
在和中,
,,
∽,
,
,
,
,
,
设,,则,,
,
在中,由勾股定理可得:,
整理可得:,
解得负值舍去,
,
在中,由勾股定理可得,
即.
第1页,共1页
同课章节目录
