21.2二次根式的乘除法课件
图片预览







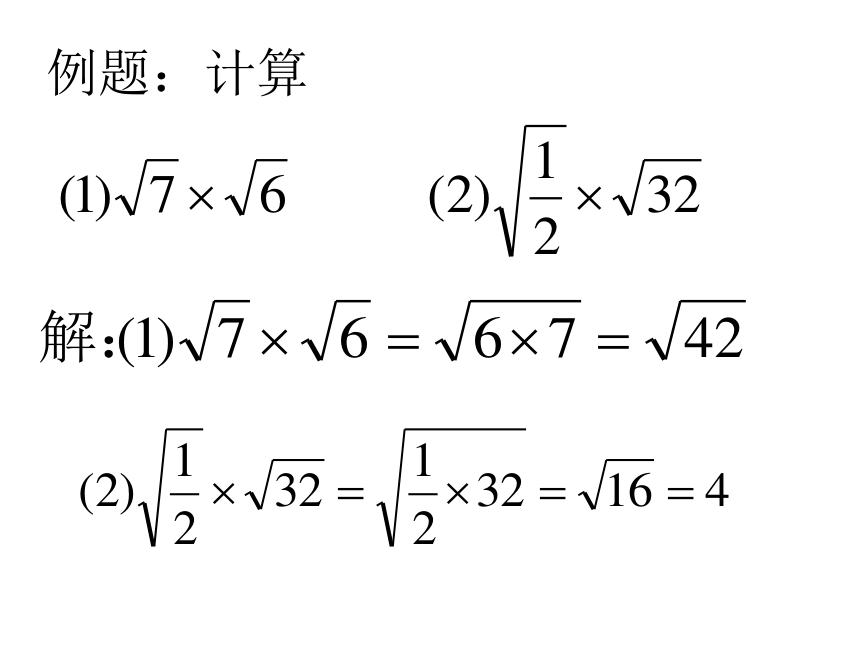
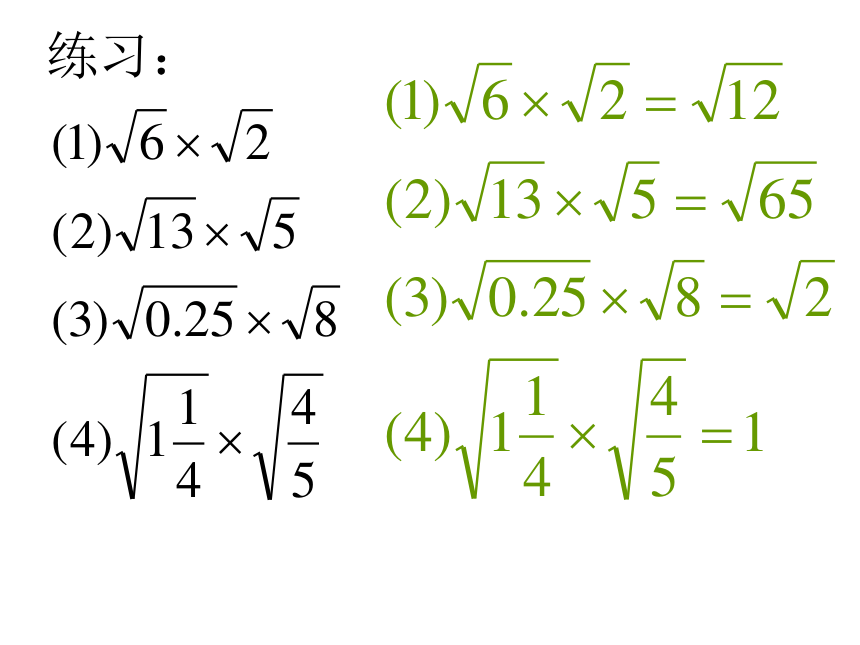



文档简介
课件55张PPT。华东师大版
九年级(上)数学教学课件华东师大版九年级第21章二次根式21.2 二次根式的乘除(第1课时)1、什么叫二次根式?下列各式哪些是二次根式?哪些不是?为什么?复习2、填空3、计算4、请同学们根据以上例子讨论、归纳总结出一般规律二次根式的乘法(a≥0,b≥0) 二次根式乘法运算规律公式 积的算术平方根,等于积中各因式的算术平方根的积。问题1: ?×(a≥0,b≥0)问题2: ?×××注意:(a≥0,b≥0)例题:计算练习:(a≥0,b≥0) 二次根式乘法运算规律公式的应用例题:化简:如何化简二次根式关键:将被开方数因式分解或
因数分解,使出现“完全平方数”
或“偶次方因式”化简:由上例可得以下规律:(a≥0,b≥0)练习:例题 化简:练习:练习1、化简如何化简二次根式关键:将被开方数因式分解或
因数分解,使出现“完全平方数”
或“偶次方因式”先计算,再化简化简:试一试2、化简例题3
如图,在△ABC中, ∠C=900, AC=10 cm, BC=24cm, AB2=AC2+BC2。求 : AB.练习3
一个直角三角形的两条直角边分别长 与 ,求这个直角三角形的面积。小结:乘法规律公式推广式:华东师大版九年级第21章二次根式21.2 二次根式的乘除(第2课时)复习提问1、二次根式的性质有哪些? 2、填空(1)当a , b ,成立。(2)(3)这是积的算术平方根的性质。复习提问二次根式的除法二、探讨( )=(1)(2)观察1、2小题的结果,它们有什么特点?(1)、(2)题结果相同。你能列出怎样的等式呢?即:这个等式用字母怎么表示呢?思考:等式中的a和b有没有条件的限制?请同学们用文字叙述该等式的意义。公式的逆用注意(1) 这里的被开方数是一个整式。(可以是多项式,也可以是单项式。) (2) 注意被开方数的取值范围。1、与积的算术平方根的性质比较:共同点:一个根号变成两个根号。区别:取值范围不同。商的算术平方根:2、理解和记忆商的算术平方根要注意的问题比较,得出结论练习一下:例3、化简:解:原式=练习:(填下列各题的解题步骤)解:原式==可以开方的一定要开方!化到最简!解:原式=遇到被开方数是小数先化成分数再化简! = =难度加深例4:化简三、请你帮忙: 小明在学习本节内容后,做一道化简题作业。第二天作业发下来后,小明知道做错了,可他百思不得其解,你能帮小明找出错的原因吗?解:原式=请大家从观察被开方数,想一想?分析:也就是说我们应该先把带分数化成假分数!再运用商的算术平方根的性质!很显然小明理解错带分数的意义正确解法:解:原式=总结:遇到被开方数是带分数,化带分数为假分数训练题: 四、练习单元(一)( ) ( )总结:商的算术平方根性质的运用一定要注意被开方数的取值范围。错C(二)填空(三)选择:① ( D)( )B所以本题选B②小结:请同学们小结一下本节课的内容:1、本节课学习了商的算术平方根的性质,我们要注意被开方数的取值范围。同时应该明确被开方数是整式。2、运用性质化简时应该注意结果要最简,如果被开方数是带分数要先化成假分数。然后再运用性质。3、从本节的学习同学们要学会灵活运用数学知识,数学的形式是很优美也很灵活的,大家要不断探索,克服困难提高学习数学的能力。分析:要求 关键是求X、Y,
两个非负数相加和为0。也就是说它们要分别为0。解得:综合练习思考题1、已知x满足不等式3x+5≤0,求下面等式中的代数式M最简二次根式华东师大版九年级第21章二次根式21.2 二次根式的乘除(第3课时)满足下列条件的二次根式,叫做最简二次根式。
(1)被开方数中的因数是整数,因式是整式;
(2)被开方数中不含能开得尽方的因数或因式;
(3)分母中不含根号。
最简二次根式的定义判断下列各式是否为最简二次根式? (5) ( );(2) ( );(3) ( );(4) ( ); (1) ( );(6) ( );(7) ( );√×××××√辨析训练 1、把下列各式化成最简二次根式:练习2、计算(1) (2) 解(2):方法1:方法2:3、已知: ,如何求 与 的近似值?(结果保留两位有效数字)解: 例2 把下列各式化成最简二次根式:
(1) ;(2)解(1)(2) 把下列各式化成最简二次根式:
(1) (2)
(1)
(2)
(3) (4)
(3)
(4)练习二 把下列各式化成最简二次根式:
(1)
(2)
(3)
(4)强化训练这节你学到了什么?1.最简二次根式的概念.满足下列条件的二次根式,叫做最简二次根式。
(1)被开方数中的因数是整数,因式是整式;
(2)被开方数中不含能开得尽方的因数或因式;
(3)分母中不含根号。2.如何化二次根式为最简二次根式 .课堂小结:
九年级(上)数学教学课件华东师大版九年级第21章二次根式21.2 二次根式的乘除(第1课时)1、什么叫二次根式?下列各式哪些是二次根式?哪些不是?为什么?复习2、填空3、计算4、请同学们根据以上例子讨论、归纳总结出一般规律二次根式的乘法(a≥0,b≥0) 二次根式乘法运算规律公式 积的算术平方根,等于积中各因式的算术平方根的积。问题1: ?×(a≥0,b≥0)问题2: ?×××注意:(a≥0,b≥0)例题:计算练习:(a≥0,b≥0) 二次根式乘法运算规律公式的应用例题:化简:如何化简二次根式关键:将被开方数因式分解或
因数分解,使出现“完全平方数”
或“偶次方因式”化简:由上例可得以下规律:(a≥0,b≥0)练习:例题 化简:练习:练习1、化简如何化简二次根式关键:将被开方数因式分解或
因数分解,使出现“完全平方数”
或“偶次方因式”先计算,再化简化简:试一试2、化简例题3
如图,在△ABC中, ∠C=900, AC=10 cm, BC=24cm, AB2=AC2+BC2。求 : AB.练习3
一个直角三角形的两条直角边分别长 与 ,求这个直角三角形的面积。小结:乘法规律公式推广式:华东师大版九年级第21章二次根式21.2 二次根式的乘除(第2课时)复习提问1、二次根式的性质有哪些? 2、填空(1)当a , b ,成立。(2)(3)这是积的算术平方根的性质。复习提问二次根式的除法二、探讨( )=(1)(2)观察1、2小题的结果,它们有什么特点?(1)、(2)题结果相同。你能列出怎样的等式呢?即:这个等式用字母怎么表示呢?思考:等式中的a和b有没有条件的限制?请同学们用文字叙述该等式的意义。公式的逆用注意(1) 这里的被开方数是一个整式。(可以是多项式,也可以是单项式。) (2) 注意被开方数的取值范围。1、与积的算术平方根的性质比较:共同点:一个根号变成两个根号。区别:取值范围不同。商的算术平方根:2、理解和记忆商的算术平方根要注意的问题比较,得出结论练习一下:例3、化简:解:原式=练习:(填下列各题的解题步骤)解:原式==可以开方的一定要开方!化到最简!解:原式=遇到被开方数是小数先化成分数再化简! = =难度加深例4:化简三、请你帮忙: 小明在学习本节内容后,做一道化简题作业。第二天作业发下来后,小明知道做错了,可他百思不得其解,你能帮小明找出错的原因吗?解:原式=请大家从观察被开方数,想一想?分析:也就是说我们应该先把带分数化成假分数!再运用商的算术平方根的性质!很显然小明理解错带分数的意义正确解法:解:原式=总结:遇到被开方数是带分数,化带分数为假分数训练题: 四、练习单元(一)( ) ( )总结:商的算术平方根性质的运用一定要注意被开方数的取值范围。错C(二)填空(三)选择:① ( D)( )B所以本题选B②小结:请同学们小结一下本节课的内容:1、本节课学习了商的算术平方根的性质,我们要注意被开方数的取值范围。同时应该明确被开方数是整式。2、运用性质化简时应该注意结果要最简,如果被开方数是带分数要先化成假分数。然后再运用性质。3、从本节的学习同学们要学会灵活运用数学知识,数学的形式是很优美也很灵活的,大家要不断探索,克服困难提高学习数学的能力。分析:要求 关键是求X、Y,
两个非负数相加和为0。也就是说它们要分别为0。解得:综合练习思考题1、已知x满足不等式3x+5≤0,求下面等式中的代数式M最简二次根式华东师大版九年级第21章二次根式21.2 二次根式的乘除(第3课时)满足下列条件的二次根式,叫做最简二次根式。
(1)被开方数中的因数是整数,因式是整式;
(2)被开方数中不含能开得尽方的因数或因式;
(3)分母中不含根号。
最简二次根式的定义判断下列各式是否为最简二次根式? (5) ( );(2) ( );(3) ( );(4) ( ); (1) ( );(6) ( );(7) ( );√×××××√辨析训练 1、把下列各式化成最简二次根式:练习2、计算(1) (2) 解(2):方法1:方法2:3、已知: ,如何求 与 的近似值?(结果保留两位有效数字)解: 例2 把下列各式化成最简二次根式:
(1) ;(2)解(1)(2) 把下列各式化成最简二次根式:
(1) (2)
(1)
(2)
(3) (4)
(3)
(4)练习二 把下列各式化成最简二次根式:
(1)
(2)
(3)
(4)强化训练这节你学到了什么?1.最简二次根式的概念.满足下列条件的二次根式,叫做最简二次根式。
(1)被开方数中的因数是整数,因式是整式;
(2)被开方数中不含能开得尽方的因数或因式;
(3)分母中不含根号。2.如何化二次根式为最简二次根式 .课堂小结:
