内蒙古包头市昆都仑区2024-2025学年八年级(上)期末数学试卷(含答案)
文档属性
| 名称 | 内蒙古包头市昆都仑区2024-2025学年八年级(上)期末数学试卷(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 154.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-01-24 00:00:00 | ||
图片预览



文档简介
内蒙古包头市昆都仑区2024-2025学年八年级(上)期末数学试卷
第I卷(选择题)
一、选择题:本题共10小题,每小题3分,共30分。在每小题给出的选项中,只有一项是符合题目要求的。
1.实数的算术平方根是( )
A. B. C. D.
2.下列各组数分别为一个三角形三边的长,其中能构成直角三角形的一组是( )
A. ,, B. ,, C. ,, D. ,,
3.如图,正方形内的数字代表所在正方形的面积,则所在的正方形的面积为( )
A.
B.
C.
D.
4.在平面直角坐标系中,点,,则的长为( )
A. B. C. D.
5.如图,是一片树叶标本,将其放在平面直角坐标系中,表示叶片尖端,两点的坐标分别为,,则叶柄底部点的坐标为( )
A.
B.
C.
D.
6.已知一次函数的图象如图所示,则,的取值范围是( )
A. ,
B. ,
C. ,
D. ,
7.对于二元一次方程组,将代入,消去可以得到( )
A. B. C. D.
8.某商场对上周末某品牌运动服的销售情况进行了统计,如下表所示:经理决定本周进货时多进一些红色的,可用来解释这一现象的统计知识是( )
颜色 黄色 绿色 白色 紫色 红色
数量件
A. 平均数 B. 中位数 C. 众数 D. 平均数与中位数
9.已知,,,则、、的大小关系是( )
A. B. C. D.
10.若正比例函数的图象经过点,则这个图象必经过点( )
A. B. C. D.
第II卷(非选择题)
二、填空题:本题共5小题,每小题3分,共15分。
11.一把直尺和一个含角的直角三角板按如图方式放置,若,则 ______.
12.已知关于,的方程组的解满足,则的值为______.
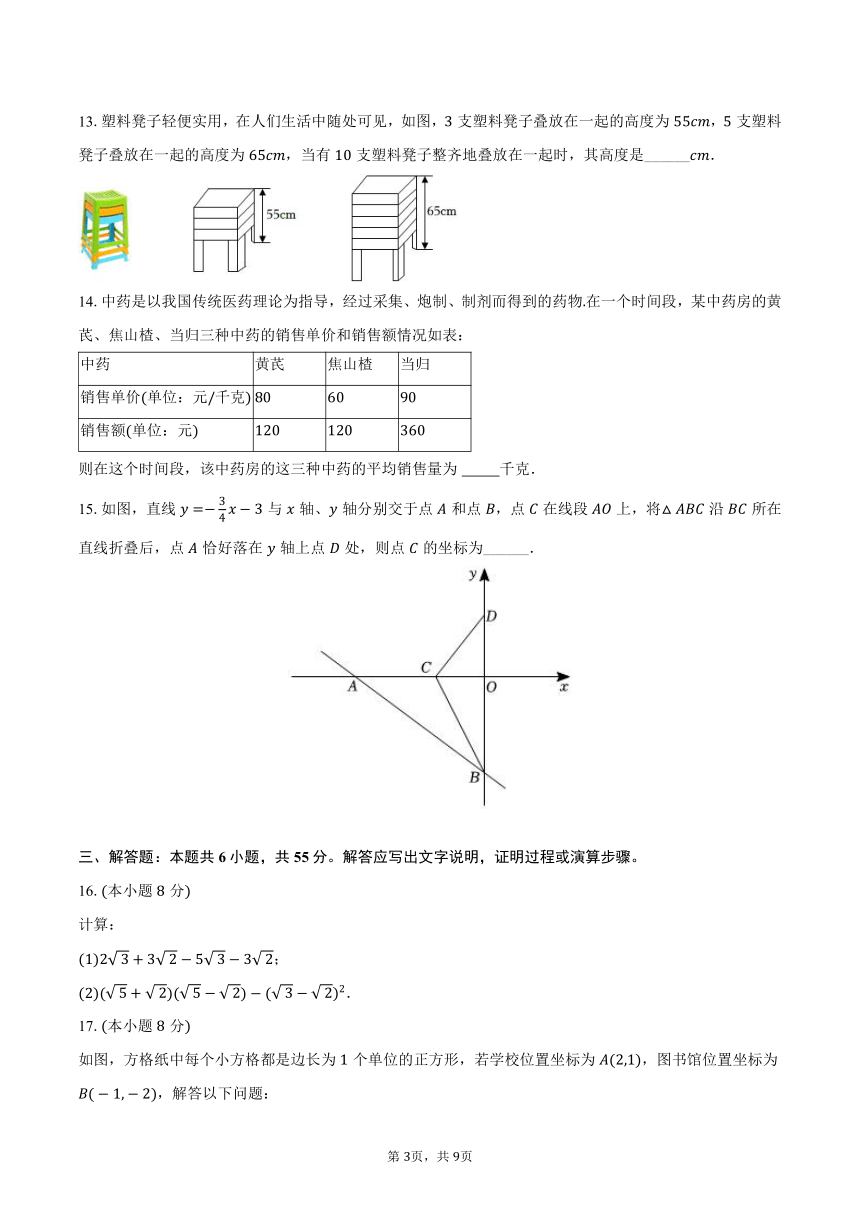
13.塑料凳子轻便实用,在人们生活中随处可见,如图,支塑料凳子叠放在一起的高度为,支塑料凳子叠放在一起的高度为,当有支塑料凳子整齐地叠放在一起时,其高度是______.
14.中药是以我国传统医药理论为指导,经过采集、炮制、制剂而得到的药物在一个时间段,某中药房的黄芪、焦山楂、当归三种中药的销售单价和销售额情况如表:
中药 黄芪 焦山楂 当归
销售单价单位:元千克
销售额单位:元
则在这个时间段,该中药房的这三种中药的平均销售量为 千克.
15.如图,直线与轴、轴分别交于点和点,点在线段上,将沿所在直线折叠后,点恰好落在轴上点处,则点的坐标为______.
三、解答题:本题共6小题,共55分。解答应写出文字说明,证明过程或演算步骤。
16.本小题分
计算:
;
.
17.本小题分
如图,方格纸中每个小方格都是边长为个单位的正方形,若学校位置坐标为,图书馆位置坐标为,解答以下问题:
在图中标出平面直角坐标系的原点,并建立直角坐标系;
若体育馆位置坐标为,请在坐标系中标出体育馆的位置;
顺次连接学校、图书馆、体育馆,得到,求的面积.
18.本小题分
如图,直线分别与直线,相交于点和点,平分,平分,并且说出图中哪些直线互相平行,并说明理由,
19.本小题分
年月日是第个世界气象日,今年世界气象日的主题是“气候行动最前线”学校借此机会举行气象知识竞赛,要求每班选派名同学参加满分分,成绩为整数比赛结束后,竞赛组委会将八年级甲、乙两班参赛同学的成绩汇总并绘制成下面的条形统计图.
两个班的成绩分析如表:
班级 平均分 中位数 方差
甲班
乙班
填空: ______, ______.
参赛同学小婷说:“这次竞赛我得了分,在我们班中排名属中游略偏上”观察上表可知,小婷是______班的学生;填“甲”或“乙”
你认为甲乙两班哪个班成绩更好?请结合上表中的两种统计量说明理由.
20.本小题分
如图,将长方形沿直线折叠,顶点恰好落在边上点处,已知,.
求的长;
求图中阴影部分的面积.
21.本小题分
综合与实践:
为带动乡村经济发展,某县农业基地采摘园在草莓成熟季节对当地城乡居民开放,这样一来,市民周末也多了一个亲子活动的好去处甲、乙两家草莓采摘园的草莓销售价格相同,现为扩大销量,实行的采摘方案如下:
甲采摘园的采摘方案:每位游客进园需购买门票,采摘的草莓按七折优惠销售;
乙采摘园的采摘方案:每位游客进园无需购买门票,采摘的草莓按售价销售,不优惠.
设采摘期间每位游客的草莓采摘量为单位:千克,在甲、乙采摘园所需总费用分别为,单位:元,其函数图象如图所示.
分别求出,与之间的函数关系式不需要写出的自变量的取值范围.
求点的坐标,并解释点表示的实际意义.
小轩准备周末去采摘园采摘草莓,根据函数图象,请直接写出选择哪个采摘园更合算.
1.【答案】
2.【答案】
3.【答案】
4.【答案】
5.【答案】
6.【答案】
7.【答案】
8.【答案】
9.【答案】
10.【答案】
11.【答案】
12.【答案】
13.【答案】
14.【答案】
15.【答案】
16.【答案】解:原式;
原式
.
17.【答案】解:如图,点即为原点,
如图,点即为所求;
.
18.【答案】解:,.
理由:平分,平分,
,,
,
,,
,.
19.【答案】 甲
20.【答案】解:由折叠可知和关于成轴对称,
故AF,.
所以;
设,则.
在中,由勾股定理,得.
解得,即;
.
所以阴影部分的面积为:
21.【答案】解:由题意,设,,
的函数图象经过点,
,可知采摘的草莓的售价是元千克,
,
的函数图象经过点,可知,
,
故和与之间的函数解析式分别是,;
根据函数图象可知,点是与函数图象的交点,则,
联立与,得
解得,
将代入中,得,
点的坐标为,
点的实际意义是:当游客的草莓采摘量为千克时,选择甲、乙两个采摘园所需总费用相同,均为元;
由图象可知,当小明的草莓采摘量小于千克时,在下方,选择乙采摘园更划算;
当小明的草莓采摘量为千克时,,选择甲、乙两个采摘园所需总费用相同;
当小明的草莓采摘量大于千克时,在下方,选择甲采摘园更划算.
第1页,共1页
第I卷(选择题)
一、选择题:本题共10小题,每小题3分,共30分。在每小题给出的选项中,只有一项是符合题目要求的。
1.实数的算术平方根是( )
A. B. C. D.
2.下列各组数分别为一个三角形三边的长,其中能构成直角三角形的一组是( )
A. ,, B. ,, C. ,, D. ,,
3.如图,正方形内的数字代表所在正方形的面积,则所在的正方形的面积为( )
A.
B.
C.
D.
4.在平面直角坐标系中,点,,则的长为( )
A. B. C. D.
5.如图,是一片树叶标本,将其放在平面直角坐标系中,表示叶片尖端,两点的坐标分别为,,则叶柄底部点的坐标为( )
A.
B.
C.
D.
6.已知一次函数的图象如图所示,则,的取值范围是( )
A. ,
B. ,
C. ,
D. ,
7.对于二元一次方程组,将代入,消去可以得到( )
A. B. C. D.
8.某商场对上周末某品牌运动服的销售情况进行了统计,如下表所示:经理决定本周进货时多进一些红色的,可用来解释这一现象的统计知识是( )
颜色 黄色 绿色 白色 紫色 红色
数量件
A. 平均数 B. 中位数 C. 众数 D. 平均数与中位数
9.已知,,,则、、的大小关系是( )
A. B. C. D.
10.若正比例函数的图象经过点,则这个图象必经过点( )
A. B. C. D.
第II卷(非选择题)
二、填空题:本题共5小题,每小题3分,共15分。
11.一把直尺和一个含角的直角三角板按如图方式放置,若,则 ______.
12.已知关于,的方程组的解满足,则的值为______.
13.塑料凳子轻便实用,在人们生活中随处可见,如图,支塑料凳子叠放在一起的高度为,支塑料凳子叠放在一起的高度为,当有支塑料凳子整齐地叠放在一起时,其高度是______.
14.中药是以我国传统医药理论为指导,经过采集、炮制、制剂而得到的药物在一个时间段,某中药房的黄芪、焦山楂、当归三种中药的销售单价和销售额情况如表:
中药 黄芪 焦山楂 当归
销售单价单位:元千克
销售额单位:元
则在这个时间段,该中药房的这三种中药的平均销售量为 千克.
15.如图,直线与轴、轴分别交于点和点,点在线段上,将沿所在直线折叠后,点恰好落在轴上点处,则点的坐标为______.
三、解答题:本题共6小题,共55分。解答应写出文字说明,证明过程或演算步骤。
16.本小题分
计算:
;
.
17.本小题分
如图,方格纸中每个小方格都是边长为个单位的正方形,若学校位置坐标为,图书馆位置坐标为,解答以下问题:
在图中标出平面直角坐标系的原点,并建立直角坐标系;
若体育馆位置坐标为,请在坐标系中标出体育馆的位置;
顺次连接学校、图书馆、体育馆,得到,求的面积.
18.本小题分
如图,直线分别与直线,相交于点和点,平分,平分,并且说出图中哪些直线互相平行,并说明理由,
19.本小题分
年月日是第个世界气象日,今年世界气象日的主题是“气候行动最前线”学校借此机会举行气象知识竞赛,要求每班选派名同学参加满分分,成绩为整数比赛结束后,竞赛组委会将八年级甲、乙两班参赛同学的成绩汇总并绘制成下面的条形统计图.
两个班的成绩分析如表:
班级 平均分 中位数 方差
甲班
乙班
填空: ______, ______.
参赛同学小婷说:“这次竞赛我得了分,在我们班中排名属中游略偏上”观察上表可知,小婷是______班的学生;填“甲”或“乙”
你认为甲乙两班哪个班成绩更好?请结合上表中的两种统计量说明理由.
20.本小题分
如图,将长方形沿直线折叠,顶点恰好落在边上点处,已知,.
求的长;
求图中阴影部分的面积.
21.本小题分
综合与实践:
为带动乡村经济发展,某县农业基地采摘园在草莓成熟季节对当地城乡居民开放,这样一来,市民周末也多了一个亲子活动的好去处甲、乙两家草莓采摘园的草莓销售价格相同,现为扩大销量,实行的采摘方案如下:
甲采摘园的采摘方案:每位游客进园需购买门票,采摘的草莓按七折优惠销售;
乙采摘园的采摘方案:每位游客进园无需购买门票,采摘的草莓按售价销售,不优惠.
设采摘期间每位游客的草莓采摘量为单位:千克,在甲、乙采摘园所需总费用分别为,单位:元,其函数图象如图所示.
分别求出,与之间的函数关系式不需要写出的自变量的取值范围.
求点的坐标,并解释点表示的实际意义.
小轩准备周末去采摘园采摘草莓,根据函数图象,请直接写出选择哪个采摘园更合算.
1.【答案】
2.【答案】
3.【答案】
4.【答案】
5.【答案】
6.【答案】
7.【答案】
8.【答案】
9.【答案】
10.【答案】
11.【答案】
12.【答案】
13.【答案】
14.【答案】
15.【答案】
16.【答案】解:原式;
原式
.
17.【答案】解:如图,点即为原点,
如图,点即为所求;
.
18.【答案】解:,.
理由:平分,平分,
,,
,
,,
,.
19.【答案】 甲
20.【答案】解:由折叠可知和关于成轴对称,
故AF,.
所以;
设,则.
在中,由勾股定理,得.
解得,即;
.
所以阴影部分的面积为:
21.【答案】解:由题意,设,,
的函数图象经过点,
,可知采摘的草莓的售价是元千克,
,
的函数图象经过点,可知,
,
故和与之间的函数解析式分别是,;
根据函数图象可知,点是与函数图象的交点,则,
联立与,得
解得,
将代入中,得,
点的坐标为,
点的实际意义是:当游客的草莓采摘量为千克时,选择甲、乙两个采摘园所需总费用相同,均为元;
由图象可知,当小明的草莓采摘量小于千克时,在下方,选择乙采摘园更划算;
当小明的草莓采摘量为千克时,,选择甲、乙两个采摘园所需总费用相同;
当小明的草莓采摘量大于千克时,在下方,选择甲采摘园更划算.
第1页,共1页
同课章节目录
