期末能力提升卷(含解析)-2024-2025学年数学九年级上册人教版
文档属性
| 名称 | 期末能力提升卷(含解析)-2024-2025学年数学九年级上册人教版 |  | |
| 格式 | docx | ||
| 文件大小 | 733.0KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-01-23 19:30:43 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
期末能力提升卷-2024-2025学年数学九年级上册人教版
一.选择题(共8小题)
1.(2023秋 四平期末)下列关于x的方程中,一定属于一元二次方程的是( )
A.ax2﹣2x+3=0 B.x2+9=0
C. D.x2+2y+6=0
2.(2023秋 南通期末)函数y=x2﹣4x+3图象顶点坐标是( )
A.(2,﹣1) B.(﹣2,1) C.(﹣2,﹣1) D.(2,1)
3.(2023秋 兖州区期末)剪纸艺术是最古老的中国民间艺术之一,先后入选中国国家级非物质文化遗产名录和人类非物质文化遗产代表作名录.以下剪纸中,为中心对称图形的是( )
A. B.
C. D.
4.(2023秋 宿迁期末)已知⊙O的半径为3,点P是直线l上的一点,OP=3,则直线l与⊙O的位置关系是( )
A.相离 B.相切
C.相交 D.相切或相交
5.(2022秋 宛城区校级期末)不透明的袋子中装有红、绿小球各一个,除颜色外两个小球无其他差别,从中随机摸出一个小球,放回并摇匀,再从中随机摸出一个小球,那么第一次摸到红球、第二次摸到绿球的概率是( )
A. B. C. D.
6.(2023秋 延长县校级期末)若关于x的一元二次方程(m﹣1)x2﹣mx+1=0有两个相等的实数根,则m的值是( )
A.﹣2 B.﹣1 C.1 D.2
7.(2023秋 交口县期末)如图,BC是⊙O的切线,点B是切点,连接CO交⊙O于点D,延长CO交⊙O于点A,连接AB,若∠C=30°,OD=2,则AB的长为( )
A. B. C. D.
8.(2023秋 荣昌区校级期末)如图,二次函数y=ax2+bx+c(a≠0)的图象经过点,对称轴为直线x=1,下列结论:①abc<0;②a﹣2b+4c=0;③2a+b>0;④a+b≤m(am+b)(其中m≠1);⑤b﹣c>0;正确的结论有( )
A.1个 B.3个 C.2个 D.4个
二.填空题(共8小题)
9.(2023秋 沈河区校级期末)关于x的一元二次方程x2+3x+k=0有一个根为x=2,则k的值为 .
10.(2023秋 东西湖区期末)在平面直角坐标系中,点(4,﹣5)关于原点的对称点的坐标是 .
11.(2023秋 大观区校级期末)如图,一下水管道横截面为圆形,直径为260cm,下雨前水面宽为100cm,一场大雨过后,水面宽为240cm,则水位上升 cm.
12.(2023秋 洛阳期末)如图,顺次连接等边三角形三边中点得到四个全等等边三角形.任意给其中两个涂色,涂色部分正好是菱形的概率是 .
13.(2023秋 绥中县期末)飞机着陆后滑行的距离S(m)关于滑行时间t(s)的函数解析式是S=﹣1.5t2+60t,飞机着陆后滑行 m才能停下来.
14.(2023秋 甘井子区校级期末)如图,已知⊙O的半径为2,AC与⊙O相切,连接AO并延长,交⊙O于点B,过点C作CD⊥AB,交⊙O于点D,连接BD,若∠A=30°,则弦BD的长为 .
15.(2023秋 连云港期末)如图,在平面直角坐标系中,正六边形OABCDE边长是6,则它的外接圆心P的坐标是 .
16.(2023秋 大观区校级期末)将抛物线y=﹣x2向右平移后,所得新抛物线的顶点是B,新抛物线与原抛物线交于点A(如图所示),连接OA、AB,如果△AOB是等边三角形,则OB的长为 .
三.解答题(共8小题)
17.(2023秋 琼海校级期末)解方程:
(1)x2﹣2x﹣2=0;
(2).
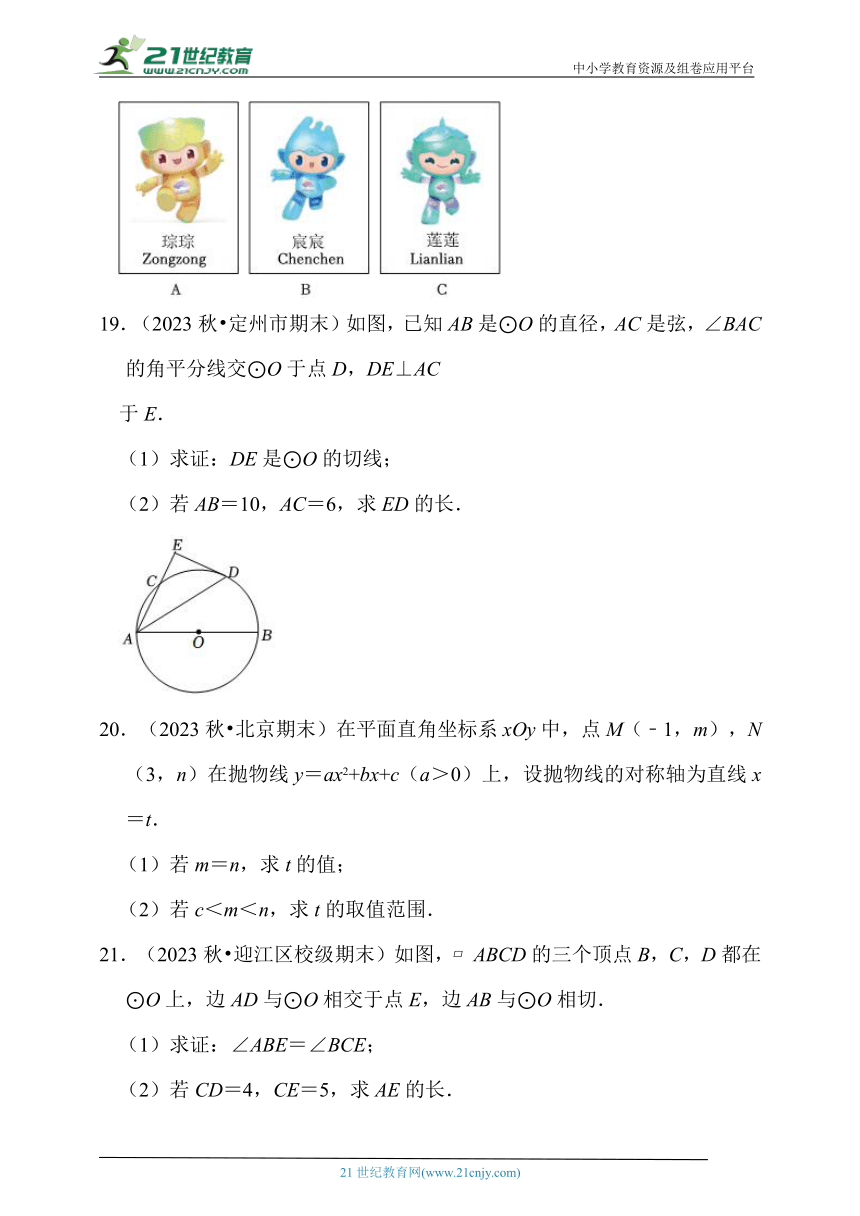
18.(2023秋 双阳区期末)杭州第19届亚运会吉祥物“江南忆”,具体指A.琮琮、B.宸宸、C.莲莲.如图是三张吉祥物的不透明卡片(卡片除内容外,其余均相同).将这三张卡片背面朝上洗匀放好,小李同学从这三张卡片中随机抽取一张后,再从剩余的两张卡片中随机抽取一张,请用树状图法或列表法,求两次抽到卡片恰好是琮琮和宸宸的概率.
19.(2023秋 定州市期末)如图,已知AB是⊙O的直径,AC是弦,∠BAC的角平分线交⊙O于点D,DE⊥AC
于E.
(1)求证:DE是⊙O的切线;
(2)若AB=10,AC=6,求ED的长.
20.(2023秋 北京期末)在平面直角坐标系xOy中,点M(﹣1,m),N(3,n)在抛物线y=ax2+bx+c(a>0)上,设抛物线的对称轴为直线x=t.
(1)若m=n,求t的值;
(2)若c<m<n,求t的取值范围.
21.(2023秋 迎江区校级期末)如图, ABCD的三个顶点B,C,D都在⊙O上,边AD与⊙O相交于点E,边AB与⊙O相切.
(1)求证:∠ABE=∠BCE;
(2)若CD=4,CE=5,求AE的长.
22.(2023秋 奇台县校级期末)为助力脱贫攻坚,某村在“农村淘宝网店”上销售该村优质农产品,该网店于今年一月底收购一批每袋进价25元的农产品,售价为每袋40元,二月份销售192袋,三、四月该商品十分畅销,销售量持续走高,在售价不变的基础上,四月份的销售量达到300袋.
(1)求三、四这两个月销售量的月平均增长率;
(2)该网店五月降价促销,经调查发现,若该农产品每袋降价1元,销售量可增加5袋,当农产品每袋降价多少元时,这种农产品在五月份可获利3250元?
23.(2023秋 雁塔区校级期末)某校在元旦活动时布置教室,如图1,教室两墙AB、CD之间悬挂一条近似抛物线y=ax2﹣x+3的彩带,如图2,已知AB=CD,BD=6米.
(1)如图2,两墙AB、CD的高度是 米,抛物线的顶点坐标为 ;
(2)如图3,为了避免彩带太低影响人员走动且考虑美观,现把彩带从点M、N处用细线吊在天花板上,形成抛物线F1,F2,F3;点M到墙AB距离为2.5米,抛物线F1的最低点距墙AB的距离为2米且离地面2米,求点M到地面的距离.
24.(2023秋 呼兰区校级期末)如图1,在平面直角坐标系中,O为坐标原点,抛物线y=x2+bx+c与x轴负半轴交于点B,与x轴正半轴于点A(3,0),交y轴于点C,连接AC,tan∠OAC=1.
(1)求抛物线的解析式;
(2)如图2,点P为第三象限抛物线上一点,连接PB,PO,若设△POB的面积为S,点P的横坐标为t,求S与t的函数关系式(不要求写出自变量t的取值范围);
(3)在(2)的条件下,如图3,过点P作PE⊥x轴于点E,点K为抛物线的顶点,连接BK交PE于点F,点D为AK上一点,BF=DK,连接DF,若∠EBF﹣∠DFK=45°,求点P的坐标.
期末能力提升卷-2024-2025学年数学九年级上册人教版
参考答案与试题解析
题号 1 2 3 4 5 6 7 8
答案 B A C D A D C A
一.选择题(共8小题)
1.(2023秋 四平期末)下列关于x的方程中,一定属于一元二次方程的是( )
A.ax2﹣2x+3=0 B.x2+9=0
C. D.x2+2y+6=0
【解答】A、ax2﹣2x+3=0,该方程的未知数的二次项系数是a,当a=0时不是一元二次方程,故本选项错误,不符合题意;
B、x2+9=0,该方程符合一元二次方程的定义,故本选项正确,符合题意;
C、该方程是分式方程,不是一元二次方程,故本选项错误,不符合题意;
D、x2+2y+6=0,该方程有两个未知数,该方程不是一元二次方程,故本选项错误,不符合题意.
故选:B.
2.(2023秋 南通期末)函数y=x2﹣4x+3图象顶点坐标是( )
A.(2,﹣1) B.(﹣2,1) C.(﹣2,﹣1) D.(2,1)
【解答】解:∵y=x2﹣4x+3,
=(x2﹣4x+4)﹣4+3,
=(x﹣2)2﹣1,
∴顶点坐标是(2,﹣1).
故选:A.
3.(2023秋 兖州区期末)剪纸艺术是最古老的中国民间艺术之一,先后入选中国国家级非物质文化遗产名录和人类非物质文化遗产代表作名录.以下剪纸中,为中心对称图形的是( )
A. B.
C. D.
【解答】解:A.该图形不是中心对称图形,故此选项不合题意;
B.该图形不是中心对称图形,故此选项不合题意;
C.该图形是中心对称图形,故此选项符合题意;
D.该图形不是中心对称图形,故此选项不合题意.
故选:C.
4.(2023秋 宿迁期末)已知⊙O的半径为3,点P是直线l上的一点,OP=3,则直线l与⊙O的位置关系是( )
A.相离 B.相切
C.相交 D.相切或相交
【解答】解:分为两种情况:①如图1,当OP⊥直线l时,此时直线l与⊙O的位置关系是相切;
②如图2,当OP和直线l不垂直时,此时直线l与⊙O相交;
所以直线l与⊙O的位置关系是相切或相交,
故选:D.
5.(2022秋 宛城区校级期末)不透明的袋子中装有红、绿小球各一个,除颜色外两个小球无其他差别,从中随机摸出一个小球,放回并摇匀,再从中随机摸出一个小球,那么第一次摸到红球、第二次摸到绿球的概率是( )
A. B. C. D.
【解答】解:列表如下:
红 绿
红 (红,红) (绿,红)
绿 (红,绿) (绿,绿)
所有等可能的情况有4种,其中第一次摸到红球、第二次摸到绿球的有1种情况,
所以第一次摸到红球、第二次摸到绿球的概率为,
故选:A.
6.(2023秋 延长县校级期末)若关于x的一元二次方程(m﹣1)x2﹣mx+1=0有两个相等的实数根,则m的值是( )
A.﹣2 B.﹣1 C.1 D.2
【解答】解:∵关于x的一元二次方程(m﹣1)x2﹣mx+1=0有两个相等的实数根,
∴Δ=b2﹣4ac=(﹣m)2﹣4×(m﹣1)=(m﹣2)2=0,且m﹣1≠0,
解得:m=2,
故选:D.
7.(2023秋 交口县期末)如图,BC是⊙O的切线,点B是切点,连接CO交⊙O于点D,延长CO交⊙O于点A,连接AB,若∠C=30°,OD=2,则AB的长为( )
A. B. C. D.
【解答】解:连接OB、DB,则OB=OD=2,
∵AD是⊙O的直径,
∴∠ABD=90°,AD=2OD=4,
∵BC与⊙O相切于点B,
∴BC⊥OB,
∴∠OBC=90°,
∵∠C=30°,
∴∠BOC=60°,
∴△BOD是等边三角形,
∴BD=OD=2,
∴AB2,
故选:C.
8.(2023秋 荣昌区校级期末)如图,二次函数y=ax2+bx+c(a≠0)的图象经过点,对称轴为直线x=1,下列结论:①abc<0;②a﹣2b+4c=0;③2a+b>0;④a+b≤m(am+b)(其中m≠1);⑤b﹣c>0;正确的结论有( )
A.1个 B.3个 C.2个 D.4个
【解答】解:①二次函数的图象开口向上,a>0,函数的对称轴在y轴右侧,则ab<0,而c<0,故abc>0,故①错误,不符合题意;
②将点代入函数表达式得:a﹣2b+4c=0,故②正确,符合题意;
③函数的对称轴为直线,即b=﹣2a,故2a+b=0,故③错误,不符合题意;
④当x=1时,函数取得最小值,又m≠1,则a+b+c<m(am+b)+c,即a+b<m(am+b),故④错误,不符合题意;
⑤由②③得:a﹣2b+4c=0,b=﹣2a,则,故,故⑤错误,不符合题意;
综上,②正确.
故选:A.
二.填空题(共8小题)
9.(2023秋 沈河区校级期末)关于x的一元二次方程x2+3x+k=0有一个根为x=2,则k的值为 ﹣10 .
【解答】解:∵x的一元二次方程x2+3x+k=0有一个根为x=2,
∴4+6+k=0,
解得k=﹣10.
故答案为:﹣10.
10.(2023秋 东西湖区期末)在平面直角坐标系中,点(4,﹣5)关于原点的对称点的坐标是 (﹣4,5) .
【解答】解:点(4,﹣5)关于原点的对称点的坐标是(﹣4,5),
故答案为:(﹣4,5).
11.(2023秋 大观区校级期末)如图,一下水管道横截面为圆形,直径为260cm,下雨前水面宽为100cm,一场大雨过后,水面宽为240cm,则水位上升 170或70 cm.
【解答】解:作半径OD⊥AB于C,连接OB,
由垂径定理得:BCAB=50cm,
在Rt△OBC中,OC120cm,
当水位上升到圆心以下,水面宽240cm时,
则OC′50cm,
水面上升的高度为:120﹣50=70cm;
当水位上升到圆心以上时,水面上升的高度为:120+50=170cm,
综上可得,水面上升的高度为170cm或70cm.
故答案为:170或70.
12.(2023秋 洛阳期末)如图,顺次连接等边三角形三边中点得到四个全等等边三角形.任意给其中两个涂色,涂色部分正好是菱形的概率是 .
【解答】解:∵任意给其中两个涂色,涂色部分正好是菱形的有3个,
∴涂色部分正好是菱形的概率是,
故答案为:.
13.(2023秋 绥中县期末)飞机着陆后滑行的距离S(m)关于滑行时间t(s)的函数解析式是S=﹣1.5t2+60t,飞机着陆后滑行 600 m才能停下来.
【解答】解:由题意,
S=﹣1.5t2+60t,
=﹣1.5(t2﹣40t+400﹣400)
=﹣1.5(t﹣20)2+600,
即当飞机着陆后滑行600m才能停下来时,飞机才能停下来.
故答案为:600.
14.(2023秋 甘井子区校级期末)如图,已知⊙O的半径为2,AC与⊙O相切,连接AO并延长,交⊙O于点B,过点C作CD⊥AB,交⊙O于点D,连接BD,若∠A=30°,则弦BD的长为 2 .
【解答】解:设AB交CD于E,交⊙O于F,连接OC、OD,如图,
∵AC与⊙O相切,
∴OC⊥AC,
∴∠OCA=90°,
∴∠AOC=90°﹣∠A=90°﹣30°=60°,
∵CD⊥AB,
∴,DE=CE,
∴∠DOF=∠COF=60°,
∴∠B∠DOF=30°,
在Rt△OCE中,∵OEOC=1,
∴CEOE,
∴DE,
在Rt△BDE中,BD=2DE=2.
故答案为:2.
15.(2023秋 连云港期末)如图,在平面直角坐标系中,正六边形OABCDE边长是6,则它的外接圆心P的坐标是 (3,3) .
【解答】解:连接PA,PO,
∵正六边形OABCDE的外接圆心是P,
∴∠OPA60°,PO=PA,
∴△POA是等边三角形,
∴PO=PA=OA=6,
过P作PH⊥OA于H,则∠OPH∠OPA=30°,OHOA=3,
∴PH3,
∴P的坐标是(3,3),
故答案为:(3,3).
16.(2023秋 大观区校级期末)将抛物线y=﹣x2向右平移后,所得新抛物线的顶点是B,新抛物线与原抛物线交于点A(如图所示),连接OA、AB,如果△AOB是等边三角形,则OB的长为 2 .
【解答】解:过A作AC⊥x轴于点C,
∵点A在抛物线y=﹣x2上,
∴设A(m,﹣m2),
∵△AOB是等边三角形,
∴BC=OC=m,,
∴或m=0(舍去),
∴,
故答案为:.
三.解答题(共8小题)
17.(2023秋 琼海校级期末)解方程:
(1)x2﹣2x﹣2=0;
(2).
【解答】解:(1)x2﹣2x﹣2=0,
移项得x2﹣2x=2,
配方得x2﹣2x+1=2+1,即(x+1)2=3,
开方得,
解得;;
(2),
去分母,得
m﹣4+m+2=0,
解得m=1,
经检验,m=1是原方程的根.
18.(2023秋 双阳区期末)杭州第19届亚运会吉祥物“江南忆”,具体指A.琮琮、B.宸宸、C.莲莲.如图是三张吉祥物的不透明卡片(卡片除内容外,其余均相同).将这三张卡片背面朝上洗匀放好,小李同学从这三张卡片中随机抽取一张后,再从剩余的两张卡片中随机抽取一张,请用树状图法或列表法,求两次抽到卡片恰好是琮琮和宸宸的概率.
【解答】解:画树状图如下:
共有6种等可能的结果,其中两次抽到卡片恰好是琮琮和宸宸有2种结果,
所以两次抽取的卡片上都是莲莲的概率为.
19.(2023秋 定州市期末)如图,已知AB是⊙O的直径,AC是弦,∠BAC的角平分线交⊙O于点D,DE⊥AC
于E.
(1)求证:DE是⊙O的切线;
(2)若AB=10,AC=6,求ED的长.
【解答】(1)证明:连接OD,
∵DE⊥AE,
∴∠AED=90°,
∵AD平分∠BAE,
∴∠CAD=∠DAB,
∵OA=OD,
∴∠ADO=∠DAB,
∴∠CAD=∠ADO,
∴AC∥DO,
∴∠EDO=180°﹣∠E=90°,
∵OD是⊙O的半径,
∴DE是⊙O的切线;
(2)解:连接BC,
∵AB是⊙O的直径,
∴∠ACB=90°,
∴∠ECB=180°﹣∠ACB=90°,
∵∠E=∠EDO=90°,
∴四边形ECFD是矩形,
∴DE=CF,∠CFD=90°,
∵AB=10,AC=6,
∴BC8,
∵OD⊥BC,
∴CFBC=4,
∴DE=CF=4,
∴ED的长为4.
20.(2023秋 北京期末)在平面直角坐标系xOy中,点M(﹣1,m),N(3,n)在抛物线y=ax2+bx+c(a>0)上,设抛物线的对称轴为直线x=t.
(1)若m=n,求t的值;
(2)若c<m<n,求t的取值范围.
【解答】解:(1)由题意,若m=n,
∴对称轴是直线x1=t.
即t=1;
(2)∵抛物线y=ax2+bx+c的对称轴为直线x=t,
∴xt,
∴b=﹣2at,
∴y=ax2﹣2atx+c,
∵M(﹣1,m),N(3,n)在抛物线y=ax2+bx+c(a>0)上,
∴,
①﹣②得,m﹣n=﹣8a+8at,
∵m<n,
∴m﹣n<0,
∴﹣8a+8at<0,
∵a>0,
∴t<1,
由①得,m﹣c=a+2at,
∵c<m,
∴m﹣c>0,
∴a+2at>0,
∵a>0,
∴t,
∴t的取值范围为t<1.
21.(2023秋 迎江区校级期末)如图, ABCD的三个顶点B,C,D都在⊙O上,边AD与⊙O相交于点E,边AB与⊙O相切.
(1)求证:∠ABE=∠BCE;
(2)若CD=4,CE=5,求AE的长.
【解答】(1)证明:连接BO并延长,交⊙O于点F,连接EF.
∵BF是直径,
∴∠BEF=90°,
∴∠F+∠EBF=90°;
∵AB与⊙O相切于点B,
∴BF⊥AB,
∴∠EBF+∠ABE=90°,
∴∠F=∠ABE,
∵∠F=∠BCE,
∴∠ABE=∠BCE;
(2)解:∵四边形ABCD为平行四边形,
∴AB=CD=4,∠A=∠DCB,
∵∠AEB=∠DCB,
∴∠A=∠AEB,
∴BE=AB=4;
∵AD∥BC,
∴∠AEB=∠EBC,
∵∠ABE=∠BCE,
∴△ABE∽△ECB,
∴,
∴,
∴5AE=16,
∴AE.
22.(2023秋 奇台县校级期末)为助力脱贫攻坚,某村在“农村淘宝网店”上销售该村优质农产品,该网店于今年一月底收购一批每袋进价25元的农产品,售价为每袋40元,二月份销售192袋,三、四月该商品十分畅销,销售量持续走高,在售价不变的基础上,四月份的销售量达到300袋.
(1)求三、四这两个月销售量的月平均增长率;
(2)该网店五月降价促销,经调查发现,若该农产品每袋降价1元,销售量可增加5袋,当农产品每袋降价多少元时,这种农产品在五月份可获利3250元?
【解答】解:(1)设三、四这两个月的月平均增长率为x.
由题意得:192(1+x)2=300,
解得:(不合题意,舍去),
答:三、四这两个月的月平均增长率为25%;
(2)设当农产品每袋降价m元时,该淘宝网店五月份获利3250元.
根据题意可得:(40﹣25﹣m)(300+5m)=3250,
解得:m1=5,m2=﹣50(不合题意,舍去).
答:当农产品每袋降价5元时,该淘宝网店五月份获利3250元.
23.(2023秋 雁塔区校级期末)某校在元旦活动时布置教室,如图1,教室两墙AB、CD之间悬挂一条近似抛物线y=ax2﹣x+3的彩带,如图2,已知AB=CD,BD=6米.
(1)如图2,两墙AB、CD的高度是 3 米,抛物线的顶点坐标为 ;
(2)如图3,为了避免彩带太低影响人员走动且考虑美观,现把彩带从点M、N处用细线吊在天花板上,形成抛物线F1,F2,F3;点M到墙AB距离为2.5米,抛物线F1的最低点距墙AB的距离为2米且离地面2米,求点M到地面的距离.
【解答】解:(1)∵AB=CD,BD=6,
∴D(6,0),对称轴为直线x=3,
∴,
解得:,
∴,
当x=6时,
=3,
∴AB=CD=3(米),
当x=3时,
,
∴顶点坐标为,
故答案为:3,;
(2)解:∵点M到墙AB距离为2.5米,
∴xM=2.5,
∵抛物线F1的最低点距墙AB的距离为2米且离地面2米,
∴抛物线F1的顶点为(2,2),
∴可设抛物线F1的解析式为:y=m(x﹣2)2+2,
由(2)得:A(0,3),
∴m(0﹣2)2+2=3,
解得:,
∴抛物线F1的解析式为:,
当xM=2.5时,
,
答:点M到地面的距离为米.
24.(2023秋 呼兰区校级期末)如图1,在平面直角坐标系中,O为坐标原点,抛物线y=x2+bx+c与x轴负半轴交于点B,与x轴正半轴于点A(3,0),交y轴于点C,连接AC,tan∠OAC=1.
(1)求抛物线的解析式;
(2)如图2,点P为第三象限抛物线上一点,连接PB,PO,若设△POB的面积为S,点P的横坐标为t,求S与t的函数关系式(不要求写出自变量t的取值范围);
(3)在(2)的条件下,如图3,过点P作PE⊥x轴于点E,点K为抛物线的顶点,连接BK交PE于点F,点D为AK上一点,BF=DK,连接DF,若∠EBF﹣∠DFK=45°,求点P的坐标.
【解答】解:(1)∵抛物线y=﹣x2+bx+c与x轴正半轴于点A(3,0),
∴OA=3,
在Rt△AOC中,,
∴OC=OA=3,
∴C(0,﹣3),
把点A(3,0)、C(0,﹣3)代入y=x2+bx+c得:
,
解得:,
∴抛物线的解析式为y=x2﹣2x﹣3;
(2)当x2﹣2x﹣3=0时,
解得:x1=3,x2=﹣1,
∴B(﹣1,0),
∴OB=1,
∵点P在抛物线上,点P的横坐标为t,
∴P(t,t2﹣2t﹣3),
过点P作PL⊥x轴于点L,如图2,
∴PL=﹣t2+2t+3,
∴SOB PL1×(﹣t2+2t+3)t.
(3)∵y=x2﹣2x﹣3=(x﹣1)2﹣4,
∴K(1,4),
过点K作KM⊥AB于点M,交DF于点N,作FG⊥AK于点G,如图3,
根据对称性可知:BM=AM,BK=AK,∠BKM=∠AKM,
∵PE⊥AB,
∴PE∥KM,
∴∠BFE=∠BKM,
设∠BFE=∠BKM=α,
∴∠EBF=90°﹣α,
∵∠EBF﹣∠DFK=45°,
∴∠DFK=45°﹣α,
∴∠DFG=90°﹣∠DFK﹣∠FKM﹣∠AKM
=90°﹣(45°﹣α)﹣α﹣α
=45°﹣α,
∴∠DFK=∠DFG,
∴∠FNM=∠DFK+∠FKM=45﹣α+α=45°,
过点D作DH⊥KM,
∵BF=DK,∠DHK=∠BEF=90°,∠BFE=∠DKH,
∴△DHK≌△BEF(AAS),
∴DH=BE,HK=EF,
过点F作FT⊥KM于T,
∵∠DNH=∠FNT=45°,
∴△FTN与△HND都是等腰直角三角形,
∴DH=HN,FT=EM=TN,EF=MT=HK,
∵BM=2,MK=4,
∴,
∵点P的横坐标为t,
∴BE=DH=HN=1+t,
∴FE=MT=HK=2+2t,
∴EM=FT=TN=1﹣t,
∴MK=HK+HN+TN+MT=2+2t+1+t+1﹣t+2+2t=6+4t=4,
解得:,
,
∴.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
期末能力提升卷-2024-2025学年数学九年级上册人教版
一.选择题(共8小题)
1.(2023秋 四平期末)下列关于x的方程中,一定属于一元二次方程的是( )
A.ax2﹣2x+3=0 B.x2+9=0
C. D.x2+2y+6=0
2.(2023秋 南通期末)函数y=x2﹣4x+3图象顶点坐标是( )
A.(2,﹣1) B.(﹣2,1) C.(﹣2,﹣1) D.(2,1)
3.(2023秋 兖州区期末)剪纸艺术是最古老的中国民间艺术之一,先后入选中国国家级非物质文化遗产名录和人类非物质文化遗产代表作名录.以下剪纸中,为中心对称图形的是( )
A. B.
C. D.
4.(2023秋 宿迁期末)已知⊙O的半径为3,点P是直线l上的一点,OP=3,则直线l与⊙O的位置关系是( )
A.相离 B.相切
C.相交 D.相切或相交
5.(2022秋 宛城区校级期末)不透明的袋子中装有红、绿小球各一个,除颜色外两个小球无其他差别,从中随机摸出一个小球,放回并摇匀,再从中随机摸出一个小球,那么第一次摸到红球、第二次摸到绿球的概率是( )
A. B. C. D.
6.(2023秋 延长县校级期末)若关于x的一元二次方程(m﹣1)x2﹣mx+1=0有两个相等的实数根,则m的值是( )
A.﹣2 B.﹣1 C.1 D.2
7.(2023秋 交口县期末)如图,BC是⊙O的切线,点B是切点,连接CO交⊙O于点D,延长CO交⊙O于点A,连接AB,若∠C=30°,OD=2,则AB的长为( )
A. B. C. D.
8.(2023秋 荣昌区校级期末)如图,二次函数y=ax2+bx+c(a≠0)的图象经过点,对称轴为直线x=1,下列结论:①abc<0;②a﹣2b+4c=0;③2a+b>0;④a+b≤m(am+b)(其中m≠1);⑤b﹣c>0;正确的结论有( )
A.1个 B.3个 C.2个 D.4个
二.填空题(共8小题)
9.(2023秋 沈河区校级期末)关于x的一元二次方程x2+3x+k=0有一个根为x=2,则k的值为 .
10.(2023秋 东西湖区期末)在平面直角坐标系中,点(4,﹣5)关于原点的对称点的坐标是 .
11.(2023秋 大观区校级期末)如图,一下水管道横截面为圆形,直径为260cm,下雨前水面宽为100cm,一场大雨过后,水面宽为240cm,则水位上升 cm.
12.(2023秋 洛阳期末)如图,顺次连接等边三角形三边中点得到四个全等等边三角形.任意给其中两个涂色,涂色部分正好是菱形的概率是 .
13.(2023秋 绥中县期末)飞机着陆后滑行的距离S(m)关于滑行时间t(s)的函数解析式是S=﹣1.5t2+60t,飞机着陆后滑行 m才能停下来.
14.(2023秋 甘井子区校级期末)如图,已知⊙O的半径为2,AC与⊙O相切,连接AO并延长,交⊙O于点B,过点C作CD⊥AB,交⊙O于点D,连接BD,若∠A=30°,则弦BD的长为 .
15.(2023秋 连云港期末)如图,在平面直角坐标系中,正六边形OABCDE边长是6,则它的外接圆心P的坐标是 .
16.(2023秋 大观区校级期末)将抛物线y=﹣x2向右平移后,所得新抛物线的顶点是B,新抛物线与原抛物线交于点A(如图所示),连接OA、AB,如果△AOB是等边三角形,则OB的长为 .
三.解答题(共8小题)
17.(2023秋 琼海校级期末)解方程:
(1)x2﹣2x﹣2=0;
(2).
18.(2023秋 双阳区期末)杭州第19届亚运会吉祥物“江南忆”,具体指A.琮琮、B.宸宸、C.莲莲.如图是三张吉祥物的不透明卡片(卡片除内容外,其余均相同).将这三张卡片背面朝上洗匀放好,小李同学从这三张卡片中随机抽取一张后,再从剩余的两张卡片中随机抽取一张,请用树状图法或列表法,求两次抽到卡片恰好是琮琮和宸宸的概率.
19.(2023秋 定州市期末)如图,已知AB是⊙O的直径,AC是弦,∠BAC的角平分线交⊙O于点D,DE⊥AC
于E.
(1)求证:DE是⊙O的切线;
(2)若AB=10,AC=6,求ED的长.
20.(2023秋 北京期末)在平面直角坐标系xOy中,点M(﹣1,m),N(3,n)在抛物线y=ax2+bx+c(a>0)上,设抛物线的对称轴为直线x=t.
(1)若m=n,求t的值;
(2)若c<m<n,求t的取值范围.
21.(2023秋 迎江区校级期末)如图, ABCD的三个顶点B,C,D都在⊙O上,边AD与⊙O相交于点E,边AB与⊙O相切.
(1)求证:∠ABE=∠BCE;
(2)若CD=4,CE=5,求AE的长.
22.(2023秋 奇台县校级期末)为助力脱贫攻坚,某村在“农村淘宝网店”上销售该村优质农产品,该网店于今年一月底收购一批每袋进价25元的农产品,售价为每袋40元,二月份销售192袋,三、四月该商品十分畅销,销售量持续走高,在售价不变的基础上,四月份的销售量达到300袋.
(1)求三、四这两个月销售量的月平均增长率;
(2)该网店五月降价促销,经调查发现,若该农产品每袋降价1元,销售量可增加5袋,当农产品每袋降价多少元时,这种农产品在五月份可获利3250元?
23.(2023秋 雁塔区校级期末)某校在元旦活动时布置教室,如图1,教室两墙AB、CD之间悬挂一条近似抛物线y=ax2﹣x+3的彩带,如图2,已知AB=CD,BD=6米.
(1)如图2,两墙AB、CD的高度是 米,抛物线的顶点坐标为 ;
(2)如图3,为了避免彩带太低影响人员走动且考虑美观,现把彩带从点M、N处用细线吊在天花板上,形成抛物线F1,F2,F3;点M到墙AB距离为2.5米,抛物线F1的最低点距墙AB的距离为2米且离地面2米,求点M到地面的距离.
24.(2023秋 呼兰区校级期末)如图1,在平面直角坐标系中,O为坐标原点,抛物线y=x2+bx+c与x轴负半轴交于点B,与x轴正半轴于点A(3,0),交y轴于点C,连接AC,tan∠OAC=1.
(1)求抛物线的解析式;
(2)如图2,点P为第三象限抛物线上一点,连接PB,PO,若设△POB的面积为S,点P的横坐标为t,求S与t的函数关系式(不要求写出自变量t的取值范围);
(3)在(2)的条件下,如图3,过点P作PE⊥x轴于点E,点K为抛物线的顶点,连接BK交PE于点F,点D为AK上一点,BF=DK,连接DF,若∠EBF﹣∠DFK=45°,求点P的坐标.
期末能力提升卷-2024-2025学年数学九年级上册人教版
参考答案与试题解析
题号 1 2 3 4 5 6 7 8
答案 B A C D A D C A
一.选择题(共8小题)
1.(2023秋 四平期末)下列关于x的方程中,一定属于一元二次方程的是( )
A.ax2﹣2x+3=0 B.x2+9=0
C. D.x2+2y+6=0
【解答】A、ax2﹣2x+3=0,该方程的未知数的二次项系数是a,当a=0时不是一元二次方程,故本选项错误,不符合题意;
B、x2+9=0,该方程符合一元二次方程的定义,故本选项正确,符合题意;
C、该方程是分式方程,不是一元二次方程,故本选项错误,不符合题意;
D、x2+2y+6=0,该方程有两个未知数,该方程不是一元二次方程,故本选项错误,不符合题意.
故选:B.
2.(2023秋 南通期末)函数y=x2﹣4x+3图象顶点坐标是( )
A.(2,﹣1) B.(﹣2,1) C.(﹣2,﹣1) D.(2,1)
【解答】解:∵y=x2﹣4x+3,
=(x2﹣4x+4)﹣4+3,
=(x﹣2)2﹣1,
∴顶点坐标是(2,﹣1).
故选:A.
3.(2023秋 兖州区期末)剪纸艺术是最古老的中国民间艺术之一,先后入选中国国家级非物质文化遗产名录和人类非物质文化遗产代表作名录.以下剪纸中,为中心对称图形的是( )
A. B.
C. D.
【解答】解:A.该图形不是中心对称图形,故此选项不合题意;
B.该图形不是中心对称图形,故此选项不合题意;
C.该图形是中心对称图形,故此选项符合题意;
D.该图形不是中心对称图形,故此选项不合题意.
故选:C.
4.(2023秋 宿迁期末)已知⊙O的半径为3,点P是直线l上的一点,OP=3,则直线l与⊙O的位置关系是( )
A.相离 B.相切
C.相交 D.相切或相交
【解答】解:分为两种情况:①如图1,当OP⊥直线l时,此时直线l与⊙O的位置关系是相切;
②如图2,当OP和直线l不垂直时,此时直线l与⊙O相交;
所以直线l与⊙O的位置关系是相切或相交,
故选:D.
5.(2022秋 宛城区校级期末)不透明的袋子中装有红、绿小球各一个,除颜色外两个小球无其他差别,从中随机摸出一个小球,放回并摇匀,再从中随机摸出一个小球,那么第一次摸到红球、第二次摸到绿球的概率是( )
A. B. C. D.
【解答】解:列表如下:
红 绿
红 (红,红) (绿,红)
绿 (红,绿) (绿,绿)
所有等可能的情况有4种,其中第一次摸到红球、第二次摸到绿球的有1种情况,
所以第一次摸到红球、第二次摸到绿球的概率为,
故选:A.
6.(2023秋 延长县校级期末)若关于x的一元二次方程(m﹣1)x2﹣mx+1=0有两个相等的实数根,则m的值是( )
A.﹣2 B.﹣1 C.1 D.2
【解答】解:∵关于x的一元二次方程(m﹣1)x2﹣mx+1=0有两个相等的实数根,
∴Δ=b2﹣4ac=(﹣m)2﹣4×(m﹣1)=(m﹣2)2=0,且m﹣1≠0,
解得:m=2,
故选:D.
7.(2023秋 交口县期末)如图,BC是⊙O的切线,点B是切点,连接CO交⊙O于点D,延长CO交⊙O于点A,连接AB,若∠C=30°,OD=2,则AB的长为( )
A. B. C. D.
【解答】解:连接OB、DB,则OB=OD=2,
∵AD是⊙O的直径,
∴∠ABD=90°,AD=2OD=4,
∵BC与⊙O相切于点B,
∴BC⊥OB,
∴∠OBC=90°,
∵∠C=30°,
∴∠BOC=60°,
∴△BOD是等边三角形,
∴BD=OD=2,
∴AB2,
故选:C.
8.(2023秋 荣昌区校级期末)如图,二次函数y=ax2+bx+c(a≠0)的图象经过点,对称轴为直线x=1,下列结论:①abc<0;②a﹣2b+4c=0;③2a+b>0;④a+b≤m(am+b)(其中m≠1);⑤b﹣c>0;正确的结论有( )
A.1个 B.3个 C.2个 D.4个
【解答】解:①二次函数的图象开口向上,a>0,函数的对称轴在y轴右侧,则ab<0,而c<0,故abc>0,故①错误,不符合题意;
②将点代入函数表达式得:a﹣2b+4c=0,故②正确,符合题意;
③函数的对称轴为直线,即b=﹣2a,故2a+b=0,故③错误,不符合题意;
④当x=1时,函数取得最小值,又m≠1,则a+b+c<m(am+b)+c,即a+b<m(am+b),故④错误,不符合题意;
⑤由②③得:a﹣2b+4c=0,b=﹣2a,则,故,故⑤错误,不符合题意;
综上,②正确.
故选:A.
二.填空题(共8小题)
9.(2023秋 沈河区校级期末)关于x的一元二次方程x2+3x+k=0有一个根为x=2,则k的值为 ﹣10 .
【解答】解:∵x的一元二次方程x2+3x+k=0有一个根为x=2,
∴4+6+k=0,
解得k=﹣10.
故答案为:﹣10.
10.(2023秋 东西湖区期末)在平面直角坐标系中,点(4,﹣5)关于原点的对称点的坐标是 (﹣4,5) .
【解答】解:点(4,﹣5)关于原点的对称点的坐标是(﹣4,5),
故答案为:(﹣4,5).
11.(2023秋 大观区校级期末)如图,一下水管道横截面为圆形,直径为260cm,下雨前水面宽为100cm,一场大雨过后,水面宽为240cm,则水位上升 170或70 cm.
【解答】解:作半径OD⊥AB于C,连接OB,
由垂径定理得:BCAB=50cm,
在Rt△OBC中,OC120cm,
当水位上升到圆心以下,水面宽240cm时,
则OC′50cm,
水面上升的高度为:120﹣50=70cm;
当水位上升到圆心以上时,水面上升的高度为:120+50=170cm,
综上可得,水面上升的高度为170cm或70cm.
故答案为:170或70.
12.(2023秋 洛阳期末)如图,顺次连接等边三角形三边中点得到四个全等等边三角形.任意给其中两个涂色,涂色部分正好是菱形的概率是 .
【解答】解:∵任意给其中两个涂色,涂色部分正好是菱形的有3个,
∴涂色部分正好是菱形的概率是,
故答案为:.
13.(2023秋 绥中县期末)飞机着陆后滑行的距离S(m)关于滑行时间t(s)的函数解析式是S=﹣1.5t2+60t,飞机着陆后滑行 600 m才能停下来.
【解答】解:由题意,
S=﹣1.5t2+60t,
=﹣1.5(t2﹣40t+400﹣400)
=﹣1.5(t﹣20)2+600,
即当飞机着陆后滑行600m才能停下来时,飞机才能停下来.
故答案为:600.
14.(2023秋 甘井子区校级期末)如图,已知⊙O的半径为2,AC与⊙O相切,连接AO并延长,交⊙O于点B,过点C作CD⊥AB,交⊙O于点D,连接BD,若∠A=30°,则弦BD的长为 2 .
【解答】解:设AB交CD于E,交⊙O于F,连接OC、OD,如图,
∵AC与⊙O相切,
∴OC⊥AC,
∴∠OCA=90°,
∴∠AOC=90°﹣∠A=90°﹣30°=60°,
∵CD⊥AB,
∴,DE=CE,
∴∠DOF=∠COF=60°,
∴∠B∠DOF=30°,
在Rt△OCE中,∵OEOC=1,
∴CEOE,
∴DE,
在Rt△BDE中,BD=2DE=2.
故答案为:2.
15.(2023秋 连云港期末)如图,在平面直角坐标系中,正六边形OABCDE边长是6,则它的外接圆心P的坐标是 (3,3) .
【解答】解:连接PA,PO,
∵正六边形OABCDE的外接圆心是P,
∴∠OPA60°,PO=PA,
∴△POA是等边三角形,
∴PO=PA=OA=6,
过P作PH⊥OA于H,则∠OPH∠OPA=30°,OHOA=3,
∴PH3,
∴P的坐标是(3,3),
故答案为:(3,3).
16.(2023秋 大观区校级期末)将抛物线y=﹣x2向右平移后,所得新抛物线的顶点是B,新抛物线与原抛物线交于点A(如图所示),连接OA、AB,如果△AOB是等边三角形,则OB的长为 2 .
【解答】解:过A作AC⊥x轴于点C,
∵点A在抛物线y=﹣x2上,
∴设A(m,﹣m2),
∵△AOB是等边三角形,
∴BC=OC=m,,
∴或m=0(舍去),
∴,
故答案为:.
三.解答题(共8小题)
17.(2023秋 琼海校级期末)解方程:
(1)x2﹣2x﹣2=0;
(2).
【解答】解:(1)x2﹣2x﹣2=0,
移项得x2﹣2x=2,
配方得x2﹣2x+1=2+1,即(x+1)2=3,
开方得,
解得;;
(2),
去分母,得
m﹣4+m+2=0,
解得m=1,
经检验,m=1是原方程的根.
18.(2023秋 双阳区期末)杭州第19届亚运会吉祥物“江南忆”,具体指A.琮琮、B.宸宸、C.莲莲.如图是三张吉祥物的不透明卡片(卡片除内容外,其余均相同).将这三张卡片背面朝上洗匀放好,小李同学从这三张卡片中随机抽取一张后,再从剩余的两张卡片中随机抽取一张,请用树状图法或列表法,求两次抽到卡片恰好是琮琮和宸宸的概率.
【解答】解:画树状图如下:
共有6种等可能的结果,其中两次抽到卡片恰好是琮琮和宸宸有2种结果,
所以两次抽取的卡片上都是莲莲的概率为.
19.(2023秋 定州市期末)如图,已知AB是⊙O的直径,AC是弦,∠BAC的角平分线交⊙O于点D,DE⊥AC
于E.
(1)求证:DE是⊙O的切线;
(2)若AB=10,AC=6,求ED的长.
【解答】(1)证明:连接OD,
∵DE⊥AE,
∴∠AED=90°,
∵AD平分∠BAE,
∴∠CAD=∠DAB,
∵OA=OD,
∴∠ADO=∠DAB,
∴∠CAD=∠ADO,
∴AC∥DO,
∴∠EDO=180°﹣∠E=90°,
∵OD是⊙O的半径,
∴DE是⊙O的切线;
(2)解:连接BC,
∵AB是⊙O的直径,
∴∠ACB=90°,
∴∠ECB=180°﹣∠ACB=90°,
∵∠E=∠EDO=90°,
∴四边形ECFD是矩形,
∴DE=CF,∠CFD=90°,
∵AB=10,AC=6,
∴BC8,
∵OD⊥BC,
∴CFBC=4,
∴DE=CF=4,
∴ED的长为4.
20.(2023秋 北京期末)在平面直角坐标系xOy中,点M(﹣1,m),N(3,n)在抛物线y=ax2+bx+c(a>0)上,设抛物线的对称轴为直线x=t.
(1)若m=n,求t的值;
(2)若c<m<n,求t的取值范围.
【解答】解:(1)由题意,若m=n,
∴对称轴是直线x1=t.
即t=1;
(2)∵抛物线y=ax2+bx+c的对称轴为直线x=t,
∴xt,
∴b=﹣2at,
∴y=ax2﹣2atx+c,
∵M(﹣1,m),N(3,n)在抛物线y=ax2+bx+c(a>0)上,
∴,
①﹣②得,m﹣n=﹣8a+8at,
∵m<n,
∴m﹣n<0,
∴﹣8a+8at<0,
∵a>0,
∴t<1,
由①得,m﹣c=a+2at,
∵c<m,
∴m﹣c>0,
∴a+2at>0,
∵a>0,
∴t,
∴t的取值范围为t<1.
21.(2023秋 迎江区校级期末)如图, ABCD的三个顶点B,C,D都在⊙O上,边AD与⊙O相交于点E,边AB与⊙O相切.
(1)求证:∠ABE=∠BCE;
(2)若CD=4,CE=5,求AE的长.
【解答】(1)证明:连接BO并延长,交⊙O于点F,连接EF.
∵BF是直径,
∴∠BEF=90°,
∴∠F+∠EBF=90°;
∵AB与⊙O相切于点B,
∴BF⊥AB,
∴∠EBF+∠ABE=90°,
∴∠F=∠ABE,
∵∠F=∠BCE,
∴∠ABE=∠BCE;
(2)解:∵四边形ABCD为平行四边形,
∴AB=CD=4,∠A=∠DCB,
∵∠AEB=∠DCB,
∴∠A=∠AEB,
∴BE=AB=4;
∵AD∥BC,
∴∠AEB=∠EBC,
∵∠ABE=∠BCE,
∴△ABE∽△ECB,
∴,
∴,
∴5AE=16,
∴AE.
22.(2023秋 奇台县校级期末)为助力脱贫攻坚,某村在“农村淘宝网店”上销售该村优质农产品,该网店于今年一月底收购一批每袋进价25元的农产品,售价为每袋40元,二月份销售192袋,三、四月该商品十分畅销,销售量持续走高,在售价不变的基础上,四月份的销售量达到300袋.
(1)求三、四这两个月销售量的月平均增长率;
(2)该网店五月降价促销,经调查发现,若该农产品每袋降价1元,销售量可增加5袋,当农产品每袋降价多少元时,这种农产品在五月份可获利3250元?
【解答】解:(1)设三、四这两个月的月平均增长率为x.
由题意得:192(1+x)2=300,
解得:(不合题意,舍去),
答:三、四这两个月的月平均增长率为25%;
(2)设当农产品每袋降价m元时,该淘宝网店五月份获利3250元.
根据题意可得:(40﹣25﹣m)(300+5m)=3250,
解得:m1=5,m2=﹣50(不合题意,舍去).
答:当农产品每袋降价5元时,该淘宝网店五月份获利3250元.
23.(2023秋 雁塔区校级期末)某校在元旦活动时布置教室,如图1,教室两墙AB、CD之间悬挂一条近似抛物线y=ax2﹣x+3的彩带,如图2,已知AB=CD,BD=6米.
(1)如图2,两墙AB、CD的高度是 3 米,抛物线的顶点坐标为 ;
(2)如图3,为了避免彩带太低影响人员走动且考虑美观,现把彩带从点M、N处用细线吊在天花板上,形成抛物线F1,F2,F3;点M到墙AB距离为2.5米,抛物线F1的最低点距墙AB的距离为2米且离地面2米,求点M到地面的距离.
【解答】解:(1)∵AB=CD,BD=6,
∴D(6,0),对称轴为直线x=3,
∴,
解得:,
∴,
当x=6时,
=3,
∴AB=CD=3(米),
当x=3时,
,
∴顶点坐标为,
故答案为:3,;
(2)解:∵点M到墙AB距离为2.5米,
∴xM=2.5,
∵抛物线F1的最低点距墙AB的距离为2米且离地面2米,
∴抛物线F1的顶点为(2,2),
∴可设抛物线F1的解析式为:y=m(x﹣2)2+2,
由(2)得:A(0,3),
∴m(0﹣2)2+2=3,
解得:,
∴抛物线F1的解析式为:,
当xM=2.5时,
,
答:点M到地面的距离为米.
24.(2023秋 呼兰区校级期末)如图1,在平面直角坐标系中,O为坐标原点,抛物线y=x2+bx+c与x轴负半轴交于点B,与x轴正半轴于点A(3,0),交y轴于点C,连接AC,tan∠OAC=1.
(1)求抛物线的解析式;
(2)如图2,点P为第三象限抛物线上一点,连接PB,PO,若设△POB的面积为S,点P的横坐标为t,求S与t的函数关系式(不要求写出自变量t的取值范围);
(3)在(2)的条件下,如图3,过点P作PE⊥x轴于点E,点K为抛物线的顶点,连接BK交PE于点F,点D为AK上一点,BF=DK,连接DF,若∠EBF﹣∠DFK=45°,求点P的坐标.
【解答】解:(1)∵抛物线y=﹣x2+bx+c与x轴正半轴于点A(3,0),
∴OA=3,
在Rt△AOC中,,
∴OC=OA=3,
∴C(0,﹣3),
把点A(3,0)、C(0,﹣3)代入y=x2+bx+c得:
,
解得:,
∴抛物线的解析式为y=x2﹣2x﹣3;
(2)当x2﹣2x﹣3=0时,
解得:x1=3,x2=﹣1,
∴B(﹣1,0),
∴OB=1,
∵点P在抛物线上,点P的横坐标为t,
∴P(t,t2﹣2t﹣3),
过点P作PL⊥x轴于点L,如图2,
∴PL=﹣t2+2t+3,
∴SOB PL1×(﹣t2+2t+3)t.
(3)∵y=x2﹣2x﹣3=(x﹣1)2﹣4,
∴K(1,4),
过点K作KM⊥AB于点M,交DF于点N,作FG⊥AK于点G,如图3,
根据对称性可知:BM=AM,BK=AK,∠BKM=∠AKM,
∵PE⊥AB,
∴PE∥KM,
∴∠BFE=∠BKM,
设∠BFE=∠BKM=α,
∴∠EBF=90°﹣α,
∵∠EBF﹣∠DFK=45°,
∴∠DFK=45°﹣α,
∴∠DFG=90°﹣∠DFK﹣∠FKM﹣∠AKM
=90°﹣(45°﹣α)﹣α﹣α
=45°﹣α,
∴∠DFK=∠DFG,
∴∠FNM=∠DFK+∠FKM=45﹣α+α=45°,
过点D作DH⊥KM,
∵BF=DK,∠DHK=∠BEF=90°,∠BFE=∠DKH,
∴△DHK≌△BEF(AAS),
∴DH=BE,HK=EF,
过点F作FT⊥KM于T,
∵∠DNH=∠FNT=45°,
∴△FTN与△HND都是等腰直角三角形,
∴DH=HN,FT=EM=TN,EF=MT=HK,
∵BM=2,MK=4,
∴,
∵点P的横坐标为t,
∴BE=DH=HN=1+t,
∴FE=MT=HK=2+2t,
∴EM=FT=TN=1﹣t,
∴MK=HK+HN+TN+MT=2+2t+1+t+1﹣t+2+2t=6+4t=4,
解得:,
,
∴.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
