期末模拟测试卷(含解析)-2024-2025学年数学九年级上册苏科版
文档属性
| 名称 | 期末模拟测试卷(含解析)-2024-2025学年数学九年级上册苏科版 |

|
|
| 格式 | docx | ||
| 文件大小 | 1.9MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-01-23 00:00:00 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
期末模拟测试卷-2024-2025学年数学九年级上册苏科版
一、单选题
1.下列方程中,属于一元二次方程的是( )
A. B. C. D.
2.在寒假到来之际,王强计划从平遥古城、皇城相府、壶口瀑布、雁门关四个旅游景点中任意选择一个去游玩.如图,他将这四个旅游景点的图片制作成四张卡片(除内容外,其余完全相同).并将这四张卡片背面朝上,洗匀后随机抽取一张,恰好抽到平遥古城的概率为( )
A. B. C. D.
3.已知和是方程的两个解,则的值为( )
A.2020 B.2024 C.2026 D.2028
4.如图为直径,,则为( )
A. B. C. D.
5.一元二次方程的实数根的情况是( )
A.有两个不相等的实数根 B.有两个相等的实数根
C.没有实数根 D.无法判断
6.如图,正六边形内接于,已知的周长是,则该正六边形的边长是( )
A.3 B. C.6 D.
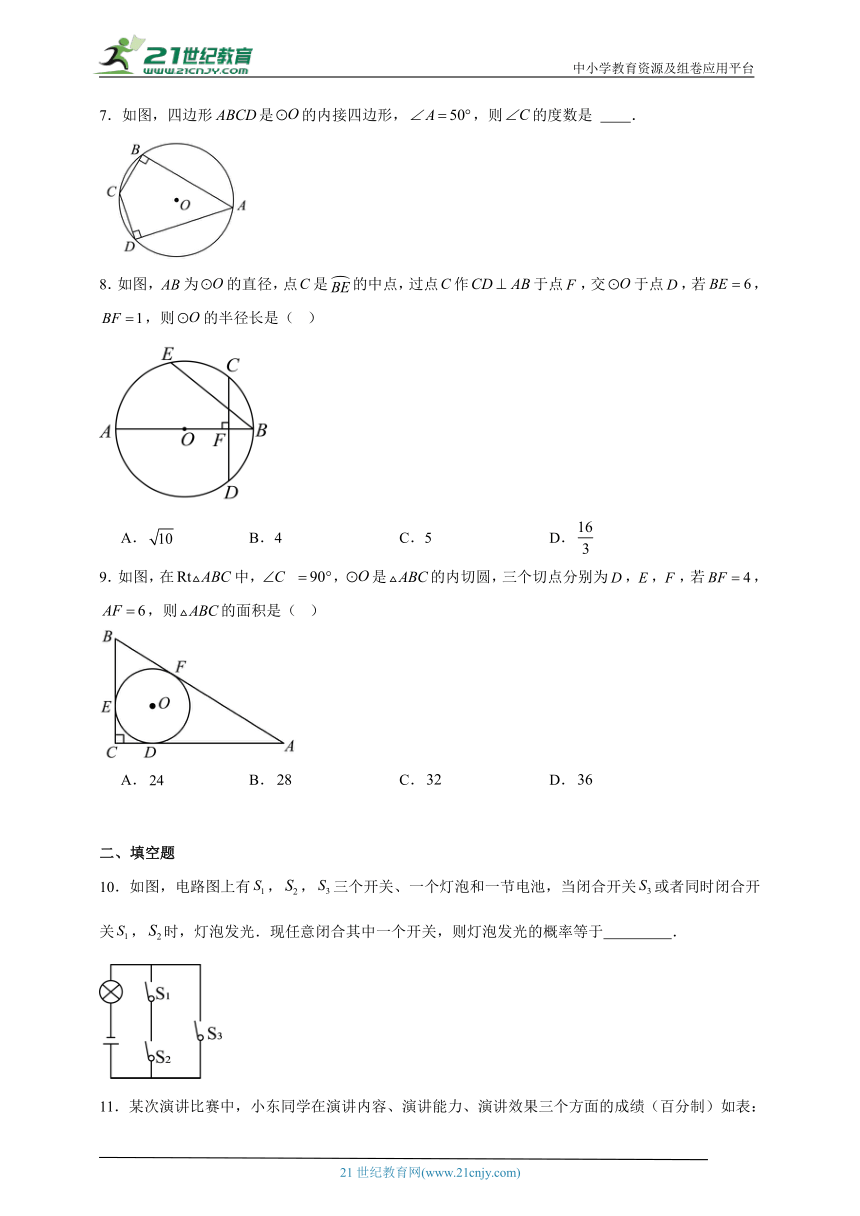
7.如图,四边形是的内接四边形,,则的度数是 .
8.如图,为的直径,点是的中点,过点作于点,交于点,若,,则的半径长是( )
A. B.4 C.5 D.
9.如图,在中, ,是的内切圆,三个切点分别为,,,若,,则的面积是( )
A. B. C. D.
二、填空题
10.如图,电路图上有,,三个开关、一个灯泡和一节电池,当闭合开关或者同时闭合开关,时,灯泡发光.现任意闭合其中一个开关,则灯泡发光的概率等于 .
11.某次演讲比赛中,小东同学在演讲内容、演讲能力、演讲效果三个方面的成绩(百分制)如表:若对演讲内容、演讲能力、演讲效果分别赋权5、3、2,则小东同学此次演讲比赛的平均成绩(百分制)是 .
演讲内容 演讲能力 演讲效果
分数 90 80 85
12.若是方程的一个实数根,则的值为 .
13.若a使得关于x的分式方程有整数解,且使得关于y的一元二次方程有实数根,则所有满足条件的整数a的和为 .
14.如图,扇形的圆心角为,点在圆弧上,,,阴影部分的面积为 .
15.如图,的半径弦于点,连接并延长交于点,连接.若,,则的长为 .
16.新能源汽车已逐渐成为人们喜爱的交通工具,据某品牌新能源汽车经销商8月份至10月份统计,该品牌新能源汽车8月份销售1000辆,10月份销售1690辆.设月平均增长率为,根据题意可列方程为 .
17.某游乐园的摩天轮(如图1)有均匀分布在圆形转轮边缘的若干个座舱,人们坐在座舱中可以俯瞰美景,图2是摩天轮的示意图.摩天轮以固定的速度绕中心O顺时针方向转动,转一圈为18分钟.从小刚由登舱点P进入摩天轮开始计时,到第6分钟时,他乘坐的座舱到达图2中的点 处(填A,B,C或D),此点距地面的高度为 .
三、解答题
18.解方程:.
19.先化简,再求值: ,其中x是方程的解.
20.又是一年脐橙丰收季!小石通过网络平台进行直播销售.已知每箱(小箱)脐橙的成本是元如果销售单价定为每箱元,那么日销售量将达到箱.据市场调查,销售单价每提高元,日销售量将减少箱.
(1)若销售单价定为每箱元(),请用含的式子表示日销售量;
(2)要使每天销售这种脐橙盈利元,同时又要让利给顾客,那么脐橙的售价单价应定为每箱多少元?
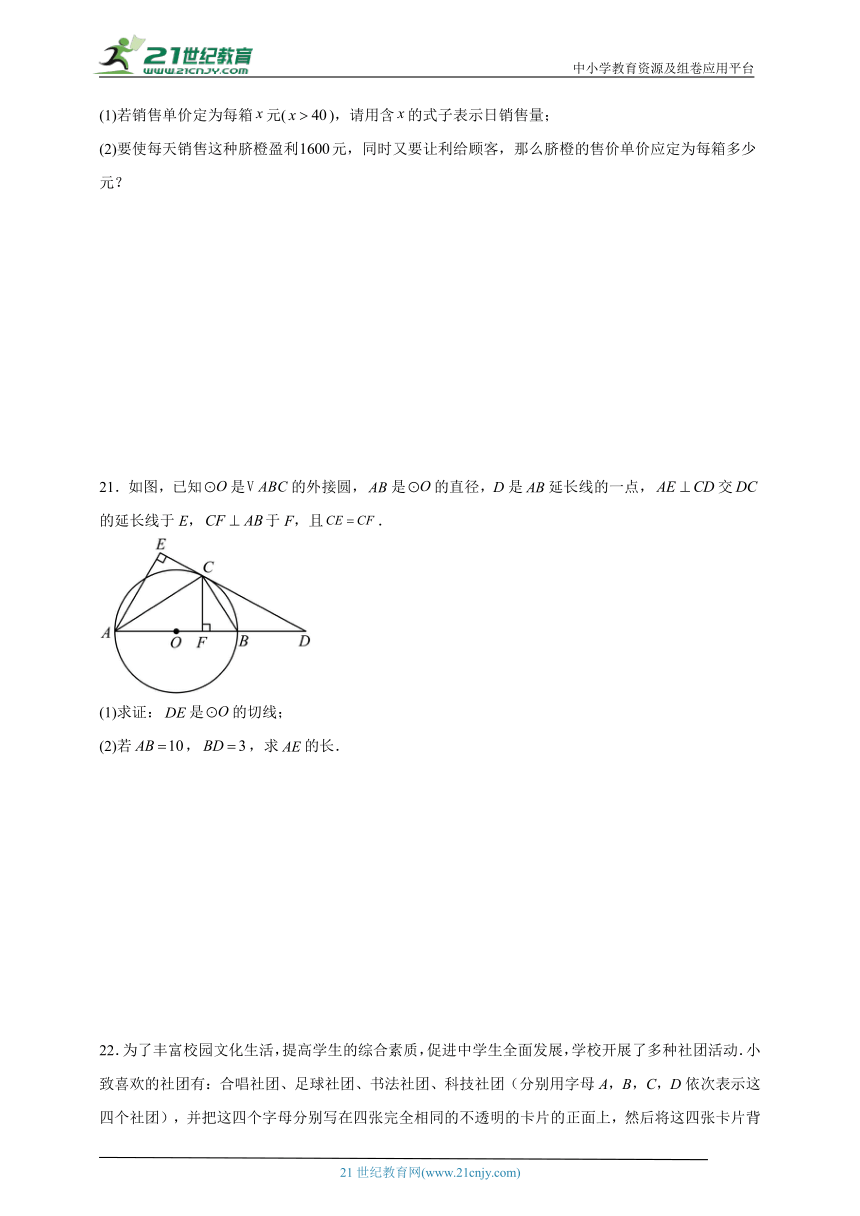
21.如图,已知是的外接圆,是的直径,D是延长线的一点,交的延长线于E,于F,且.
(1)求证:是的切线;
(2)若,,求的长.
22.为了丰富校园文化生活,提高学生的综合素质,促进中学生全面发展,学校开展了多种社团活动.小致喜欢的社团有:合唱社团、足球社团、书法社团、科技社团(分别用字母A,B,C,D依次表示这四个社团),并把这四个字母分别写在四张完全相同的不透明的卡片的正面上,然后将这四张卡片背面朝上洗匀后放在桌面上.
(1)小致从中随机抽取一张卡片是足球社团B的概率是______.
(2)小致先从中随机抽取一张卡片,记录下卡片上的字母后不放回,再从剩余的卡片中随机抽取一张卡片,记录下卡片上的字母,请你用列表法或画树状图法求出小致两次抽取的卡片中有一张是书法社团C的概率.
23.某超市于今年年初以每件元的进价购进一批商品.当商品售价为元时,一月份销售件.二、三月该商品十分畅销.销售量持续走高.在售价不变的基础上,三月底的销售量达到件.设二、三这两个月的月平均增长率不变.
(1)求二、三这两个月的月平均增长率;
(2)从四月份起,商场决定采用降价促销的方式回馈顾客,经调查发现,该商品每降价元,销售量增加件,当商品降价多少元时,商场获利元?
24.3月14日是国际数学日,“数学是打开科学大门的钥匙”.为进一步提高学生学习数学的兴趣,某校开展了一次数学趣味知识竞赛(竞赛成绩为百分制),并随机抽取了50名学生的竞赛成绩(本次竞赛没有满分),经过整理数据得到以下信息:
信息一:50名学生竞赛成绩频数分布直方图如图所示,从左到右依次为第一组到第五组(每组数据含前端点值,不含后端点值).
信息二:第三组成绩(单位:分)为74,71,73,74,79,76,77,76,76,73,72,75.
根据信息解答下列问题:
(1)补全频数分布直方图(直接在图中补全);
(2)第三组的成绩的众数是____________分,抽取的50名学生竞赛成绩的中位数是____________分;
(3)若该校共有名学生参赛,求该校参赛学生成绩不低于80分的约有多少人.
25.如图,是⊙O的直径,与相切于点B,连接、,过圆心O作,连接并延长,交延长线于点A.
(1)求证:;
(2)若F是的中点,的半径为2,求阴影部分的面积.
参考答案:
1.B
【分析】本题主要考查一元二次方程的定义,熟练掌握一元二次方程的定义是解题的关键;因此此题可根据“只含有一个未知数,且未知数的最高次数为2的整式方程”进行求解即可.
【详解】解:A、最高次数是1,故不是一元二次方程,故不符合题意;
B、是一元二次方程,故符合题意;
C、含分式,故不是一元二次方程,故不符合题意;
D、有两个未知量,故不是一元二次方程,故不符合题意;
故选B.
2.C
【分析】本题考查了简单的概率计算.熟练掌握简单的概率计算是解题的关键.
根据简单的概率计算公式求解作答即可.
【详解】解:由题意知,恰好抽到平遥古城的概率为,
故选:C.
3.D
【分析】本题考查一元二次方程的解和根与系数关系、代数式求值.先根据方程的解满足方程以及根与系数关系求得,,再代值求解即可.
【详解】解:∵a和b是方程的两个解,
∴,,
∴,
∴
,
故选:D.
4.C
【分析】本题考查了圆周角定理,根据,得出,再结合为直径,所以,即可作答.
【详解】解:∵,
∴,
∵为直径,
∴,
则,
故选:C
5.C
【分析】本题考查了根据判别式判断一元二次方程根的情况,熟练掌握一元二次方程根的判别式与根的情况之间的关系是解题的关键:当时,一元二次方程()有两个不相等的实数根;当时,一元二次方程()有两个相等的实数根;当时,一元二次方程()没有实数根.
先计算判别式得到,然后根据判别式判断方程根的情况即可.
【详解】解:将一元二次方程化为一般形式,得:
,
,
一元二次方程没有实数根,
故选:.
6.C
【分析】本题主要考查了圆内接正六边形的性质,等边三角形的判定及性质,正确运用圆与正六边形的性质是解此题的关键.
如图所示,由正六边形内接于,可知是等边三角形,由的周长是,可得,即可得出结果.
【详解】解:如图所示:连接,
∵正六边形内接于,
,
∵,
∴是等边三角形,
∵的周长是,
,
,
故选:C.
7./度
【分析】本题考查了圆内接四边形的性质,熟练掌握圆内接四边形的性质是解题的关键,根据圆内接四边形的对角互补计算即可.
【详解】解:∵四边形是的内接四边形,
∴,
∵,
∴,
故答案为:.
8.C
【分析】本题考查了垂径定理,弧、圆心角、弦之间的关系,勾股定理,熟练掌握知识点是解题的关键.
先根据垂径定理和点C是弧的中点得从,而得出,再利用勾股定理进行求解即可.
【详解】解:连接,如图,设的半径为r,
∵,为的直径,
,,
点是的中点,
,
,
,
解得:
的半径长是,
故选C.
9.A
【分析】本题主要考查三角形内切圆与切线长定理的应用,根据题意利用切线的性质以及正方形的判定方法得出四边形是正方形,进而利用勾股定理即可得出答案.
【详解】解:连接,,
是的内切圆,切点分别为,,,
,,,,
又,
四边形是矩形,
又,
矩形是正方形,设,则,
在中
,
解得:,
,,
.
故选:A.
10.
【分析】本题主要考查了用列举法求概率,根据概率公式计算概率等知识点,熟练掌握列举法的概念以及用列举法求概率的基本步骤是解题的关键:在一次试验中,如果可能出现的结果只有有限个,且各种结果出现的可能性大小相等,那么我们可通过列举试验结果的方法,分析出随机事件发生的概率,这种方法称为列举法;用列举法求概率的基本步骤如下:列举出一次试验的所有可能结果,假设共种;数出满足要求的结果数,假设共种;根据概率公式计算概率:概率.
按照用列举法求概率的基本步骤求解即可.
【详解】解:现任意闭合其中一个开关,则一次试验的所有可能结果共有种,即:
闭合,闭合,闭合,
满足要求的结果数共有种,即:
闭合,
(灯泡发光的概率),
故答案为:.
11.86
【分析】本题考查加权平均数的计算,掌握加权平均数的计算方法是解题的关键.利用加权平均数的计算方法解题即可.
【详解】解:(分)
∴小东同学此次演讲比赛的平均成绩(百分制)是86分.
故答案为:.
12.
【分析】本题考查了一元二次方程的解,代数式求值,解题的关键是注意“整体代入”数学思想的应用.
把代入已知方程可以求得,然后将其整体代入所求的代数式进行求值.
【详解】解:∵是方程的一个实数根,
∴
∴,
∴
∴.
故答案是:.
13.
【分析】本题考查了解分式方程、一元二次方程根的判别式,先解分式方程得出,结合题意得出或或或或或或,根据一元二次方程根的判别式求出且,从而得出或或,求和即可.
【详解】解:解方程得:,
∵a使得关于x的分式方程有整数解,且,
∴或或或或或或,
∵关于y的一元二次方程有实数根,
∴,,
解得:且,
∴或或,
∴所有满足条件的整数a的和为,
故答案为:.
14.
【分析】本题考查了扇形面积的计算,圆周角定理,等边三角形的性质和判定,通过平行线将阴影部分的面积转化为扇形的面积,熟练掌握扇形面积的计算公式是解题的关键.
【详解】解:连接,
,
,
又,
是等边三角形,
,
又,
,
,
,
,
故答案为:.
15.
【分析】根据垂径定理得出,设为x,则,根据勾股定理得出方程,求出x的值,连接,求出且,求出,根据勾股定理求出即可.
【详解】解:∵在中,,
∴,
∵,
∴,
设,则,
∵,
∴,
在中,
∴,
解得,
∴;
连接,
∵,
∴且,
∴,
∵,
∴,
在中,,
∴,
∴.
故答案为:.
【点睛】本题考查了勾股定理,垂径定理,三角形中位线的应用,用了方程思想,解题的关键是熟练掌握相关的定理和性质.
16.
【分析】本题主要考查一元二次方程的应用,设月平均增长率为,根据题意列出方程即可.
【详解】解:设月平均增长率为,根据题意可列方程为
故答案为:.
17. B 78
【分析】本题考查了圆的半径相等,勾股定理,旋转的性质,连接,由图2知,,而,故到第6分钟时,他乘坐的座舱到达图2中的点B处,过B作于F,过O作于E,则四边形是矩形,于是得到,,再由,得到,最后根据底座到底面的高度可得点C距地面的高度为.
【详解】解:连接,
由图2知,,而,故到第6分钟时,他乘坐的座舱到达图2中的点B处,
过B作于F,过O作于E,
则四边形是矩形,
∴,,
∵,
∴,
∴,
∵底座到底面的高度,
∴点C距地面的高度为,
故答案为:B,78.
18.,.
【分析】本题考查利用因式分解法求一元二次方程的解.方程左边提取公因式化为积的形式,然后利用两数相乘积为0,两因式中至少有一个为0转化为两个一元一次方程来求解.
【详解】解:分解因式得:,即,
可得:或,
解得:,.
19.;
【分析】本题考查了分式的化简求值,解一元二次方程,熟练掌握分式的化简求值是解题的关键.先将括号内的分式通分,进行分式的加减运算,然后进行分式的除法运算,得到化简结果,再求一元二次方程的根,得到,最后将代入化简结果即得答案.
【详解】原式
,
x是方程的根,
,,
又时,分式没有意义,
,
原式.
20.(1)[]或)
(2)这种脐橙的售价单价应定为每箱元
【分析】本题考查一元二次方程的实际应用:
(1)根据销售单价每提高元,日销售量将减少箱,列出代数式即可;
(2)根据总利润等于单件利润乘以销量,列出一元二次方程进行求解即可.
【详解】(1)解:由题意,得:;
(2)解:设这种脐橙的售价单价定为每箱元,则每箱的销售利润为元,
日销售量为件,
根据题意得:,
整理得:,
解得:,,
又要让利给顾客,
.
答:这种脐橙的售价单价应定为每箱元.
21.(1)见详解
(2)
【分析】(1)连接,由角平分线的判定定理得出,由等边对等角得出,从而得出,推出,由平行线的性质得出,即可得证;
(2)由题意得出,,由等面积法求出,由勾股定理得出,从而得出,再证明即可得出答案.
【详解】(1)证明:连接;
,,且,
,
,
,
,
,
,
∴是的切线.
(2)解:∵,,,
,
,
.
,
,
,
,
.
在和中,,,
,
.
【点睛】本题考查了切线的判定、角平分线的判定、等腰三角形的性质、勾股定理、三角形全等的判定与性质以及平行线的判定与性质,熟练掌握以上知识点并灵活运用,添加适当的辅助线是解此题的关键.
22.(1)
(2)
【分析】本题考查了用概率公式求概率,列表法或树状图法求概率,正确通过列表法或树状图法展示所有等可能的结果求出,再从中选出符合事件或的结果数目,然后根据概率公式求出事件或的概率是解题关键.
(1)直接根据概率公式求解;
(2)利用列表法展示所有12种等可能性结果,再找出小致两次抽取的卡片中有一张是科技社团的结果数,然后根据概率公式求解.
【详解】(1)解:小致从中随机抽取一张卡片是足球社团的概率,
故答案为:;
(2)解:列表如下:
由表可知共有12种等可能结果,小致两次抽取的卡片中有一张是科技社团的结果数为6种,
所以小致两次抽取的卡片中有一张是科技社团的概率为.
答:小致两次抽取的卡片中有一张是书法社团C的概率.
23.(1)
(2)元
【分析】本题考查一元二次方程的实际应用,正确的列出方程,是解题的关键:
(1)设二、三这两个月的月平均增长率为,根据平均增长率的等量关系:,列出方程进行求解即可;
(2)设商品降价元,根据总利润等于单件利润乘以销量,列出方程进行求解即可.
【详解】(1)解:设二、三这两个月的月平均增长率为,
根据题意可得,,
解得,(不合题意,舍去),
答:二、三这两个月的月平均增长率为;
(2)解:设当商品降价元时,商品获利元,
根据题意可得,,
解得,(不合题意,舍去),
答:当商品降价元时,商场获利元.
24.(1)见解析
(2)76;78;
(3)人.
【分析】本题考查直方图,从统计图中获取数量及数量之间的关系是解决问题的关键,样本估计总体是统计中常用的方法.
(1)用抽取的总人数减去第一组、第三组、第四组与第五组的人数即可得第二组的人数,然后再补全频数分布直方图即可;
(2)根据众数和中位数的定义求解即可;
(3)样本估计总体,样本中不低于80分的占,进而估计名学生中不低于80分的人数.
【详解】(1)第二组人数为:(人)
补全统计图如下:
(2)第三组竞赛成绩中76分出现次数最多,出现了3次,故众数为76分;
50个数据中,最中间的两个数据分别是第25个和26个数据,对应的分数为:77分和79分,它们的平均数为:(分),故中位数为78(分);
故答案为:76;78;
(3)(人),
即该校参赛学生成绩不低于80分的约有人.
25.(1)见解析
(2)
【分析】(1)先根据圆周角定理和平行线的性质证得,再根据等腰三角形的性质证得,进而可得证;
(2)先根据直角三角形斜边中线性质和等边三角形的判定证明是等边三角形,则,则,利用含30度角的直角三角形的性质求得,,然后利用阴影部分的面积等于求解即可.
【详解】(1)证明:连接,
∵是⊙O的直径,
∴,
∵,
∴,
∴,
∵与相相切于点B,
∴,
∴,
∴,
∵,
∴,
∴;
(2)解:如图,连接,
∵,F是的中点,
∴,
∵,
∴,
∴是等边三角形,
∴,
∵,即,
∴,
∴,,
∴阴影部分的面积为:.
【点睛】本题考查了圆周角定理、切线的性质、扇形面积公式、平行线的性质、等腰三角形的性质、等边三角形的判定与性质、直角三角形的性质,熟练掌握相关知识的联系与运用是解题的关键.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
期末模拟测试卷-2024-2025学年数学九年级上册苏科版
一、单选题
1.下列方程中,属于一元二次方程的是( )
A. B. C. D.
2.在寒假到来之际,王强计划从平遥古城、皇城相府、壶口瀑布、雁门关四个旅游景点中任意选择一个去游玩.如图,他将这四个旅游景点的图片制作成四张卡片(除内容外,其余完全相同).并将这四张卡片背面朝上,洗匀后随机抽取一张,恰好抽到平遥古城的概率为( )
A. B. C. D.
3.已知和是方程的两个解,则的值为( )
A.2020 B.2024 C.2026 D.2028
4.如图为直径,,则为( )
A. B. C. D.
5.一元二次方程的实数根的情况是( )
A.有两个不相等的实数根 B.有两个相等的实数根
C.没有实数根 D.无法判断
6.如图,正六边形内接于,已知的周长是,则该正六边形的边长是( )
A.3 B. C.6 D.
7.如图,四边形是的内接四边形,,则的度数是 .
8.如图,为的直径,点是的中点,过点作于点,交于点,若,,则的半径长是( )
A. B.4 C.5 D.
9.如图,在中, ,是的内切圆,三个切点分别为,,,若,,则的面积是( )
A. B. C. D.
二、填空题
10.如图,电路图上有,,三个开关、一个灯泡和一节电池,当闭合开关或者同时闭合开关,时,灯泡发光.现任意闭合其中一个开关,则灯泡发光的概率等于 .
11.某次演讲比赛中,小东同学在演讲内容、演讲能力、演讲效果三个方面的成绩(百分制)如表:若对演讲内容、演讲能力、演讲效果分别赋权5、3、2,则小东同学此次演讲比赛的平均成绩(百分制)是 .
演讲内容 演讲能力 演讲效果
分数 90 80 85
12.若是方程的一个实数根,则的值为 .
13.若a使得关于x的分式方程有整数解,且使得关于y的一元二次方程有实数根,则所有满足条件的整数a的和为 .
14.如图,扇形的圆心角为,点在圆弧上,,,阴影部分的面积为 .
15.如图,的半径弦于点,连接并延长交于点,连接.若,,则的长为 .
16.新能源汽车已逐渐成为人们喜爱的交通工具,据某品牌新能源汽车经销商8月份至10月份统计,该品牌新能源汽车8月份销售1000辆,10月份销售1690辆.设月平均增长率为,根据题意可列方程为 .
17.某游乐园的摩天轮(如图1)有均匀分布在圆形转轮边缘的若干个座舱,人们坐在座舱中可以俯瞰美景,图2是摩天轮的示意图.摩天轮以固定的速度绕中心O顺时针方向转动,转一圈为18分钟.从小刚由登舱点P进入摩天轮开始计时,到第6分钟时,他乘坐的座舱到达图2中的点 处(填A,B,C或D),此点距地面的高度为 .
三、解答题
18.解方程:.
19.先化简,再求值: ,其中x是方程的解.
20.又是一年脐橙丰收季!小石通过网络平台进行直播销售.已知每箱(小箱)脐橙的成本是元如果销售单价定为每箱元,那么日销售量将达到箱.据市场调查,销售单价每提高元,日销售量将减少箱.
(1)若销售单价定为每箱元(),请用含的式子表示日销售量;
(2)要使每天销售这种脐橙盈利元,同时又要让利给顾客,那么脐橙的售价单价应定为每箱多少元?
21.如图,已知是的外接圆,是的直径,D是延长线的一点,交的延长线于E,于F,且.
(1)求证:是的切线;
(2)若,,求的长.
22.为了丰富校园文化生活,提高学生的综合素质,促进中学生全面发展,学校开展了多种社团活动.小致喜欢的社团有:合唱社团、足球社团、书法社团、科技社团(分别用字母A,B,C,D依次表示这四个社团),并把这四个字母分别写在四张完全相同的不透明的卡片的正面上,然后将这四张卡片背面朝上洗匀后放在桌面上.
(1)小致从中随机抽取一张卡片是足球社团B的概率是______.
(2)小致先从中随机抽取一张卡片,记录下卡片上的字母后不放回,再从剩余的卡片中随机抽取一张卡片,记录下卡片上的字母,请你用列表法或画树状图法求出小致两次抽取的卡片中有一张是书法社团C的概率.
23.某超市于今年年初以每件元的进价购进一批商品.当商品售价为元时,一月份销售件.二、三月该商品十分畅销.销售量持续走高.在售价不变的基础上,三月底的销售量达到件.设二、三这两个月的月平均增长率不变.
(1)求二、三这两个月的月平均增长率;
(2)从四月份起,商场决定采用降价促销的方式回馈顾客,经调查发现,该商品每降价元,销售量增加件,当商品降价多少元时,商场获利元?
24.3月14日是国际数学日,“数学是打开科学大门的钥匙”.为进一步提高学生学习数学的兴趣,某校开展了一次数学趣味知识竞赛(竞赛成绩为百分制),并随机抽取了50名学生的竞赛成绩(本次竞赛没有满分),经过整理数据得到以下信息:
信息一:50名学生竞赛成绩频数分布直方图如图所示,从左到右依次为第一组到第五组(每组数据含前端点值,不含后端点值).
信息二:第三组成绩(单位:分)为74,71,73,74,79,76,77,76,76,73,72,75.
根据信息解答下列问题:
(1)补全频数分布直方图(直接在图中补全);
(2)第三组的成绩的众数是____________分,抽取的50名学生竞赛成绩的中位数是____________分;
(3)若该校共有名学生参赛,求该校参赛学生成绩不低于80分的约有多少人.
25.如图,是⊙O的直径,与相切于点B,连接、,过圆心O作,连接并延长,交延长线于点A.
(1)求证:;
(2)若F是的中点,的半径为2,求阴影部分的面积.
参考答案:
1.B
【分析】本题主要考查一元二次方程的定义,熟练掌握一元二次方程的定义是解题的关键;因此此题可根据“只含有一个未知数,且未知数的最高次数为2的整式方程”进行求解即可.
【详解】解:A、最高次数是1,故不是一元二次方程,故不符合题意;
B、是一元二次方程,故符合题意;
C、含分式,故不是一元二次方程,故不符合题意;
D、有两个未知量,故不是一元二次方程,故不符合题意;
故选B.
2.C
【分析】本题考查了简单的概率计算.熟练掌握简单的概率计算是解题的关键.
根据简单的概率计算公式求解作答即可.
【详解】解:由题意知,恰好抽到平遥古城的概率为,
故选:C.
3.D
【分析】本题考查一元二次方程的解和根与系数关系、代数式求值.先根据方程的解满足方程以及根与系数关系求得,,再代值求解即可.
【详解】解:∵a和b是方程的两个解,
∴,,
∴,
∴
,
故选:D.
4.C
【分析】本题考查了圆周角定理,根据,得出,再结合为直径,所以,即可作答.
【详解】解:∵,
∴,
∵为直径,
∴,
则,
故选:C
5.C
【分析】本题考查了根据判别式判断一元二次方程根的情况,熟练掌握一元二次方程根的判别式与根的情况之间的关系是解题的关键:当时,一元二次方程()有两个不相等的实数根;当时,一元二次方程()有两个相等的实数根;当时,一元二次方程()没有实数根.
先计算判别式得到,然后根据判别式判断方程根的情况即可.
【详解】解:将一元二次方程化为一般形式,得:
,
,
一元二次方程没有实数根,
故选:.
6.C
【分析】本题主要考查了圆内接正六边形的性质,等边三角形的判定及性质,正确运用圆与正六边形的性质是解此题的关键.
如图所示,由正六边形内接于,可知是等边三角形,由的周长是,可得,即可得出结果.
【详解】解:如图所示:连接,
∵正六边形内接于,
,
∵,
∴是等边三角形,
∵的周长是,
,
,
故选:C.
7./度
【分析】本题考查了圆内接四边形的性质,熟练掌握圆内接四边形的性质是解题的关键,根据圆内接四边形的对角互补计算即可.
【详解】解:∵四边形是的内接四边形,
∴,
∵,
∴,
故答案为:.
8.C
【分析】本题考查了垂径定理,弧、圆心角、弦之间的关系,勾股定理,熟练掌握知识点是解题的关键.
先根据垂径定理和点C是弧的中点得从,而得出,再利用勾股定理进行求解即可.
【详解】解:连接,如图,设的半径为r,
∵,为的直径,
,,
点是的中点,
,
,
,
解得:
的半径长是,
故选C.
9.A
【分析】本题主要考查三角形内切圆与切线长定理的应用,根据题意利用切线的性质以及正方形的判定方法得出四边形是正方形,进而利用勾股定理即可得出答案.
【详解】解:连接,,
是的内切圆,切点分别为,,,
,,,,
又,
四边形是矩形,
又,
矩形是正方形,设,则,
在中
,
解得:,
,,
.
故选:A.
10.
【分析】本题主要考查了用列举法求概率,根据概率公式计算概率等知识点,熟练掌握列举法的概念以及用列举法求概率的基本步骤是解题的关键:在一次试验中,如果可能出现的结果只有有限个,且各种结果出现的可能性大小相等,那么我们可通过列举试验结果的方法,分析出随机事件发生的概率,这种方法称为列举法;用列举法求概率的基本步骤如下:列举出一次试验的所有可能结果,假设共种;数出满足要求的结果数,假设共种;根据概率公式计算概率:概率.
按照用列举法求概率的基本步骤求解即可.
【详解】解:现任意闭合其中一个开关,则一次试验的所有可能结果共有种,即:
闭合,闭合,闭合,
满足要求的结果数共有种,即:
闭合,
(灯泡发光的概率),
故答案为:.
11.86
【分析】本题考查加权平均数的计算,掌握加权平均数的计算方法是解题的关键.利用加权平均数的计算方法解题即可.
【详解】解:(分)
∴小东同学此次演讲比赛的平均成绩(百分制)是86分.
故答案为:.
12.
【分析】本题考查了一元二次方程的解,代数式求值,解题的关键是注意“整体代入”数学思想的应用.
把代入已知方程可以求得,然后将其整体代入所求的代数式进行求值.
【详解】解:∵是方程的一个实数根,
∴
∴,
∴
∴.
故答案是:.
13.
【分析】本题考查了解分式方程、一元二次方程根的判别式,先解分式方程得出,结合题意得出或或或或或或,根据一元二次方程根的判别式求出且,从而得出或或,求和即可.
【详解】解:解方程得:,
∵a使得关于x的分式方程有整数解,且,
∴或或或或或或,
∵关于y的一元二次方程有实数根,
∴,,
解得:且,
∴或或,
∴所有满足条件的整数a的和为,
故答案为:.
14.
【分析】本题考查了扇形面积的计算,圆周角定理,等边三角形的性质和判定,通过平行线将阴影部分的面积转化为扇形的面积,熟练掌握扇形面积的计算公式是解题的关键.
【详解】解:连接,
,
,
又,
是等边三角形,
,
又,
,
,
,
,
故答案为:.
15.
【分析】根据垂径定理得出,设为x,则,根据勾股定理得出方程,求出x的值,连接,求出且,求出,根据勾股定理求出即可.
【详解】解:∵在中,,
∴,
∵,
∴,
设,则,
∵,
∴,
在中,
∴,
解得,
∴;
连接,
∵,
∴且,
∴,
∵,
∴,
在中,,
∴,
∴.
故答案为:.
【点睛】本题考查了勾股定理,垂径定理,三角形中位线的应用,用了方程思想,解题的关键是熟练掌握相关的定理和性质.
16.
【分析】本题主要考查一元二次方程的应用,设月平均增长率为,根据题意列出方程即可.
【详解】解:设月平均增长率为,根据题意可列方程为
故答案为:.
17. B 78
【分析】本题考查了圆的半径相等,勾股定理,旋转的性质,连接,由图2知,,而,故到第6分钟时,他乘坐的座舱到达图2中的点B处,过B作于F,过O作于E,则四边形是矩形,于是得到,,再由,得到,最后根据底座到底面的高度可得点C距地面的高度为.
【详解】解:连接,
由图2知,,而,故到第6分钟时,他乘坐的座舱到达图2中的点B处,
过B作于F,过O作于E,
则四边形是矩形,
∴,,
∵,
∴,
∴,
∵底座到底面的高度,
∴点C距地面的高度为,
故答案为:B,78.
18.,.
【分析】本题考查利用因式分解法求一元二次方程的解.方程左边提取公因式化为积的形式,然后利用两数相乘积为0,两因式中至少有一个为0转化为两个一元一次方程来求解.
【详解】解:分解因式得:,即,
可得:或,
解得:,.
19.;
【分析】本题考查了分式的化简求值,解一元二次方程,熟练掌握分式的化简求值是解题的关键.先将括号内的分式通分,进行分式的加减运算,然后进行分式的除法运算,得到化简结果,再求一元二次方程的根,得到,最后将代入化简结果即得答案.
【详解】原式
,
x是方程的根,
,,
又时,分式没有意义,
,
原式.
20.(1)[]或)
(2)这种脐橙的售价单价应定为每箱元
【分析】本题考查一元二次方程的实际应用:
(1)根据销售单价每提高元,日销售量将减少箱,列出代数式即可;
(2)根据总利润等于单件利润乘以销量,列出一元二次方程进行求解即可.
【详解】(1)解:由题意,得:;
(2)解:设这种脐橙的售价单价定为每箱元,则每箱的销售利润为元,
日销售量为件,
根据题意得:,
整理得:,
解得:,,
又要让利给顾客,
.
答:这种脐橙的售价单价应定为每箱元.
21.(1)见详解
(2)
【分析】(1)连接,由角平分线的判定定理得出,由等边对等角得出,从而得出,推出,由平行线的性质得出,即可得证;
(2)由题意得出,,由等面积法求出,由勾股定理得出,从而得出,再证明即可得出答案.
【详解】(1)证明:连接;
,,且,
,
,
,
,
,
,
∴是的切线.
(2)解:∵,,,
,
,
.
,
,
,
,
.
在和中,,,
,
.
【点睛】本题考查了切线的判定、角平分线的判定、等腰三角形的性质、勾股定理、三角形全等的判定与性质以及平行线的判定与性质,熟练掌握以上知识点并灵活运用,添加适当的辅助线是解此题的关键.
22.(1)
(2)
【分析】本题考查了用概率公式求概率,列表法或树状图法求概率,正确通过列表法或树状图法展示所有等可能的结果求出,再从中选出符合事件或的结果数目,然后根据概率公式求出事件或的概率是解题关键.
(1)直接根据概率公式求解;
(2)利用列表法展示所有12种等可能性结果,再找出小致两次抽取的卡片中有一张是科技社团的结果数,然后根据概率公式求解.
【详解】(1)解:小致从中随机抽取一张卡片是足球社团的概率,
故答案为:;
(2)解:列表如下:
由表可知共有12种等可能结果,小致两次抽取的卡片中有一张是科技社团的结果数为6种,
所以小致两次抽取的卡片中有一张是科技社团的概率为.
答:小致两次抽取的卡片中有一张是书法社团C的概率.
23.(1)
(2)元
【分析】本题考查一元二次方程的实际应用,正确的列出方程,是解题的关键:
(1)设二、三这两个月的月平均增长率为,根据平均增长率的等量关系:,列出方程进行求解即可;
(2)设商品降价元,根据总利润等于单件利润乘以销量,列出方程进行求解即可.
【详解】(1)解:设二、三这两个月的月平均增长率为,
根据题意可得,,
解得,(不合题意,舍去),
答:二、三这两个月的月平均增长率为;
(2)解:设当商品降价元时,商品获利元,
根据题意可得,,
解得,(不合题意,舍去),
答:当商品降价元时,商场获利元.
24.(1)见解析
(2)76;78;
(3)人.
【分析】本题考查直方图,从统计图中获取数量及数量之间的关系是解决问题的关键,样本估计总体是统计中常用的方法.
(1)用抽取的总人数减去第一组、第三组、第四组与第五组的人数即可得第二组的人数,然后再补全频数分布直方图即可;
(2)根据众数和中位数的定义求解即可;
(3)样本估计总体,样本中不低于80分的占,进而估计名学生中不低于80分的人数.
【详解】(1)第二组人数为:(人)
补全统计图如下:
(2)第三组竞赛成绩中76分出现次数最多,出现了3次,故众数为76分;
50个数据中,最中间的两个数据分别是第25个和26个数据,对应的分数为:77分和79分,它们的平均数为:(分),故中位数为78(分);
故答案为:76;78;
(3)(人),
即该校参赛学生成绩不低于80分的约有人.
25.(1)见解析
(2)
【分析】(1)先根据圆周角定理和平行线的性质证得,再根据等腰三角形的性质证得,进而可得证;
(2)先根据直角三角形斜边中线性质和等边三角形的判定证明是等边三角形,则,则,利用含30度角的直角三角形的性质求得,,然后利用阴影部分的面积等于求解即可.
【详解】(1)证明:连接,
∵是⊙O的直径,
∴,
∵,
∴,
∴,
∵与相相切于点B,
∴,
∴,
∴,
∵,
∴,
∴;
(2)解:如图,连接,
∵,F是的中点,
∴,
∵,
∴,
∴是等边三角形,
∴,
∵,即,
∴,
∴,,
∴阴影部分的面积为:.
【点睛】本题考查了圆周角定理、切线的性质、扇形面积公式、平行线的性质、等腰三角形的性质、等边三角形的判定与性质、直角三角形的性质,熟练掌握相关知识的联系与运用是解题的关键.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
