1.4 数列在日常经济生活中的应用 课件(共17张PPT)2024-2025学年北师大版(2019)高中数学选择性必修第二册
文档属性
| 名称 | 1.4 数列在日常经济生活中的应用 课件(共17张PPT)2024-2025学年北师大版(2019)高中数学选择性必修第二册 |  | |
| 格式 | pptx | ||
| 文件大小 | 670.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-01-23 14:25:14 | ||
图片预览





文档简介
(共17张PPT)
1.4 数列在日常经济生活中的应用
北师大版(2019)选择性必修二
1.了解单利、复利的概念.
2.掌握零存整取模型、定期自动转存模型、分期付款模型等三种模型及应用.
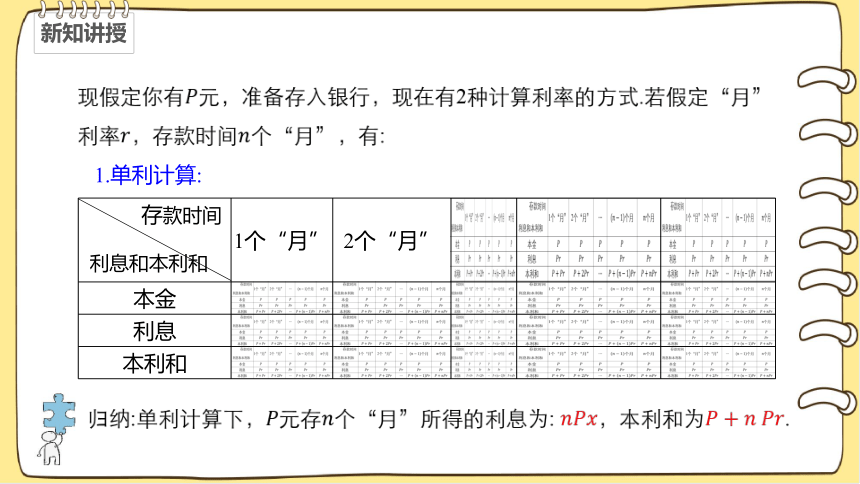
现假定你有元,准备存入银行,现在有2种计算利率的方式.若假定“月”利率,存款时间个“月”,有:
存款时间 利息和本利和 1个“月” 2个“月”
本金
利息
本利和
1.单利计算:
归纳:单利计算下,元存个“月”所得的利息为: ,本利和为.
存款时间 利息和本利和 1个“月” 2个“月”
本金
利息
本利和
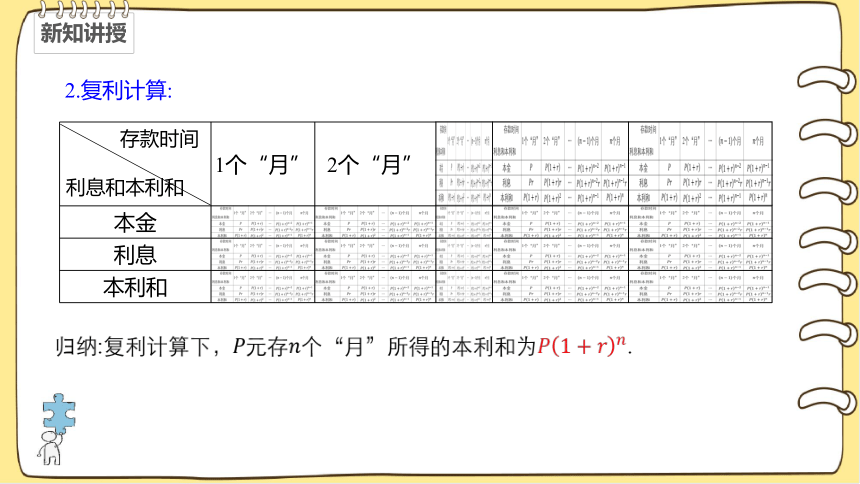
2.复利计算:
归纳:复利计算下,元存个“月”所得的本利和为.
思考:总结复利计算和单利计算的最大不同点.
单利计算中本金为定值,前一个月的利息不计入下一个本金,即本金所产生的利息不计算利息,满足关系:;
复利计算中,下一个计息周期内的本金为前一个周期的本金及其利息和,即以前各计息周期内产生的利息也计算利息,满足关系,即.
例1 李先生为今年上高中的儿子办理了“教育储蓄”,从8月1日开始,每个月的1日都存入100元,存期三年.
(1)已知当年“教育储蓄”存款的月利率是2.7‰.问时,李先生一次可支取本息多少元?
(2)已知当年同档次的“零存整取”储蓄的月利率是1.725‰.问李先生办理“教育储蓄”比“零存整取”多收益多少元?(注:零存整取要收20%的利息税)
解:(1)100×36+100×2.7‰×=3 779.82(元).
即“教育储蓄”一次支取本息3 779.82元.
(2)100×36+100×1.725‰××(1-20%)=3691.908≈3 691.91(元).
3 779.82-3 691.91=87.91(元)
∴比“零存整取”多收益87.91元.
零存整取问题在计算利息时,每次存入的钱不计复利,即对应等差数列模型.
归纳总结
例2 某家庭打算以一年定期的方式存款,计划从2018年起,每年年初到银行新存入a元,年利率p保持不变,并按复利计算,到2028年年初将所有存款和利息全部取出,一共可以取回多少钱?
解:设从2018年年初到2028年年初每年存入a元的本利和组成数列{an}(1≤n≤10).
则a1=a(1+p)10,a2=a(1+p)9,…,a10=a(1+p),
故数列{an}(1≤n≤10)是以a1=a(1+p)10为首项,q=为公比的等比数列.
所以2028年初这个家庭应取出的钱数为
S10==[(1+p)11-(1+p)](元).
复利问题可以转化为等比数列问题,第n年的本息=本金×(1+利率)n.
归纳总结
例3 小张老师年初向银行贷款2万元用于买车,银行贷款的年利率为10%,按复利计算.若这笔贷款要分10年等额还清,每年年初还一次,并且从借款后次年年初开始归还,问每年应还多少元?(精确到1元)
解:设每年还款x元,需10年还清,则每年还款及利息情况如下:
第10年还款x元,此次欠款全部还清;
第9年还款x元,过1年欠款全部还清时,所付款连同利息之和为x(1+10%)元;
第8年还款x元,过2年欠款全部还清时,所付款连同利息之和为x(1+10%)2元;
……
第1年还款x元,过9年欠款全部还清时,所付款连同利息之和为x(1+10%)9元.
根据题意可得:
x+x(1+10%)+x(1+10%)2+…+x(1+10%)9=20 000(1+10%)10,
∴x=≈3 255.
∴每年应还款3 255元.
分期付款的相关规定:
(1)分期付款中,每期的利息均按复利计算,分期付款中规定每期所付款额相同;
(2)各期所付款额连同到最后一次付款时所产生的利息之和等于商品售价及从购买到最后一次付款时的利息之和(此为列方程的依据);
(3)每期付款增值后的款数及售价增值后的款数均按S=P(1+r)n来计算,其中P代表本金(可以是每期付款额x,也可以是商品售价),n代表存期(月数或年数),r代表利率,S代表本利和.
归纳总结
1.在分期付款中,期数增多,其他条件不变,每次付款额( )
A.增多 B.减少
C.不变 D.可增多也可减少
2.现存入银行10 000元钱,年利率是3.60%,那么按照复利,第5年末的本利和是( )
A.10 000×1.0363 B.10 000×1.0364
C.10 000×1.0365 D.10 000×1.0366
B
C
3.某人在一年12个月中,每月10日向银行存入1 000元,假设银行的月利率为5‰(按单利计算),则到第二年的元月10日,此项存款一年的利息之和是( )
A.5(1+2+3+…+12)元
B.5(1+2+3+…+11)元
C.1 000[1+5‰+(5‰)2+…+(5‰)11]元
D.1 000[1+5‰+(5‰)2+…+(5‰)12]元
A
1.4 数列在日常经济生活中的应用
北师大版(2019)选择性必修二
1.了解单利、复利的概念.
2.掌握零存整取模型、定期自动转存模型、分期付款模型等三种模型及应用.
现假定你有元,准备存入银行,现在有2种计算利率的方式.若假定“月”利率,存款时间个“月”,有:
存款时间 利息和本利和 1个“月” 2个“月”
本金
利息
本利和
1.单利计算:
归纳:单利计算下,元存个“月”所得的利息为: ,本利和为.
存款时间 利息和本利和 1个“月” 2个“月”
本金
利息
本利和
2.复利计算:
归纳:复利计算下,元存个“月”所得的本利和为.
思考:总结复利计算和单利计算的最大不同点.
单利计算中本金为定值,前一个月的利息不计入下一个本金,即本金所产生的利息不计算利息,满足关系:;
复利计算中,下一个计息周期内的本金为前一个周期的本金及其利息和,即以前各计息周期内产生的利息也计算利息,满足关系,即.
例1 李先生为今年上高中的儿子办理了“教育储蓄”,从8月1日开始,每个月的1日都存入100元,存期三年.
(1)已知当年“教育储蓄”存款的月利率是2.7‰.问时,李先生一次可支取本息多少元?
(2)已知当年同档次的“零存整取”储蓄的月利率是1.725‰.问李先生办理“教育储蓄”比“零存整取”多收益多少元?(注:零存整取要收20%的利息税)
解:(1)100×36+100×2.7‰×=3 779.82(元).
即“教育储蓄”一次支取本息3 779.82元.
(2)100×36+100×1.725‰××(1-20%)=3691.908≈3 691.91(元).
3 779.82-3 691.91=87.91(元)
∴比“零存整取”多收益87.91元.
零存整取问题在计算利息时,每次存入的钱不计复利,即对应等差数列模型.
归纳总结
例2 某家庭打算以一年定期的方式存款,计划从2018年起,每年年初到银行新存入a元,年利率p保持不变,并按复利计算,到2028年年初将所有存款和利息全部取出,一共可以取回多少钱?
解:设从2018年年初到2028年年初每年存入a元的本利和组成数列{an}(1≤n≤10).
则a1=a(1+p)10,a2=a(1+p)9,…,a10=a(1+p),
故数列{an}(1≤n≤10)是以a1=a(1+p)10为首项,q=为公比的等比数列.
所以2028年初这个家庭应取出的钱数为
S10==[(1+p)11-(1+p)](元).
复利问题可以转化为等比数列问题,第n年的本息=本金×(1+利率)n.
归纳总结
例3 小张老师年初向银行贷款2万元用于买车,银行贷款的年利率为10%,按复利计算.若这笔贷款要分10年等额还清,每年年初还一次,并且从借款后次年年初开始归还,问每年应还多少元?(精确到1元)
解:设每年还款x元,需10年还清,则每年还款及利息情况如下:
第10年还款x元,此次欠款全部还清;
第9年还款x元,过1年欠款全部还清时,所付款连同利息之和为x(1+10%)元;
第8年还款x元,过2年欠款全部还清时,所付款连同利息之和为x(1+10%)2元;
……
第1年还款x元,过9年欠款全部还清时,所付款连同利息之和为x(1+10%)9元.
根据题意可得:
x+x(1+10%)+x(1+10%)2+…+x(1+10%)9=20 000(1+10%)10,
∴x=≈3 255.
∴每年应还款3 255元.
分期付款的相关规定:
(1)分期付款中,每期的利息均按复利计算,分期付款中规定每期所付款额相同;
(2)各期所付款额连同到最后一次付款时所产生的利息之和等于商品售价及从购买到最后一次付款时的利息之和(此为列方程的依据);
(3)每期付款增值后的款数及售价增值后的款数均按S=P(1+r)n来计算,其中P代表本金(可以是每期付款额x,也可以是商品售价),n代表存期(月数或年数),r代表利率,S代表本利和.
归纳总结
1.在分期付款中,期数增多,其他条件不变,每次付款额( )
A.增多 B.减少
C.不变 D.可增多也可减少
2.现存入银行10 000元钱,年利率是3.60%,那么按照复利,第5年末的本利和是( )
A.10 000×1.0363 B.10 000×1.0364
C.10 000×1.0365 D.10 000×1.0366
B
C
3.某人在一年12个月中,每月10日向银行存入1 000元,假设银行的月利率为5‰(按单利计算),则到第二年的元月10日,此项存款一年的利息之和是( )
A.5(1+2+3+…+12)元
B.5(1+2+3+…+11)元
C.1 000[1+5‰+(5‰)2+…+(5‰)11]元
D.1 000[1+5‰+(5‰)2+…+(5‰)12]元
A
同课章节目录
