2024-2025学年期末达标测试卷(含解析)-数学九年级上册北师大版
文档属性
| 名称 | 2024-2025学年期末达标测试卷(含解析)-数学九年级上册北师大版 |

|
|
| 格式 | docx | ||
| 文件大小 | 720.4KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-01-23 19:32:46 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
2024-2025学年期末达标测试卷-数学九年级上册北师大版
一.选择题(共10小题)
1.(2023秋 日照期末)在下列几何体中,主视图、左视图和俯视图形状都相同的是( )
A. B. C. D.
2.(2023秋 咸阳期末)若线段a,b,c,d是成比例线段,且a=1cm,b=4cm,c=2cm,则d=( )
A.8cm B.0.5cm C.2cm D.3cm
3.(2023秋 咸阳期末)如图,四边形ABCD的对角线AC,BD相交于点O,OA=OC,且AB∥CD,则添加下列一个条件能判定四边形ABCD是菱形的是( )
A.AC=BD B.∠ADB=∠CDB C.∠ABC=∠DCB D.AD=BC
4.(2023秋 永宁县期末)如图,在平行四边形ABCD中,E为边AD的中点,连接AC,BE交于点F.若△AEF的面积为2,则△ABC的面积为( )
A.8 B.10 C.12 D.14
5.(2023秋 蛟河市期末)若关于x的一元二次方程kx2+2x﹣1=0有实数根,则k的取值范围是( )
A.k≥﹣1且k≠0 B.k≥﹣1 C.k>﹣1 D.k>﹣1且k≠0
6.(2023秋 新罗区校级期末)已知点A(x1,y1),B(x2,y2),C(x3,y3)在反比例函数的图象上.其中x1<x2<0<x3.下列结论正确的是( )
A.y3<y1<y2 B.y1<y2<y3 C.y3<y2<y1 D.y2<y1<y3
7.(2023秋 绵阳期末)向阳村老李家2023年每月收入持续增长,若10月份收入为a元,12月份收入为b元.设平均每月收入的增长率为x,则方程可列为( )
A.a(1+x)=b B.a(1+x)2=b
C.a+a(1+x)2=b D.a+a(1+x)+a(1+x)2=b
8.(2023秋 绵阳期末)已知正比例函数y1=mx(m≠0)的图象与反比例函数的图象的一个交点坐标为(1,3),则不等式y1<y2的解集为( )
A.x<﹣1或x>1 B.x<﹣1或0<x<1
C.﹣1<x<1 D.﹣3<x<0或0<x<3
9.(2023秋 埇桥区校级期末)如图,△ABC∽△AED,若AD=3,AB=5,AC=6,则S△ABC:S△AED的值为( )
A.2:1 B.5:3 C.4:1 D.25:9
10.(2023秋 长春期末)如图,∠ACB=∠ADB=90°,E为AB的中点,AD与BC相交于点F.若∠CED=56°,则∠DCE的度数是( )
A.56° B.62° C.63° D.72°
二.填空题(共6小题)
11.(2023秋 绵阳期末)将反比例函数的图象向右平移1个单位长度,得到图象的解析式为 .
12.(2023秋 衡东县校级期末)在一张由复印机通过放大复印出来的纸上,一个面积为2cm2图案的一条边由原来的1cm变成4cm,则这次复印出来的图案的面积是 cm2.
13.(2023秋 咸阳期末)如图,△ABC和△DEF是以点O为位似中心的位似图形,,△ABC的周长为8,则△DEF的周长为 .
14.(2023秋 金台区校级期末)在矩形ABCD中,AB=10,BC=15,若点E是边CD的中点,连接AE,过点B作BF⊥AE于点F,则BF长为 .
15.(2023秋 兴文县期末)如图,在Rt△ABC中,∠BAC=90°,CD是△ABC的中线,E是CD的中点,连接AE,BE.若AE⊥BE,则∠ACE的度数为 .
16.(2023秋 临清市期末)如图,点A在反比例函数的图象上,以点A为圆心画弦交x轴于B,C,延长AC交y轴于点D,连接BD,若△BCD的面积等于4,BC=4OC,则k的值为 .
三.解答题(共9小题)
17.(2023秋 东坡区期末)解一元二次方程:2x2+x﹣6=0.
18.(2023秋 绵阳期末)产品质量是企业的生命,也是企业发展长远的根本,做好产品质量检测是一件非常重要的事情.某零件厂生产了5件规格一样的产品,因某道工序的不合理产生了2件次品,现从中不分先后一次性任意抽取3件进行检验.(记3件正品分别为A,B,C,2件次品分别为a,b)
(1)列出“从5件产品中不分先后一次性任意抽取3件产品”的所有等可能结果;
(2)求抽得的3件产品中至少含1件次品的概率.
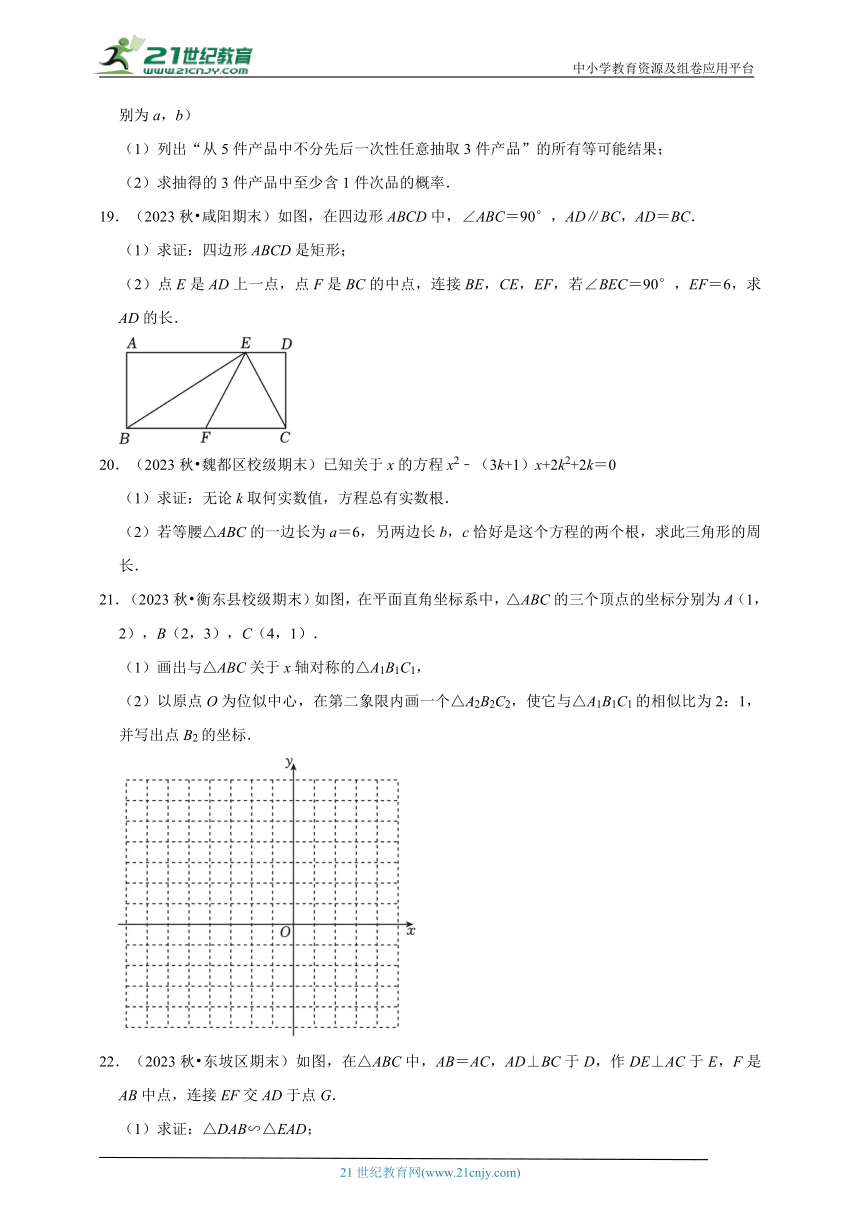
19.(2023秋 咸阳期末)如图,在四边形ABCD中,∠ABC=90°,AD∥BC,AD=BC.
(1)求证:四边形ABCD是矩形;
(2)点E是AD上一点,点F是BC的中点,连接BE,CE,EF,若∠BEC=90°,EF=6,求AD的长.
20.(2023秋 魏都区校级期末)已知关于x的方程x2﹣(3k+1)x+2k2+2k=0
(1)求证:无论k取何实数值,方程总有实数根.
(2)若等腰△ABC的一边长为a=6,另两边长b,c恰好是这个方程的两个根,求此三角形的周长.
21.(2023秋 衡东县校级期末)如图,在平面直角坐标系中,△ABC的三个顶点的坐标分别为A(1,2),B(2,3),C(4,1).
(1)画出与△ABC关于x轴对称的△A1B1C1,
(2)以原点O为位似中心,在第二象限内画一个△A2B2C2,使它与△A1B1C1的相似比为2:1,并写出点B2的坐标.
22.(2023秋 东坡区期末)如图,在△ABC中,AB=AC,AD⊥BC于D,作DE⊥AC于E,F是AB中点,连接EF交AD于点G.
(1)求证:△DAB∽△EAD;
(2)若AB=4,AE=3,求DG的值.
23.(2023秋 绵阳期末)如图,点A在第一象限,且在反比例函数的图象上,点B是点A关于x轴的对称点,△ABO的面积是4.
(1)求反比例函数的解析式;
(2)若点A的横坐标为1,延长AO交反比例函数的图象于点C,连接BC,点D(m,n)(m>1)在反比例函数图象上,满足△ACD的面积等于△ABC的面积,求直线BD的解析式.
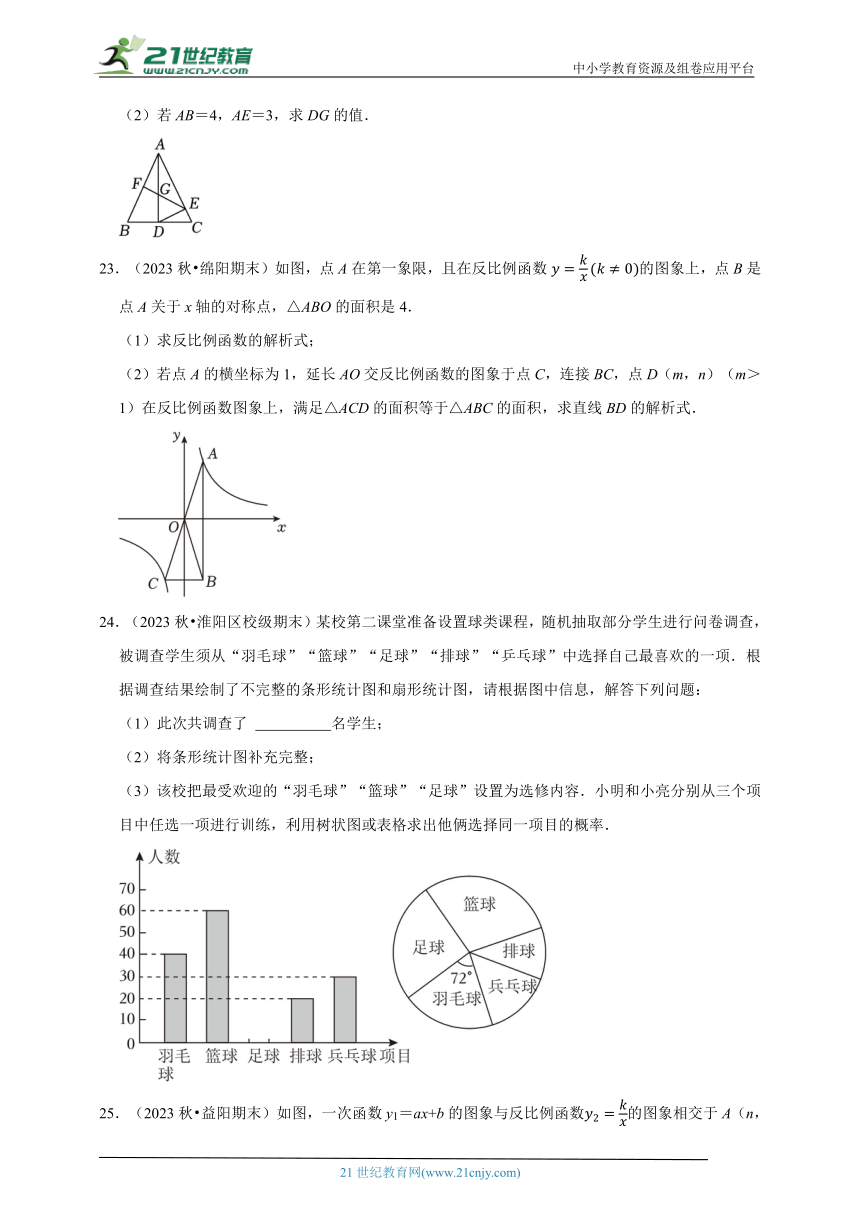
24.(2023秋 淮阳区校级期末)某校第二课堂准备设置球类课程,随机抽取部分学生进行问卷调查,被调查学生须从“羽毛球”“篮球”“足球”“排球”“乒乓球”中选择自己最喜欢的一项.根据调查结果绘制了不完整的条形统计图和扇形统计图,请根据图中信息,解答下列问题:
(1)此次共调查了 名学生;
(2)将条形统计图补充完整;
(3)该校把最受欢迎的“羽毛球”“篮球”“足球”设置为选修内容.小明和小亮分别从三个项目中任选一项进行训练,利用树状图或表格求出他俩选择同一项目的概率.
25.(2023秋 益阳期末)如图,一次函数y1=ax+b的图象与反比例函数的图象相交于A(n,3)和B(3,﹣1)两点,一次函数y1=ax+b图象分别与x轴,y轴交于E,D两点,过A作AC⊥x轴,垂足为C,连接OB.
(1)求一次函数解析式和反比例函数解析式.
(2)点P为反比例函数图象上一点,若S△BOD=S△PCE,求点P的坐标.
(3)直接写出不等式的解集.
2024-2025学年期末达标测试卷-数学九年级上册北师大版
参考答案与试题解析
题号 1 2 3 4 5 6 7 8 9 10
答案 C A B C A A B B C B
一.选择题(共10小题)
1.(2023秋 日照期末)在下列几何体中,主视图、左视图和俯视图形状都相同的是( )
A. B. C. D.
【解答】解:如图,球体的三视图都相同,都是圆形,
故选:C.
2.(2023秋 咸阳期末)若线段a,b,c,d是成比例线段,且a=1cm,b=4cm,c=2cm,则d=( )
A.8cm B.0.5cm C.2cm D.3cm
【解答】解:∵a,b,c,d是成比例线段,
∴ad=cb,
∵a=1cm,b=4cm,c=2cm,
∴d=8(cm),
故选:A.
3.(2023秋 咸阳期末)如图,四边形ABCD的对角线AC,BD相交于点O,OA=OC,且AB∥CD,则添加下列一个条件能判定四边形ABCD是菱形的是( )
A.AC=BD B.∠ADB=∠CDB C.∠ABC=∠DCB D.AD=BC
【解答】解:∵AB∥CD,
∴∠BAO=∠DCO,∠ABO=∠CDO,
∵OA=OC,
∴△AOB≌△COD(AAS),
∴AB=CD,
∴四边形ABCD是平行四边形,
A、当AC=BD时,四边形ABCD是矩形;故选项A不符合题意;
B、∵AB∥CD,
∴∠ABD=∠CDB,
∵∠ADB=∠CDB,
∴∠ADB=∠ABD,
∴AD=AB,
∴四边形ABCD为菱形,故选项B符合题意;
C、∵AB∥CD,
∴∠ABC+∠BCD=180°,
∵∠ABC=∠DCB
∴∠ABC=∠DCB=90°,
∴四边形ABCD是矩形;故选项C不符合题意;
D、当AD=BC时,不能判定四边形ABCD为菱形;故选项D不符合题意.
故选:B.
4.(2023秋 永宁县期末)如图,在平行四边形ABCD中,E为边AD的中点,连接AC,BE交于点F.若△AEF的面积为2,则△ABC的面积为( )
A.8 B.10 C.12 D.14
【解答】解:如图,∵四边形ABCD是平行四边形,
∵EA∥BC,
∴△AEF∽△CBF,
∵AE=DEAD,CB=AD,
∴,
∴AFAC,EFBF,
∴S△ABFS△ABC,
∴S△AEFS△ABFS△ABCS△ABC,
∵S△AEF=2,
∴S△ABC=6S△AEF=6×2=12,
故选:C.
5.(2023秋 蛟河市期末)若关于x的一元二次方程kx2+2x﹣1=0有实数根,则k的取值范围是( )
A.k≥﹣1且k≠0 B.k≥﹣1 C.k>﹣1 D.k>﹣1且k≠0
【解答】解:根据题意得k≠0且Δ=22﹣4k×(﹣1)≥0,
解得k≥﹣1且k≠0.
故选:A.
6.(2023秋 新罗区校级期末)已知点A(x1,y1),B(x2,y2),C(x3,y3)在反比例函数的图象上.其中x1<x2<0<x3.下列结论正确的是( )
A.y3<y1<y2 B.y1<y2<y3 C.y3<y2<y1 D.y2<y1<y3
【解答】解:∵反比例函数,
∴函数图象在第二、四象限,在每个象限内,y随着x的增大而增大,
又∵x1<x2<0<x3,
∴y1>0,y2>0,y3<0,y1<y2,
∴y3<y1<y2,
故选:A.
7.(2023秋 绵阳期末)向阳村老李家2023年每月收入持续增长,若10月份收入为a元,12月份收入为b元.设平均每月收入的增长率为x,则方程可列为( )
A.a(1+x)=b B.a(1+x)2=b
C.a+a(1+x)2=b D.a+a(1+x)+a(1+x)2=b
【解答】解:设平均每月收入的增长率为x,则方程可列为a(1+x)2=b,
故选:B.
8.(2023秋 绵阳期末)已知正比例函数y1=mx(m≠0)的图象与反比例函数的图象的一个交点坐标为(1,3),则不等式y1<y2的解集为( )
A.x<﹣1或x>1 B.x<﹣1或0<x<1
C.﹣1<x<1 D.﹣3<x<0或0<x<3
【解答】解:∵正比例函数y1=mx(m≠0)的图象与反比例函数的图象的一个交点坐标为(1,3),
∴m=3,n=1×3=3,
∴正比例函数y1=3x,反比例函数,
画出函数图象如图所示:
由图象可得:不等式y1<y2的解集为x<﹣1或0<x<1,
故选:B.
9.(2023秋 埇桥区校级期末)如图,△ABC∽△AED,若AD=3,AB=5,AC=6,则S△ABC:S△AED的值为( )
A.2:1 B.5:3 C.4:1 D.25:9
【解答】解:∵△ABC∽△AED,AD=3,AC=6,
∴,
∴S△ABC:S△AED=()2=4:1.
故选:C.
10.(2023秋 长春期末)如图,∠ACB=∠ADB=90°,E为AB的中点,AD与BC相交于点F.若∠CED=56°,则∠DCE的度数是( )
A.56° B.62° C.63° D.72°
【解答】解:∵∠ACB=∠ADB=90°,E为AB的中点,
∴△ACB和△ADB均为直角三角形,且点E是公共斜边AB的中点,
∴EC=EDAB,
∴∠DCE=∠CDE,
∵∠CED=56°,∠CED+∠DCE+∠CDE=180°,
∴∠DCE=62°,
故选:B.
二.填空题(共6小题)
11.(2023秋 绵阳期末)将反比例函数的图象向右平移1个单位长度,得到图象的解析式为 .
【解答】解:设平移后函数的图象上任一点坐标为(m,n),
因为将平移后的函数图象向左平移1个单位长度,得到反比例函数的图象,
则(m,n)向左平移1个单位后得到(m﹣1,n),其在函数图象上,
将(m﹣1,n)代入,得,
故将反比例函数的图象向右平移1个单位长度,得到图象的解析式为,
故答案为:.
12.(2023秋 衡东县校级期末)在一张由复印机通过放大复印出来的纸上,一个面积为2cm2图案的一条边由原来的1cm变成4cm,则这次复印出来的图案的面积是 32 cm2.
【解答】解:∵在一张由复印机通过放大复印出来的纸上,一个面积为2cm2图案的一条边由原来的1cm变成4cm,
∴相似比,
∴面积比,
∴这次复印出来的图案的面积=2×16=32(cm2).
故答案是:32.
13.(2023秋 咸阳期末)如图,△ABC和△DEF是以点O为位似中心的位似图形,,△ABC的周长为8,则△DEF的周长为 20 .
【解答】解:∵△ABC和△DEF是以点O为位似中心的位似图形,
∴△ABC∽△DEF,AB∥DE,
∴△AOB∽△DOE,
∴,
∴,
∵△ABC的周长为8,
∴,
解得:C△DEF=20.
故答案为:20.
14.(2023秋 金台区校级期末)在矩形ABCD中,AB=10,BC=15,若点E是边CD的中点,连接AE,过点B作BF⊥AE于点F,则BF长为 .
【解答】解:如图,连接BE,
在矩形ABCD中,∵AB=10,BC=15,
CD=AB=10,AD=BC=15,∠C=∠D=90°,
∵E是边CD的中点,
∴,
∴,,
S△ADE+S△BCE+S△ABE=S矩形ABCD,
∴,
即,
解得,
故答案为:.
15.(2023秋 兴文县期末)如图,在Rt△ABC中,∠BAC=90°,CD是△ABC的中线,E是CD的中点,连接AE,BE.若AE⊥BE,则∠ACE的度数为 30° .
【解答】解:∵AE⊥BE,
∴∠AEB=90°,
∵点D是AB的中点,
∴ED=AD,
∵∠DAC=90°,E是CD的中点,
∴AE=DE,
∴AD=DE=AE,
∴△ADE是等边三角形,
∴∠ADE=60°,
∴∠ACE=90°﹣∠ADC=30°,
故答案为:30°.
16.(2023秋 临清市期末)如图,点A在反比例函数的图象上,以点A为圆心画弦交x轴于B,C,延长AC交y轴于点D,连接BD,若△BCD的面积等于4,BC=4OC,则k的值为 12 .
【解答】解:作AE⊥BC于E,连接OA,
∵以点A为圆心画弧交x轴于点B、C,
∴AB=AC,
∴,
∵BC=4OC,
∴,
∵AE∥OD,
∴△COD∽△CEA,
∴,
∵△BCD的面积等于4,OB=OC+BC=5OC,
∴,
∴S△CEA=4S△COD=4×1=4
∵,
∴,
∴S△AOE=2+4=6,
∵,
∵k>0,
∴k=12,
故答案为:12.
三.解答题(共9小题)
17.(2023秋 东坡区期末)解一元二次方程:2x2+x﹣6=0.
【解答】解:2x2+x﹣6=0,
(2x﹣3)(x+2)=0,
2x﹣3=0,x+2=0,
x1,x2=﹣2.
18.(2023秋 绵阳期末)产品质量是企业的生命,也是企业发展长远的根本,做好产品质量检测是一件非常重要的事情.某零件厂生产了5件规格一样的产品,因某道工序的不合理产生了2件次品,现从中不分先后一次性任意抽取3件进行检验.(记3件正品分别为A,B,C,2件次品分别为a,b)
(1)列出“从5件产品中不分先后一次性任意抽取3件产品”的所有等可能结果;
(2)求抽得的3件产品中至少含1件次品的概率.
【解答】解:(1)从5件产品中不分先后一次性任意抽取3件的所有等可能的结果有ABC,ABa,ABb,ACa,ACb,Aab,BCa,BCb,Bab,Cab.
(2)由(1)得基本事件的总数为m=10,
其中抽取的3件产品中没有次品的结果有n=1种.
∴抽得的3件产品中至少含1件次品的概率为.
19.(2023秋 咸阳期末)如图,在四边形ABCD中,∠ABC=90°,AD∥BC,AD=BC.
(1)求证:四边形ABCD是矩形;
(2)点E是AD上一点,点F是BC的中点,连接BE,CE,EF,若∠BEC=90°,EF=6,求AD的长.
【解答】(1)证明:∵AD∥BC,AD=BC,
∴四边形ABCD是平行四边形.
∵∠ABC=90°,
∴四边形ABCD是矩形.
(2)解:∵∠BEC=90°,点F是BC的中点,
∴,
∴BC=12,
∴AD=BC=12.
20.(2023秋 魏都区校级期末)已知关于x的方程x2﹣(3k+1)x+2k2+2k=0
(1)求证:无论k取何实数值,方程总有实数根.
(2)若等腰△ABC的一边长为a=6,另两边长b,c恰好是这个方程的两个根,求此三角形的周长.
【解答】(1)证明:Δ=[﹣(3k+1)]2﹣4×1×(2k2+2k),
=k2﹣2k+1,
=(k﹣1)2,
∵无论k取什么实数值,(k﹣1)2≥0,
∴△≥0,
所以无论k取什么实数值,方程总有实数根;
(2)x2﹣(3k+1)x+2k2+2k=0,
因式分解得:(x﹣2k)(x﹣k﹣1)=0,
解得:x1=2k,x2=k+1,
∵b,c恰好是这个方程的两个实数根,设b=2k,c=k+1,
当a、b为腰,则a=b=6,而a+b>c,a﹣b<c,所以三角形的周长为:6+6+4=16;
当b、c为腰,则k+1=2k,解得k=1,
∴b=c=2,因为6,2,2不构成三角形,∴所以这种情况不成立;
当a、c为腰 k+1=6 则k=5,
∴b=10,
∴三角形的周长为:6+6+10=22.
综上,三角形的周长为16或22.
21.(2023秋 衡东县校级期末)如图,在平面直角坐标系中,△ABC的三个顶点的坐标分别为A(1,2),B(2,3),C(4,1).
(1)画出与△ABC关于x轴对称的△A1B1C1,
(2)以原点O为位似中心,在第二象限内画一个△A2B2C2,使它与△A1B1C1的相似比为2:1,并写出点B2的坐标.
【解答】解:(1)如图所示,△A1B1C1为所作;
(2)如图所示,△A2B2C2为所作,点B2的坐标为(﹣4,6).
22.(2023秋 东坡区期末)如图,在△ABC中,AB=AC,AD⊥BC于D,作DE⊥AC于E,F是AB中点,连接EF交AD于点G.
(1)求证:△DAB∽△EAD;
(2)若AB=4,AE=3,求DG的值.
【解答】(1)证明:∵AB=AC,AD⊥BC,
∴∠BAD=∠DAE,
∵DE⊥AC,
∴∠ADB=∠AED=90°,
∴△DAB∽△EAD.
(2)解:∵△ABD∽△ADE,
∴,而AB=4,AE=3,
∴AD2=AB AE=3×4=12,
∴,
如图,连接DF,
∵AB=AC=4,AD⊥BC,
∴D为BC中点,
∵F为AB中点,
∴DF为△ABC中位线,
∴DF∥AC,,
∴△DGF∽△AGE,
∴,即,
∴,
∴,即,
解得;
∴DG的值为.
23.(2023秋 绵阳期末)如图,点A在第一象限,且在反比例函数的图象上,点B是点A关于x轴的对称点,△ABO的面积是4.
(1)求反比例函数的解析式;
(2)若点A的横坐标为1,延长AO交反比例函数的图象于点C,连接BC,点D(m,n)(m>1)在反比例函数图象上,满足△ACD的面积等于△ABC的面积,求直线BD的解析式.
【解答】解:(1)如图,设AB与x轴交于点E.
∵B是点A关于x轴的对称点,△ABO的面积是4,
∴S△AOE=2.
∴,即AE EO=4.
又AE EO=k.
∴k=4.
∴反比例函数的解析式.
(2)∵点A的横坐标为1,
当x=1时,y=4,
∴A(1,4).
由点A与点B关于x轴对称得B(1,﹣4).
由题可得,点A与点C关于原点O对称,
∴C(﹣1,﹣4),
过B点作BD∥AC,直线BD与反比例函数在第一象限的图象的交点为所求点D,
∴S△ADC=S△ABC.
设直线AC的解析式为y=ax(a≠0).
将A(1,4)代入上式,得a=4,
∴直线AC解析式为y=4x.
∵AC∥BD,
∴可设直线BD的解析式为y=4x+b,
将B(1,﹣4)代入上式,得到﹣4=4+b,
解得b=﹣8.
∴直线BD的解析式为y=4x﹣8.
24.(2023秋 淮阳区校级期末)某校第二课堂准备设置球类课程,随机抽取部分学生进行问卷调查,被调查学生须从“羽毛球”“篮球”“足球”“排球”“乒乓球”中选择自己最喜欢的一项.根据调查结果绘制了不完整的条形统计图和扇形统计图,请根据图中信息,解答下列问题:
(1)此次共调查了 200 名学生;
(2)将条形统计图补充完整;
(3)该校把最受欢迎的“羽毛球”“篮球”“足球”设置为选修内容.小明和小亮分别从三个项目中任选一项进行训练,利用树状图或表格求出他俩选择同一项目的概率.
【解答】解:(1)此次共调查的学生有:(名);
(2)足球的人数有:200﹣40﹣60﹣20﹣30=50(名),补全统计图如图1:
(3)设“羽毛球”“篮球”“足球”分别为A、B、C,根据题意画树状图如图2:
共有9种等可能的情况,其中他俩选择相同项目的有3种,
则P(他俩选择相同项目).
25.(2023秋 益阳期末)如图,一次函数y1=ax+b的图象与反比例函数的图象相交于A(n,3)和B(3,﹣1)两点,一次函数y1=ax+b图象分别与x轴,y轴交于E,D两点,过A作AC⊥x轴,垂足为C,连接OB.
(1)求一次函数解析式和反比例函数解析式.
(2)点P为反比例函数图象上一点,若S△BOD=S△PCE,求点P的坐标.
(3)直接写出不等式的解集.
【解答】解:(1)将点B(3,﹣1)代入,得:k=3×(﹣1)=﹣3,
则反比例函数解析式为y,
∵反比例函数的图象过A(n,3),
∴3,
∴n=﹣1,
∴A(﹣1,3),
将点A(﹣1,3)、B(3,﹣1)代入y=ax+b得,
解得,
则一次函数解析式为y=﹣x+2;
(2)令x=0,则y=﹣x+2=2,
∴D(0,2),
令y=0,则﹣x+2=0,解得x=2,
∴E(2,0),
∴S△BOD3,
∵AC⊥x轴,垂足为C,
∴C(﹣1,0),
∴CE=3,
∵S△BOD=S△PCE,
∴,
∴,
∴yP=±2,
把y=2代入y得到,x,
把y=﹣2代入y得到,x,
∴点P的坐标为(,2)或(,﹣2).
(3)∵一次函数y1=ax+b的图象与反比例函数的图象相交于A(﹣1,3)和B(3,﹣1)两点,
由图象可得,﹣1<x<0或x>3时,ax+b.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
2024-2025学年期末达标测试卷-数学九年级上册北师大版
一.选择题(共10小题)
1.(2023秋 日照期末)在下列几何体中,主视图、左视图和俯视图形状都相同的是( )
A. B. C. D.
2.(2023秋 咸阳期末)若线段a,b,c,d是成比例线段,且a=1cm,b=4cm,c=2cm,则d=( )
A.8cm B.0.5cm C.2cm D.3cm
3.(2023秋 咸阳期末)如图,四边形ABCD的对角线AC,BD相交于点O,OA=OC,且AB∥CD,则添加下列一个条件能判定四边形ABCD是菱形的是( )
A.AC=BD B.∠ADB=∠CDB C.∠ABC=∠DCB D.AD=BC
4.(2023秋 永宁县期末)如图,在平行四边形ABCD中,E为边AD的中点,连接AC,BE交于点F.若△AEF的面积为2,则△ABC的面积为( )
A.8 B.10 C.12 D.14
5.(2023秋 蛟河市期末)若关于x的一元二次方程kx2+2x﹣1=0有实数根,则k的取值范围是( )
A.k≥﹣1且k≠0 B.k≥﹣1 C.k>﹣1 D.k>﹣1且k≠0
6.(2023秋 新罗区校级期末)已知点A(x1,y1),B(x2,y2),C(x3,y3)在反比例函数的图象上.其中x1<x2<0<x3.下列结论正确的是( )
A.y3<y1<y2 B.y1<y2<y3 C.y3<y2<y1 D.y2<y1<y3
7.(2023秋 绵阳期末)向阳村老李家2023年每月收入持续增长,若10月份收入为a元,12月份收入为b元.设平均每月收入的增长率为x,则方程可列为( )
A.a(1+x)=b B.a(1+x)2=b
C.a+a(1+x)2=b D.a+a(1+x)+a(1+x)2=b
8.(2023秋 绵阳期末)已知正比例函数y1=mx(m≠0)的图象与反比例函数的图象的一个交点坐标为(1,3),则不等式y1<y2的解集为( )
A.x<﹣1或x>1 B.x<﹣1或0<x<1
C.﹣1<x<1 D.﹣3<x<0或0<x<3
9.(2023秋 埇桥区校级期末)如图,△ABC∽△AED,若AD=3,AB=5,AC=6,则S△ABC:S△AED的值为( )
A.2:1 B.5:3 C.4:1 D.25:9
10.(2023秋 长春期末)如图,∠ACB=∠ADB=90°,E为AB的中点,AD与BC相交于点F.若∠CED=56°,则∠DCE的度数是( )
A.56° B.62° C.63° D.72°
二.填空题(共6小题)
11.(2023秋 绵阳期末)将反比例函数的图象向右平移1个单位长度,得到图象的解析式为 .
12.(2023秋 衡东县校级期末)在一张由复印机通过放大复印出来的纸上,一个面积为2cm2图案的一条边由原来的1cm变成4cm,则这次复印出来的图案的面积是 cm2.
13.(2023秋 咸阳期末)如图,△ABC和△DEF是以点O为位似中心的位似图形,,△ABC的周长为8,则△DEF的周长为 .
14.(2023秋 金台区校级期末)在矩形ABCD中,AB=10,BC=15,若点E是边CD的中点,连接AE,过点B作BF⊥AE于点F,则BF长为 .
15.(2023秋 兴文县期末)如图,在Rt△ABC中,∠BAC=90°,CD是△ABC的中线,E是CD的中点,连接AE,BE.若AE⊥BE,则∠ACE的度数为 .
16.(2023秋 临清市期末)如图,点A在反比例函数的图象上,以点A为圆心画弦交x轴于B,C,延长AC交y轴于点D,连接BD,若△BCD的面积等于4,BC=4OC,则k的值为 .
三.解答题(共9小题)
17.(2023秋 东坡区期末)解一元二次方程:2x2+x﹣6=0.
18.(2023秋 绵阳期末)产品质量是企业的生命,也是企业发展长远的根本,做好产品质量检测是一件非常重要的事情.某零件厂生产了5件规格一样的产品,因某道工序的不合理产生了2件次品,现从中不分先后一次性任意抽取3件进行检验.(记3件正品分别为A,B,C,2件次品分别为a,b)
(1)列出“从5件产品中不分先后一次性任意抽取3件产品”的所有等可能结果;
(2)求抽得的3件产品中至少含1件次品的概率.
19.(2023秋 咸阳期末)如图,在四边形ABCD中,∠ABC=90°,AD∥BC,AD=BC.
(1)求证:四边形ABCD是矩形;
(2)点E是AD上一点,点F是BC的中点,连接BE,CE,EF,若∠BEC=90°,EF=6,求AD的长.
20.(2023秋 魏都区校级期末)已知关于x的方程x2﹣(3k+1)x+2k2+2k=0
(1)求证:无论k取何实数值,方程总有实数根.
(2)若等腰△ABC的一边长为a=6,另两边长b,c恰好是这个方程的两个根,求此三角形的周长.
21.(2023秋 衡东县校级期末)如图,在平面直角坐标系中,△ABC的三个顶点的坐标分别为A(1,2),B(2,3),C(4,1).
(1)画出与△ABC关于x轴对称的△A1B1C1,
(2)以原点O为位似中心,在第二象限内画一个△A2B2C2,使它与△A1B1C1的相似比为2:1,并写出点B2的坐标.
22.(2023秋 东坡区期末)如图,在△ABC中,AB=AC,AD⊥BC于D,作DE⊥AC于E,F是AB中点,连接EF交AD于点G.
(1)求证:△DAB∽△EAD;
(2)若AB=4,AE=3,求DG的值.
23.(2023秋 绵阳期末)如图,点A在第一象限,且在反比例函数的图象上,点B是点A关于x轴的对称点,△ABO的面积是4.
(1)求反比例函数的解析式;
(2)若点A的横坐标为1,延长AO交反比例函数的图象于点C,连接BC,点D(m,n)(m>1)在反比例函数图象上,满足△ACD的面积等于△ABC的面积,求直线BD的解析式.
24.(2023秋 淮阳区校级期末)某校第二课堂准备设置球类课程,随机抽取部分学生进行问卷调查,被调查学生须从“羽毛球”“篮球”“足球”“排球”“乒乓球”中选择自己最喜欢的一项.根据调查结果绘制了不完整的条形统计图和扇形统计图,请根据图中信息,解答下列问题:
(1)此次共调查了 名学生;
(2)将条形统计图补充完整;
(3)该校把最受欢迎的“羽毛球”“篮球”“足球”设置为选修内容.小明和小亮分别从三个项目中任选一项进行训练,利用树状图或表格求出他俩选择同一项目的概率.
25.(2023秋 益阳期末)如图,一次函数y1=ax+b的图象与反比例函数的图象相交于A(n,3)和B(3,﹣1)两点,一次函数y1=ax+b图象分别与x轴,y轴交于E,D两点,过A作AC⊥x轴,垂足为C,连接OB.
(1)求一次函数解析式和反比例函数解析式.
(2)点P为反比例函数图象上一点,若S△BOD=S△PCE,求点P的坐标.
(3)直接写出不等式的解集.
2024-2025学年期末达标测试卷-数学九年级上册北师大版
参考答案与试题解析
题号 1 2 3 4 5 6 7 8 9 10
答案 C A B C A A B B C B
一.选择题(共10小题)
1.(2023秋 日照期末)在下列几何体中,主视图、左视图和俯视图形状都相同的是( )
A. B. C. D.
【解答】解:如图,球体的三视图都相同,都是圆形,
故选:C.
2.(2023秋 咸阳期末)若线段a,b,c,d是成比例线段,且a=1cm,b=4cm,c=2cm,则d=( )
A.8cm B.0.5cm C.2cm D.3cm
【解答】解:∵a,b,c,d是成比例线段,
∴ad=cb,
∵a=1cm,b=4cm,c=2cm,
∴d=8(cm),
故选:A.
3.(2023秋 咸阳期末)如图,四边形ABCD的对角线AC,BD相交于点O,OA=OC,且AB∥CD,则添加下列一个条件能判定四边形ABCD是菱形的是( )
A.AC=BD B.∠ADB=∠CDB C.∠ABC=∠DCB D.AD=BC
【解答】解:∵AB∥CD,
∴∠BAO=∠DCO,∠ABO=∠CDO,
∵OA=OC,
∴△AOB≌△COD(AAS),
∴AB=CD,
∴四边形ABCD是平行四边形,
A、当AC=BD时,四边形ABCD是矩形;故选项A不符合题意;
B、∵AB∥CD,
∴∠ABD=∠CDB,
∵∠ADB=∠CDB,
∴∠ADB=∠ABD,
∴AD=AB,
∴四边形ABCD为菱形,故选项B符合题意;
C、∵AB∥CD,
∴∠ABC+∠BCD=180°,
∵∠ABC=∠DCB
∴∠ABC=∠DCB=90°,
∴四边形ABCD是矩形;故选项C不符合题意;
D、当AD=BC时,不能判定四边形ABCD为菱形;故选项D不符合题意.
故选:B.
4.(2023秋 永宁县期末)如图,在平行四边形ABCD中,E为边AD的中点,连接AC,BE交于点F.若△AEF的面积为2,则△ABC的面积为( )
A.8 B.10 C.12 D.14
【解答】解:如图,∵四边形ABCD是平行四边形,
∵EA∥BC,
∴△AEF∽△CBF,
∵AE=DEAD,CB=AD,
∴,
∴AFAC,EFBF,
∴S△ABFS△ABC,
∴S△AEFS△ABFS△ABCS△ABC,
∵S△AEF=2,
∴S△ABC=6S△AEF=6×2=12,
故选:C.
5.(2023秋 蛟河市期末)若关于x的一元二次方程kx2+2x﹣1=0有实数根,则k的取值范围是( )
A.k≥﹣1且k≠0 B.k≥﹣1 C.k>﹣1 D.k>﹣1且k≠0
【解答】解:根据题意得k≠0且Δ=22﹣4k×(﹣1)≥0,
解得k≥﹣1且k≠0.
故选:A.
6.(2023秋 新罗区校级期末)已知点A(x1,y1),B(x2,y2),C(x3,y3)在反比例函数的图象上.其中x1<x2<0<x3.下列结论正确的是( )
A.y3<y1<y2 B.y1<y2<y3 C.y3<y2<y1 D.y2<y1<y3
【解答】解:∵反比例函数,
∴函数图象在第二、四象限,在每个象限内,y随着x的增大而增大,
又∵x1<x2<0<x3,
∴y1>0,y2>0,y3<0,y1<y2,
∴y3<y1<y2,
故选:A.
7.(2023秋 绵阳期末)向阳村老李家2023年每月收入持续增长,若10月份收入为a元,12月份收入为b元.设平均每月收入的增长率为x,则方程可列为( )
A.a(1+x)=b B.a(1+x)2=b
C.a+a(1+x)2=b D.a+a(1+x)+a(1+x)2=b
【解答】解:设平均每月收入的增长率为x,则方程可列为a(1+x)2=b,
故选:B.
8.(2023秋 绵阳期末)已知正比例函数y1=mx(m≠0)的图象与反比例函数的图象的一个交点坐标为(1,3),则不等式y1<y2的解集为( )
A.x<﹣1或x>1 B.x<﹣1或0<x<1
C.﹣1<x<1 D.﹣3<x<0或0<x<3
【解答】解:∵正比例函数y1=mx(m≠0)的图象与反比例函数的图象的一个交点坐标为(1,3),
∴m=3,n=1×3=3,
∴正比例函数y1=3x,反比例函数,
画出函数图象如图所示:
由图象可得:不等式y1<y2的解集为x<﹣1或0<x<1,
故选:B.
9.(2023秋 埇桥区校级期末)如图,△ABC∽△AED,若AD=3,AB=5,AC=6,则S△ABC:S△AED的值为( )
A.2:1 B.5:3 C.4:1 D.25:9
【解答】解:∵△ABC∽△AED,AD=3,AC=6,
∴,
∴S△ABC:S△AED=()2=4:1.
故选:C.
10.(2023秋 长春期末)如图,∠ACB=∠ADB=90°,E为AB的中点,AD与BC相交于点F.若∠CED=56°,则∠DCE的度数是( )
A.56° B.62° C.63° D.72°
【解答】解:∵∠ACB=∠ADB=90°,E为AB的中点,
∴△ACB和△ADB均为直角三角形,且点E是公共斜边AB的中点,
∴EC=EDAB,
∴∠DCE=∠CDE,
∵∠CED=56°,∠CED+∠DCE+∠CDE=180°,
∴∠DCE=62°,
故选:B.
二.填空题(共6小题)
11.(2023秋 绵阳期末)将反比例函数的图象向右平移1个单位长度,得到图象的解析式为 .
【解答】解:设平移后函数的图象上任一点坐标为(m,n),
因为将平移后的函数图象向左平移1个单位长度,得到反比例函数的图象,
则(m,n)向左平移1个单位后得到(m﹣1,n),其在函数图象上,
将(m﹣1,n)代入,得,
故将反比例函数的图象向右平移1个单位长度,得到图象的解析式为,
故答案为:.
12.(2023秋 衡东县校级期末)在一张由复印机通过放大复印出来的纸上,一个面积为2cm2图案的一条边由原来的1cm变成4cm,则这次复印出来的图案的面积是 32 cm2.
【解答】解:∵在一张由复印机通过放大复印出来的纸上,一个面积为2cm2图案的一条边由原来的1cm变成4cm,
∴相似比,
∴面积比,
∴这次复印出来的图案的面积=2×16=32(cm2).
故答案是:32.
13.(2023秋 咸阳期末)如图,△ABC和△DEF是以点O为位似中心的位似图形,,△ABC的周长为8,则△DEF的周长为 20 .
【解答】解:∵△ABC和△DEF是以点O为位似中心的位似图形,
∴△ABC∽△DEF,AB∥DE,
∴△AOB∽△DOE,
∴,
∴,
∵△ABC的周长为8,
∴,
解得:C△DEF=20.
故答案为:20.
14.(2023秋 金台区校级期末)在矩形ABCD中,AB=10,BC=15,若点E是边CD的中点,连接AE,过点B作BF⊥AE于点F,则BF长为 .
【解答】解:如图,连接BE,
在矩形ABCD中,∵AB=10,BC=15,
CD=AB=10,AD=BC=15,∠C=∠D=90°,
∵E是边CD的中点,
∴,
∴,,
S△ADE+S△BCE+S△ABE=S矩形ABCD,
∴,
即,
解得,
故答案为:.
15.(2023秋 兴文县期末)如图,在Rt△ABC中,∠BAC=90°,CD是△ABC的中线,E是CD的中点,连接AE,BE.若AE⊥BE,则∠ACE的度数为 30° .
【解答】解:∵AE⊥BE,
∴∠AEB=90°,
∵点D是AB的中点,
∴ED=AD,
∵∠DAC=90°,E是CD的中点,
∴AE=DE,
∴AD=DE=AE,
∴△ADE是等边三角形,
∴∠ADE=60°,
∴∠ACE=90°﹣∠ADC=30°,
故答案为:30°.
16.(2023秋 临清市期末)如图,点A在反比例函数的图象上,以点A为圆心画弦交x轴于B,C,延长AC交y轴于点D,连接BD,若△BCD的面积等于4,BC=4OC,则k的值为 12 .
【解答】解:作AE⊥BC于E,连接OA,
∵以点A为圆心画弧交x轴于点B、C,
∴AB=AC,
∴,
∵BC=4OC,
∴,
∵AE∥OD,
∴△COD∽△CEA,
∴,
∵△BCD的面积等于4,OB=OC+BC=5OC,
∴,
∴S△CEA=4S△COD=4×1=4
∵,
∴,
∴S△AOE=2+4=6,
∵,
∵k>0,
∴k=12,
故答案为:12.
三.解答题(共9小题)
17.(2023秋 东坡区期末)解一元二次方程:2x2+x﹣6=0.
【解答】解:2x2+x﹣6=0,
(2x﹣3)(x+2)=0,
2x﹣3=0,x+2=0,
x1,x2=﹣2.
18.(2023秋 绵阳期末)产品质量是企业的生命,也是企业发展长远的根本,做好产品质量检测是一件非常重要的事情.某零件厂生产了5件规格一样的产品,因某道工序的不合理产生了2件次品,现从中不分先后一次性任意抽取3件进行检验.(记3件正品分别为A,B,C,2件次品分别为a,b)
(1)列出“从5件产品中不分先后一次性任意抽取3件产品”的所有等可能结果;
(2)求抽得的3件产品中至少含1件次品的概率.
【解答】解:(1)从5件产品中不分先后一次性任意抽取3件的所有等可能的结果有ABC,ABa,ABb,ACa,ACb,Aab,BCa,BCb,Bab,Cab.
(2)由(1)得基本事件的总数为m=10,
其中抽取的3件产品中没有次品的结果有n=1种.
∴抽得的3件产品中至少含1件次品的概率为.
19.(2023秋 咸阳期末)如图,在四边形ABCD中,∠ABC=90°,AD∥BC,AD=BC.
(1)求证:四边形ABCD是矩形;
(2)点E是AD上一点,点F是BC的中点,连接BE,CE,EF,若∠BEC=90°,EF=6,求AD的长.
【解答】(1)证明:∵AD∥BC,AD=BC,
∴四边形ABCD是平行四边形.
∵∠ABC=90°,
∴四边形ABCD是矩形.
(2)解:∵∠BEC=90°,点F是BC的中点,
∴,
∴BC=12,
∴AD=BC=12.
20.(2023秋 魏都区校级期末)已知关于x的方程x2﹣(3k+1)x+2k2+2k=0
(1)求证:无论k取何实数值,方程总有实数根.
(2)若等腰△ABC的一边长为a=6,另两边长b,c恰好是这个方程的两个根,求此三角形的周长.
【解答】(1)证明:Δ=[﹣(3k+1)]2﹣4×1×(2k2+2k),
=k2﹣2k+1,
=(k﹣1)2,
∵无论k取什么实数值,(k﹣1)2≥0,
∴△≥0,
所以无论k取什么实数值,方程总有实数根;
(2)x2﹣(3k+1)x+2k2+2k=0,
因式分解得:(x﹣2k)(x﹣k﹣1)=0,
解得:x1=2k,x2=k+1,
∵b,c恰好是这个方程的两个实数根,设b=2k,c=k+1,
当a、b为腰,则a=b=6,而a+b>c,a﹣b<c,所以三角形的周长为:6+6+4=16;
当b、c为腰,则k+1=2k,解得k=1,
∴b=c=2,因为6,2,2不构成三角形,∴所以这种情况不成立;
当a、c为腰 k+1=6 则k=5,
∴b=10,
∴三角形的周长为:6+6+10=22.
综上,三角形的周长为16或22.
21.(2023秋 衡东县校级期末)如图,在平面直角坐标系中,△ABC的三个顶点的坐标分别为A(1,2),B(2,3),C(4,1).
(1)画出与△ABC关于x轴对称的△A1B1C1,
(2)以原点O为位似中心,在第二象限内画一个△A2B2C2,使它与△A1B1C1的相似比为2:1,并写出点B2的坐标.
【解答】解:(1)如图所示,△A1B1C1为所作;
(2)如图所示,△A2B2C2为所作,点B2的坐标为(﹣4,6).
22.(2023秋 东坡区期末)如图,在△ABC中,AB=AC,AD⊥BC于D,作DE⊥AC于E,F是AB中点,连接EF交AD于点G.
(1)求证:△DAB∽△EAD;
(2)若AB=4,AE=3,求DG的值.
【解答】(1)证明:∵AB=AC,AD⊥BC,
∴∠BAD=∠DAE,
∵DE⊥AC,
∴∠ADB=∠AED=90°,
∴△DAB∽△EAD.
(2)解:∵△ABD∽△ADE,
∴,而AB=4,AE=3,
∴AD2=AB AE=3×4=12,
∴,
如图,连接DF,
∵AB=AC=4,AD⊥BC,
∴D为BC中点,
∵F为AB中点,
∴DF为△ABC中位线,
∴DF∥AC,,
∴△DGF∽△AGE,
∴,即,
∴,
∴,即,
解得;
∴DG的值为.
23.(2023秋 绵阳期末)如图,点A在第一象限,且在反比例函数的图象上,点B是点A关于x轴的对称点,△ABO的面积是4.
(1)求反比例函数的解析式;
(2)若点A的横坐标为1,延长AO交反比例函数的图象于点C,连接BC,点D(m,n)(m>1)在反比例函数图象上,满足△ACD的面积等于△ABC的面积,求直线BD的解析式.
【解答】解:(1)如图,设AB与x轴交于点E.
∵B是点A关于x轴的对称点,△ABO的面积是4,
∴S△AOE=2.
∴,即AE EO=4.
又AE EO=k.
∴k=4.
∴反比例函数的解析式.
(2)∵点A的横坐标为1,
当x=1时,y=4,
∴A(1,4).
由点A与点B关于x轴对称得B(1,﹣4).
由题可得,点A与点C关于原点O对称,
∴C(﹣1,﹣4),
过B点作BD∥AC,直线BD与反比例函数在第一象限的图象的交点为所求点D,
∴S△ADC=S△ABC.
设直线AC的解析式为y=ax(a≠0).
将A(1,4)代入上式,得a=4,
∴直线AC解析式为y=4x.
∵AC∥BD,
∴可设直线BD的解析式为y=4x+b,
将B(1,﹣4)代入上式,得到﹣4=4+b,
解得b=﹣8.
∴直线BD的解析式为y=4x﹣8.
24.(2023秋 淮阳区校级期末)某校第二课堂准备设置球类课程,随机抽取部分学生进行问卷调查,被调查学生须从“羽毛球”“篮球”“足球”“排球”“乒乓球”中选择自己最喜欢的一项.根据调查结果绘制了不完整的条形统计图和扇形统计图,请根据图中信息,解答下列问题:
(1)此次共调查了 200 名学生;
(2)将条形统计图补充完整;
(3)该校把最受欢迎的“羽毛球”“篮球”“足球”设置为选修内容.小明和小亮分别从三个项目中任选一项进行训练,利用树状图或表格求出他俩选择同一项目的概率.
【解答】解:(1)此次共调查的学生有:(名);
(2)足球的人数有:200﹣40﹣60﹣20﹣30=50(名),补全统计图如图1:
(3)设“羽毛球”“篮球”“足球”分别为A、B、C,根据题意画树状图如图2:
共有9种等可能的情况,其中他俩选择相同项目的有3种,
则P(他俩选择相同项目).
25.(2023秋 益阳期末)如图,一次函数y1=ax+b的图象与反比例函数的图象相交于A(n,3)和B(3,﹣1)两点,一次函数y1=ax+b图象分别与x轴,y轴交于E,D两点,过A作AC⊥x轴,垂足为C,连接OB.
(1)求一次函数解析式和反比例函数解析式.
(2)点P为反比例函数图象上一点,若S△BOD=S△PCE,求点P的坐标.
(3)直接写出不等式的解集.
【解答】解:(1)将点B(3,﹣1)代入,得:k=3×(﹣1)=﹣3,
则反比例函数解析式为y,
∵反比例函数的图象过A(n,3),
∴3,
∴n=﹣1,
∴A(﹣1,3),
将点A(﹣1,3)、B(3,﹣1)代入y=ax+b得,
解得,
则一次函数解析式为y=﹣x+2;
(2)令x=0,则y=﹣x+2=2,
∴D(0,2),
令y=0,则﹣x+2=0,解得x=2,
∴E(2,0),
∴S△BOD3,
∵AC⊥x轴,垂足为C,
∴C(﹣1,0),
∴CE=3,
∵S△BOD=S△PCE,
∴,
∴,
∴yP=±2,
把y=2代入y得到,x,
把y=﹣2代入y得到,x,
∴点P的坐标为(,2)或(,﹣2).
(3)∵一次函数y1=ax+b的图象与反比例函数的图象相交于A(﹣1,3)和B(3,﹣1)两点,
由图象可得,﹣1<x<0或x>3时,ax+b.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
