2016年山东省枣庄市第39中学中考数学二模拟试卷(无答案)
文档属性
| 名称 | 2016年山东省枣庄市第39中学中考数学二模拟试卷(无答案) |
|
|
| 格式 | zip | ||
| 文件大小 | 96.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-04-24 00:00:00 | ||
图片预览

文档简介
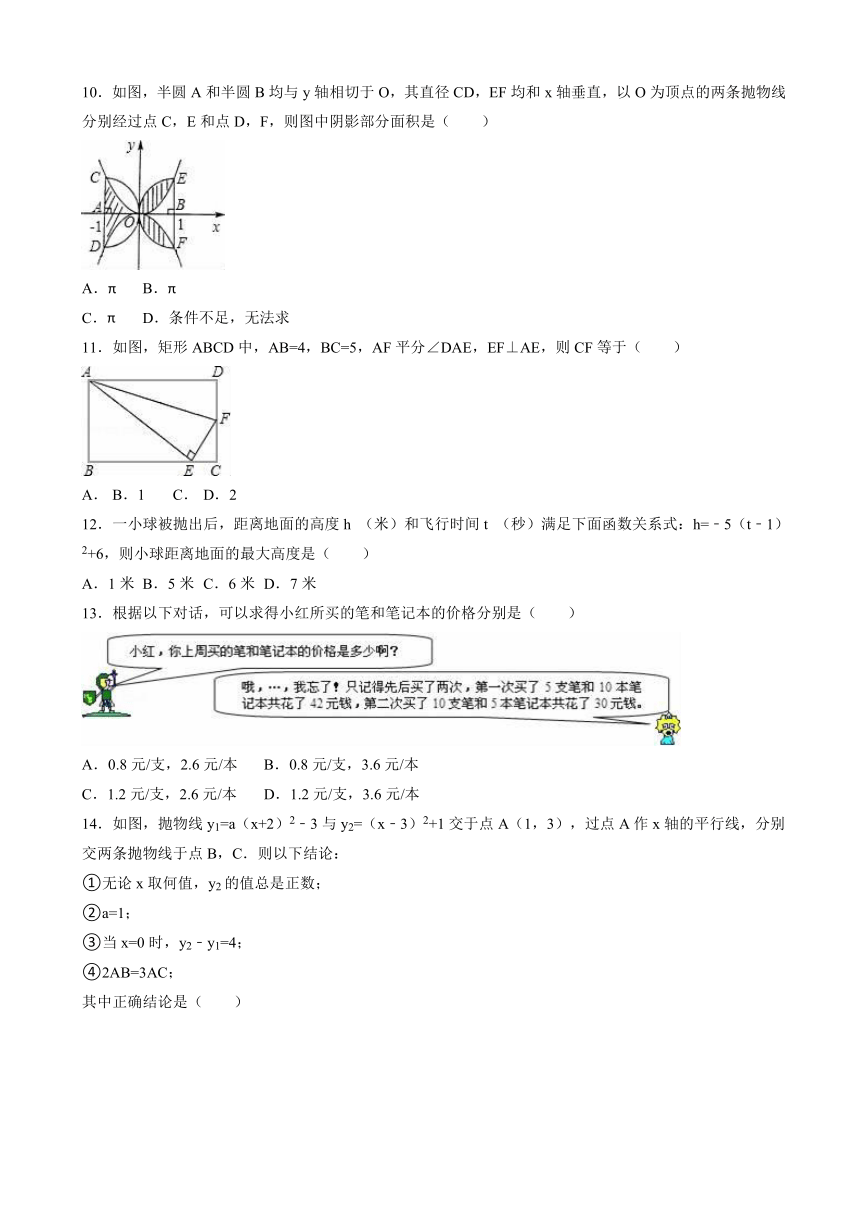
2016年山东省枣庄市第39中学中考数学模拟试卷
一、选择题(本题有14个小题,每小题3分,共42分)
1.﹣2的倒数是( )
A.﹣2 B.﹣ C. D.2
2.某种生物细胞的直径约为0.00056m,将0.00056用科学记数法表示为( )
A.0.56×10﹣3 B.5.6×10﹣4 C.5.6×10﹣5 D.56×10﹣5
3.如图,摆放的几何体的俯视图是( )
A. B. C. D.
4.设a>0,b>0,则下列运算错误的是( )
A. = B. =+ C.()2=a D. =
5.抛物线y=x2向右平移2个单位,再向上平移3个单位,得到的抛物线的解析式为( )
A.y=(x+2)2+3 B.y=(x﹣2)2+3 C.y=(x﹣2)2﹣3 D.y=(x+2)2﹣3
6.下列四个图形中,既是轴对称图形,又是中心对称图形的是( )
A.①② B.①③ C.②③ D.①②③
7.一条葡萄藤上结有五串葡萄,每串葡萄的粒数如图所示(单位:粒).则这组数据的中位数为( )
A.37 B.35 C.33.8 D.32
8.不等式组的解集为( )
A.x>﹣2 B.﹣2<x<2 C.x≤2 D.﹣2<x≤2
9.在同一平面直角坐标系内,一次函数y=ax+b与二次函数y=ax2+5x+b的图象可能是( )
A. B. C. D.
10.如图,半圆A和半圆B均与y轴相切于O,其直径CD,EF均和x轴垂直,以O为顶点的两条抛物线分别经过点C,E和点D,F,则图中阴影部分面积是( )
A.π B.π
C.π D.条件不足,无法求
11.如图,矩形ABCD中,AB=4,BC=5,AF平分∠DAE,EF⊥AE,则CF等于( )
A. B.1 C. D.2
12.一小球被抛出后,距离地面的高度h (米)和飞行时间t (秒)满足下面函数关系式:h=﹣5(t﹣1)2+6,则小球距离地面的最大高度是( )
A.1米 B.5米 C.6米 D.7米
13.根据以下对话,可以求得小红所买的笔和笔记本的价格分别是( )
A.0.8元/支,2.6元/本 B.0.8元/支,3.6元/本
C.1.2元/支,2.6元/本 D.1.2元/支,3.6元/本
14.如图,抛物线y1=a(x+2)2﹣3与y2=(x﹣3)2+1交于点A(1,3),过点A作x轴的平行线,分别交两条抛物线于点B,C.则以下结论:
①无论x取何值,y2的值总是正数;
②a=1;
③当x=0时,y2﹣y1=4;
④2AB=3AC;
其中正确结论是( )
二、填空题:(本大题共4个小题,每小题4分,共16分)
15.分解因式:ax+ay= .
16.某家用电器经过两次降价,每台零售价由350元下降到299元.若两次降价的百分率相同,设这个百分率为x,则可列出关于x的方程为 .
17.如图,⊙O的半径OD⊥弦AB于点C,连结AO并延长交⊙O于点E,连结EC.若AB=8,CD=2,则EC的长为 .
17.一个不透明的袋子中有2个红球、3个黄球和4个蓝球,这些球除颜色外完全相同,从袋子中随机摸出一个球,它是红色球的概率为 .
18.如图,等腰直角三角形ABC的直角边AB的长为6cm,将△ABC绕点A逆时针旋转15°后得到△AB′C′,则图中阴影部分面积等于 cm2.
三、解答题:(本大题共62分)解答时每小题必须给出必要的演算过程或推理步骤.
19.(1)计算:﹣2sin30° tan45°
(2)解不等式组:.
20.“端午节”是我国的传统佳节,民间历来有吃“粽子”的习俗,我市某食品厂为了解市民对去年销售量较好的肉馅粽、豆沙粽、红枣粽、蛋黄馅粽(以下分别用A、B、C、D表示这四种不同口味粽子的喜爱情况,在节前对某居民区市民进行了抽样调查,并将调查结果绘制成如下两幅统计图.请根据以上信息回答:
(1)本次参加抽样调查的居民有多少人?
(2)将不完整的条形图补充完整.
(3)若居民区有8000人,请估计爱吃D粽的人数?
21.为缓解“停车难”的问题,某单位拟建造地下停车库,建筑设计师提供了该地下停车库的设计示意图,按规定,地下停车库坡道口上方要张贴限高标志,以便告知停车人车辆能否安全驶入,为标明限高,请你根据该图计算CE.
(sin18°≈0.3090,cos18°≈0.9511,tan18°≈0.3249)(精确到0.1m)
22.列方程和方程组解应用题:
某班有40名同学去看演出,购买甲、乙两种票共用去370元,其中甲种票每张10元,乙种票每张8元,求购买了甲、乙两种票各多少张?
23.如图,在边长为2的正方形ABCD中,P为AB的中点,Q为边CD上一动点,设DQ=t(0≤t≤2),线段PQ的垂直平分线分别交边AD、BC于点M、N,过Q作QE⊥AB于点E,过M作MF⊥BC于点F.
(1)当t≠1时,求证:△PEQ≌△NFM;
(2)顺次连接P、M、Q、N,设四边形PMQN的面积为S,求出S与自变量t之间的函数关系式,并求S的最小值.
24.如图,抛物线y=ax2+bx经过点A(﹣4,0)、B(﹣2,2),连接OB、AB,
(1)求该抛物线的解析式.
(2)求证:△OAB是等腰直角三角形.
(3)将△OAB绕点O按逆时针方向旋转135°,得到△OA′B′,写出A′B′的中点P的坐标,试判断点P是否在此抛物线上.
(4)在抛物线上是否存在这样的点M,使得四边形ABOM成直角梯形?若存在,请求出点M坐标及该直角梯形的面积;若不存在,请说明理由.
一、选择题(本题有14个小题,每小题3分,共42分)
1.﹣2的倒数是( )
A.﹣2 B.﹣ C. D.2
2.某种生物细胞的直径约为0.00056m,将0.00056用科学记数法表示为( )
A.0.56×10﹣3 B.5.6×10﹣4 C.5.6×10﹣5 D.56×10﹣5
3.如图,摆放的几何体的俯视图是( )
A. B. C. D.
4.设a>0,b>0,则下列运算错误的是( )
A. = B. =+ C.()2=a D. =
5.抛物线y=x2向右平移2个单位,再向上平移3个单位,得到的抛物线的解析式为( )
A.y=(x+2)2+3 B.y=(x﹣2)2+3 C.y=(x﹣2)2﹣3 D.y=(x+2)2﹣3
6.下列四个图形中,既是轴对称图形,又是中心对称图形的是( )
A.①② B.①③ C.②③ D.①②③
7.一条葡萄藤上结有五串葡萄,每串葡萄的粒数如图所示(单位:粒).则这组数据的中位数为( )
A.37 B.35 C.33.8 D.32
8.不等式组的解集为( )
A.x>﹣2 B.﹣2<x<2 C.x≤2 D.﹣2<x≤2
9.在同一平面直角坐标系内,一次函数y=ax+b与二次函数y=ax2+5x+b的图象可能是( )
A. B. C. D.
10.如图,半圆A和半圆B均与y轴相切于O,其直径CD,EF均和x轴垂直,以O为顶点的两条抛物线分别经过点C,E和点D,F,则图中阴影部分面积是( )
A.π B.π
C.π D.条件不足,无法求
11.如图,矩形ABCD中,AB=4,BC=5,AF平分∠DAE,EF⊥AE,则CF等于( )
A. B.1 C. D.2
12.一小球被抛出后,距离地面的高度h (米)和飞行时间t (秒)满足下面函数关系式:h=﹣5(t﹣1)2+6,则小球距离地面的最大高度是( )
A.1米 B.5米 C.6米 D.7米
13.根据以下对话,可以求得小红所买的笔和笔记本的价格分别是( )
A.0.8元/支,2.6元/本 B.0.8元/支,3.6元/本
C.1.2元/支,2.6元/本 D.1.2元/支,3.6元/本
14.如图,抛物线y1=a(x+2)2﹣3与y2=(x﹣3)2+1交于点A(1,3),过点A作x轴的平行线,分别交两条抛物线于点B,C.则以下结论:
①无论x取何值,y2的值总是正数;
②a=1;
③当x=0时,y2﹣y1=4;
④2AB=3AC;
其中正确结论是( )
二、填空题:(本大题共4个小题,每小题4分,共16分)
15.分解因式:ax+ay= .
16.某家用电器经过两次降价,每台零售价由350元下降到299元.若两次降价的百分率相同,设这个百分率为x,则可列出关于x的方程为 .
17.如图,⊙O的半径OD⊥弦AB于点C,连结AO并延长交⊙O于点E,连结EC.若AB=8,CD=2,则EC的长为 .
17.一个不透明的袋子中有2个红球、3个黄球和4个蓝球,这些球除颜色外完全相同,从袋子中随机摸出一个球,它是红色球的概率为 .
18.如图,等腰直角三角形ABC的直角边AB的长为6cm,将△ABC绕点A逆时针旋转15°后得到△AB′C′,则图中阴影部分面积等于 cm2.
三、解答题:(本大题共62分)解答时每小题必须给出必要的演算过程或推理步骤.
19.(1)计算:﹣2sin30° tan45°
(2)解不等式组:.
20.“端午节”是我国的传统佳节,民间历来有吃“粽子”的习俗,我市某食品厂为了解市民对去年销售量较好的肉馅粽、豆沙粽、红枣粽、蛋黄馅粽(以下分别用A、B、C、D表示这四种不同口味粽子的喜爱情况,在节前对某居民区市民进行了抽样调查,并将调查结果绘制成如下两幅统计图.请根据以上信息回答:
(1)本次参加抽样调查的居民有多少人?
(2)将不完整的条形图补充完整.
(3)若居民区有8000人,请估计爱吃D粽的人数?
21.为缓解“停车难”的问题,某单位拟建造地下停车库,建筑设计师提供了该地下停车库的设计示意图,按规定,地下停车库坡道口上方要张贴限高标志,以便告知停车人车辆能否安全驶入,为标明限高,请你根据该图计算CE.
(sin18°≈0.3090,cos18°≈0.9511,tan18°≈0.3249)(精确到0.1m)
22.列方程和方程组解应用题:
某班有40名同学去看演出,购买甲、乙两种票共用去370元,其中甲种票每张10元,乙种票每张8元,求购买了甲、乙两种票各多少张?
23.如图,在边长为2的正方形ABCD中,P为AB的中点,Q为边CD上一动点,设DQ=t(0≤t≤2),线段PQ的垂直平分线分别交边AD、BC于点M、N,过Q作QE⊥AB于点E,过M作MF⊥BC于点F.
(1)当t≠1时,求证:△PEQ≌△NFM;
(2)顺次连接P、M、Q、N,设四边形PMQN的面积为S,求出S与自变量t之间的函数关系式,并求S的最小值.
24.如图,抛物线y=ax2+bx经过点A(﹣4,0)、B(﹣2,2),连接OB、AB,
(1)求该抛物线的解析式.
(2)求证:△OAB是等腰直角三角形.
(3)将△OAB绕点O按逆时针方向旋转135°,得到△OA′B′,写出A′B′的中点P的坐标,试判断点P是否在此抛物线上.
(4)在抛物线上是否存在这样的点M,使得四边形ABOM成直角梯形?若存在,请求出点M坐标及该直角梯形的面积;若不存在,请说明理由.
同课章节目录
