2024-2025学年五年级数学上册寒假巩固练习(人教版)第6练-多边形的面积(含答案+解析)
文档属性
| 名称 | 2024-2025学年五年级数学上册寒假巩固练习(人教版)第6练-多边形的面积(含答案+解析) |
|
|
| 格式 | docx | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-01-24 00:00:00 | ||
图片预览

文档简介
2024-2025学年五年级数学上册寒假巩固练习(人教版)
第6练-多边形的面积
一、认真审题,精确计算(共14分)
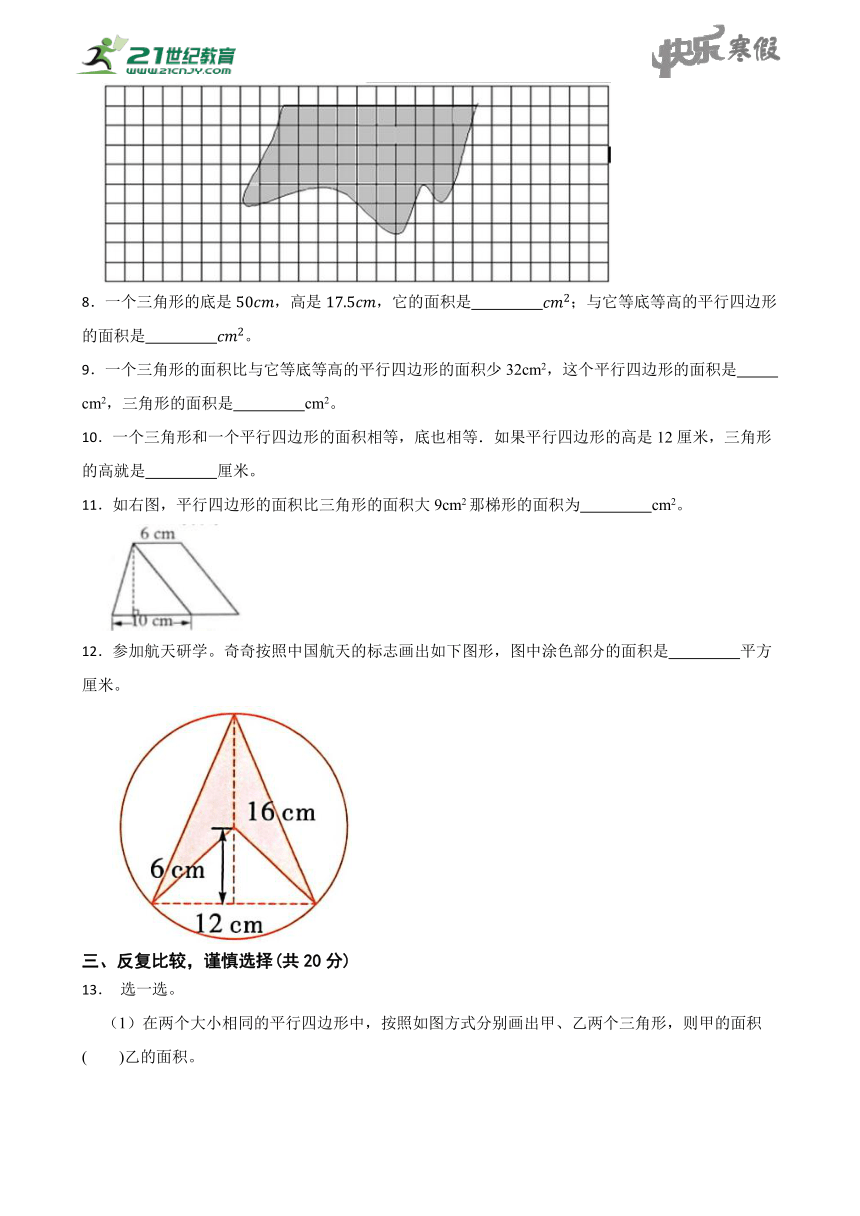
1.求下列组合图形的面积。(单位:厘米)
2.下图是由大、小两个正方形组成,大正方形面积为16,小正方形面积为9,求阴影部分的面积。
二、用心思考,正确填空(共20分)
3.电动伸缩门的设计运用了平行四边形的 。
4.一个三角形的面积是36平方厘米,与它等底等高的平行四边形的面积是 平方厘米,如果平行四边形底是9厘米,那么高是 厘米。
5.如图所示,BC为30厘米,直角梯形 ABCD的面积是 cm2
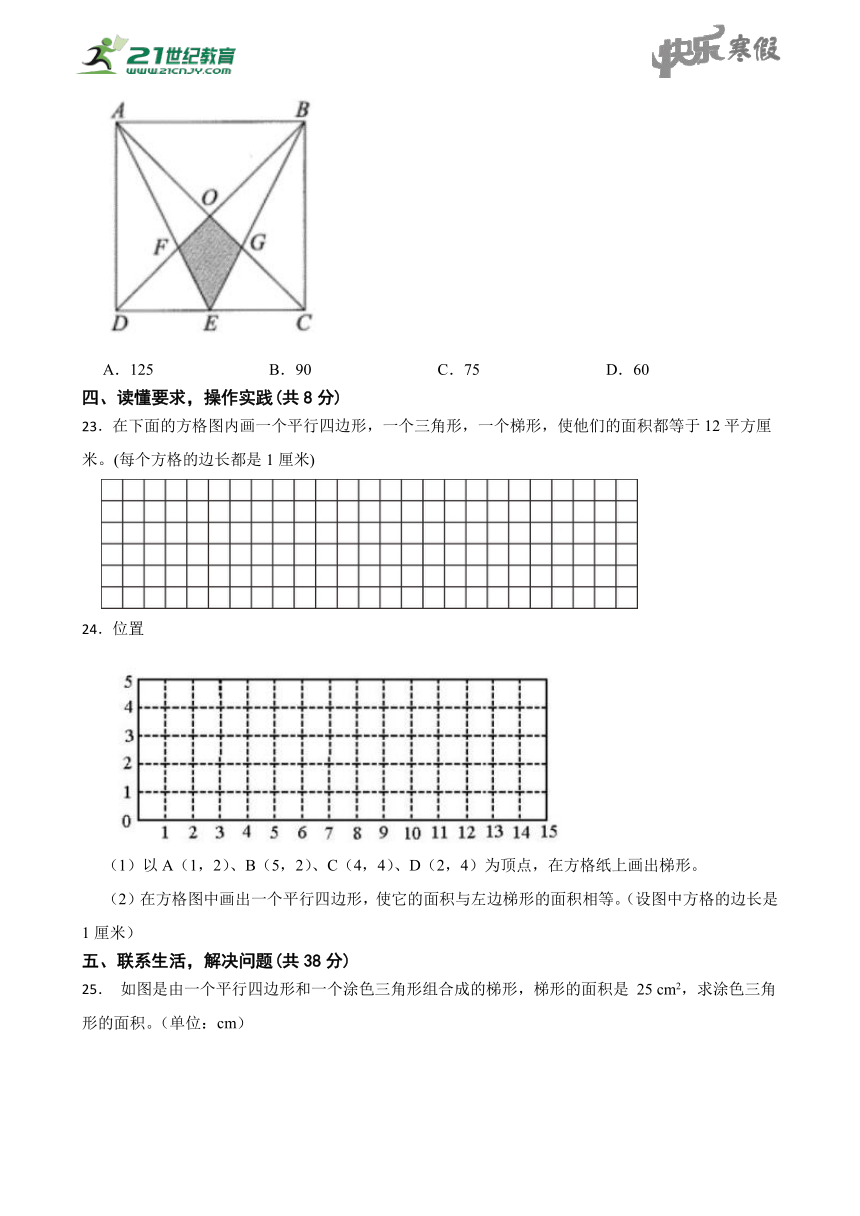
6. 一个三角形与一个平行四边形面积相等,高也相等。已知平行四边形底是2.4厘米,那么三角形的底是 厘米。
7.如果图中每个小正方形的格子面积为1平方厘米,那么阴影部分图形的面积大约是 平方厘米.
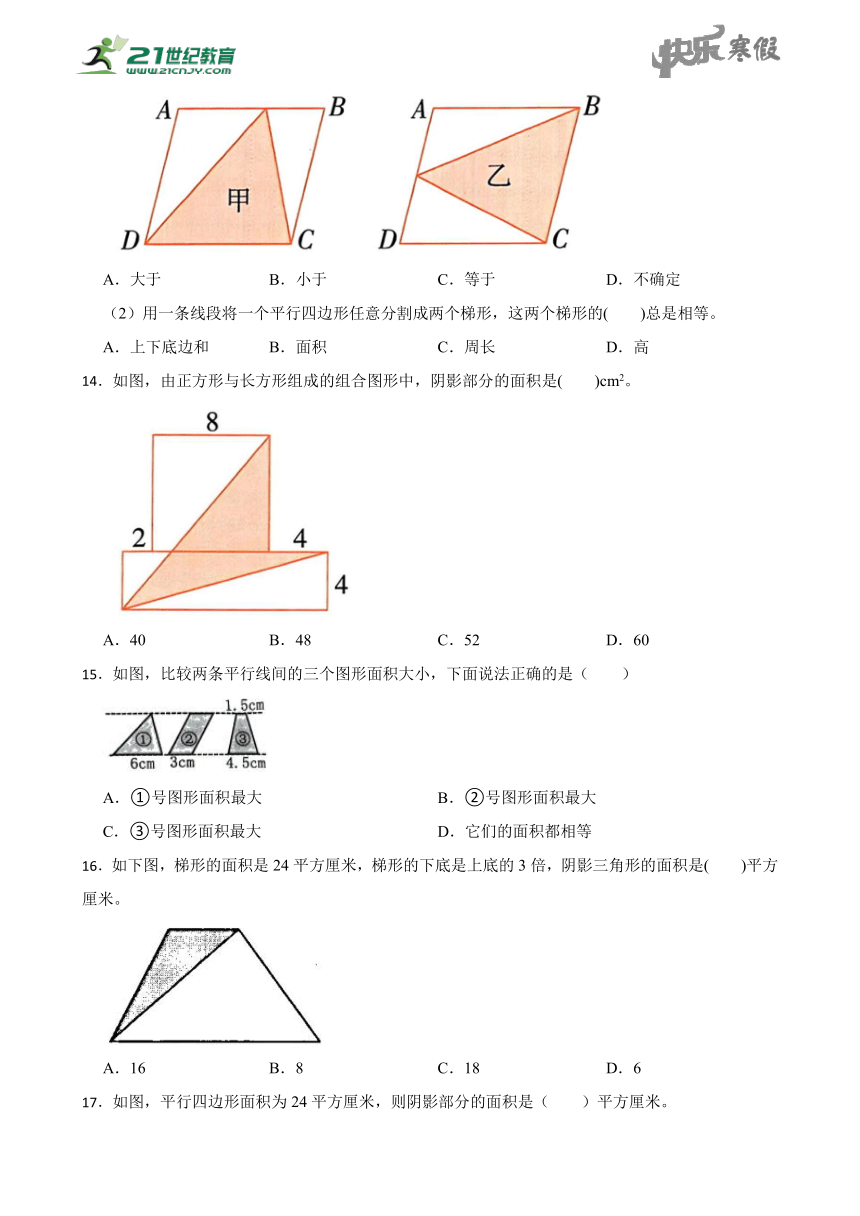
8.一个三角形的底是,高是,它的面积是 ;与它等底等高的平行四边形的面积是 。
9.一个三角形的面积比与它等底等高的平行四边形的面积少32cm2,这个平行四边形的面积是 cm2,三角形的面积是 cm2。
10.一个三角形和一个平行四边形的面积相等,底也相等.如果平行四边形的高是12厘米,三角形的高就是 厘米。
11.如右图,平行四边形的面积比三角形的面积大9cm2那梯形的面积为 cm2。
12.参加航天研学。奇奇按照中国航天的标志画出如下图形,图中涂色部分的面积是 平方厘米。
三、反复比较,谨慎选择(共20分)
13. 选一选。
(1)在两个大小相同的平行四边形中,按照如图方式分别画出甲、乙两个三角形,则甲的面积( )乙的面积。
A.大于 B.小于 C.等于 D.不确定
(2)用一条线段将一个平行四边形任意分割成两个梯形,这两个梯形的( )总是相等。
A.上下底边和 B.面积 C.周长 D.高
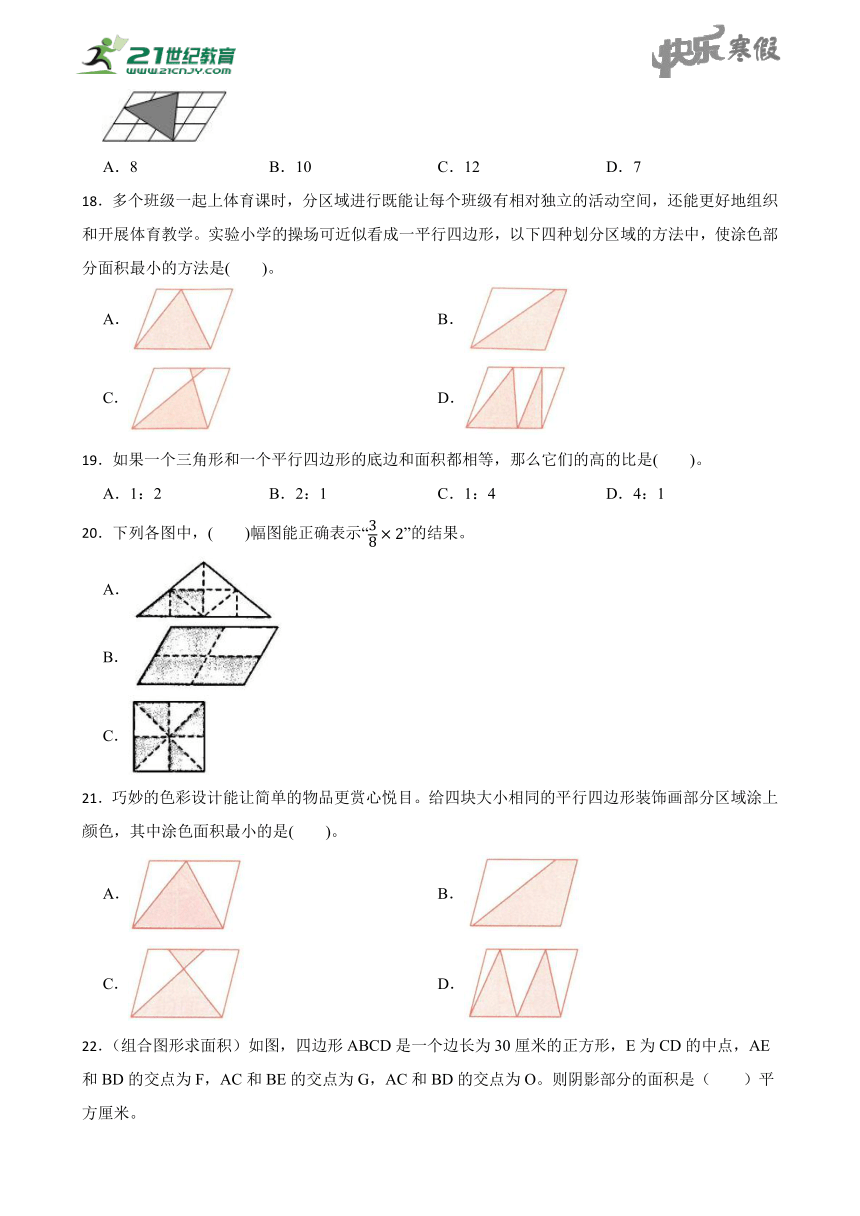
14.如图,由正方形与长方形组成的组合图形中,阴影部分的面积是( )cm2。
A.40 B.48 C.52 D.60
15.如图,比较两条平行线间的三个图形面积大小,下面说法正确的是( )
A.①号图形面积最大 B.②号图形面积最大
C.③号图形面积最大 D.它们的面积都相等
16.如下图,梯形的面积是24平方厘米,梯形的下底是上底的3倍,阴影三角形的面积是( )平方厘米。
A.16 B.8 C.18 D.6
17.如图,平行四边形面积为24平方厘米,则阴影部分的面积是( )平方厘米。
A.8 B.10 C.12 D.7
18.多个班级一起上体育课时,分区域进行既能让每个班级有相对独立的活动空间,还能更好地组织和开展体育教学。实验小学的操场可近似看成一平行四边形,以下四种划分区域的方法中,使涂色部分面积最小的方法是( )。
A. B.
C. D.
19.如果一个三角形和一个平行四边形的底边和面积都相等,那么它们的高的比是( )。
A.1:2 B.2:1 C.1:4 D.4:1
20.下列各图中,( )幅图能正确表示“”的结果。
A.
B.
C.
21.巧妙的色彩设计能让简单的物品更赏心悦目。给四块大小相同的平行四边形装饰画部分区域涂上颜色,其中涂色面积最小的是( )。
A. B.
C. D.
22.(组合图形求面积)如图,四边形ABCD是一个边长为30厘米的正方形,E为CD的中点,AE和BD的交点为F,AC和BE的交点为G,AC和BD的交点为O。则阴影部分的面积是( )平方厘米。
A.125 B.90 C.75 D.60
四、读懂要求,操作实践(共8分)
23.在下面的方格图内画一个平行四边形,一个三角形,一个梯形,使他们的面积都等于12平方厘米。(每个方格的边长都是1厘米)
24.位置
(1)以A(1,2)、B(5,2)、C(4,4)、D(2,4)为顶点,在方格纸上画出梯形。
(2)在方格图中画出一个平行四边形,使它的面积与左边梯形的面积相等。(设图中方格的边长是1厘米)
五、联系生活,解决问题(共38分)
25. 如图是由一个平行四边形和一个涂色三角形组合成的梯形,梯形的面积是 25 cm2,求涂色三角形的面积。(单位:cm)
26.闸门起重机是三峡大坝上一道靓丽的风景,起重机的一个桥架是由五根钢材搭成的,且呈梯形状(如图),已知梯形ABCD的面积是240m2,AE=BF=36.5m,若每米钢材的成本是320元,制作一个桥架需要多少钱
27. 新情境 地域特色 我国是最早发现并利用茶的国家,六(lù)安瓜片茶更是有悠久的历史,据《六安州志》记载:“茶之极品,明朝始入贡。”说明六安瓜片茶在明朝就已经很出名了。现有一块底为2千米,高为600米的三角形茶园,这块茶园的面积为多少公顷?若每公顷产茶叶1600 千克,这块茶园可产茶叶多少吨?
28.对于一些重要考古遗迹通常会采用建立遗址博物馆的形式进行原址保护。某地将一处长方形遗址宽度增加50米以便建设配套设施维护、管理与开发,现在遗址区域变成了正方形,面积增加了1公顷,原遗址面积为多少公顷?
29.计算每个图形的面积。
图形 平行四边形 三角形 梯形
底/cm 0.9 12 上底8下底12
高/cm 0.4 5 15
面积/cm2
图形 平行四边形 三角形 梯形
底/cm 0.9 12 上底8下底12
高/cm 0.4 5 15
面积/cm2
答案解析部分
1.解:第一个图:
(平方厘米)
(平方厘米)
(平方厘米)
第二个图:
(平方厘米)
(平方厘米)
(平方厘米)
第一个图:组合图形的面积=长方形的面积-三角形的面积,其中,长方形的面积=长×宽,三角形的面积=底×高÷2;
第二个图:组合图形的面积=平行四边形的面积+直角三角形的面积;其中,平行四边形的面积=底×高,三角形面积=底×高÷2。
2.解:如图,连接BD
因为4×4=16,所以,大正方形的边长是4
因为3×3=9,所以,小正方形的边长是3
所以,S阴影=S△ABD+S△DBC+S△ABC =
=2+4.5+1.5
=8
答: 阴影部分的面积为8
如图,连接BD
阴影部分面积等于三角形ABC的面积加上三角形ABD的面积加上三角形CBD的面积,通过题干信息进行运算即可求解
3.容易变形
解:电动伸缩门的设计运用了平行四边形的容易变形的特性。
故答案为:容易变形。
平行四边形具有不稳定性、容易变形,这种特性在生活中的具有广泛的应用:伸缩衣架、小区门口的电动门、小商店门口的推拉门、折叠椅子等。
4.72;8
解:36×2=72(平方厘米)
72÷9=8(厘米)
故答案为:72;8。
等底等高的平行四边形的面积是三角形面积的2倍;平行四边形面积÷平行四边形底=平行四边形高。
5.450
解:如图:
根据三角形的内角和是180°和等腰直角三角形的性质可知,
AB=BE,CD=CE,AB+CD=BE+EC=30(厘米)
直角梯形 ABCD的面积:
(AB+CD)×BC÷2=30×30÷2=450(平方厘米)
故答案为:450。
梯形的面积=(上底+下底)×高÷2。
6.4.8
解:2.4×2=4.8(厘米)。
故答案为:4.8。
等底等高的平行四边形的面积是三角形面积的2倍,所以这个三角形的底=平行四边形的底×2。
7.50
解:10×5=50(平方厘米)。
故答案为:50。
阴影部分图形可以看作一个近似的底10厘米,高5厘米的平行四边形,面积=底×高。
8.437.5;875
解:50×17.5÷2=437.5(cm2),所以这个三角形的面积是437.5cm2;437.5×2=875(cm2),所以与它等底等高的平行四边形的面积是875cm2。
故答案为:437.5;875。
三角形的面积=底×高÷2;
等底等高三角形的面积是平行四边形面积的一半。
9.64;32
解:32÷(2-1)
=32÷1
=32(平方分米)
32×2=64(平方分米)
平行四边形面积是64平方分米,三角形面积是32平方分米。
故答案为:64;32。
根据等底等高的平行四边形面积是三角形的2倍,把三角形的面积看作1份,平行四边形的面积是2份,则相差(2-1)份,由此求出一份,进而求出平行四边形的面积。
10.24
解:12×2=24(厘米)。
故答案为:24。
等底等高的平行四边形的面积是三角形面积的2倍,三角形的高=平行四边形的高×2。
11.99
解:6×高-10×高÷2=9
6×高-5×高=9
高=9
(10+6+6)×9÷2=22×9÷2=99(平方厘米)
故答案为:99。
等量关系:平行四边形的面积-三角形的面积=9,据此求出他们的高;梯形的面积=(上底+下底)×高÷2,据此解答。
12.60
解:12×16÷2-12×6÷2
=96-36
=60(平方厘米)
故答案为:60。
观察图形,涂色部分面积等于大三角形面积减去小空白三角形的面积,根据三角形面积公式S=底×高÷2计算。
13.(1)C
(2)D
解:(1)连接BD,甲、乙两个三角形均和三角形BCD等底等高,所以甲、乙两个三角形均和三角形BCD的面积相同,则甲的面积等于乙的面积。
(2)根据两平行线之间的距离相等,可知,把一个平行四边形任意分割成两个梯形,这两个梯形的高一定相等
故答案为:C;D
(1)根据等高同底的性质和三角形的面积公式:S=底×高÷2即可判断
(2)根据两平行线之间的距离相等,据此即可解答。
14.B
解:将正方形右下角与长方形左下角相连接,
大三角形:8×(2+8)÷2=40(cm2)
小三角形:阴影部分:40+8=48(cm2)
做出辅助线后,可以看出阴影部分面积为两个三角形的面积之和。分别计算两个三角形的面积,两者相加即可。
15.D
解:假设高都是h厘米,
①6h÷2=3h;
②3h;
③(1.5+4.5)h÷2=3h;
所以它们的面积都相等。
故答案为:D。
三角形面积=底×高÷2,平行四边形面积=底×高,梯形面积=(上底+下底)×高÷2,假设它们的高都是h厘米;分别计算出面积,再比较面积的大小即可。
16.D
解:24÷(1+3)
=24÷4
=6(平方厘米)
故答案为:D。
根据图可知,阴影部分面积加上空白部分面积就是梯形的面积,由于两个三角形的高都是梯形的高,空白部分三角形的底是阴影部分三角形底的3倍,则阴影部分三角形的面积=梯形面积÷(1+3),代入数值计算即可解答。
17.D
解:
24÷12=2(平方厘米)
平行四边形ABCD的面积:2×9=18(平方厘米)
空白三角形①的面积:
2×6÷2
=12÷2
=6(平方厘米)
空白三角形②的面积:
2×3÷2
=6÷2
=3(平方厘米)
空白三角形③的面积:
2×2÷2
=4÷2
=2(平方厘米)
阴影部分的面积:
18-(6+3+2)
=18-11
=7(平方厘米)。
故答案为:D。
大平行四边形又被平均分成了12个小平行四边形,平均每个小平行四边形的面积是24÷12=2平方厘米,分别计算出①、②、③空白三角形的面积;阴影部分的面积=平行四边形ABCD的面积-三个空白三角形的面积和。
18.C
解:A和D的涂色部分的面积均占平行四边形面积的一半,B涂色部分的面积比平行四边形面积的一半多一些,C涂色部分的面积比平行四边形面积的一半少一些,所以C的涂色部分的面积最小。
故答案为:C。
根据等底等高判断出A和D的面积是平行四边形面积的一半;再去判断B和C涂色面积与平行四边形一半面积的关系。
19.B
解:平行四边形的面积是:S=ah1,
三角形的面积是:S=ah2÷2,
所以ah1=ah2÷2,
h1=h2÷2,
即:h2=2h1
所以h2:h1=2:1
故答案为:B。
根据平行四边形的面积公式S=ah及三角形的面积公式S=ah÷2,推导出在一个平行四边形和一个三角形的面积相等,底边长相等时,高的关系即可。
20.B
解:
A:阴影部分面积:,所以,A错误
B:阴影部分面积:,所以,B正确
C:阴影部分面积:,所以,C错误
故答案为:B
(1)利用阴影部分三角形的个数除以大三角中小三角的总个数,然后计算出阴影部分面积占大三角形比例即可
(2)根据阴影小平行四边形的个数除以大平行四边形中小平行四边形的总个数,然后计算出阴影部分面积占三角形比例即可
(3)利用阴影部分三角形的个数除以正方形中小三角的总个数,然后计算出阴影部分面积占正方形比例即可
21.C
解:A和D的涂色面积均占平行四边形面积的一半,B比平行四边形面积的一半多一些,C比平行四边形面积的一半少一些,所以C涂色面积最小。
故答案为:C。
根据涂颜色的形状,以及与平行四边形的面积大小关系进行比较得出结论。
22.C
连接OE,四边形ABCD 是一个边长是30厘米的正方形,E是CD的中点。
正方形ABCD ═ ×30×30 = 112.5(平方厘米)
BO=DO,CE=DE,OE是△BCD的中位线。
从而
(平方厘米)
同理可得 : (平方厘米)
(平方厘米)
故答案为:C。
因为E是正方形边的中点,所以可得△ADE的面积等于正方形面积的四分之一,△AFB∽△EDF,则DE:AB=EF:FA=1:2,可以得到△EDF的面积=×△ADE的面积=×正方形面积=×正方形面积。同理可证,△CEG的面积=×正方形面积。进而求出阴影部分的面积即可。
23.解:平行四边形的底画4格,高画3格,平行四边形面积=4×3=12(平方厘米)
三角形的底画8格,高画3格,平行四边形面积=8×3÷2=12(平方厘米)
梯形的上底画3格,下底画5格,高画3格,梯形面积=(3+5)×3÷2=12(平方厘米)
平行四边形面积=底×高,三角形面积=底×高÷2,梯形面积=(上底+下底)×高÷2,据此作图。
24.(1)解:
(2)解:(2+4)×2÷2
=6×2÷2
=12÷2
=6(平方厘米)
2×3=6(平方厘米)
(1)用数对表示位置时,前面一个数表示第几列,后面一个数表示第几行;列数一般从左往右数,行数一般从前往后数,顺次连接各点画出梯形;
(2)梯形的面积=(上底+下底)×高÷2,平行四边形的面积=底×高,依据梯形的面积计算出平行四边形底与高的格数,从而画出平行四边形。
25.25×2÷(3+7)=5( cm)
(7-3)×5÷2=10(cm2)
26.解:根据题意,可得
AB和DC的长度和:240×2÷12=40(m),
五条钢材的长度和:40+25+36.5×2=138(m),
138×320=44160(元)。
答:制作一个桥架需要44160元。
观察图形,根据梯形的面积公式:S=(上底+下底)×高÷2,可知,上底+下底=2S÷高,代入数据求出AB+DC的长度和;然后再求出五条钢材的长度和:40+25+36.5×2,最后再乘以每米钢材的成本价,即可求出总价钱。
27.解:2千米=2000米,
茶园的面积为2000×600÷2=600000(平方米)。
600000平方米=60公顷,
60×1600=96000(千克),
96000千克=96吨。
答:这块茶园的面积为60公顷,可产茶叶96吨。
根据1千米=1000米,1公顷=10000平方米,1吨=10000千克进行单位的换算;根据三角形面积=底×高÷2求出茶园的面积,再根据每公顷产茶叶1600千克求出茶园一共可产茶叶多少吨。
28.解:1公顷=10000平方米。
原遗址长:10000÷50=200(米),
原遗址面积:200×(200-50)=30000(平方米),
30000平方米=3公顷,
答:原遗址面积为3公顷。
首先将公顷换算成平方米,其中1公顷=10000平方米;增加后的遗址是一个正方形,用增加的面积除以增加的宽度得到原遗址的长度,用原遗址长减去增加的长度得到原遗址的宽度,据此求出原遗址的面积,再将结果的单位换算成公顷。
29.解: 平行四边形面积:0.9×0.4=0.36(平方厘米),
三角形面积:12×5÷2=30(平方厘米),
梯形面积:
(8+12)×15÷2
=20×15÷2
=150(平方厘米)
图形 平行四边形 三角形 梯形
底/cm 0.9 12 上底8下底12
高/cm 0.4 5 15
面积/cm2 0.36 30 150
平行四边形面积=底×高,三角形面积=底×高÷2,梯形面积=(上底+下底)×高÷2,根据公式计算并填表即可。
第6练-多边形的面积
一、认真审题,精确计算(共14分)
1.求下列组合图形的面积。(单位:厘米)
2.下图是由大、小两个正方形组成,大正方形面积为16,小正方形面积为9,求阴影部分的面积。
二、用心思考,正确填空(共20分)
3.电动伸缩门的设计运用了平行四边形的 。
4.一个三角形的面积是36平方厘米,与它等底等高的平行四边形的面积是 平方厘米,如果平行四边形底是9厘米,那么高是 厘米。
5.如图所示,BC为30厘米,直角梯形 ABCD的面积是 cm2
6. 一个三角形与一个平行四边形面积相等,高也相等。已知平行四边形底是2.4厘米,那么三角形的底是 厘米。
7.如果图中每个小正方形的格子面积为1平方厘米,那么阴影部分图形的面积大约是 平方厘米.
8.一个三角形的底是,高是,它的面积是 ;与它等底等高的平行四边形的面积是 。
9.一个三角形的面积比与它等底等高的平行四边形的面积少32cm2,这个平行四边形的面积是 cm2,三角形的面积是 cm2。
10.一个三角形和一个平行四边形的面积相等,底也相等.如果平行四边形的高是12厘米,三角形的高就是 厘米。
11.如右图,平行四边形的面积比三角形的面积大9cm2那梯形的面积为 cm2。
12.参加航天研学。奇奇按照中国航天的标志画出如下图形,图中涂色部分的面积是 平方厘米。
三、反复比较,谨慎选择(共20分)
13. 选一选。
(1)在两个大小相同的平行四边形中,按照如图方式分别画出甲、乙两个三角形,则甲的面积( )乙的面积。
A.大于 B.小于 C.等于 D.不确定
(2)用一条线段将一个平行四边形任意分割成两个梯形,这两个梯形的( )总是相等。
A.上下底边和 B.面积 C.周长 D.高
14.如图,由正方形与长方形组成的组合图形中,阴影部分的面积是( )cm2。
A.40 B.48 C.52 D.60
15.如图,比较两条平行线间的三个图形面积大小,下面说法正确的是( )
A.①号图形面积最大 B.②号图形面积最大
C.③号图形面积最大 D.它们的面积都相等
16.如下图,梯形的面积是24平方厘米,梯形的下底是上底的3倍,阴影三角形的面积是( )平方厘米。
A.16 B.8 C.18 D.6
17.如图,平行四边形面积为24平方厘米,则阴影部分的面积是( )平方厘米。
A.8 B.10 C.12 D.7
18.多个班级一起上体育课时,分区域进行既能让每个班级有相对独立的活动空间,还能更好地组织和开展体育教学。实验小学的操场可近似看成一平行四边形,以下四种划分区域的方法中,使涂色部分面积最小的方法是( )。
A. B.
C. D.
19.如果一个三角形和一个平行四边形的底边和面积都相等,那么它们的高的比是( )。
A.1:2 B.2:1 C.1:4 D.4:1
20.下列各图中,( )幅图能正确表示“”的结果。
A.
B.
C.
21.巧妙的色彩设计能让简单的物品更赏心悦目。给四块大小相同的平行四边形装饰画部分区域涂上颜色,其中涂色面积最小的是( )。
A. B.
C. D.
22.(组合图形求面积)如图,四边形ABCD是一个边长为30厘米的正方形,E为CD的中点,AE和BD的交点为F,AC和BE的交点为G,AC和BD的交点为O。则阴影部分的面积是( )平方厘米。
A.125 B.90 C.75 D.60
四、读懂要求,操作实践(共8分)
23.在下面的方格图内画一个平行四边形,一个三角形,一个梯形,使他们的面积都等于12平方厘米。(每个方格的边长都是1厘米)
24.位置
(1)以A(1,2)、B(5,2)、C(4,4)、D(2,4)为顶点,在方格纸上画出梯形。
(2)在方格图中画出一个平行四边形,使它的面积与左边梯形的面积相等。(设图中方格的边长是1厘米)
五、联系生活,解决问题(共38分)
25. 如图是由一个平行四边形和一个涂色三角形组合成的梯形,梯形的面积是 25 cm2,求涂色三角形的面积。(单位:cm)
26.闸门起重机是三峡大坝上一道靓丽的风景,起重机的一个桥架是由五根钢材搭成的,且呈梯形状(如图),已知梯形ABCD的面积是240m2,AE=BF=36.5m,若每米钢材的成本是320元,制作一个桥架需要多少钱
27. 新情境 地域特色 我国是最早发现并利用茶的国家,六(lù)安瓜片茶更是有悠久的历史,据《六安州志》记载:“茶之极品,明朝始入贡。”说明六安瓜片茶在明朝就已经很出名了。现有一块底为2千米,高为600米的三角形茶园,这块茶园的面积为多少公顷?若每公顷产茶叶1600 千克,这块茶园可产茶叶多少吨?
28.对于一些重要考古遗迹通常会采用建立遗址博物馆的形式进行原址保护。某地将一处长方形遗址宽度增加50米以便建设配套设施维护、管理与开发,现在遗址区域变成了正方形,面积增加了1公顷,原遗址面积为多少公顷?
29.计算每个图形的面积。
图形 平行四边形 三角形 梯形
底/cm 0.9 12 上底8下底12
高/cm 0.4 5 15
面积/cm2
图形 平行四边形 三角形 梯形
底/cm 0.9 12 上底8下底12
高/cm 0.4 5 15
面积/cm2
答案解析部分
1.解:第一个图:
(平方厘米)
(平方厘米)
(平方厘米)
第二个图:
(平方厘米)
(平方厘米)
(平方厘米)
第一个图:组合图形的面积=长方形的面积-三角形的面积,其中,长方形的面积=长×宽,三角形的面积=底×高÷2;
第二个图:组合图形的面积=平行四边形的面积+直角三角形的面积;其中,平行四边形的面积=底×高,三角形面积=底×高÷2。
2.解:如图,连接BD
因为4×4=16,所以,大正方形的边长是4
因为3×3=9,所以,小正方形的边长是3
所以,S阴影=S△ABD+S△DBC+S△ABC =
=2+4.5+1.5
=8
答: 阴影部分的面积为8
如图,连接BD
阴影部分面积等于三角形ABC的面积加上三角形ABD的面积加上三角形CBD的面积,通过题干信息进行运算即可求解
3.容易变形
解:电动伸缩门的设计运用了平行四边形的容易变形的特性。
故答案为:容易变形。
平行四边形具有不稳定性、容易变形,这种特性在生活中的具有广泛的应用:伸缩衣架、小区门口的电动门、小商店门口的推拉门、折叠椅子等。
4.72;8
解:36×2=72(平方厘米)
72÷9=8(厘米)
故答案为:72;8。
等底等高的平行四边形的面积是三角形面积的2倍;平行四边形面积÷平行四边形底=平行四边形高。
5.450
解:如图:
根据三角形的内角和是180°和等腰直角三角形的性质可知,
AB=BE,CD=CE,AB+CD=BE+EC=30(厘米)
直角梯形 ABCD的面积:
(AB+CD)×BC÷2=30×30÷2=450(平方厘米)
故答案为:450。
梯形的面积=(上底+下底)×高÷2。
6.4.8
解:2.4×2=4.8(厘米)。
故答案为:4.8。
等底等高的平行四边形的面积是三角形面积的2倍,所以这个三角形的底=平行四边形的底×2。
7.50
解:10×5=50(平方厘米)。
故答案为:50。
阴影部分图形可以看作一个近似的底10厘米,高5厘米的平行四边形,面积=底×高。
8.437.5;875
解:50×17.5÷2=437.5(cm2),所以这个三角形的面积是437.5cm2;437.5×2=875(cm2),所以与它等底等高的平行四边形的面积是875cm2。
故答案为:437.5;875。
三角形的面积=底×高÷2;
等底等高三角形的面积是平行四边形面积的一半。
9.64;32
解:32÷(2-1)
=32÷1
=32(平方分米)
32×2=64(平方分米)
平行四边形面积是64平方分米,三角形面积是32平方分米。
故答案为:64;32。
根据等底等高的平行四边形面积是三角形的2倍,把三角形的面积看作1份,平行四边形的面积是2份,则相差(2-1)份,由此求出一份,进而求出平行四边形的面积。
10.24
解:12×2=24(厘米)。
故答案为:24。
等底等高的平行四边形的面积是三角形面积的2倍,三角形的高=平行四边形的高×2。
11.99
解:6×高-10×高÷2=9
6×高-5×高=9
高=9
(10+6+6)×9÷2=22×9÷2=99(平方厘米)
故答案为:99。
等量关系:平行四边形的面积-三角形的面积=9,据此求出他们的高;梯形的面积=(上底+下底)×高÷2,据此解答。
12.60
解:12×16÷2-12×6÷2
=96-36
=60(平方厘米)
故答案为:60。
观察图形,涂色部分面积等于大三角形面积减去小空白三角形的面积,根据三角形面积公式S=底×高÷2计算。
13.(1)C
(2)D
解:(1)连接BD,甲、乙两个三角形均和三角形BCD等底等高,所以甲、乙两个三角形均和三角形BCD的面积相同,则甲的面积等于乙的面积。
(2)根据两平行线之间的距离相等,可知,把一个平行四边形任意分割成两个梯形,这两个梯形的高一定相等
故答案为:C;D
(1)根据等高同底的性质和三角形的面积公式:S=底×高÷2即可判断
(2)根据两平行线之间的距离相等,据此即可解答。
14.B
解:将正方形右下角与长方形左下角相连接,
大三角形:8×(2+8)÷2=40(cm2)
小三角形:阴影部分:40+8=48(cm2)
做出辅助线后,可以看出阴影部分面积为两个三角形的面积之和。分别计算两个三角形的面积,两者相加即可。
15.D
解:假设高都是h厘米,
①6h÷2=3h;
②3h;
③(1.5+4.5)h÷2=3h;
所以它们的面积都相等。
故答案为:D。
三角形面积=底×高÷2,平行四边形面积=底×高,梯形面积=(上底+下底)×高÷2,假设它们的高都是h厘米;分别计算出面积,再比较面积的大小即可。
16.D
解:24÷(1+3)
=24÷4
=6(平方厘米)
故答案为:D。
根据图可知,阴影部分面积加上空白部分面积就是梯形的面积,由于两个三角形的高都是梯形的高,空白部分三角形的底是阴影部分三角形底的3倍,则阴影部分三角形的面积=梯形面积÷(1+3),代入数值计算即可解答。
17.D
解:
24÷12=2(平方厘米)
平行四边形ABCD的面积:2×9=18(平方厘米)
空白三角形①的面积:
2×6÷2
=12÷2
=6(平方厘米)
空白三角形②的面积:
2×3÷2
=6÷2
=3(平方厘米)
空白三角形③的面积:
2×2÷2
=4÷2
=2(平方厘米)
阴影部分的面积:
18-(6+3+2)
=18-11
=7(平方厘米)。
故答案为:D。
大平行四边形又被平均分成了12个小平行四边形,平均每个小平行四边形的面积是24÷12=2平方厘米,分别计算出①、②、③空白三角形的面积;阴影部分的面积=平行四边形ABCD的面积-三个空白三角形的面积和。
18.C
解:A和D的涂色部分的面积均占平行四边形面积的一半,B涂色部分的面积比平行四边形面积的一半多一些,C涂色部分的面积比平行四边形面积的一半少一些,所以C的涂色部分的面积最小。
故答案为:C。
根据等底等高判断出A和D的面积是平行四边形面积的一半;再去判断B和C涂色面积与平行四边形一半面积的关系。
19.B
解:平行四边形的面积是:S=ah1,
三角形的面积是:S=ah2÷2,
所以ah1=ah2÷2,
h1=h2÷2,
即:h2=2h1
所以h2:h1=2:1
故答案为:B。
根据平行四边形的面积公式S=ah及三角形的面积公式S=ah÷2,推导出在一个平行四边形和一个三角形的面积相等,底边长相等时,高的关系即可。
20.B
解:
A:阴影部分面积:,所以,A错误
B:阴影部分面积:,所以,B正确
C:阴影部分面积:,所以,C错误
故答案为:B
(1)利用阴影部分三角形的个数除以大三角中小三角的总个数,然后计算出阴影部分面积占大三角形比例即可
(2)根据阴影小平行四边形的个数除以大平行四边形中小平行四边形的总个数,然后计算出阴影部分面积占三角形比例即可
(3)利用阴影部分三角形的个数除以正方形中小三角的总个数,然后计算出阴影部分面积占正方形比例即可
21.C
解:A和D的涂色面积均占平行四边形面积的一半,B比平行四边形面积的一半多一些,C比平行四边形面积的一半少一些,所以C涂色面积最小。
故答案为:C。
根据涂颜色的形状,以及与平行四边形的面积大小关系进行比较得出结论。
22.C
连接OE,四边形ABCD 是一个边长是30厘米的正方形,E是CD的中点。
正方形ABCD ═ ×30×30 = 112.5(平方厘米)
BO=DO,CE=DE,OE是△BCD的中位线。
从而
(平方厘米)
同理可得 : (平方厘米)
(平方厘米)
故答案为:C。
因为E是正方形边的中点,所以可得△ADE的面积等于正方形面积的四分之一,△AFB∽△EDF,则DE:AB=EF:FA=1:2,可以得到△EDF的面积=×△ADE的面积=×正方形面积=×正方形面积。同理可证,△CEG的面积=×正方形面积。进而求出阴影部分的面积即可。
23.解:平行四边形的底画4格,高画3格,平行四边形面积=4×3=12(平方厘米)
三角形的底画8格,高画3格,平行四边形面积=8×3÷2=12(平方厘米)
梯形的上底画3格,下底画5格,高画3格,梯形面积=(3+5)×3÷2=12(平方厘米)
平行四边形面积=底×高,三角形面积=底×高÷2,梯形面积=(上底+下底)×高÷2,据此作图。
24.(1)解:
(2)解:(2+4)×2÷2
=6×2÷2
=12÷2
=6(平方厘米)
2×3=6(平方厘米)
(1)用数对表示位置时,前面一个数表示第几列,后面一个数表示第几行;列数一般从左往右数,行数一般从前往后数,顺次连接各点画出梯形;
(2)梯形的面积=(上底+下底)×高÷2,平行四边形的面积=底×高,依据梯形的面积计算出平行四边形底与高的格数,从而画出平行四边形。
25.25×2÷(3+7)=5( cm)
(7-3)×5÷2=10(cm2)
26.解:根据题意,可得
AB和DC的长度和:240×2÷12=40(m),
五条钢材的长度和:40+25+36.5×2=138(m),
138×320=44160(元)。
答:制作一个桥架需要44160元。
观察图形,根据梯形的面积公式:S=(上底+下底)×高÷2,可知,上底+下底=2S÷高,代入数据求出AB+DC的长度和;然后再求出五条钢材的长度和:40+25+36.5×2,最后再乘以每米钢材的成本价,即可求出总价钱。
27.解:2千米=2000米,
茶园的面积为2000×600÷2=600000(平方米)。
600000平方米=60公顷,
60×1600=96000(千克),
96000千克=96吨。
答:这块茶园的面积为60公顷,可产茶叶96吨。
根据1千米=1000米,1公顷=10000平方米,1吨=10000千克进行单位的换算;根据三角形面积=底×高÷2求出茶园的面积,再根据每公顷产茶叶1600千克求出茶园一共可产茶叶多少吨。
28.解:1公顷=10000平方米。
原遗址长:10000÷50=200(米),
原遗址面积:200×(200-50)=30000(平方米),
30000平方米=3公顷,
答:原遗址面积为3公顷。
首先将公顷换算成平方米,其中1公顷=10000平方米;增加后的遗址是一个正方形,用增加的面积除以增加的宽度得到原遗址的长度,用原遗址长减去增加的长度得到原遗址的宽度,据此求出原遗址的面积,再将结果的单位换算成公顷。
29.解: 平行四边形面积:0.9×0.4=0.36(平方厘米),
三角形面积:12×5÷2=30(平方厘米),
梯形面积:
(8+12)×15÷2
=20×15÷2
=150(平方厘米)
图形 平行四边形 三角形 梯形
底/cm 0.9 12 上底8下底12
高/cm 0.4 5 15
面积/cm2 0.36 30 150
平行四边形面积=底×高,三角形面积=底×高÷2,梯形面积=(上底+下底)×高÷2,根据公式计算并填表即可。
同课章节目录
