第八章 平行线的有关证明 检测题 (含答案)
文档属性
| 名称 | 第八章 平行线的有关证明 检测题 (含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 11.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-01-23 21:30:32 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
第八章检测题
时间:90分钟 满分: 150分
一、选择题(每题4分,共 40分)
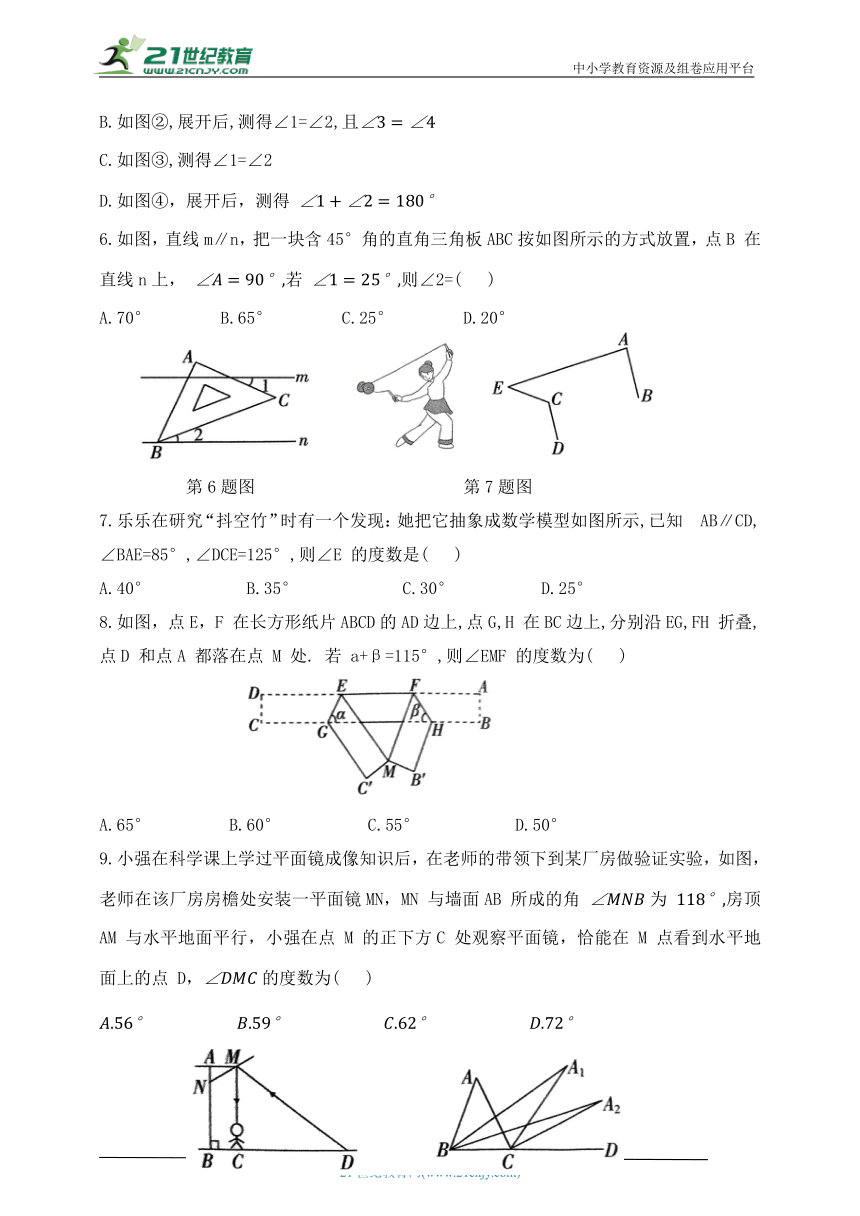
1.下面四个图形中,∠1=∠2一定成立的是( )
2.下列命题是真命题的是( )
A.如果两个角不相等,那么这两个角不是对顶角
B.如果两个数的和是正数,那么这两个数都是正数
C.如果 那么a=b
D.如果两个角是同位角,那么这两个角一定相等
3.如图,直线 , 被直线 , 所截,下列条件中,不能判定直线 ∥ 的是( )
A.∠1=∠3 B.∠5=∠4 C.∠5+∠3=180°
第3题图 第4题图
4.如图,直线a,b 被c,d 所截,且a∥b,则下列结论中正确的是( )
A.∠1=∠2 B.∠3=∠4
5.以下四种沿 AB 折叠的方法中,不一定能判定纸条两条边线a,b互相平行的是( )
A.如图①,展开后,测得
B.如图②,展开后,测得∠1=∠2,且
C.如图③,测得∠1=∠2
D.如图④,展开后,测得
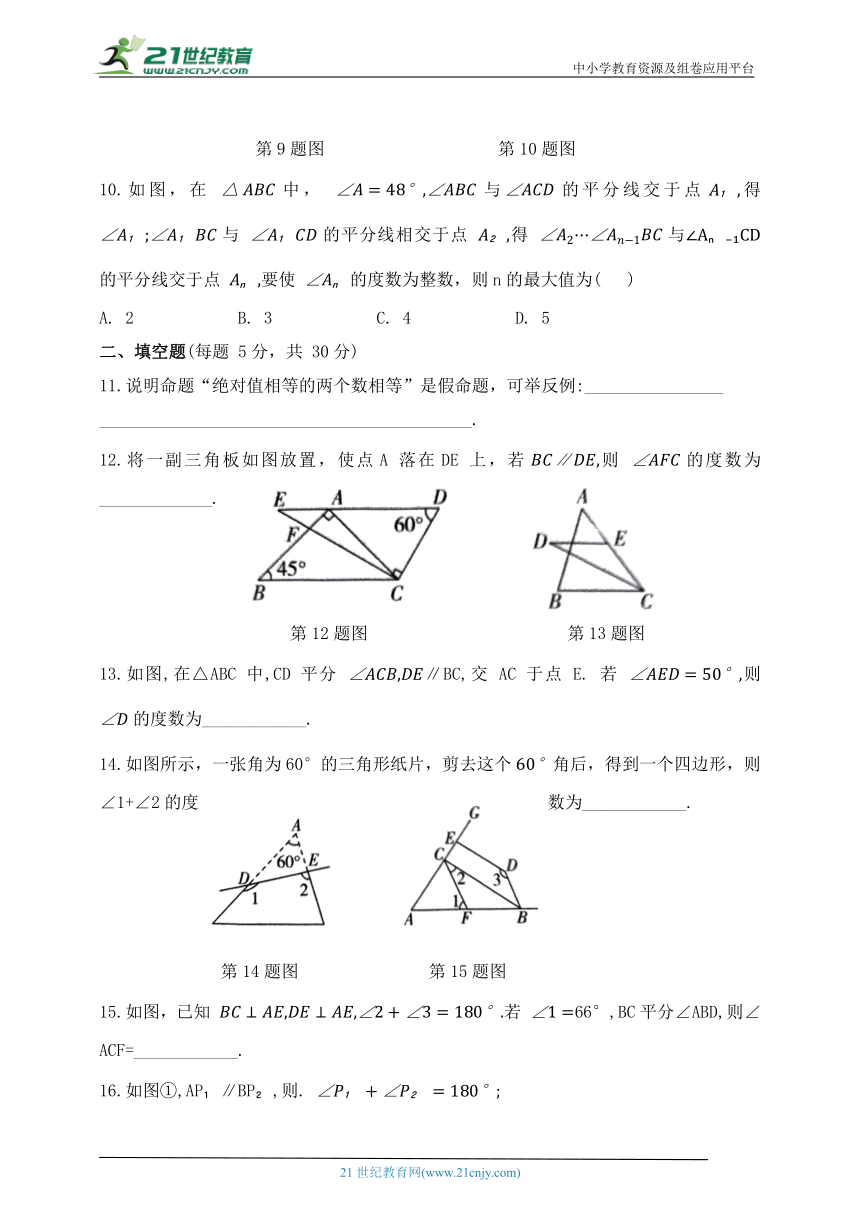
6.如图,直线m∥n,把一块含45°角的直角三角板ABC按如图所示的方式放置,点B 在直线n上, 若 则∠2=( )
A.70° B.65° C.25° D.20°
第6题图 第7题图
7.乐乐在研究“抖空竹”时有一个发现:她把它抽象成数学模型如图所示,已知 AB∥CD,∠BAE=85°,∠DCE=125°,则∠E 的度数是( )
A.40° B.35° C.30° D.25°
8.如图,点E,F 在长方形纸片ABCD的AD边上,点G,H 在BC边上,分别沿EG,FH 折叠,点D 和点A 都落在点 M 处. 若 a+β=115°,则∠EMF 的度数为( )
A.65° B.60° C.55° D.50°
9.小强在科学课上学过平面镜成像知识后,在老师的带领下到某厂房做验证实验,如图,老师在该厂房房檐处安装一平面镜MN,MN 与墙面AB 所成的角 为 房顶AM 与水平地面平行,小强在点 M 的正下方C 处观察平面镜,恰能在 M 点看到水平地面上的点 D,的度数为( )
第9题图 第10题图
10.如图,在 中, 与的平分线交于点得 与 的平分线相交于点 得 与的平分线交于点 要使 的度数为整数,则n的最大值为( )
A. 2 B. 3 C. 4 D. 5
二、填空题(每题 5分,共 30分)
11.说明命题“绝对值相等的两个数相等”是假命题,可举反例:________________
___________________________________________.
12.将一副三角板如图放置,使点A 落在DE 上,若∥则 的度数为_____________.
第12题图 第13题图
13.如图,在△ABC 中,CD 平分 ∥BC,交 AC 于点 E. 若 则 的度数为____________.
14.如图所示,一张角为60°的三角形纸片,剪去这个角后,得到一个四边形,则∠1+∠2的度数为____________.
第14题图 第15题图
15.如图,已知 若 66°,BC平分∠ABD,则∠ACF=____________.
16.如图①,AP ∥BP ,则.
如图②,AP ∥BP ,则
如图③,AP ∥BP ,则.
如图④,则第n个图中的(用含 n的代数式表示)
三、解答题(共 80分)
17. 10分如图, ∥的顶点F,G分别落在直线AB,CD 上,GE 交AB 于点H,GE 平分若 求 的度数.
18.12分 如图,直线CD,EF 交于点O, 且
(1)求证:AB∥CD.
(2)若OB 平分∠DOE,∠2:∠3=2:5,求∠AOF 的度数.
19.12分 如图,在 中,AD平分交BC于点D,点F 在BA 的延长线上,点 E 在线段CD 上,EF 与AC 相交于点G,AD∥EF.
(1)求证:
(2)若点 H 在 FE 的延长线上,且 则 与 相等吗 请说明理由.
20.15分 如图,CD∥EF,AE 是 的平分线,∠α和∠β的度数满足方程组 .
(1)求α和β的度数.
(2)求证:AB∥CD.
(3)求∠C 的度数.
21.15分 已知 ∥在AB,CD 内有一条折线EGF.
(1)如图①,过点 G 作GH∥AB,试说明: ∠EGF.
(2)如图②,已知∠BEG 的平分线与 的平分线相交于点Q,运用(1)中结论探究∠EGF 与 的数量关系,并说明理由.
【拓展应用】如图②,若 则∠Q 的度数为____________.(用含n,m的代数式表示)
22.16分 [新考向]综合与实践
数学课上,老师提出问题:如图,钓板上存在三条互相平行的直线AB,CD,EF,图①中弹性皮筋两端点用钉子固定在点M,N处,拉住皮筋中部的一点至点O 处固定,点O在直线CD上, 若 求∠2的度数.
【数学思考】(1)完成老师提出的问题.
【深入探究】(2)老师让同学们在图①的基础上,通过移动点O的位置或添加皮筋的方式增设条件来提出新的问题.
(Ⅰ)“善思小组”提出问题:如图②,在图①的基础上,将另一根弹性皮筋的一端固定在点O处,另一端用钉子固定在点 P 处.若∠PON=45°,求∠1-∠3的值.
(Ⅱ)“智慧小组”提出问题:如图③,在OM 与AB 的交点处用钉子固定点G,在ON 与EF 的交点处用钉子固定点H,将点O移动到点Q处(点 Q 在直线CD上).若 ∠GQH=70°,请直接写出∠MGQ+∠QHN 的值.
参考答案
1. B 2. A 3. B 4. B 5. C 6. D 7. A 8. D 9. A
10. C [解析]∵∠ABC 与∠ACD 的平分线交于点
同理可得 。要使 的度数为整数,则n
的最大值为4.
11.|-1|=|1|,而-1≠1(答案不唯一)
12. 75° 13.25° 14. 240° 15. 57° 16. 180°n
17.解:∵∠EFG=90°,∠E=35°,∴∠FGH=55°.
∵GE 平分∠FGD,AB∥CD,∴∠FHG=∠HGD=∠FGH=55°.
∵∠FHG 是△EFH 的外角,∴∠EFB=55°-35°=20°.
18.(1)证明:∵AO⊥BO,∴∠AOB=90°,∴∠AOC+∠2=90°.
∵∠1+∠2=90°,∴∠AOC=∠1,∴AB∥CD.
(2)解:∵OB 平分∠DOE,∴∠EOB=∠2.
∵∠2 :∠3=2:5,设∠2=∠EOB=2x,∠3=5x,则∠EOB+∠2+∠3=180°,即 2x+2x+5x= 180°,解得 x =20°,∴∠EOB=40°.
又∵∠AOB=90°,∴∠AOE=∠AOB-∠EOB=50°,∴∠AOF=180°-∠AOE=130°.
19.(1)证明:∵AD∥EF,∴∠BDA=∠BEF.
∵∠BEF+∠CEG=180°,∴∠BDA+∠CEG=180°.
(2)解:∠EDH=∠C.理由:∵AD 平分∠BAC,∴∠BAD=∠CAD.
∵AD∥EF,∴∠BAD=∠F,∠DAC=∠EGC,∴∠F=∠EGC.
∵∠H=∠F,∴∠H=∠EGC,∴HD∥AC,∴∠EDH=∠C.
20.(1)解:①+②,得5α=350°,∴α=70°.
把α=70°代入①, 得β=110°,∴α=70°,β=110°.
(2)证明:∵α+β=180°,∴AB∥EF.
∵CD∥EF,∴AB∥CD.
(3)解:∵AE 是∠CAB 的平分线,∴∠CAB=2α=140°.
∵AB∥CD,∴∠C+∠CAB=180°,∴∠C=40°.
21.解:(1)∵GH∥AB,∴∠BEG=∠EGH.
∵AB∥CD,∴GH∥CD,∴∠DFG=∠FGH.
∵∠EGH+∠FGH=∠EGF,∴∠BEG+∠DFG=∠EGF.
(2)∠EQF = 理由:
由(1)可得∠BEG+∠DFG=∠EGF,∠BEQ+∠DFQ=∠EQF.
∵EQ 平分∠BEG,FQ平分
即
【拓展应用】
22.解:∥.
∥
∥=15°.
(Ⅱ)130°.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
第八章检测题
时间:90分钟 满分: 150分
一、选择题(每题4分,共 40分)
1.下面四个图形中,∠1=∠2一定成立的是( )
2.下列命题是真命题的是( )
A.如果两个角不相等,那么这两个角不是对顶角
B.如果两个数的和是正数,那么这两个数都是正数
C.如果 那么a=b
D.如果两个角是同位角,那么这两个角一定相等
3.如图,直线 , 被直线 , 所截,下列条件中,不能判定直线 ∥ 的是( )
A.∠1=∠3 B.∠5=∠4 C.∠5+∠3=180°
第3题图 第4题图
4.如图,直线a,b 被c,d 所截,且a∥b,则下列结论中正确的是( )
A.∠1=∠2 B.∠3=∠4
5.以下四种沿 AB 折叠的方法中,不一定能判定纸条两条边线a,b互相平行的是( )
A.如图①,展开后,测得
B.如图②,展开后,测得∠1=∠2,且
C.如图③,测得∠1=∠2
D.如图④,展开后,测得
6.如图,直线m∥n,把一块含45°角的直角三角板ABC按如图所示的方式放置,点B 在直线n上, 若 则∠2=( )
A.70° B.65° C.25° D.20°
第6题图 第7题图
7.乐乐在研究“抖空竹”时有一个发现:她把它抽象成数学模型如图所示,已知 AB∥CD,∠BAE=85°,∠DCE=125°,则∠E 的度数是( )
A.40° B.35° C.30° D.25°
8.如图,点E,F 在长方形纸片ABCD的AD边上,点G,H 在BC边上,分别沿EG,FH 折叠,点D 和点A 都落在点 M 处. 若 a+β=115°,则∠EMF 的度数为( )
A.65° B.60° C.55° D.50°
9.小强在科学课上学过平面镜成像知识后,在老师的带领下到某厂房做验证实验,如图,老师在该厂房房檐处安装一平面镜MN,MN 与墙面AB 所成的角 为 房顶AM 与水平地面平行,小强在点 M 的正下方C 处观察平面镜,恰能在 M 点看到水平地面上的点 D,的度数为( )
第9题图 第10题图
10.如图,在 中, 与的平分线交于点得 与 的平分线相交于点 得 与的平分线交于点 要使 的度数为整数,则n的最大值为( )
A. 2 B. 3 C. 4 D. 5
二、填空题(每题 5分,共 30分)
11.说明命题“绝对值相等的两个数相等”是假命题,可举反例:________________
___________________________________________.
12.将一副三角板如图放置,使点A 落在DE 上,若∥则 的度数为_____________.
第12题图 第13题图
13.如图,在△ABC 中,CD 平分 ∥BC,交 AC 于点 E. 若 则 的度数为____________.
14.如图所示,一张角为60°的三角形纸片,剪去这个角后,得到一个四边形,则∠1+∠2的度数为____________.
第14题图 第15题图
15.如图,已知 若 66°,BC平分∠ABD,则∠ACF=____________.
16.如图①,AP ∥BP ,则.
如图②,AP ∥BP ,则
如图③,AP ∥BP ,则.
如图④,则第n个图中的(用含 n的代数式表示)
三、解答题(共 80分)
17. 10分如图, ∥的顶点F,G分别落在直线AB,CD 上,GE 交AB 于点H,GE 平分若 求 的度数.
18.12分 如图,直线CD,EF 交于点O, 且
(1)求证:AB∥CD.
(2)若OB 平分∠DOE,∠2:∠3=2:5,求∠AOF 的度数.
19.12分 如图,在 中,AD平分交BC于点D,点F 在BA 的延长线上,点 E 在线段CD 上,EF 与AC 相交于点G,AD∥EF.
(1)求证:
(2)若点 H 在 FE 的延长线上,且 则 与 相等吗 请说明理由.
20.15分 如图,CD∥EF,AE 是 的平分线,∠α和∠β的度数满足方程组 .
(1)求α和β的度数.
(2)求证:AB∥CD.
(3)求∠C 的度数.
21.15分 已知 ∥在AB,CD 内有一条折线EGF.
(1)如图①,过点 G 作GH∥AB,试说明: ∠EGF.
(2)如图②,已知∠BEG 的平分线与 的平分线相交于点Q,运用(1)中结论探究∠EGF 与 的数量关系,并说明理由.
【拓展应用】如图②,若 则∠Q 的度数为____________.(用含n,m的代数式表示)
22.16分 [新考向]综合与实践
数学课上,老师提出问题:如图,钓板上存在三条互相平行的直线AB,CD,EF,图①中弹性皮筋两端点用钉子固定在点M,N处,拉住皮筋中部的一点至点O 处固定,点O在直线CD上, 若 求∠2的度数.
【数学思考】(1)完成老师提出的问题.
【深入探究】(2)老师让同学们在图①的基础上,通过移动点O的位置或添加皮筋的方式增设条件来提出新的问题.
(Ⅰ)“善思小组”提出问题:如图②,在图①的基础上,将另一根弹性皮筋的一端固定在点O处,另一端用钉子固定在点 P 处.若∠PON=45°,求∠1-∠3的值.
(Ⅱ)“智慧小组”提出问题:如图③,在OM 与AB 的交点处用钉子固定点G,在ON 与EF 的交点处用钉子固定点H,将点O移动到点Q处(点 Q 在直线CD上).若 ∠GQH=70°,请直接写出∠MGQ+∠QHN 的值.
参考答案
1. B 2. A 3. B 4. B 5. C 6. D 7. A 8. D 9. A
10. C [解析]∵∠ABC 与∠ACD 的平分线交于点
同理可得 。要使 的度数为整数,则n
的最大值为4.
11.|-1|=|1|,而-1≠1(答案不唯一)
12. 75° 13.25° 14. 240° 15. 57° 16. 180°n
17.解:∵∠EFG=90°,∠E=35°,∴∠FGH=55°.
∵GE 平分∠FGD,AB∥CD,∴∠FHG=∠HGD=∠FGH=55°.
∵∠FHG 是△EFH 的外角,∴∠EFB=55°-35°=20°.
18.(1)证明:∵AO⊥BO,∴∠AOB=90°,∴∠AOC+∠2=90°.
∵∠1+∠2=90°,∴∠AOC=∠1,∴AB∥CD.
(2)解:∵OB 平分∠DOE,∴∠EOB=∠2.
∵∠2 :∠3=2:5,设∠2=∠EOB=2x,∠3=5x,则∠EOB+∠2+∠3=180°,即 2x+2x+5x= 180°,解得 x =20°,∴∠EOB=40°.
又∵∠AOB=90°,∴∠AOE=∠AOB-∠EOB=50°,∴∠AOF=180°-∠AOE=130°.
19.(1)证明:∵AD∥EF,∴∠BDA=∠BEF.
∵∠BEF+∠CEG=180°,∴∠BDA+∠CEG=180°.
(2)解:∠EDH=∠C.理由:∵AD 平分∠BAC,∴∠BAD=∠CAD.
∵AD∥EF,∴∠BAD=∠F,∠DAC=∠EGC,∴∠F=∠EGC.
∵∠H=∠F,∴∠H=∠EGC,∴HD∥AC,∴∠EDH=∠C.
20.(1)解:①+②,得5α=350°,∴α=70°.
把α=70°代入①, 得β=110°,∴α=70°,β=110°.
(2)证明:∵α+β=180°,∴AB∥EF.
∵CD∥EF,∴AB∥CD.
(3)解:∵AE 是∠CAB 的平分线,∴∠CAB=2α=140°.
∵AB∥CD,∴∠C+∠CAB=180°,∴∠C=40°.
21.解:(1)∵GH∥AB,∴∠BEG=∠EGH.
∵AB∥CD,∴GH∥CD,∴∠DFG=∠FGH.
∵∠EGH+∠FGH=∠EGF,∴∠BEG+∠DFG=∠EGF.
(2)∠EQF = 理由:
由(1)可得∠BEG+∠DFG=∠EGF,∠BEQ+∠DFQ=∠EQF.
∵EQ 平分∠BEG,FQ平分
即
【拓展应用】
22.解:∥.
∥
∥=15°.
(Ⅱ)130°.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
- 第七章 二元一次方程组
- 1 二元一次方程组
- 2 解二元一次方程组
- 3 二元一次方程组的应用
- 4 二元一次方程与一次函数
- *5 三元一次方程组
- 第八章 平行线的有关证明
- 1 定义与命题
- 2 证明的必要性
- 3 基本事实与定理
- 4 平行线的判定定理
- 5 平行线的性质定理
- 6 三角形内角和定理
- 第九章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
- 第十章 三角形的有关证明
- 1 全等三角形
- 2 等腰三角形
- 3 直角三角形
- 4 线段的垂直平分线
- 5 角平分线
- 第十一章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
