第八章 平行线的有关证明 5 平行线的性质定理 同步练习(含答案)
文档属性
| 名称 | 第八章 平行线的有关证明 5 平行线的性质定理 同步练习(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 5.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-01-23 21:37:39 | ||
图片预览

文档简介
中小学教育资源及组卷应用平台
第八章 平行线的有关证明
5 平行线的性质定理
基础闯关
知识点一:平行线的性质定理
1.已知,直线 ∥把一块含有 角的直角三角板如图放置,三角板的斜边所在直线交 b于点A,则
C.70°
第1题图 第2题图
2.如图,AB∥DC,BC∥DE,∠B=145°,则∠D 的度数为( )
A.25° B.35° C.45° D.55°
3.将直尺、三角板、量角器如图放置,则∠1的度数是( )
A.38° B.40° C.48° D.52°
4.将一副三角板按如图所示摆放在一组平行线内,若∠1=25°,∠2=30°,则∠3的度数为( )
A.55° B.65° C.70° D.75°
第4题图 第5题图
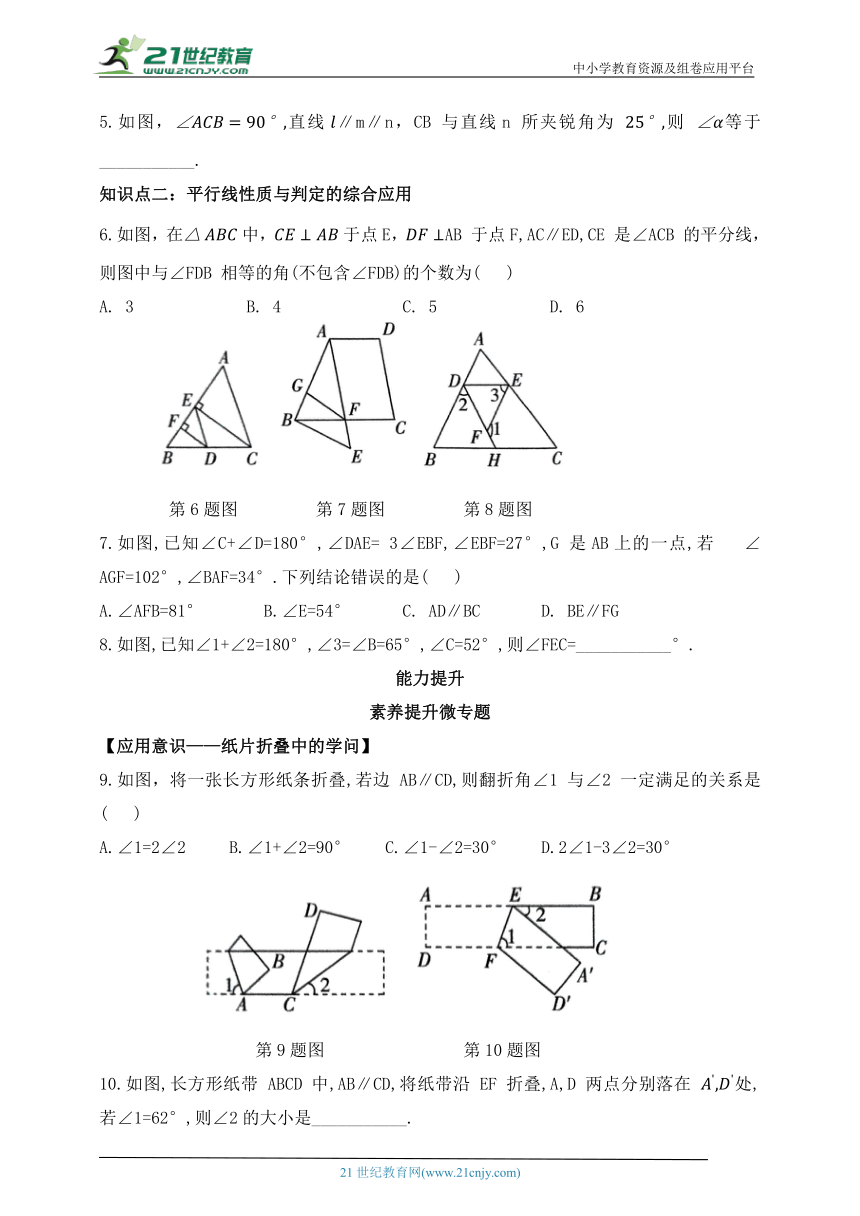
5.如图,直线∥m∥n,CB 与直线n 所夹锐角为 则 等于___________.
知识点二:平行线性质与判定的综合应用
6.如图,在中,于点E,AB 于点F,AC∥ED,CE 是∠ACB 的平分线,则图中与∠FDB 相等的角(不包含∠FDB)的个数为( )
A. 3 B. 4 C. 5 D. 6
第6题图 第7题图 第8题图
7.如图,已知∠C+∠D=180°,∠DAE= 3∠EBF,∠EBF=27°,G 是AB上的一点,若 ∠AGF=102°,∠BAF=34°.下列结论错误的是( )
A.∠AFB=81° B.∠E=54° C. AD∥BC D. BE∥FG
8.如图,已知∠1+∠2=180°,∠3=∠B=65°,∠C=52°,则∠FEC=___________°.
能力提升
素养提升微专题
【应用意识——纸片折叠中的学问】
9.如图,将一张长方形纸条折叠,若边 AB∥CD,则翻折角∠1 与∠2 一定满足的关系是( )
A.∠1=2∠2 B.∠1+∠2=90° C.∠1-∠2=30° D.2∠1-3∠2=30°
第9题图 第10题图
10.如图,长方形纸带 ABCD 中,AB∥CD,将纸带沿 EF 折叠,A,D 两点分别落在 处,若∠1=62°,则∠2的大小是___________.
【探究角的数量关系】
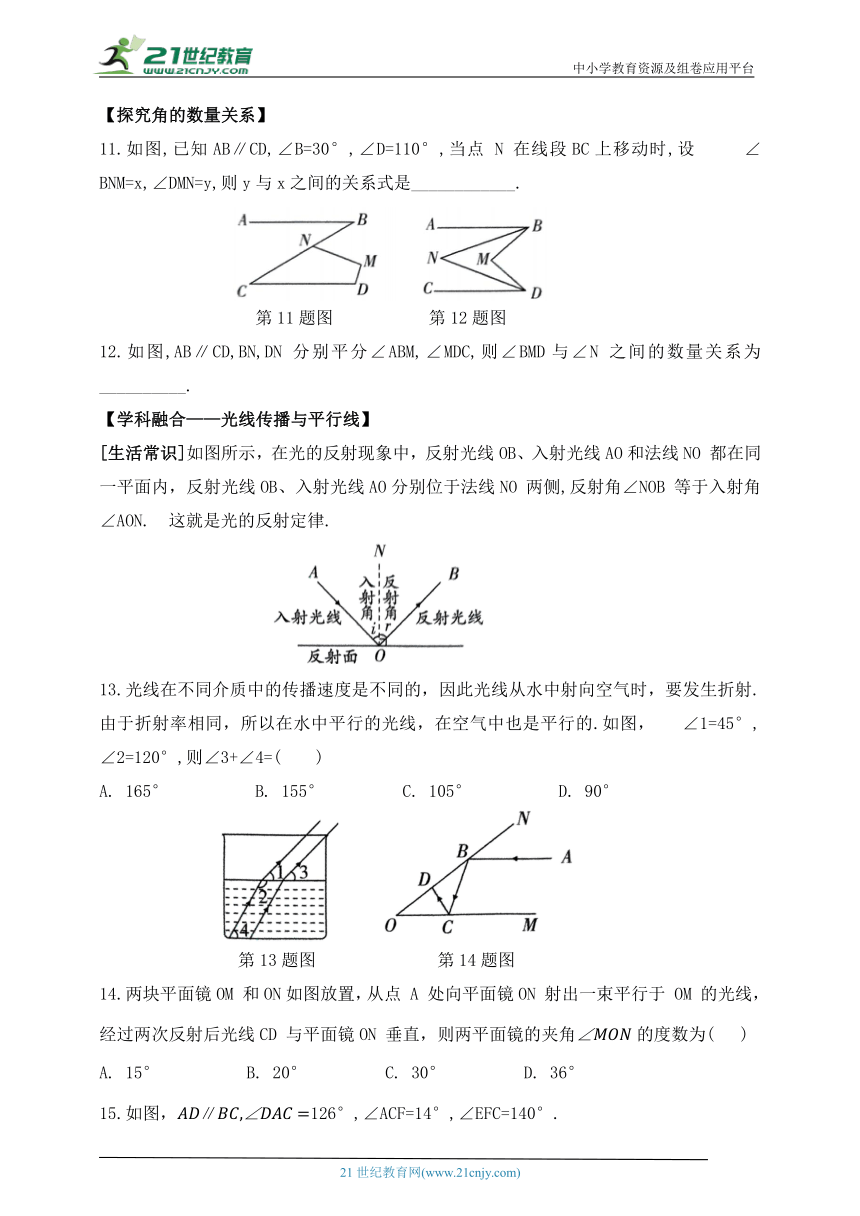
11.如图,已知AB∥CD,∠B=30°,∠D=110°,当点 N 在线段BC上移动时,设 ∠BNM=x,∠DMN=y,则y与x之间的关系式是____________.
第11题图 第12题图
12.如图,AB∥CD,BN,DN 分别平分∠ABM,∠MDC,则∠BMD与∠N 之间的数量关系为__________.
【学科融合——光线传播与平行线】
[生活常识]如图所示,在光的反射现象中,反射光线OB、入射光线AO和法线NO 都在同一平面内,反射光线OB、入射光线AO分别位于法线NO 两侧,反射角∠NOB 等于入射角∠AON. 这就是光的反射定律.
13.光线在不同介质中的传播速度是不同的,因此光线从水中射向空气时,要发生折射.由于折射率相同,所以在水中平行的光线,在空气中也是平行的.如图, ∠1=45°,∠2=120°,则∠3+∠4=( )
A. 165° B. 155° C. 105° D. 90°
第13题图 第14题图
14.两块平面镜OM 和ON如图放置,从点 A 处向平面镜ON 射出一束平行于 OM 的光线,经过两次反射后光线CD 与平面镜ON 垂直,则两平面镜的夹角的度数为( )
A. 15° B. 20° C. 30° D. 36°
15.如图,∥126°,∠ACF=14°,∠EFC=140°.
(1)求证:EF∥AD.
(2)连接CE,若CE 平分∠BCF,求∠FEC的度数.
培优创新
素养提升微专题
【几何直观——三角尺拼摆中的结论探究】
16.将一副三角板的直角顶点重合按如图放置,小明得到下列结论:
①若 则AC∥DE;②∠BAE+③若 ∥则
④若 则 其中正确的结论有( )
A.1个 B.2个 C.3个 D.4个
参考答案
1. B 2. B 3. A 4. C 5. 65° 6. B 7. D 8. 63 9. B
10.56°
11. y=x+40° [解析] ∵AB∥CD,∴∠B=∠C=30°.
∵∠BNM=x,∴∠MNC=180°-∠BNM=180°-x.
∵∠D=110°,∠DMN=y,∴∠C+∠D+∠DMN+∠MNC=30°+110°+y+180°-x=360°,
∴y=x+40°.
12.∠BMD=2∠N [解析]如图,过点 M 作 ME∥AB,则∠ABM=∠BME.
∵AB∥CD,ME∥AB,∴ME∥CD,∴∠CDM=∠DME,∴∠ABM+∠CDM=∠BME+∠DME =∠BMD.
同理,∠N =∠ABN +∠CDN.
∵BN,DN 分别平分∠ABM,∠MDC,∴∠ABM=2∠ABN,∠CDM=2∠CDN,
∴∠ABM+∠CDM=2∠ABN+2∠CDN=2∠N,∴∠BMD=2∠N.
13. C 14. C
15.(1)证明:∵AD∥BC,∴∠ACB+∠DAC=180°.
∵∠DAC=126°,∴∠ACB=54°.
又∵∠ACF=14°,
∥∥
(2)解:由(1)知. 又∵CE 平分
∥
16. C
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
第八章 平行线的有关证明
5 平行线的性质定理
基础闯关
知识点一:平行线的性质定理
1.已知,直线 ∥把一块含有 角的直角三角板如图放置,三角板的斜边所在直线交 b于点A,则
C.70°
第1题图 第2题图
2.如图,AB∥DC,BC∥DE,∠B=145°,则∠D 的度数为( )
A.25° B.35° C.45° D.55°
3.将直尺、三角板、量角器如图放置,则∠1的度数是( )
A.38° B.40° C.48° D.52°
4.将一副三角板按如图所示摆放在一组平行线内,若∠1=25°,∠2=30°,则∠3的度数为( )
A.55° B.65° C.70° D.75°
第4题图 第5题图
5.如图,直线∥m∥n,CB 与直线n 所夹锐角为 则 等于___________.
知识点二:平行线性质与判定的综合应用
6.如图,在中,于点E,AB 于点F,AC∥ED,CE 是∠ACB 的平分线,则图中与∠FDB 相等的角(不包含∠FDB)的个数为( )
A. 3 B. 4 C. 5 D. 6
第6题图 第7题图 第8题图
7.如图,已知∠C+∠D=180°,∠DAE= 3∠EBF,∠EBF=27°,G 是AB上的一点,若 ∠AGF=102°,∠BAF=34°.下列结论错误的是( )
A.∠AFB=81° B.∠E=54° C. AD∥BC D. BE∥FG
8.如图,已知∠1+∠2=180°,∠3=∠B=65°,∠C=52°,则∠FEC=___________°.
能力提升
素养提升微专题
【应用意识——纸片折叠中的学问】
9.如图,将一张长方形纸条折叠,若边 AB∥CD,则翻折角∠1 与∠2 一定满足的关系是( )
A.∠1=2∠2 B.∠1+∠2=90° C.∠1-∠2=30° D.2∠1-3∠2=30°
第9题图 第10题图
10.如图,长方形纸带 ABCD 中,AB∥CD,将纸带沿 EF 折叠,A,D 两点分别落在 处,若∠1=62°,则∠2的大小是___________.
【探究角的数量关系】
11.如图,已知AB∥CD,∠B=30°,∠D=110°,当点 N 在线段BC上移动时,设 ∠BNM=x,∠DMN=y,则y与x之间的关系式是____________.
第11题图 第12题图
12.如图,AB∥CD,BN,DN 分别平分∠ABM,∠MDC,则∠BMD与∠N 之间的数量关系为__________.
【学科融合——光线传播与平行线】
[生活常识]如图所示,在光的反射现象中,反射光线OB、入射光线AO和法线NO 都在同一平面内,反射光线OB、入射光线AO分别位于法线NO 两侧,反射角∠NOB 等于入射角∠AON. 这就是光的反射定律.
13.光线在不同介质中的传播速度是不同的,因此光线从水中射向空气时,要发生折射.由于折射率相同,所以在水中平行的光线,在空气中也是平行的.如图, ∠1=45°,∠2=120°,则∠3+∠4=( )
A. 165° B. 155° C. 105° D. 90°
第13题图 第14题图
14.两块平面镜OM 和ON如图放置,从点 A 处向平面镜ON 射出一束平行于 OM 的光线,经过两次反射后光线CD 与平面镜ON 垂直,则两平面镜的夹角的度数为( )
A. 15° B. 20° C. 30° D. 36°
15.如图,∥126°,∠ACF=14°,∠EFC=140°.
(1)求证:EF∥AD.
(2)连接CE,若CE 平分∠BCF,求∠FEC的度数.
培优创新
素养提升微专题
【几何直观——三角尺拼摆中的结论探究】
16.将一副三角板的直角顶点重合按如图放置,小明得到下列结论:
①若 则AC∥DE;②∠BAE+③若 ∥则
④若 则 其中正确的结论有( )
A.1个 B.2个 C.3个 D.4个
参考答案
1. B 2. B 3. A 4. C 5. 65° 6. B 7. D 8. 63 9. B
10.56°
11. y=x+40° [解析] ∵AB∥CD,∴∠B=∠C=30°.
∵∠BNM=x,∴∠MNC=180°-∠BNM=180°-x.
∵∠D=110°,∠DMN=y,∴∠C+∠D+∠DMN+∠MNC=30°+110°+y+180°-x=360°,
∴y=x+40°.
12.∠BMD=2∠N [解析]如图,过点 M 作 ME∥AB,则∠ABM=∠BME.
∵AB∥CD,ME∥AB,∴ME∥CD,∴∠CDM=∠DME,∴∠ABM+∠CDM=∠BME+∠DME =∠BMD.
同理,∠N =∠ABN +∠CDN.
∵BN,DN 分别平分∠ABM,∠MDC,∴∠ABM=2∠ABN,∠CDM=2∠CDN,
∴∠ABM+∠CDM=2∠ABN+2∠CDN=2∠N,∴∠BMD=2∠N.
13. C 14. C
15.(1)证明:∵AD∥BC,∴∠ACB+∠DAC=180°.
∵∠DAC=126°,∴∠ACB=54°.
又∵∠ACF=14°,
∥∥
(2)解:由(1)知. 又∵CE 平分
∥
16. C
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
- 第七章 二元一次方程组
- 1 二元一次方程组
- 2 解二元一次方程组
- 3 二元一次方程组的应用
- 4 二元一次方程与一次函数
- *5 三元一次方程组
- 第八章 平行线的有关证明
- 1 定义与命题
- 2 证明的必要性
- 3 基本事实与定理
- 4 平行线的判定定理
- 5 平行线的性质定理
- 6 三角形内角和定理
- 第九章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
- 第十章 三角形的有关证明
- 1 全等三角形
- 2 等腰三角形
- 3 直角三角形
- 4 线段的垂直平分线
- 5 角平分线
- 第十一章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
