第八章 平行线的有关证明 6 三角形的内角和定理 第1课时 三角形内角和定理 同步练习(含答案)
文档属性
| 名称 | 第八章 平行线的有关证明 6 三角形的内角和定理 第1课时 三角形内角和定理 同步练习(含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 4.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-01-23 21:37:19 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
第八章 平行线的有关证明
6 三角形的内角和定理
第1课时 三角形内角和定理
基础闯关
知识点一:三角形内角和定理
命题角度1:应用三角形内角和定理求角度
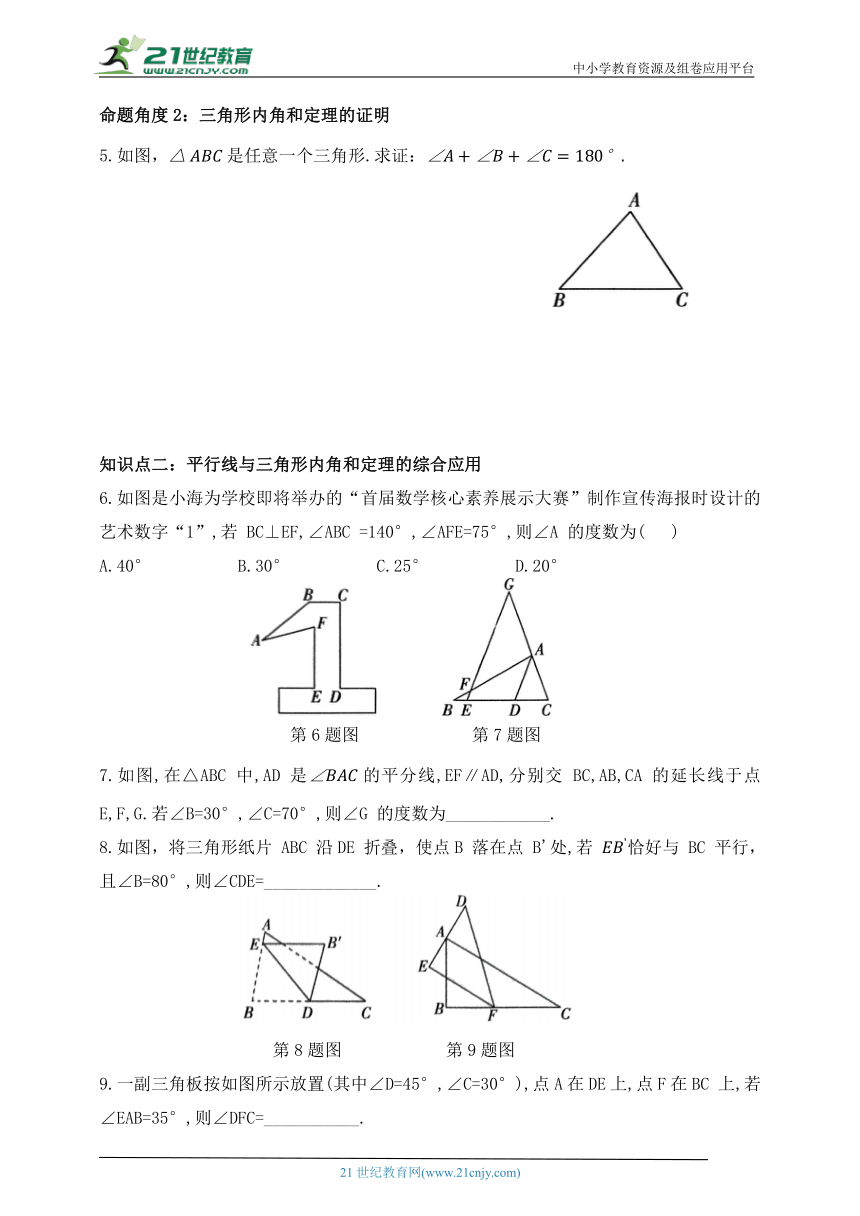
1.如图,考古学家发现在地下 A 处有一座古墓,古墓上方是煤气管道,为了不影响管道,准备在 B 和C 处开工挖出“V”字形通道.若 ,则∠A 的度数是( )
B.80° C.85°
第1题图 第2题图
2.如图,在△ABC 中,AD 是的平分线,E为AD 上一点,且 BC 于点 F.若 则∠B 的度数为( )
A.60° B.65° C.75° D.85°
3.如图,线段AF⊥AE,垂足为点A,线段GD分别交AF,AE 于点C,B,连接GF,ED,则. 的度数为____________.
第3题图 第4题图
4.如图,在 中,∠A=40°,∠B=70°,CE平分于点D, 于点F,则
命题角度2:三角形内角和定理的证明
5.如图,是任意一个三角形.求证:
知识点二:平行线与三角形内角和定理的综合应用
6.如图是小海为学校即将举办的“首届数学核心素养展示大赛”制作宣传海报时设计的艺术数字“1”,若 BC⊥EF,∠ABC =140°,∠AFE=75°,则∠A 的度数为( )
A.40° B.30° C.25° D.20°
第6题图 第7题图
7.如图,在△ABC 中,AD 是的平分线,EF∥AD,分别交 BC,AB,CA 的延长线于点 E,F,G.若∠B=30°,∠C=70°,则∠G 的度数为____________.
8.如图,将三角形纸片 ABC 沿DE 折叠,使点B 落在点 B'处,若 恰好与 BC 平行,且∠B=80°,则∠CDE=_____________.
第8题图 第9题图
9.一副三角板按如图所示放置(其中∠D=45°,∠C=30°),点A在DE上,点F在BC 上,若∠EAB=35°,则∠DFC=___________.
能力提升
10.如图,点 A,B 分别在锐角∠MCN 的边CM,CN 上,射线CP 在∠MCN 的内部,点D,E 在射线CP 上.若AD∥BE,则∠CAD+∠ACB+∠CBE 等于( )
A.170° B.180° C.190° D.200°
11.[新考向·学科融合]如图所示是地球截面图,其中AB,EF 分别表示南回归线和北回归线,CD 表示赤道,点P 表示某市的位置.现已知地球南回归线的纬度是南纬 23°26'(∠BOD=23°26'),某个城市的纬度是北纬37°32'(∠POD=37°32'),而冬至正午时,太阳光(太阳光线都是互相平行的)直射南回归线(光线 MB 的延长线经过地心O),则这个城市冬至正午时,太阳光线NP 与地面水平线PQ 的夹角α的度数是_____________.
12.如图,已知BD 平分∠ABC,点F在AB 上,点G在AC 上,连接 FG,FC, FC 与BD 相交于点 H,∠1=∠2.
(1)求证:∠GFH 与∠BHC 互补.
(2)若∠A =75°,FG⊥AC,求∠ACB 的度数.
培优创新
13.[推理能力]如图①,AD 平分∠BAC,AE⊥BC,∠B=38°,∠C=64°.
(1)求∠DAE 的度数.
(2)如图②,若把变成“点 F 在DA 的延长线上,FE⊥BC”,∠B=α, ∠C=β(α<β),请用含α,β的代数式表示∠DFE.
参考答案
1. A 2. B 3. 270° 4. 75°
5.证明:如图,过点 A 作EF∥BC.
∵EF∥BC,∴∠1=∠B,∠2 = ∠C.
∵ ∠1 + ∠2 + ∠BAC = 180°,∴∠BAC+∠B+∠C=180°.
6. C [解析]如图,延长EF 交BC 于点H,过点 B 作BT⊥BC交AF于点 T.
∵BT⊥BC,∴∠TBC=90°.
∵∠ABC =140°,∴∠ABT=∠ABC-∠TBC=140°-90°=50°.
∵∠AFE=75°,∴∠AFH=180°-∠AFE=180°-75°=105°.
∵BC⊥EF,BT⊥BC,∴BT∥EF,∴∠ATB=∠AFH=105°.
∵∠A+∠ABT+∠ATB=180°,∴∠A
7.40° 8.130° 9.100° 10. B 11.29°2'
12.(1)证明:∵BD 平分∠ABC,∴∠2=∠ABD.
∵∠1=∠2,∴∠1=∠ABD,∴FG∥BD,∴∠GFH+∠FHD=180°.
∵∠BHC=∠FHD,∴∠GFH+∠BHC=180°, ∴∠GFH 与∠BHC 互补.
(2)解:∵∠A=75°,FG⊥AC,∴∠1=90°-75°=15°,∴∠2=∠1=15°.
∵BD平分∠ABC,∴∠ABC=30°,∴∠ACB=180°-∠A-∠ABC=180°-75°-30°=75°.
13.解:(1)∵∠B=38°,∠C=64°,∴∠BAC=78°.
∵AD 平分∠BAC,∴∠BAD=∠CAD=39°,∴∠ADE=180°-∠ADB=∠B+∠BAD=77°.
∵AE⊥BC,∴∠AEB=90°,∴∠DAE=90°-∠ADE=13°.
(2)∵∠B=α,∠C =β,∴∠BAC= 180°-α-β.
∵AD 平分∠BAC,
-α).
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
第八章 平行线的有关证明
6 三角形的内角和定理
第1课时 三角形内角和定理
基础闯关
知识点一:三角形内角和定理
命题角度1:应用三角形内角和定理求角度
1.如图,考古学家发现在地下 A 处有一座古墓,古墓上方是煤气管道,为了不影响管道,准备在 B 和C 处开工挖出“V”字形通道.若 ,则∠A 的度数是( )
B.80° C.85°
第1题图 第2题图
2.如图,在△ABC 中,AD 是的平分线,E为AD 上一点,且 BC 于点 F.若 则∠B 的度数为( )
A.60° B.65° C.75° D.85°
3.如图,线段AF⊥AE,垂足为点A,线段GD分别交AF,AE 于点C,B,连接GF,ED,则. 的度数为____________.
第3题图 第4题图
4.如图,在 中,∠A=40°,∠B=70°,CE平分于点D, 于点F,则
命题角度2:三角形内角和定理的证明
5.如图,是任意一个三角形.求证:
知识点二:平行线与三角形内角和定理的综合应用
6.如图是小海为学校即将举办的“首届数学核心素养展示大赛”制作宣传海报时设计的艺术数字“1”,若 BC⊥EF,∠ABC =140°,∠AFE=75°,则∠A 的度数为( )
A.40° B.30° C.25° D.20°
第6题图 第7题图
7.如图,在△ABC 中,AD 是的平分线,EF∥AD,分别交 BC,AB,CA 的延长线于点 E,F,G.若∠B=30°,∠C=70°,则∠G 的度数为____________.
8.如图,将三角形纸片 ABC 沿DE 折叠,使点B 落在点 B'处,若 恰好与 BC 平行,且∠B=80°,则∠CDE=_____________.
第8题图 第9题图
9.一副三角板按如图所示放置(其中∠D=45°,∠C=30°),点A在DE上,点F在BC 上,若∠EAB=35°,则∠DFC=___________.
能力提升
10.如图,点 A,B 分别在锐角∠MCN 的边CM,CN 上,射线CP 在∠MCN 的内部,点D,E 在射线CP 上.若AD∥BE,则∠CAD+∠ACB+∠CBE 等于( )
A.170° B.180° C.190° D.200°
11.[新考向·学科融合]如图所示是地球截面图,其中AB,EF 分别表示南回归线和北回归线,CD 表示赤道,点P 表示某市的位置.现已知地球南回归线的纬度是南纬 23°26'(∠BOD=23°26'),某个城市的纬度是北纬37°32'(∠POD=37°32'),而冬至正午时,太阳光(太阳光线都是互相平行的)直射南回归线(光线 MB 的延长线经过地心O),则这个城市冬至正午时,太阳光线NP 与地面水平线PQ 的夹角α的度数是_____________.
12.如图,已知BD 平分∠ABC,点F在AB 上,点G在AC 上,连接 FG,FC, FC 与BD 相交于点 H,∠1=∠2.
(1)求证:∠GFH 与∠BHC 互补.
(2)若∠A =75°,FG⊥AC,求∠ACB 的度数.
培优创新
13.[推理能力]如图①,AD 平分∠BAC,AE⊥BC,∠B=38°,∠C=64°.
(1)求∠DAE 的度数.
(2)如图②,若把变成“点 F 在DA 的延长线上,FE⊥BC”,∠B=α, ∠C=β(α<β),请用含α,β的代数式表示∠DFE.
参考答案
1. A 2. B 3. 270° 4. 75°
5.证明:如图,过点 A 作EF∥BC.
∵EF∥BC,∴∠1=∠B,∠2 = ∠C.
∵ ∠1 + ∠2 + ∠BAC = 180°,∴∠BAC+∠B+∠C=180°.
6. C [解析]如图,延长EF 交BC 于点H,过点 B 作BT⊥BC交AF于点 T.
∵BT⊥BC,∴∠TBC=90°.
∵∠ABC =140°,∴∠ABT=∠ABC-∠TBC=140°-90°=50°.
∵∠AFE=75°,∴∠AFH=180°-∠AFE=180°-75°=105°.
∵BC⊥EF,BT⊥BC,∴BT∥EF,∴∠ATB=∠AFH=105°.
∵∠A+∠ABT+∠ATB=180°,∴∠A
7.40° 8.130° 9.100° 10. B 11.29°2'
12.(1)证明:∵BD 平分∠ABC,∴∠2=∠ABD.
∵∠1=∠2,∴∠1=∠ABD,∴FG∥BD,∴∠GFH+∠FHD=180°.
∵∠BHC=∠FHD,∴∠GFH+∠BHC=180°, ∴∠GFH 与∠BHC 互补.
(2)解:∵∠A=75°,FG⊥AC,∴∠1=90°-75°=15°,∴∠2=∠1=15°.
∵BD平分∠ABC,∴∠ABC=30°,∴∠ACB=180°-∠A-∠ABC=180°-75°-30°=75°.
13.解:(1)∵∠B=38°,∠C=64°,∴∠BAC=78°.
∵AD 平分∠BAC,∴∠BAD=∠CAD=39°,∴∠ADE=180°-∠ADB=∠B+∠BAD=77°.
∵AE⊥BC,∴∠AEB=90°,∴∠DAE=90°-∠ADE=13°.
(2)∵∠B=α,∠C =β,∴∠BAC= 180°-α-β.
∵AD 平分∠BAC,
-α).
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
- 第七章 二元一次方程组
- 1 二元一次方程组
- 2 解二元一次方程组
- 3 二元一次方程组的应用
- 4 二元一次方程与一次函数
- *5 三元一次方程组
- 第八章 平行线的有关证明
- 1 定义与命题
- 2 证明的必要性
- 3 基本事实与定理
- 4 平行线的判定定理
- 5 平行线的性质定理
- 6 三角形内角和定理
- 第九章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
- 第十章 三角形的有关证明
- 1 全等三角形
- 2 等腰三角形
- 3 直角三角形
- 4 线段的垂直平分线
- 5 角平分线
- 第十一章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
