第八章 平行线的有关证明 章末复习 (含答案)
文档属性
| 名称 | 第八章 平行线的有关证明 章末复习 (含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 5.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-01-23 00:00:00 | ||
图片预览

文档简介
中小学教育资源及组卷应用平台
第八章 平行线的有关证明
章末复习
考点整合
考点一:命题
1.下列命题中,真命题是( )
A.锐角大于它的余角 B.锐角大于它的补角
C.钝角大于它的补角 D.锐角与钝角之和等于平角
2.下列句子中是命题的是( )
①三个角对应相等的两个三角形全等;②负数都小于0;③过直线l外一点作l的平行线;④如果a>b,a>c,那么b=c.
A.①② B.②③④ C.①②④ D.②④
3.能说明命题“如果两个角互补,那么这两个角一个是锐角,另一个是钝角”为假命题的两个角是( )
A.120°,60° B.75.1°,104.9° C.30°,60° D.90°,90°
4.命题“同位角相等,两直线平行”的条件是_______________________,结论是__________________________.
5.把定理“有两个角互余的三角形是直角三角形”写成“如果 那么 ”的形式:___________________________________________________________________.
考点二:平行线的判定
6.如图,下列推理正确的有( )
①因为∠1=∠4,所以BC∥AD;②因为∠2=∠3,所以AB∥CD;③因为∠BCD+∠ADC=180°,所以AD∥BC;④因为∠1+∠2+∠C=180°,所以BC∥AD.
A.1个 B.2个 C.3个 D.4个
7.下面是投影屏上出示的抢答题,需要回答横线上符号代表的内容,则回答正确的是( )
已知:如图,∠BEC=∠B+∠C.求证:AB∥CD.
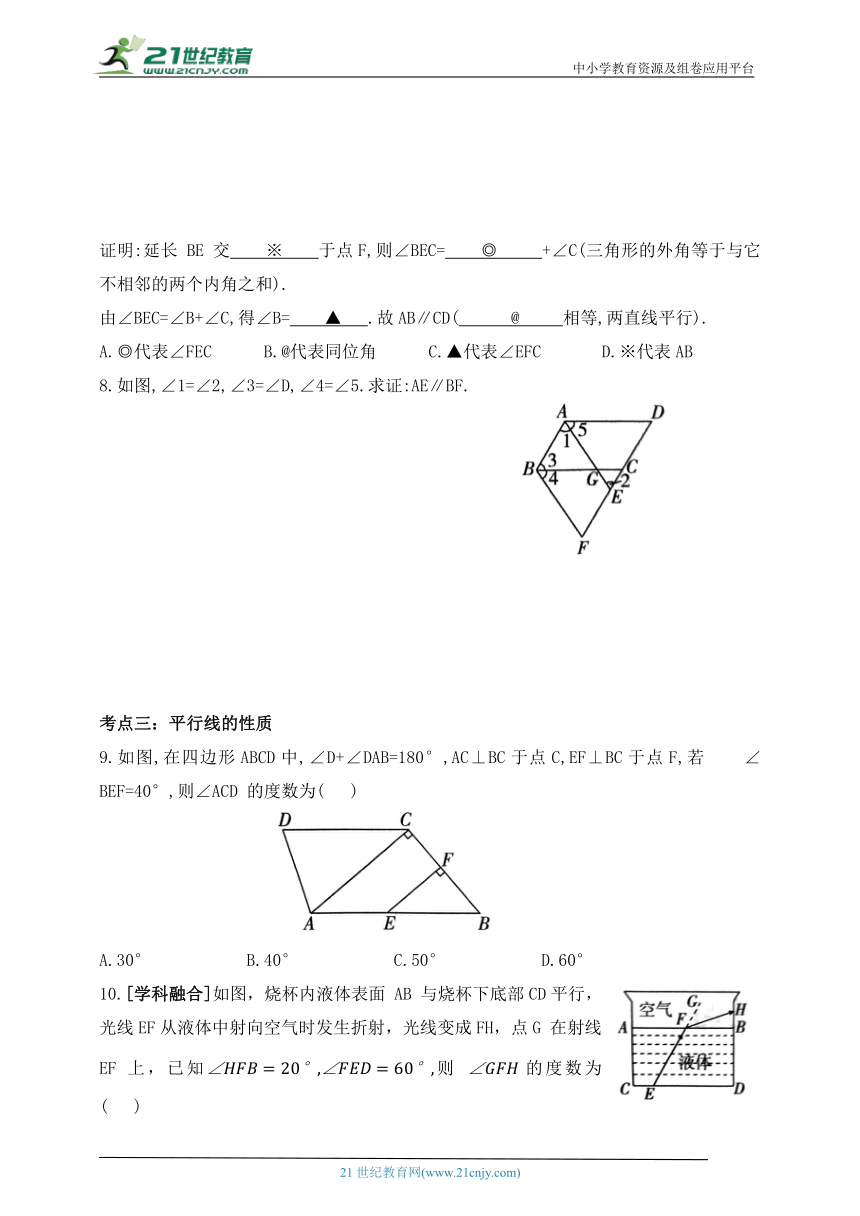
证明:延长 BE 交 ※ 于点F,则∠BEC= ◎ +∠C(三角形的外角等于与它不相邻的两个内角之和).
由∠BEC=∠B+∠C,得∠B= ▲ .故AB∥CD( @ 相等,两直线平行).
A.◎代表∠FEC B.@代表同位角 C.▲代表∠EFC D.※代表AB
8.如图,∠1=∠2,∠3=∠D,∠4=∠5.求证:AE∥BF.
考点三:平行线的性质
9.如图,在四边形ABCD中,∠D+∠DAB=180°,AC⊥BC于点C,EF⊥BC于点F,若 ∠BEF=40°,则∠ACD 的度数为( )
A.30° B.40° C.50° D.60°
10.[学科融合]如图,烧杯内液体表面 AB 与烧杯下底部CD平行,光线EF从液体中射向空气时发生折射,光线变成FH,点G 在射线EF 上,已知则 的度数为( )
A.20° B.40° C.60°
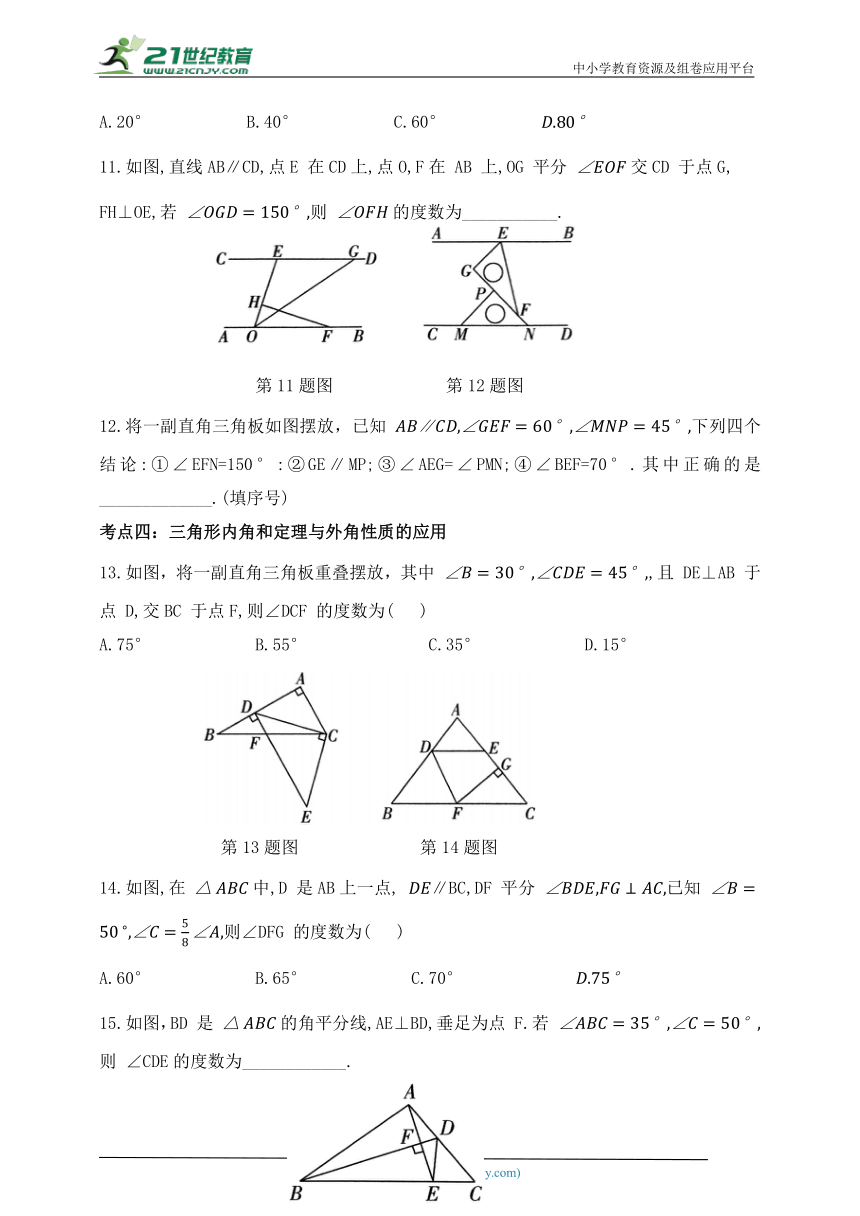
11.如图,直线AB∥CD,点E 在CD上,点O,F在 AB 上,OG 平分 交CD 于点G,
FH⊥OE,若 则 的度数为___________.
第11题图 第12题图
12.将一副直角三角板如图摆放,已知 ∥下列四个结论:①∠EFN=150°:②GE∥MP;③∠AEG=∠PMN;④∠BEF=70°.其中正确的是_____________.(填序号)
考点四:三角形内角和定理与外角性质的应用
13.如图,将一副直角三角板重叠摆放,其中 ,且 DE⊥AB 于点 D,交BC 于点F,则∠DCF 的度数为( )
A.75° B.55° C.35° D.15°
第13题图 第14题图
14.如图,在 中,D 是AB上一点, ∥BC,DF 平分 已知 则∠DFG 的度数为( )
A.60° B.65° C.70°
15.如图,BD 是 的角平分线,AE⊥BD,垂足为点 F.若 则 ∠CDE的度数为____________.
数学思想
思想一:方程思想
1.在△ABC 中, 则∠A,∠B,∠C 的度数分别为____________.
思想二:转化思想、整体思想
2.如图, 的度数为________________.
思想三:建模思想
3.如图,点 D,E 分别在AB,AC上, ∥F是AD上一点,FE 的延长线交BC 的延长线于点G.
(1)求证:
(2)求证:∠
参考答案
考点整合
1. C 2. C 3. D
4.两条直线被第三条直线所截,截得的同位角相等 这两条直线互相平行
5.如果一个三角形中有两个角互余,那么这个三角形是直角三角形
6. A 7. C
8.证明:∵∠1=∠2,∴AB∥DF,∴∠3=∠BCE.
又∵∠3=∠D,∴∠D=∠BCE,∴AD∥BC,∴∠AGB=∠5.
又∵∠4=∠5,∴∠4=∠AGB,∴AE∥BF.
9. B 10. B 11.30° 12.①②③ 13. D
14. D [解析]∵=180°,∴∠C=50°.
∵FG⊥AC,∴∠C+∠CFG=90°,∴∠CFG=40°.
∵DE∥BC,∴∠B+∠BDE=180°.
∵∠B = 50°,∴∠BDE = 130°.
∵ DF 平分∠BDE,
∥∠EDF= 65°.
∵∠BFD +∠DFG+∠CFG = 180°,∴∠DFG=75°.
15.45°
数学思想
1.55°,25°,100°
2.360°[解析]如图,
由三角形的内角和定理,得∠A+∠B +∠1=180°①,
∠C+∠D+∠3=180°②,
∠E+∠F+∠2=180°③.
∵∠1=∠4,∠2=∠5,∠3=∠6,且∠4+∠5+∠6=180°,∴∠1+∠2+∠3=180°④.
由①+②+③-④,得∠A+∠B+∠C+∠D+∠E+∠F=360°.
3.证明:(1)∵∠EGH 是△FBG 的外角,∴∠EGH>∠B.
又∵DE∥BC,∴∠B=∠ADE,∴∠EGH>∠ADE.
(2)∵∠BFE 是△AFE 的外角,∴∠BFE =∠A +∠AEF.
∵∠EGH 是△BFG 的外角,∴∠EGH=∠B+∠BFE,∴∠EGH=∠B+∠A+∠AEF.
又∵DE∥BC,∴∠B=∠ADE,∴∠EGH=∠ADE+∠A+∠AEF.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
第八章 平行线的有关证明
章末复习
考点整合
考点一:命题
1.下列命题中,真命题是( )
A.锐角大于它的余角 B.锐角大于它的补角
C.钝角大于它的补角 D.锐角与钝角之和等于平角
2.下列句子中是命题的是( )
①三个角对应相等的两个三角形全等;②负数都小于0;③过直线l外一点作l的平行线;④如果a>b,a>c,那么b=c.
A.①② B.②③④ C.①②④ D.②④
3.能说明命题“如果两个角互补,那么这两个角一个是锐角,另一个是钝角”为假命题的两个角是( )
A.120°,60° B.75.1°,104.9° C.30°,60° D.90°,90°
4.命题“同位角相等,两直线平行”的条件是_______________________,结论是__________________________.
5.把定理“有两个角互余的三角形是直角三角形”写成“如果 那么 ”的形式:___________________________________________________________________.
考点二:平行线的判定
6.如图,下列推理正确的有( )
①因为∠1=∠4,所以BC∥AD;②因为∠2=∠3,所以AB∥CD;③因为∠BCD+∠ADC=180°,所以AD∥BC;④因为∠1+∠2+∠C=180°,所以BC∥AD.
A.1个 B.2个 C.3个 D.4个
7.下面是投影屏上出示的抢答题,需要回答横线上符号代表的内容,则回答正确的是( )
已知:如图,∠BEC=∠B+∠C.求证:AB∥CD.
证明:延长 BE 交 ※ 于点F,则∠BEC= ◎ +∠C(三角形的外角等于与它不相邻的两个内角之和).
由∠BEC=∠B+∠C,得∠B= ▲ .故AB∥CD( @ 相等,两直线平行).
A.◎代表∠FEC B.@代表同位角 C.▲代表∠EFC D.※代表AB
8.如图,∠1=∠2,∠3=∠D,∠4=∠5.求证:AE∥BF.
考点三:平行线的性质
9.如图,在四边形ABCD中,∠D+∠DAB=180°,AC⊥BC于点C,EF⊥BC于点F,若 ∠BEF=40°,则∠ACD 的度数为( )
A.30° B.40° C.50° D.60°
10.[学科融合]如图,烧杯内液体表面 AB 与烧杯下底部CD平行,光线EF从液体中射向空气时发生折射,光线变成FH,点G 在射线EF 上,已知则 的度数为( )
A.20° B.40° C.60°
11.如图,直线AB∥CD,点E 在CD上,点O,F在 AB 上,OG 平分 交CD 于点G,
FH⊥OE,若 则 的度数为___________.
第11题图 第12题图
12.将一副直角三角板如图摆放,已知 ∥下列四个结论:①∠EFN=150°:②GE∥MP;③∠AEG=∠PMN;④∠BEF=70°.其中正确的是_____________.(填序号)
考点四:三角形内角和定理与外角性质的应用
13.如图,将一副直角三角板重叠摆放,其中 ,且 DE⊥AB 于点 D,交BC 于点F,则∠DCF 的度数为( )
A.75° B.55° C.35° D.15°
第13题图 第14题图
14.如图,在 中,D 是AB上一点, ∥BC,DF 平分 已知 则∠DFG 的度数为( )
A.60° B.65° C.70°
15.如图,BD 是 的角平分线,AE⊥BD,垂足为点 F.若 则 ∠CDE的度数为____________.
数学思想
思想一:方程思想
1.在△ABC 中, 则∠A,∠B,∠C 的度数分别为____________.
思想二:转化思想、整体思想
2.如图, 的度数为________________.
思想三:建模思想
3.如图,点 D,E 分别在AB,AC上, ∥F是AD上一点,FE 的延长线交BC 的延长线于点G.
(1)求证:
(2)求证:∠
参考答案
考点整合
1. C 2. C 3. D
4.两条直线被第三条直线所截,截得的同位角相等 这两条直线互相平行
5.如果一个三角形中有两个角互余,那么这个三角形是直角三角形
6. A 7. C
8.证明:∵∠1=∠2,∴AB∥DF,∴∠3=∠BCE.
又∵∠3=∠D,∴∠D=∠BCE,∴AD∥BC,∴∠AGB=∠5.
又∵∠4=∠5,∴∠4=∠AGB,∴AE∥BF.
9. B 10. B 11.30° 12.①②③ 13. D
14. D [解析]∵=180°,∴∠C=50°.
∵FG⊥AC,∴∠C+∠CFG=90°,∴∠CFG=40°.
∵DE∥BC,∴∠B+∠BDE=180°.
∵∠B = 50°,∴∠BDE = 130°.
∵ DF 平分∠BDE,
∥∠EDF= 65°.
∵∠BFD +∠DFG+∠CFG = 180°,∴∠DFG=75°.
15.45°
数学思想
1.55°,25°,100°
2.360°[解析]如图,
由三角形的内角和定理,得∠A+∠B +∠1=180°①,
∠C+∠D+∠3=180°②,
∠E+∠F+∠2=180°③.
∵∠1=∠4,∠2=∠5,∠3=∠6,且∠4+∠5+∠6=180°,∴∠1+∠2+∠3=180°④.
由①+②+③-④,得∠A+∠B+∠C+∠D+∠E+∠F=360°.
3.证明:(1)∵∠EGH 是△FBG 的外角,∴∠EGH>∠B.
又∵DE∥BC,∴∠B=∠ADE,∴∠EGH>∠ADE.
(2)∵∠BFE 是△AFE 的外角,∴∠BFE =∠A +∠AEF.
∵∠EGH 是△BFG 的外角,∴∠EGH=∠B+∠BFE,∴∠EGH=∠B+∠A+∠AEF.
又∵DE∥BC,∴∠B=∠ADE,∴∠EGH=∠ADE+∠A+∠AEF.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
- 第七章 二元一次方程组
- 1 二元一次方程组
- 2 解二元一次方程组
- 3 二元一次方程组的应用
- 4 二元一次方程与一次函数
- *5 三元一次方程组
- 第八章 平行线的有关证明
- 1 定义与命题
- 2 证明的必要性
- 3 基本事实与定理
- 4 平行线的判定定理
- 5 平行线的性质定理
- 6 三角形内角和定理
- 第九章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
- 第十章 三角形的有关证明
- 1 全等三角形
- 2 等腰三角形
- 3 直角三角形
- 4 线段的垂直平分线
- 5 角平分线
- 第十一章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
