第八章 平行线的有关证明 专项训练 新考向——综合与实践(含答案)
文档属性
| 名称 | 第八章 平行线的有关证明 专项训练 新考向——综合与实践(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 3.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-01-23 21:40:35 | ||
图片预览

文档简介
中小学教育资源及组卷应用平台
第八章 平行线的有关证明
专项训练 新考向——综合与实践
1.综合与实践
【问题情境】数学课上,老师出了这样一道题:如图①,∥CD,点 E 在直线AB,CD 之间.求证:
【探究证明】同学们把这种图形戏称“猪脚型”,勤奋小组和快乐小组给出了两种不同的证明过程.
勤奋小组
证明:如图②,过点 E 作 ∥则
∥∥(依据:____________________________),
快乐小组
证明:如图③,延长AE 交CD 于点G,
(1)勤奋小组证明过程中的“依据”是__________________________________.
(2)补全快乐小组的证明过程.
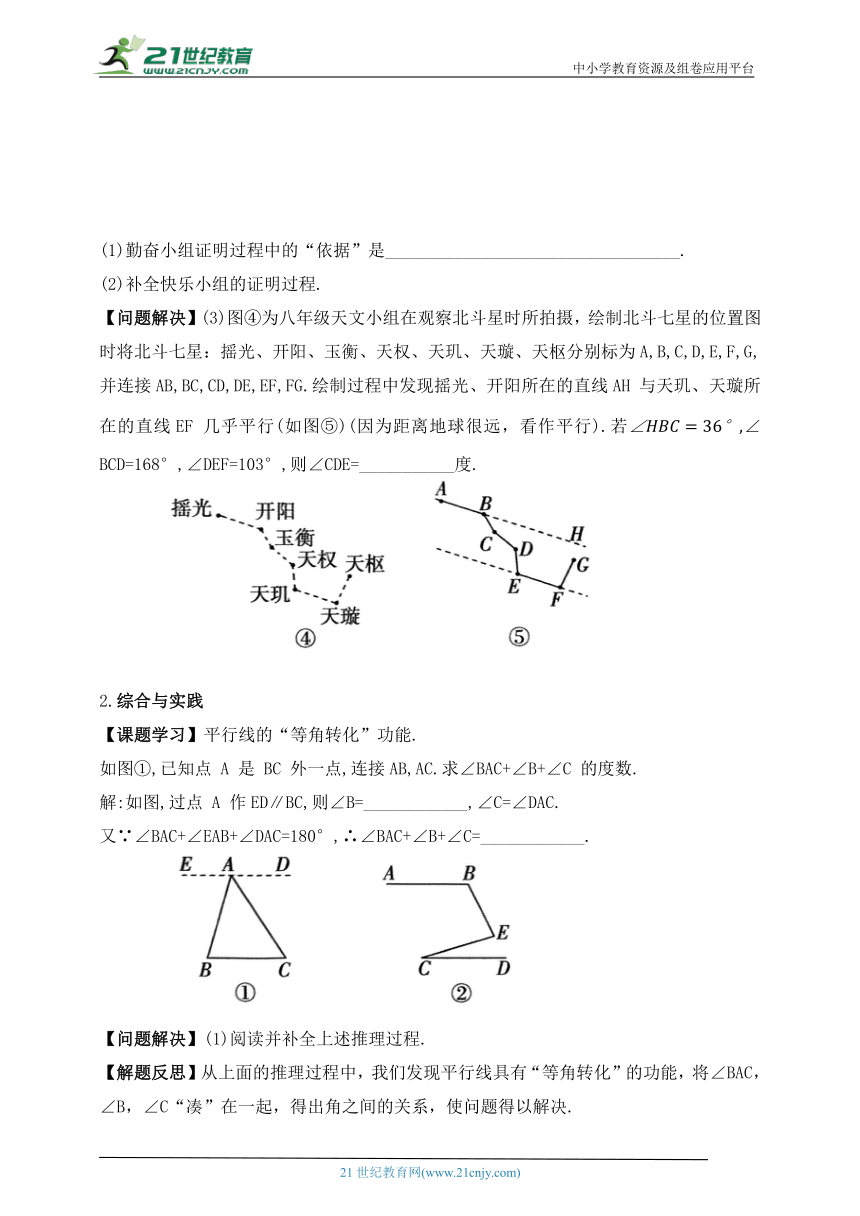
【问题解决】(3)图④为八年级天文小组在观察北斗星时所拍摄,绘制北斗七星的位置图时将北斗七星:摇光、开阳、玉衡、天权、天玑、天璇、天枢分别标为A,B,C,D,E,F,G,并连接AB,BC,CD,DE,EF,FG.绘制过程中发现摇光、开阳所在的直线AH 与天玑、天璇所在的直线EF 几乎平行(如图⑤)(因为距离地球很远,看作平行).若∠BCD=168°,∠DEF=103°,则∠CDE=___________度.
2.综合与实践
【课题学行线的“等角转化”功能.
如图①,已知点 A 是 BC 外一点,连接AB,AC.求∠BAC+∠B+∠C 的度数.
解:如图,过点 A 作ED∥BC,则∠B=____________,∠C=∠DAC.
又∵∠BAC+∠EAB+∠DAC=180°,∴∠BAC+∠B+∠C=____________.
【问题解决】(1)阅读并补全上述推理过程.
【解题反思】从上面的推理过程中,我们发现平行线具有“等角转化”的功能,将∠BAC,∠B,∠C“凑”在一起,得出角之间的关系,使问题得以解决.
【方法运用】(2)如图②,已知AB∥CD,BE,CE交于点E,若∠BEC=80°,则∠B- ∠C=______________.
【拓展探究】(3)如图③,已知AB∥CD,BF,CG分别平分∠ABE 和∠DCE,且BF,CG 所在直线交于点F,过点 F 作FH∥AB,若∠BFC=36°,则∠BEC=___________.
参考答案
1.解:(1)平行于同一条直线的两直线平行
(2)∵AB∥CD, ∴∠A=∠AGC.
∵∠AEC=∠C+∠AGC,∴∠AEC=∠A+∠C. (3)127
2.解:(1)∠EAB 180° (2)100°
[解析]如图,过点 E 作EF∥AB.
∵AB∥CD,∴CD∥EF,∴∠FEC=∠C.
∵AB∥EF,∴∠B+∠BEF=180°,∴∠BEF=180°-∠B.
∵∠BEC=80°,∴∠FEC+∠BEF=80°,∴∠C+180°-∠B=80°,
∴∠B-∠C=180°-80°=100°.
(3)108° [解析]如图,过点 E 作EM∥AB.
∵AB∥CD,∴EM∥CD,∴∠MEC =∠DCE.
∵CG 平分∠DCE,∴∠ECG=∠DCG.设∠ECG=∠DCG=α,则∠DCE=2α,∴∠MEC=2α.
∵AB∥CD,FH∥AB,∴CD∥FH,∴∠HFC=∠DCG=α.
∵∠BFC=36°,∴∠BFH =∠BFC+∠HFC=36°+α.
∵FH∥AB,∴∠ABF=∠BFH=36°+α.
∵BF平分∠ABE,∴∠ABE=2∠ABF=2×(36°+α)=72°+2α.
∵EM∥AB,∴∠ABE+∠BEM=180°,∴∠BEM=180°-∠ABE=180°-(72°+2α)=108°-2α,∴∠BEC=∠BEM+∠MEC=108°-2α+2α=108°.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
第八章 平行线的有关证明
专项训练 新考向——综合与实践
1.综合与实践
【问题情境】数学课上,老师出了这样一道题:如图①,∥CD,点 E 在直线AB,CD 之间.求证:
【探究证明】同学们把这种图形戏称“猪脚型”,勤奋小组和快乐小组给出了两种不同的证明过程.
勤奋小组
证明:如图②,过点 E 作 ∥则
∥∥(依据:____________________________),
快乐小组
证明:如图③,延长AE 交CD 于点G,
(1)勤奋小组证明过程中的“依据”是__________________________________.
(2)补全快乐小组的证明过程.
【问题解决】(3)图④为八年级天文小组在观察北斗星时所拍摄,绘制北斗七星的位置图时将北斗七星:摇光、开阳、玉衡、天权、天玑、天璇、天枢分别标为A,B,C,D,E,F,G,并连接AB,BC,CD,DE,EF,FG.绘制过程中发现摇光、开阳所在的直线AH 与天玑、天璇所在的直线EF 几乎平行(如图⑤)(因为距离地球很远,看作平行).若∠BCD=168°,∠DEF=103°,则∠CDE=___________度.
2.综合与实践
【课题学行线的“等角转化”功能.
如图①,已知点 A 是 BC 外一点,连接AB,AC.求∠BAC+∠B+∠C 的度数.
解:如图,过点 A 作ED∥BC,则∠B=____________,∠C=∠DAC.
又∵∠BAC+∠EAB+∠DAC=180°,∴∠BAC+∠B+∠C=____________.
【问题解决】(1)阅读并补全上述推理过程.
【解题反思】从上面的推理过程中,我们发现平行线具有“等角转化”的功能,将∠BAC,∠B,∠C“凑”在一起,得出角之间的关系,使问题得以解决.
【方法运用】(2)如图②,已知AB∥CD,BE,CE交于点E,若∠BEC=80°,则∠B- ∠C=______________.
【拓展探究】(3)如图③,已知AB∥CD,BF,CG分别平分∠ABE 和∠DCE,且BF,CG 所在直线交于点F,过点 F 作FH∥AB,若∠BFC=36°,则∠BEC=___________.
参考答案
1.解:(1)平行于同一条直线的两直线平行
(2)∵AB∥CD, ∴∠A=∠AGC.
∵∠AEC=∠C+∠AGC,∴∠AEC=∠A+∠C. (3)127
2.解:(1)∠EAB 180° (2)100°
[解析]如图,过点 E 作EF∥AB.
∵AB∥CD,∴CD∥EF,∴∠FEC=∠C.
∵AB∥EF,∴∠B+∠BEF=180°,∴∠BEF=180°-∠B.
∵∠BEC=80°,∴∠FEC+∠BEF=80°,∴∠C+180°-∠B=80°,
∴∠B-∠C=180°-80°=100°.
(3)108° [解析]如图,过点 E 作EM∥AB.
∵AB∥CD,∴EM∥CD,∴∠MEC =∠DCE.
∵CG 平分∠DCE,∴∠ECG=∠DCG.设∠ECG=∠DCG=α,则∠DCE=2α,∴∠MEC=2α.
∵AB∥CD,FH∥AB,∴CD∥FH,∴∠HFC=∠DCG=α.
∵∠BFC=36°,∴∠BFH =∠BFC+∠HFC=36°+α.
∵FH∥AB,∴∠ABF=∠BFH=36°+α.
∵BF平分∠ABE,∴∠ABE=2∠ABF=2×(36°+α)=72°+2α.
∵EM∥AB,∴∠ABE+∠BEM=180°,∴∠BEM=180°-∠ABE=180°-(72°+2α)=108°-2α,∴∠BEC=∠BEM+∠MEC=108°-2α+2α=108°.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
- 第七章 二元一次方程组
- 1 二元一次方程组
- 2 解二元一次方程组
- 3 二元一次方程组的应用
- 4 二元一次方程与一次函数
- *5 三元一次方程组
- 第八章 平行线的有关证明
- 1 定义与命题
- 2 证明的必要性
- 3 基本事实与定理
- 4 平行线的判定定理
- 5 平行线的性质定理
- 6 三角形内角和定理
- 第九章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
- 第十章 三角形的有关证明
- 1 全等三角形
- 2 等腰三角形
- 3 直角三角形
- 4 线段的垂直平分线
- 5 角平分线
- 第十一章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
