对数函数的图像和性质
图片预览





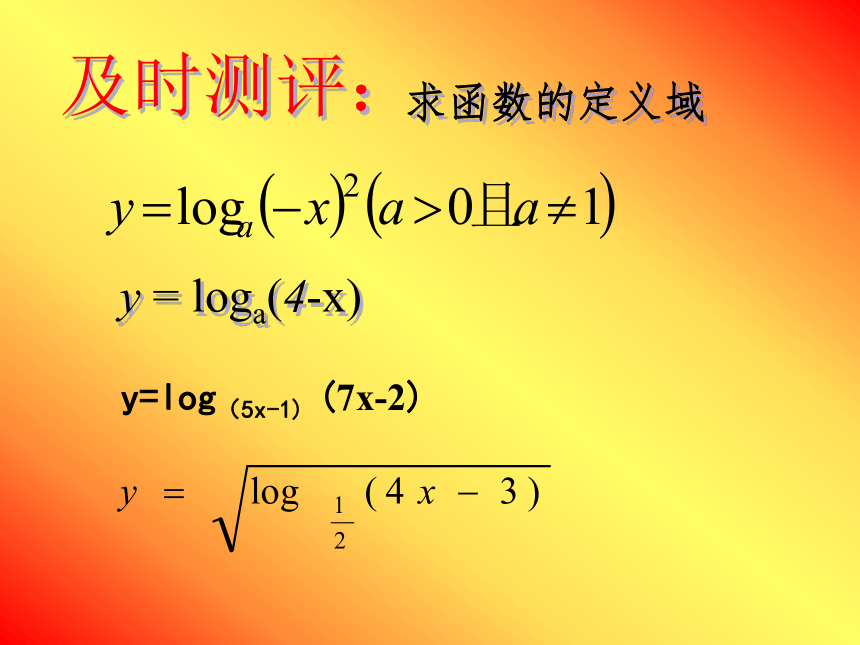
文档简介
课件14张PPT。 ⒈指数函数与对数函数是什么关系?
⒋要完成对数函数的图像和性质的推导都应该掌握哪些知识点,这些知识点你掌握了吗? ⒉能否用指数函数的性质来推导对数函数的性质? ⒊推导的依据是什么?反函数的性质在直角坐标系中会画出指数函数的图像指数函数的性质
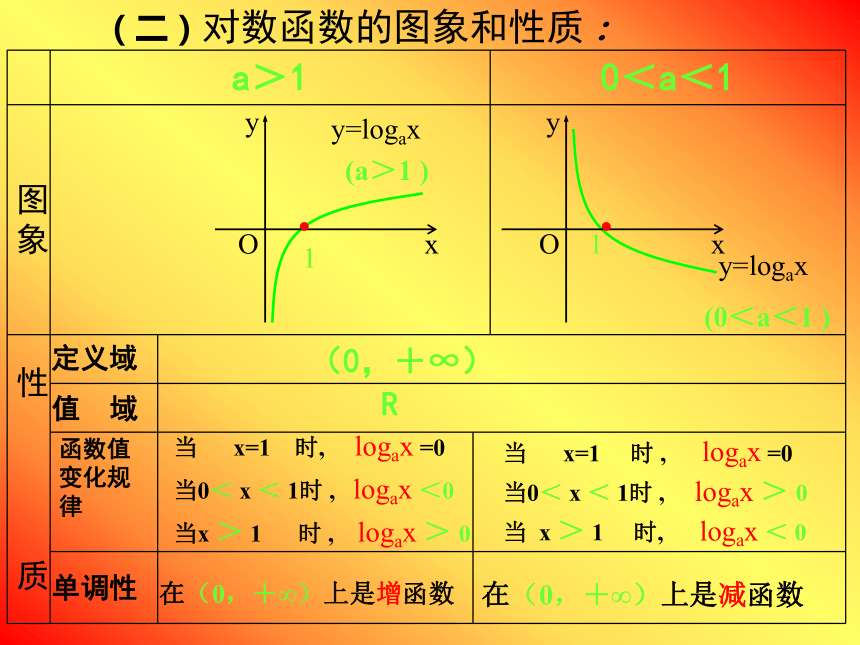
对数函数的图形和性质(二)对数函数的图象和性质:定义域R当 x=1 时, logax =0
当0< x < 1时 , logax <0
当x > 1 时 , logax > 0在(0,+∞)上是增函数在(0,+∞)上是减函数(0,+∞)值 域1y=logax
(a>1 )1y=logax
(0<a<1 )函数值变化规律当 x=1 时 , logax =0
当0< x < 1时 , logax > 0
当 x > 1 时, logax < 0单调性··例1.求下列函数的定义域:(1)y=log5x2(2) y=loga(4-x)你认为例1的解题思路是什么?真数必须大于零,即N>0。如果真数是由复合函数组成,求定义域时要注意组成复合函数的各部分都要有意义。及时测评: y = loga(4-x)y=log(5x-1) (7x-2)求函数的定义域例2:求下列函数恒过那些定点?⑴ y=logax⑵ y=logax-1解:⑴因为loga1=0,所以函数过﹙1,0﹚解:⑵因为当x=2时y=0,所以函数
y=logax-1恒过﹙2,0﹚你是怎样理解例2题的解题思路?对数函数恒过﹙1,0﹚如果真数N是由复合函数组成,求对数函数恒过定点时,只需让真数N整体等于1求出x的值。即过﹙x,0﹚及时测评:①函数y= logax恒过定点﹙﹚②恒过定点﹙﹚③恒过定点﹙﹚④ y=loga(4a-x) 恒过﹙4,2﹚,求a的值求下列函数恒过点的坐标
1、本节课你都学习了那些知识?
2、通过本节课的学习,你都掌握了那些做题技巧?
课 堂 小 结作 业1、熟记对数函数
的图象和性质
2、P97.习题3-5.3 5谢谢指导 课件设计与制作:姜永刚铜川市第二中学
⒋要完成对数函数的图像和性质的推导都应该掌握哪些知识点,这些知识点你掌握了吗? ⒉能否用指数函数的性质来推导对数函数的性质? ⒊推导的依据是什么?反函数的性质在直角坐标系中会画出指数函数的图像指数函数的性质
对数函数的图形和性质(二)对数函数的图象和性质:定义域R当 x=1 时, logax =0
当0< x < 1时 , logax <0
当x > 1 时 , logax > 0在(0,+∞)上是增函数在(0,+∞)上是减函数(0,+∞)值 域1y=logax
(a>1 )1y=logax
(0<a<1 )函数值变化规律当 x=1 时 , logax =0
当0< x < 1时 , logax > 0
当 x > 1 时, logax < 0单调性··例1.求下列函数的定义域:(1)y=log5x2(2) y=loga(4-x)你认为例1的解题思路是什么?真数必须大于零,即N>0。如果真数是由复合函数组成,求定义域时要注意组成复合函数的各部分都要有意义。及时测评: y = loga(4-x)y=log(5x-1) (7x-2)求函数的定义域例2:求下列函数恒过那些定点?⑴ y=logax⑵ y=logax-1解:⑴因为loga1=0,所以函数过﹙1,0﹚解:⑵因为当x=2时y=0,所以函数
y=logax-1恒过﹙2,0﹚你是怎样理解例2题的解题思路?对数函数恒过﹙1,0﹚如果真数N是由复合函数组成,求对数函数恒过定点时,只需让真数N整体等于1求出x的值。即过﹙x,0﹚及时测评:①函数y= logax恒过定点﹙﹚②恒过定点﹙﹚③恒过定点﹙﹚④ y=loga(4a-x) 恒过﹙4,2﹚,求a的值求下列函数恒过点的坐标
1、本节课你都学习了那些知识?
2、通过本节课的学习,你都掌握了那些做题技巧?
课 堂 小 结作 业1、熟记对数函数
的图象和性质
2、P97.习题3-5.3 5谢谢指导 课件设计与制作:姜永刚铜川市第二中学
