2024-2025学年五年级数学上册寒假巩固练习(北师大版)第4练- 多边形的面积 (含答案+解析)
文档属性
| 名称 | 2024-2025学年五年级数学上册寒假巩固练习(北师大版)第4练- 多边形的面积 (含答案+解析) |  | |
| 格式 | docx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-01-24 12:39:37 | ||
图片预览

文档简介
2024-2025学年五年级数学上册寒假巩固练习(北师大版)
第4练- 多边形的面积
一、认真填空。
1.我国古代数学家刘徽利用“出入相补”原理计算梯形面积。如图,转化后的平行四边形的底是10cm,高是hcm,原梯形的高是 cm,面积是 cm2。
2.如图,数一数有 个平行四边形, 个梯形。
3.如图,已知直角三角形 ABC 的面积是18cm2,则BC的长度是 cm。
4.有一种船的船帆是三角形的,称为“三角帆”,它可以助力船逆风行进(如下图)。三角形船帆的底大约是5m,高大约是12m,这个三角形船帆的面积大约是 m2。
5. 如图,梯形ABCD的面积为22平方米,点E在BC上,三角形ADE的面积是三角形ABE面积的2倍,那么三角形DEC的面积为 平方米。
6.535cm2= dm 21.5公顷= 平方千米 2.5t= kg
3.05m2= m2 dm 3元零9分= 元
7.一个三角形的底是10厘米,高是底的,它的面积是 cm2;与它等底等高平行四边形的面积是 cm2。
8. 甜甜将一张面积为45平方厘米的梯形纸片按下面方式剪开后拼成了一个平行四边形,则所拼成的平行四边形长边所对应的高为 厘米。
9.观察图形并填空。(每个小方格的面积表示1平方厘米),灯笼的面积约是 平方厘米,小帆船的面积约是 平方厘米。
二、仔细判断。
10.平行四边形的高有无数条,直角三角形的高只有一条。( )
11.用梯形的面积计算公式S梯=(上底+下底)×高÷2也可以计算三角形的面积,只要把梯形的上底看作0即可。( )
12. 若平行四边形与三角形等底等高,则它们的面积必定相等。( )
13. 左边这四个图形都是梯形。( )
14.用梯形面积计算公式可以计算平行四边形和三角形的面积。( )
三、精心选择。
15.如图,能求出三角形面积的算式是( )。
A.bh÷2 B.ch÷2 C.ah÷2 D.ab÷2
16. 一个三角形和平行四边形等底等高,平行四边形的面积是8cm2,则三角形的面积是( )。
A.8cm2 B.4cm2 C.16cm2 D.2cm2
17. 下面是四个完全相同的长方形,其中阴影部分的面积相等的是 ( )。
A.①②③④ B.①②③ C.①③ D.①②
18. 把一个平行四边形沿着它的一条高剪成两部分后,拼成一个长方形,这个长方形和原来的平行四边形相比,下列结论正确的是( )。
A.周长不变,面积变了 B.周长不变,面积也不变
C.周长变了,面积不变 D.周长变了,面积也变了
19.将等腰三角形ABC沿虚线对折,折下来的部分恰好拼成了一个长方形(如下图),已知这个长方形的长是6cm,宽是4cm,三角形ABC的面积是( )cm2。
A.12 B.24 C.48 D.96
四、动手操作。
20.在下图方格纸上画一个三角形,一个平行四边形和一个梯形,并分别画出它们的一条高。
21. 如图,在平行四边形 ABCD中,BE∶EC=1∶2,点F是DC的中点,三角形ABE 的面积是10cm2,那么三角形ADF的面积是 cm2。
22.在方格图上分别画一个三角形、一个平行四边形和一个梯形,使它们的面积都与图中长方形的面积相等。
五、解决问题。
23.学校的三角形蔬菜种植园,其底是14m,高是9.2m,在劳动课上,学生计划给这块种植园施肥种植蔬菜,若种植园每平方米需要用60g肥料,则准备3.9kg肥料够吗
一块平行四边形广告牌的面积是 ,高是 1.8 m 。这条高对应的底边长是多少 m ?
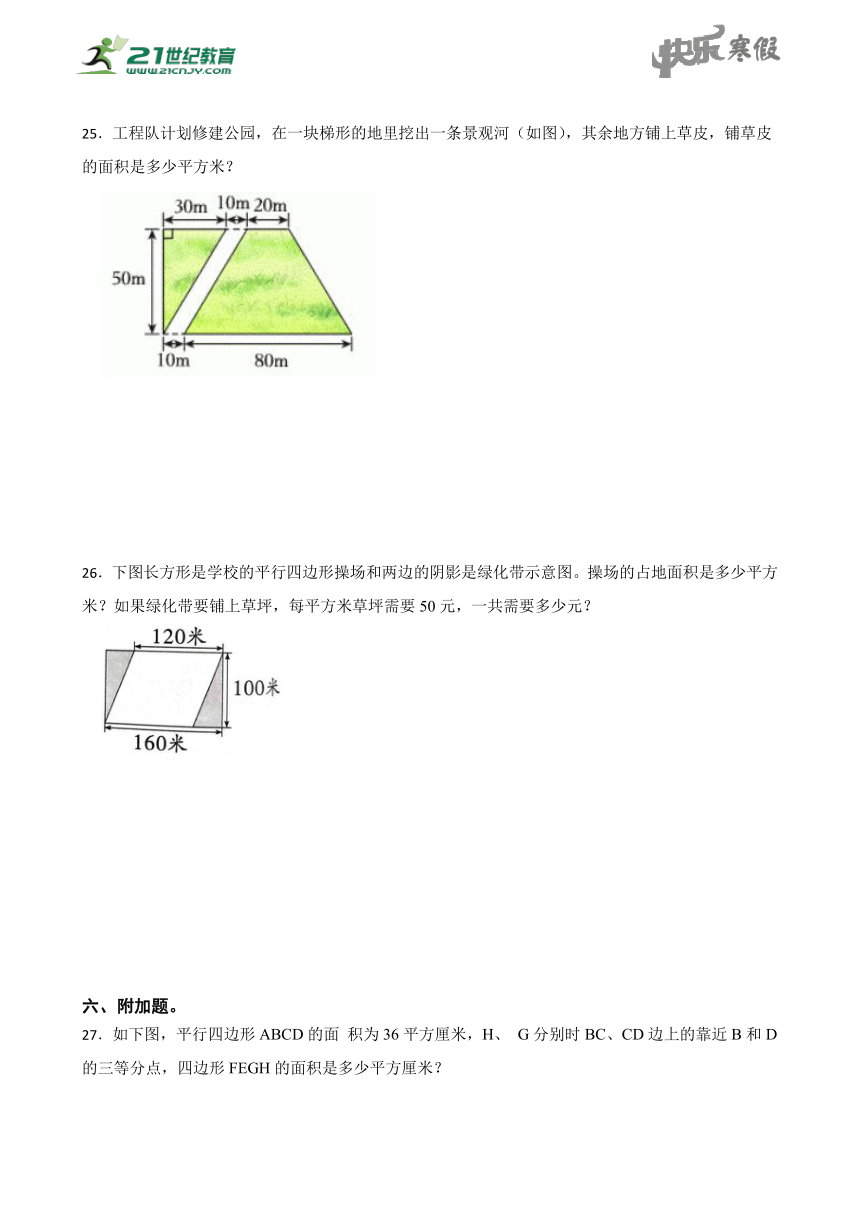
25.工程队计划修建公园,在一块梯形的地里挖出一条景观河(如图),其余地方铺上草皮,铺草皮的面积是多少平方米?
26.下图长方形是学校的平行四边形操场和两边的阴影是绿化带示意图。操场的占地面积是多少平方米?如果绿化带要铺上草坪,每平方米草坪需要50元,一共需要多少元?
六、附加题。
27.如下图,平行四边形ABCD的面 积为36平方厘米,H、 G分别时BC、CD边上的靠近B和D的三等分点,四边形FEGH的面积是多少平方厘米?
答案解析部分
1.2h;10h
解:原梯形的高是平行四边形高的2倍,是2h厘米;
梯形拼成平行四边形,面积不变,面积是10h平方厘米。
故答案为:2h;10h。
平行四边形面积=平行四边形的底×平行四边形的高。
2.2;4
解:由2个图形组成的平行四边形有2个;
由2个图形组成的梯形有1个,由3个图形组成的梯形有2个,由4个图形组成的梯形有1个,共4个梯形。
故答案为:2;4。
两组对边分别平行的四边形叫做平行四边形;一组对边平行而另一组对边不平行的四边形是梯形;据此解答。
3.9
解:
解这个方程,得到:
进一步解得:
因此,BC的长度是。
故答案为:9
根据题目给定的直角三角形面积公式 和给定的数据,高,可以将已知值代入面积公式中求解底边 的长度。
4.30
解:5×12÷2
=60÷2
=30(平方米)。
故答案为:30。
这个三角形船帆的面积大约=底×高÷2。
5.10
解:因为三角形ADE的面积是三角形ABE面积的2倍,
因为三角形ABE与三角形ADE等高,
所以AD是BE的2倍,
所以AD的长为4米,
梯形ABCD的高为22×2÷(2+5+4)=4(米),
即三角形DEC的面积为5×4÷2=10(平方米)。
故答案为:10。
根据三角形ADE与三角形ABE面积关系,推知AD与BE长度的关系,求出AD的长;已知梯形的面积、上底和下底,根据梯形面积=(上底+下底)×高÷2,求出高AE的长度;用三角形DEC的底边CE乘以高AE除以2得到三角形的面积。
6.5.35;0.215;2500;3;5;3.09
解:535cm2=5.35dm2;21.5公顷=0.215平方千米;2.5t=2500kg;
3.05m2=3m25dm2;3元零9分=3.09元。
故答案为:5.35;0.215;2500;3;5;3.09。
1dm2=100cm2;1平方千米=100公顷;1t=1000kg;
1m2=100dm2;1元=100分;
低级单位的量化高级单位除以进率;高级单位的量化低级单位乘进率。
7.10;20
解:10× ×10÷2
=20÷2
=10(平方厘米)
10×2=20(平方厘米)。
故答案为:10;20。
这个三角形的面积=底×高÷2,其中,高=底×;与它等底等高平行四边形的面积=这个三角形的面积×2。
8.3
解:45×2÷(5+10)=90÷15=6(cm)
6÷2=3(cm)
故答案为:3。
已知梯形的上底、下底和面积,可以求出梯形的高;剪开后两纸片可以组成一个平行四边形,说明梯形ADEF和梯形EFBC的高相等,均为原梯形ABCD高的一半,同时也是所拼成的平行四边形长边所对应的高。
9.14;15
解:灯笼的面积:满格有7个,不满格有14个;
7+14÷2
=7+7
=14(个)
1×14=14(平方厘米)
小帆船的面积:
(8+4)×2÷2+2×3÷2
=12×2÷2+6÷2
=12+3
=15(平方厘米)。
故答案为:14;15。
计算不规则图形的面积,可以数格子,分别数出满格和不满格的数量,不满格的数量按半格计算,再加上满格的数量,就是灯笼的格子数,最后乘每个小方格的面积即可。
小帆船的面积=梯形的面积+三角形的面积,其中,梯形的面积=(上底+下底)×高÷2,三角形的面积=底×高÷2。
10.错误
解:平行四边形的高有无数条,直角三角形的高有三条。原题说法错误。
故答案为:错误。
三角形都有三条高;锐角三角形的三条高都在三角形的内部;直角三角形的两条高分别在两条直角边上,另一条高在三角形的内部;钝角三角形的钝角的两边上的高在三角形外部,另一条高在三角形的内部。
11.正确
解:用梯形的面积计算公式S梯=(上底+下底)×高÷2也可以计算三角形的面积,只要把梯形的上底看作0即可。说法正确。
故答案为:正确。
梯形的上底看作0,形状就变成了三角形,梯形的下底就是三角形的底边。
12.错误
解:若平行四边形与三角形等底等高,则平行四边形面积是三角形面积的2倍,原题说法错误。
故答案为:错误。
平行四边形面积=底×高,三角形面积=底×高÷2,据此判断。
13.错误
解:第一个、第二个和第四个图形是只有一组对边平行的四边形,所以是梯形;第三个图形是两组对边都不平行的四边形,不是梯形。
故答案为:错误。
根据只有一组对边平行的四边形叫做梯形进行判断即可。
14.正确
解:用两个完全一样的梯形可以拼成平行四边形,这个平行四边形的面积=梯形的面积×2;
平行四边形又可以切成两个完全一样的三角形,所以用梯形面积计算公式可以计算平行四边形和三角形的面积。
故答案为:正确。
用两个完全一样的梯形可以拼成平行四边形,用两个完全一样的三角形可以拼成平行四边形,据此计算。
15.B
解:三角形的面积是ad÷2或者ch÷2。
故答案为:B。
三角形的面积=底×高÷2,其中,底a上的高是d,底c上的高是h。
16.B
解:8÷2=4(平方厘米)。
故答案为:B。
三角形的面积=等底等高的平行四边形的面积÷2。
17.A
解:①的面积=②的面积=③的面积=④的面积。
故答案为:A。
三角形的面积=底×高÷2,等底等高的三角形面积相等。
18.C
解:如图,把一个平行四边形沿高剪拼成一个长方形,底和高都不变,则面积不变,但是平行四边形边的长度总和变小了,所以周长变小了。
故答案为:C。
根据题目给出条件作出图像,平行四边形的底边变成了长方形的长,没有变化,斜边变成了长方形的宽,比原来变短了,可知周长变短了;平行四边形面积=底×高,长方形面积=宽×长,可知面积没有变化。
19.C
解:6×4×2=48(平方厘米)
故答案为:C。
看图可知,三角形ABC的面积是拼成长方形面积的2倍,因此用长方形面积乘2即可求出三角形ABC的面积。
20.
由三条线段围成的封闭图形叫三角形;
平行四边形的对边平行且相等;
梯形只有一组对边平行;
三角形作高的方法:①把三角尺的一条直角边与已知底重合;②沿着底移动三角尺,使三角尺的另一条直角边通过这条底对面的顶点,沿这条直角边画一条直线,顶点与垂足之间的线段就是这个三角形的高;③在垂足处标出垂直符号;
平行四边形作高的方法:过平行四边形的一组对边上的一点向对边画垂线,这点与垂足之间的线段是平行四边形的高;
梯形作高的方法:过梯形的上底上的任意一点向下底画垂线,这点与垂足之间的线段是梯形的高,据此作图。
21.15
解:如图,连结AC
∵E在BC上,BE:EC = 1:2
∴S△ABE:S△ABC=BE:BC = 1:3
∴S△ABC
∵AC是平行四边形ABCD的对角线
∴S△ABC=S△ACD
∵F是CD的中点
∴S△AFD:S△ADC= DF:CD = 1:2
∴S△AFD=
答: 三角形ADF的面积是15cm2
故答案为:15
连接AC,则三角形ABC的面积等于三角形ADC的面积。 因为 BE∶EC=1∶2,则三角形ABE的面积:三角形ABC面积等于1:3
三角形ABC的面积 三角形ADF 的面积是三角形ADC的面积的一半,即
22.解:长方形面积=3×2=6;三角形底画6格,高画2格,三角形面积=6×2÷2=6;
平行四边形底画3格,高画2格,平行四边形面积=3×2=6;梯形的上底画2格,下底画4格,高画2格,梯形面积=(2+4)×2÷2=6;
长方形面积=长×宽,三角形面积=底×高÷2,平行四边形面积=底×高,梯形面积=(上底+下底)×高÷2。
23.解:根据题意,可得
答:准备3.9 kg肥料够。
根据三角形的面积公式:S=底×高÷2,求出蔬菜种植园的面积,然后再乘以每平方需要的化肥质量,然后再将克换算成千克,最后再跟3.9千克进行比较即可
24.解:7.2÷1.8=4(m)
答:这条高对应的底边长是4m。
平行四边形的面积=底×高,根据题意可得:平行四边形的面积÷高=这条高对应的底,据此解答即可。
25.解:[(30+20)+80]×50÷2
=[50+80]×50÷2
=130×50÷2
=6500÷2
=3250(平方米)
答:铺草皮的面积是3250平方米。
平移后铺草皮的面积合起来就是一个上底为(30+20)米,下底为80米,高为50米的梯形,梯形的面积=(上底+下底)×高÷2。
26.解:120×100=12000(平方米)
160×100-12000
=16000-12000
=4000(平方米)
4000×50=200000(元)
答:操场的占地面积是12000平方米;如果绿化带要铺上草坪,一共需要200000元。
观察图可知,操场的形状是平行四边形,要求操场的占地面积,应用公式:平行四边形的面积=底×高;绿化带的面积=大长方形的面积-操场的面积,然后用绿化带的面积×每平方米草坪的单价=铺草坪一共需要的总钱数。
27.解:连接 , 则.
而 (平方厘米)
所以 (平方厘米)
于是可得: E、F、o为BD的 4 等分点,
则 ( 平方厘米)
又因三角形 与三角形 是相似三角形, 且相似比为 , 则其面积比为 ,
所以 (平方厘米)
因此阴影部分的面积 (平方厘米)
答: 四边形EFGH的面积为7平方厘米。
关于平行四边形及其内部划分的面积计算问题。平行四边形ABCD的面积为36平方厘米,H和G分别是BC和CD边上的靠近B和D的三等分点,我们要找出四边形FEGH的面积。连接 后,找到各三角形与平行四边形面积之间的关系,通过比例和鸟头图形的性质进行计算。
第4练- 多边形的面积
一、认真填空。
1.我国古代数学家刘徽利用“出入相补”原理计算梯形面积。如图,转化后的平行四边形的底是10cm,高是hcm,原梯形的高是 cm,面积是 cm2。
2.如图,数一数有 个平行四边形, 个梯形。
3.如图,已知直角三角形 ABC 的面积是18cm2,则BC的长度是 cm。
4.有一种船的船帆是三角形的,称为“三角帆”,它可以助力船逆风行进(如下图)。三角形船帆的底大约是5m,高大约是12m,这个三角形船帆的面积大约是 m2。
5. 如图,梯形ABCD的面积为22平方米,点E在BC上,三角形ADE的面积是三角形ABE面积的2倍,那么三角形DEC的面积为 平方米。
6.535cm2= dm 21.5公顷= 平方千米 2.5t= kg
3.05m2= m2 dm 3元零9分= 元
7.一个三角形的底是10厘米,高是底的,它的面积是 cm2;与它等底等高平行四边形的面积是 cm2。
8. 甜甜将一张面积为45平方厘米的梯形纸片按下面方式剪开后拼成了一个平行四边形,则所拼成的平行四边形长边所对应的高为 厘米。
9.观察图形并填空。(每个小方格的面积表示1平方厘米),灯笼的面积约是 平方厘米,小帆船的面积约是 平方厘米。
二、仔细判断。
10.平行四边形的高有无数条,直角三角形的高只有一条。( )
11.用梯形的面积计算公式S梯=(上底+下底)×高÷2也可以计算三角形的面积,只要把梯形的上底看作0即可。( )
12. 若平行四边形与三角形等底等高,则它们的面积必定相等。( )
13. 左边这四个图形都是梯形。( )
14.用梯形面积计算公式可以计算平行四边形和三角形的面积。( )
三、精心选择。
15.如图,能求出三角形面积的算式是( )。
A.bh÷2 B.ch÷2 C.ah÷2 D.ab÷2
16. 一个三角形和平行四边形等底等高,平行四边形的面积是8cm2,则三角形的面积是( )。
A.8cm2 B.4cm2 C.16cm2 D.2cm2
17. 下面是四个完全相同的长方形,其中阴影部分的面积相等的是 ( )。
A.①②③④ B.①②③ C.①③ D.①②
18. 把一个平行四边形沿着它的一条高剪成两部分后,拼成一个长方形,这个长方形和原来的平行四边形相比,下列结论正确的是( )。
A.周长不变,面积变了 B.周长不变,面积也不变
C.周长变了,面积不变 D.周长变了,面积也变了
19.将等腰三角形ABC沿虚线对折,折下来的部分恰好拼成了一个长方形(如下图),已知这个长方形的长是6cm,宽是4cm,三角形ABC的面积是( )cm2。
A.12 B.24 C.48 D.96
四、动手操作。
20.在下图方格纸上画一个三角形,一个平行四边形和一个梯形,并分别画出它们的一条高。
21. 如图,在平行四边形 ABCD中,BE∶EC=1∶2,点F是DC的中点,三角形ABE 的面积是10cm2,那么三角形ADF的面积是 cm2。
22.在方格图上分别画一个三角形、一个平行四边形和一个梯形,使它们的面积都与图中长方形的面积相等。
五、解决问题。
23.学校的三角形蔬菜种植园,其底是14m,高是9.2m,在劳动课上,学生计划给这块种植园施肥种植蔬菜,若种植园每平方米需要用60g肥料,则准备3.9kg肥料够吗
一块平行四边形广告牌的面积是 ,高是 1.8 m 。这条高对应的底边长是多少 m ?
25.工程队计划修建公园,在一块梯形的地里挖出一条景观河(如图),其余地方铺上草皮,铺草皮的面积是多少平方米?
26.下图长方形是学校的平行四边形操场和两边的阴影是绿化带示意图。操场的占地面积是多少平方米?如果绿化带要铺上草坪,每平方米草坪需要50元,一共需要多少元?
六、附加题。
27.如下图,平行四边形ABCD的面 积为36平方厘米,H、 G分别时BC、CD边上的靠近B和D的三等分点,四边形FEGH的面积是多少平方厘米?
答案解析部分
1.2h;10h
解:原梯形的高是平行四边形高的2倍,是2h厘米;
梯形拼成平行四边形,面积不变,面积是10h平方厘米。
故答案为:2h;10h。
平行四边形面积=平行四边形的底×平行四边形的高。
2.2;4
解:由2个图形组成的平行四边形有2个;
由2个图形组成的梯形有1个,由3个图形组成的梯形有2个,由4个图形组成的梯形有1个,共4个梯形。
故答案为:2;4。
两组对边分别平行的四边形叫做平行四边形;一组对边平行而另一组对边不平行的四边形是梯形;据此解答。
3.9
解:
解这个方程,得到:
进一步解得:
因此,BC的长度是。
故答案为:9
根据题目给定的直角三角形面积公式 和给定的数据,高,可以将已知值代入面积公式中求解底边 的长度。
4.30
解:5×12÷2
=60÷2
=30(平方米)。
故答案为:30。
这个三角形船帆的面积大约=底×高÷2。
5.10
解:因为三角形ADE的面积是三角形ABE面积的2倍,
因为三角形ABE与三角形ADE等高,
所以AD是BE的2倍,
所以AD的长为4米,
梯形ABCD的高为22×2÷(2+5+4)=4(米),
即三角形DEC的面积为5×4÷2=10(平方米)。
故答案为:10。
根据三角形ADE与三角形ABE面积关系,推知AD与BE长度的关系,求出AD的长;已知梯形的面积、上底和下底,根据梯形面积=(上底+下底)×高÷2,求出高AE的长度;用三角形DEC的底边CE乘以高AE除以2得到三角形的面积。
6.5.35;0.215;2500;3;5;3.09
解:535cm2=5.35dm2;21.5公顷=0.215平方千米;2.5t=2500kg;
3.05m2=3m25dm2;3元零9分=3.09元。
故答案为:5.35;0.215;2500;3;5;3.09。
1dm2=100cm2;1平方千米=100公顷;1t=1000kg;
1m2=100dm2;1元=100分;
低级单位的量化高级单位除以进率;高级单位的量化低级单位乘进率。
7.10;20
解:10× ×10÷2
=20÷2
=10(平方厘米)
10×2=20(平方厘米)。
故答案为:10;20。
这个三角形的面积=底×高÷2,其中,高=底×;与它等底等高平行四边形的面积=这个三角形的面积×2。
8.3
解:45×2÷(5+10)=90÷15=6(cm)
6÷2=3(cm)
故答案为:3。
已知梯形的上底、下底和面积,可以求出梯形的高;剪开后两纸片可以组成一个平行四边形,说明梯形ADEF和梯形EFBC的高相等,均为原梯形ABCD高的一半,同时也是所拼成的平行四边形长边所对应的高。
9.14;15
解:灯笼的面积:满格有7个,不满格有14个;
7+14÷2
=7+7
=14(个)
1×14=14(平方厘米)
小帆船的面积:
(8+4)×2÷2+2×3÷2
=12×2÷2+6÷2
=12+3
=15(平方厘米)。
故答案为:14;15。
计算不规则图形的面积,可以数格子,分别数出满格和不满格的数量,不满格的数量按半格计算,再加上满格的数量,就是灯笼的格子数,最后乘每个小方格的面积即可。
小帆船的面积=梯形的面积+三角形的面积,其中,梯形的面积=(上底+下底)×高÷2,三角形的面积=底×高÷2。
10.错误
解:平行四边形的高有无数条,直角三角形的高有三条。原题说法错误。
故答案为:错误。
三角形都有三条高;锐角三角形的三条高都在三角形的内部;直角三角形的两条高分别在两条直角边上,另一条高在三角形的内部;钝角三角形的钝角的两边上的高在三角形外部,另一条高在三角形的内部。
11.正确
解:用梯形的面积计算公式S梯=(上底+下底)×高÷2也可以计算三角形的面积,只要把梯形的上底看作0即可。说法正确。
故答案为:正确。
梯形的上底看作0,形状就变成了三角形,梯形的下底就是三角形的底边。
12.错误
解:若平行四边形与三角形等底等高,则平行四边形面积是三角形面积的2倍,原题说法错误。
故答案为:错误。
平行四边形面积=底×高,三角形面积=底×高÷2,据此判断。
13.错误
解:第一个、第二个和第四个图形是只有一组对边平行的四边形,所以是梯形;第三个图形是两组对边都不平行的四边形,不是梯形。
故答案为:错误。
根据只有一组对边平行的四边形叫做梯形进行判断即可。
14.正确
解:用两个完全一样的梯形可以拼成平行四边形,这个平行四边形的面积=梯形的面积×2;
平行四边形又可以切成两个完全一样的三角形,所以用梯形面积计算公式可以计算平行四边形和三角形的面积。
故答案为:正确。
用两个完全一样的梯形可以拼成平行四边形,用两个完全一样的三角形可以拼成平行四边形,据此计算。
15.B
解:三角形的面积是ad÷2或者ch÷2。
故答案为:B。
三角形的面积=底×高÷2,其中,底a上的高是d,底c上的高是h。
16.B
解:8÷2=4(平方厘米)。
故答案为:B。
三角形的面积=等底等高的平行四边形的面积÷2。
17.A
解:①的面积=②的面积=③的面积=④的面积。
故答案为:A。
三角形的面积=底×高÷2,等底等高的三角形面积相等。
18.C
解:如图,把一个平行四边形沿高剪拼成一个长方形,底和高都不变,则面积不变,但是平行四边形边的长度总和变小了,所以周长变小了。
故答案为:C。
根据题目给出条件作出图像,平行四边形的底边变成了长方形的长,没有变化,斜边变成了长方形的宽,比原来变短了,可知周长变短了;平行四边形面积=底×高,长方形面积=宽×长,可知面积没有变化。
19.C
解:6×4×2=48(平方厘米)
故答案为:C。
看图可知,三角形ABC的面积是拼成长方形面积的2倍,因此用长方形面积乘2即可求出三角形ABC的面积。
20.
由三条线段围成的封闭图形叫三角形;
平行四边形的对边平行且相等;
梯形只有一组对边平行;
三角形作高的方法:①把三角尺的一条直角边与已知底重合;②沿着底移动三角尺,使三角尺的另一条直角边通过这条底对面的顶点,沿这条直角边画一条直线,顶点与垂足之间的线段就是这个三角形的高;③在垂足处标出垂直符号;
平行四边形作高的方法:过平行四边形的一组对边上的一点向对边画垂线,这点与垂足之间的线段是平行四边形的高;
梯形作高的方法:过梯形的上底上的任意一点向下底画垂线,这点与垂足之间的线段是梯形的高,据此作图。
21.15
解:如图,连结AC
∵E在BC上,BE:EC = 1:2
∴S△ABE:S△ABC=BE:BC = 1:3
∴S△ABC
∵AC是平行四边形ABCD的对角线
∴S△ABC=S△ACD
∵F是CD的中点
∴S△AFD:S△ADC= DF:CD = 1:2
∴S△AFD=
答: 三角形ADF的面积是15cm2
故答案为:15
连接AC,则三角形ABC的面积等于三角形ADC的面积。 因为 BE∶EC=1∶2,则三角形ABE的面积:三角形ABC面积等于1:3
三角形ABC的面积 三角形ADF 的面积是三角形ADC的面积的一半,即
22.解:长方形面积=3×2=6;三角形底画6格,高画2格,三角形面积=6×2÷2=6;
平行四边形底画3格,高画2格,平行四边形面积=3×2=6;梯形的上底画2格,下底画4格,高画2格,梯形面积=(2+4)×2÷2=6;
长方形面积=长×宽,三角形面积=底×高÷2,平行四边形面积=底×高,梯形面积=(上底+下底)×高÷2。
23.解:根据题意,可得
答:准备3.9 kg肥料够。
根据三角形的面积公式:S=底×高÷2,求出蔬菜种植园的面积,然后再乘以每平方需要的化肥质量,然后再将克换算成千克,最后再跟3.9千克进行比较即可
24.解:7.2÷1.8=4(m)
答:这条高对应的底边长是4m。
平行四边形的面积=底×高,根据题意可得:平行四边形的面积÷高=这条高对应的底,据此解答即可。
25.解:[(30+20)+80]×50÷2
=[50+80]×50÷2
=130×50÷2
=6500÷2
=3250(平方米)
答:铺草皮的面积是3250平方米。
平移后铺草皮的面积合起来就是一个上底为(30+20)米,下底为80米,高为50米的梯形,梯形的面积=(上底+下底)×高÷2。
26.解:120×100=12000(平方米)
160×100-12000
=16000-12000
=4000(平方米)
4000×50=200000(元)
答:操场的占地面积是12000平方米;如果绿化带要铺上草坪,一共需要200000元。
观察图可知,操场的形状是平行四边形,要求操场的占地面积,应用公式:平行四边形的面积=底×高;绿化带的面积=大长方形的面积-操场的面积,然后用绿化带的面积×每平方米草坪的单价=铺草坪一共需要的总钱数。
27.解:连接 , 则.
而 (平方厘米)
所以 (平方厘米)
于是可得: E、F、o为BD的 4 等分点,
则 ( 平方厘米)
又因三角形 与三角形 是相似三角形, 且相似比为 , 则其面积比为 ,
所以 (平方厘米)
因此阴影部分的面积 (平方厘米)
答: 四边形EFGH的面积为7平方厘米。
关于平行四边形及其内部划分的面积计算问题。平行四边形ABCD的面积为36平方厘米,H和G分别是BC和CD边上的靠近B和D的三等分点,我们要找出四边形FEGH的面积。连接 后,找到各三角形与平行四边形面积之间的关系,通过比例和鸟头图形的性质进行计算。
同课章节目录
