2024-2025学年五年级数学上册寒假巩固练习(北师大版)第7练- 可能性(含答案+解析)
文档属性
| 名称 | 2024-2025学年五年级数学上册寒假巩固练习(北师大版)第7练- 可能性(含答案+解析) |  | |
| 格式 | docx | ||
| 文件大小 | 2.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-01-24 12:45:55 | ||
图片预览



文档简介
2024-2025学年五年级数学上册寒假巩固练习(北师大版)
第7练- 可能性
一、填一填(共23分)
1.经过某十字路口的汽车,它可能继续直行,也可能向左转或向右转,如果这三种可能性大小相同,那么两辆汽车经过这个十字路口,两辆车都走同一个方向的概率为 。
2.璎珞、长命锁和朝珠是常见的颈饰,妙妙班举办的“颈饰艺术之旅”活动会给同学们展示这三种颈饰,奇奇和妙妙是这场活动的讲解员。他们用抽纸条的方式决定谁先选择要讲解的颈饰,他们准备了15个写有璎珞、23个写有长命锁和11个写有朝珠的纸条,从中随机抽取一个,若抽中写有长命锁的纸条,奇奇先选,若抽中写有璎珞或朝珠的纸条,甜甜先选, 先选的可能性大。若要使规则公平,则需再放入 个写有 的纸条。
3. 一个不透明的袋子里放了一些除颜色外完全相同的小球,下面是奇奇的摸球情况记录(摸了40次,每次摸完后放回),袋子里 色的小球可能最多, 色的小球可能最少,要是再摸一次,摸到 色的小球的可能性最大。
红色球 蓝色球 绿色球
次数 22 5 13
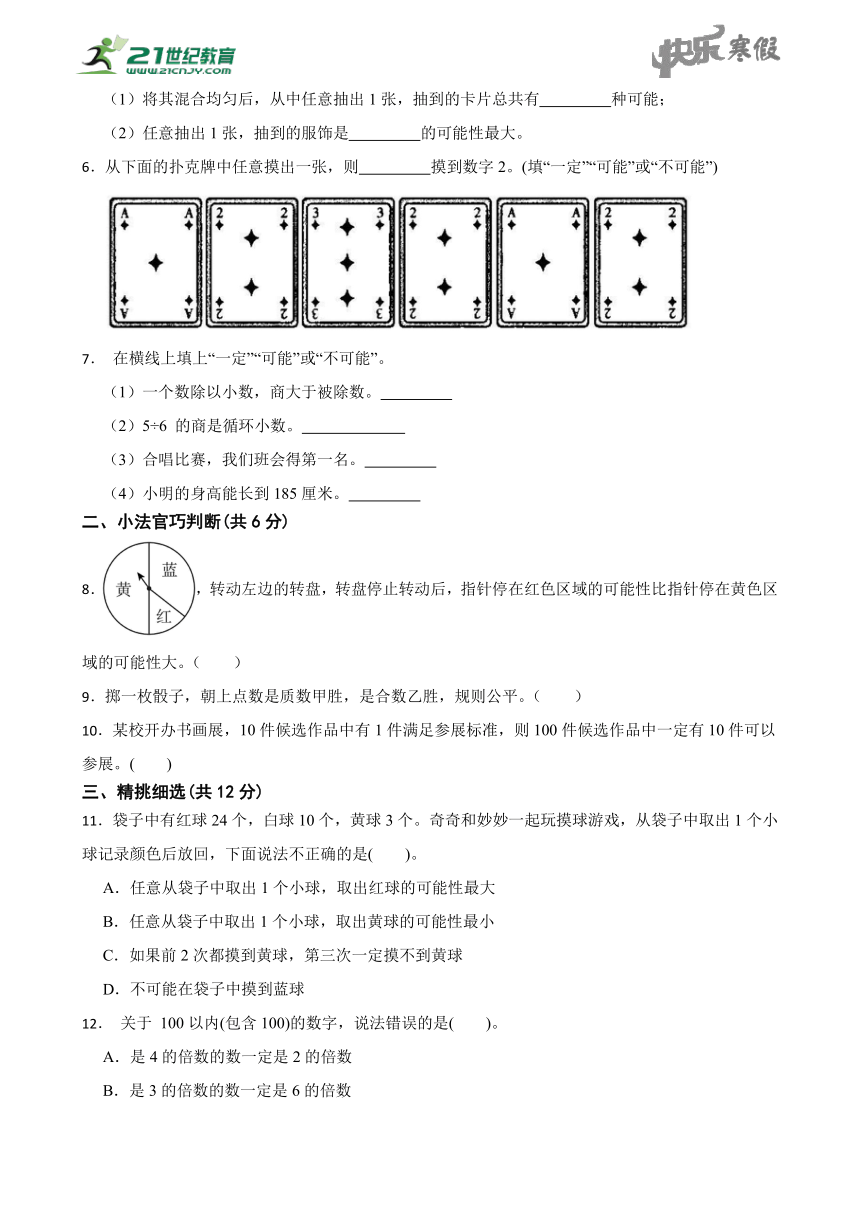
4.芳芳和军军准备从甲乙丙丁四个纸盒中选一个来玩摸球游戏,并制定了如下规则:两人轮流从盒中任意摸一个球,摸后放回,每人摸10次;如果摸出的是黑球,芳芳记1分;如果摸出的是白球,军军记1分;如果摸出的是灰球,都不记分。选( )盒玩游戏最公平。
A.甲 B.乙 C.丙 D.丁
5.妙妙依据古代服饰制作了如下的卡片。
(1)将其混合均匀后,从中任意抽出1张,抽到的卡片总共有 种可能;
(2)任意抽出1张,抽到的服饰是 的可能性最大。
6.从下面的扑克牌中任意摸出一张,则 摸到数字2。(填“一定”“可能”或“不可能”)
7. 在横线上填上“一定”“可能”或“不可能”。
(1)一个数除以小数,商大于被除数。
(2)5÷6 的商是循环小数。
(3)合唱比赛,我们班会得第一名。
(4)小明的身高能长到185厘米。
二、小法官巧判断(共6分)
8.,转动左边的转盘,转盘停止转动后,指针停在红色区域的可能性比指针停在黄色区域的可能性大。( )
9.掷一枚骰子,朝上点数是质数甲胜,是合数乙胜,规则公平。( )
10.某校开办书画展,10件候选作品中有1件满足参展标准,则100件候选作品中一定有10件可以参展。( )
三、精挑细选(共12分)
11.袋子中有红球24个,白球10个,黄球3个。奇奇和妙妙一起玩摸球游戏,从袋子中取出1个小球记录颜色后放回,下面说法不正确的是( )。
A.任意从袋子中取出1个小球,取出红球的可能性最大
B.任意从袋子中取出1个小球,取出黄球的可能性最小
C.如果前2次都摸到黄球,第三次一定摸不到黄球
D.不可能在袋子中摸到蓝球
12. 关于 100以内(包含100)的数字,说法错误的是( )。
A.是4的倍数的数一定是2的倍数
B.是3的倍数的数一定是6的倍数
C.是3的倍数的数比是4的倍数的数多
D.是2的倍数的数比是4的倍数的数多
13.在桌子上放了7张卡片,卡片除了数字外其他均相同。妙妙任意抽取一张卡片后放回并打乱,要求依据下表中抽取10次的结果判断这7张卡片上的数字最有可能是( )。
类型 一位数 两位数
次数 8 2
A.2,11,30,14,27,38,99 B.1,2,16,24,35,66,79
C.4,6,3,3,15,27,49 D.2,3,5,6,7,8,14
14. 奇奇在玩摸球游戏,表中是他摸出各种颜色球次数的记录(每次摸一个球,记录下颜色后放回盒子里)。
颜色 白球 黄球 红球
次数 8 4 5
下列说法正确的是( )。
A.盒子里装的红球一定最少
B.盒子里装的白球可能比红球多
C.盒子里白球的数量是黄球的2倍
15.某航模店为庆祝新一代载人飞船命名为“梦舟”,举办了线上抽券活动。下表是后台统计的80位顾客转转盘抽奖结果,根据表中数据,判断该店提供的抽奖转盘可能是( )。
5元优惠券 20元优惠券 谢谢参与
53人 13人 14人
A. B.
C. D.
16.奇奇和聪聪下五子棋,准备用摸球的方法来决定谁执白棋,所有球除颜色外其他完全相同,任意摸一个球,摸到红球奇奇执白棋,摸到蓝球聪聪执白棋,摸到黄球再摸一次。你认为从( )盒子里摸球是不公平的。
A. B.
C. D.
四、请你当个设计师(共18分)
17.涂一涂,使指针可能停在红色、蓝色的区域,并且停在红色区域的可能性较大。
18.给下图中的球涂上颜色,使它能满足下面的要求。
⑴不可能摸出红、黄、绿以外颜色的球。
⑵可能摸出红色的球。
⑶摸出绿色球的可能性最小。
⑷最容易摸到黄色的球。
五、数学小博士(共38分)
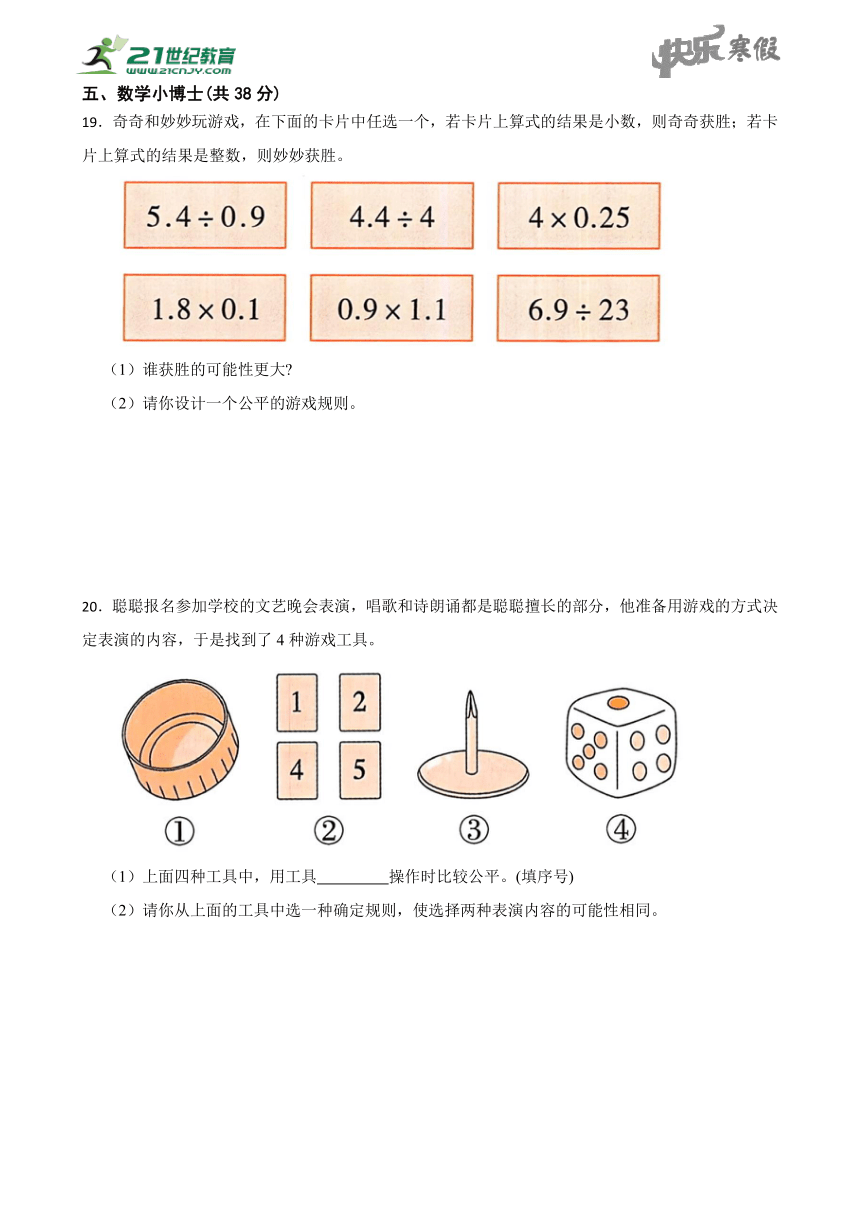
19.奇奇和妙妙玩游戏,在下面的卡片中任选一个,若卡片上算式的结果是小数,则奇奇获胜;若卡片上算式的结果是整数,则妙妙获胜。
(1)谁获胜的可能性更大
(2)请你设计一个公平的游戏规则。
20.聪聪报名参加学校的文艺晚会表演,唱歌和诗朗诵都是聪聪擅长的部分,他准备用游戏的方式决定表演的内容,于是找到了4种游戏工具。
(1)上面四种工具中,用工具 操作时比较公平。(填序号)
(2)请你从上面的工具中选一种确定规则,使选择两种表演内容的可能性相同。
21. 桌子上摆着19张卡片,分别写着2到20这几个数。任意摸一个数,若摸到双数,则聪聪赢;若摸到单数,则明明赢。
(1)这个游戏公平吗? 为什么?
(2)明明一定会输吗?
(3)怎样才能使游戏公平?
22.小巧和小亚做了8个大小相同的纸鹤,5个红色,3个白色。他们把8个纸鹤放入盒子里,两人轮流摸,每次摸出一个后立即放回。小巧摸到红色的就得1面红旗,小亚摸到白色的就得到1面红旗,谁的红旗多,谁就赢。
(1)小巧摸到红色的纸鹤和小亚摸到白色的纸鹤的可能性一样吗?
(2)这个游戏公平吗?为什么?
(3)如果每人摸5次,小巧一定会赢吗?
答案解析部分
1.
解:3÷9=。
故答案为:。
两辆车都走同一个方向有3种情况,两辆车共9种情况,则两辆车都走同一个方向的概率=3÷9=。
2.甜甜;3;长命锁
解:写有璎珞或朝珠纸条的数量是:15+11=26(个), 26>23, 所以抽中写有璎珞或朝珠的纸条的可能性更大,所以甜甜先选的可能性更大,若要规则公平,则需再放入26-23=3(个)写有长命锁的纸条。
故答案为:甜甜;3;长命锁。
此题主要考查了可能性的大小,根据条件,先求出写有璎珞或朝珠纸条的数量是多少,然后与写有长命锁的纸条数量对比,哪种数量多,先选的可能性就越大;若要游戏规则公平,将数量统一即可。
3.红;蓝;红
解:22>13>5,即红球>绿球>蓝球,再摸一次情况不变。
故答案为:红;蓝;红
分析摸球情况记录表:从表格中可以看到红球被摸到的次数为22次,绿球为13次,蓝球为5次。推测袋内红球的数量可能最多,因为摸到红球的次数最多;蓝球的数量可能最少,因为摸到蓝球的次数最少。预估摸球的可能性;根据前两步的分析,如果再摸一次,由于红球的数量可能最多,因此摸到红球的可能性最大。
4.D
解:只有丁项中黑球和白球的数量相同,则游戏规则是公平的。
故答案为:D。
本题主要考察的是游戏规则的公平性。公平的游戏规则应当保证每个参与者获胜(或获得某种优势)的概率是相等的。因此,我们需要对每个选项中的规则进行概率分析,以确定其是否满足公平性。
5.(1)4
(2)曲裾
解:(1)总共有4种服饰,分别是曲裾、袄裙、齐胸襦裙和对襟襦裙,所以任意抽1张,总共有4种可能。
(2)根据卡片可知,曲裾的卡片数量最多,所以任意抽取一张,抽到曲裾的可能性最大。
故答案为:4;曲裾
(1)根据卡片的服饰样式,可知,一共有曲裾、袄裙、齐胸襦裙和对襟襦裙四种,所以,一共有四种可能
(2)观察卡片可知,曲裾的数量最多,所以,任意取一张,抽到曲裾的可能性最大。
6.可能
解:根据题意,可得
扑克牌中数字“2”有3张,数字“3”有1张,数字“A”有2张,所以,有可能摸到数字“2”
故答案为:可能
观察六张扑克牌,可知,数字“2”的扑克牌有3张,“A”扑克牌有2张,数字“3”有1张,因为是任意摸出一张,所以,可能摸到的数字“2”
7.(1)可能。
(2):一定。
(3)可能。
(4)可能。
解:(1)一个数除以小数,商可能大于被除数;
(2)5÷6 的商是,即一定为循环小数;
(3) 合唱比赛,我们班可能会得第一名;
(4) 小明的身高可能能长到185厘米。
故答案为:可能;一定;可能;可能。
(1)一个不等于0的数除以小于1的数,则商大于被除数,一个不等于0的数除以大于1的数,则商小于被除数;(2)5÷6=为无线循环小数;(3)我们无法确定比赛的输赢;
(4)小明能长多高只能推测。
8.错误
解:指针停在红色区域的可能性比指针停在黄色区域的可能性小。
故答案为:错误。
转盘上哪种颜色的区域面积大,那么指针停在这种颜色区域的可能性就大。
9.错误
解:这个规则不公平。
故答案为:错误。
一枚骰子上的数是1~6,其中质数是:2、3、5,合数是4、6,质数比合数多,所以游戏不公平。
10.错误
解:根据题意,可得
某校开办书画展,10件候选作品中有1件满足参展标准,则100件候选作品中可能有10件可以参展。
故答案为:错误
10件候选作品中有1件满足参展标准,则100件候选作品中可能有10件参展。
11.C
解:根据题意,可得
红球的数量最多,所以,摸到红球的概率最大,故A正确
黄球的数量最少,所以,摸到黄球的概率最小,故B正确
因为从袋子中取出1个小球记录颜色后放回,所以,如果前2次都摸到黄球,第三次有可能会摸到黄球,故C错误
因为袋子里面没有蓝球,所以,不可能摸到蓝球,故D正确
故答案为:C
根据题干信息,可知,红球的数量最多,白球次之,黄球数量最少;因为从袋子中取出1个小球记录颜色后放回,所以,摸完球后黄球的数量不变,概率也不会变;因为袋子中没有篮球,所以,袋子中不可能摸到篮球,据此即可回答
12.B
解:4=2×2, 所以是4的倍数的数一定是2的倍数,A 正确;
27是3的倍数,但不是6的倍数,B 选项说法错误;
100以内2的倍数有50个,3的倍数有33个,4的倍数有25个,所以C、D选项说法正确。
故答案为:B。
一个数的因数是指可以整除这个数的数;一个数的倍数是指可以被这个数整除的数。
13.D
根据抽取10次的结果可知,抽到一位数的可能性远大于抽到两位数的可能性,所以在数量关系上,一位数的个数远大于两位数,即D项符合条件。
故答案为:D.
本题的关键在于理解随机抽取卡片后的结果与卡片上数字类型(一位数与两位数)的分布之间的关系。从题目给出的抽取结果来看,妙妙抽取10次卡片,其中8次抽到的是一位数,只有2次抽到了两位数。这暗示了在给定的卡片组中,一位数的卡片数量远大于两位数的卡片数量。因此,我们要找的卡片组合应该符合这一条件。
14.B
解:A:摸到红球的次数最少不能说明盒子里装的红球一定最少;
B:摸到白球的次数比红球多,子里装的白球可能比红球多;
C:摸到的白球的数量是黄球的2倍,盒子里白球的数量不一定是黄球的2倍。
故答案为:B。
摸到的球的颜色情况不能代表盒子里装的球的颜色情况。
15.C
解:A.5元优惠券有6个,20元优惠券和谢谢参与均为0,不符合,排除;
B.5元优惠券有4个,20元优惠券只有2个,谢谢参与为0个,抽中20元优惠券的结果应与谢谢参与数量相当,排除;
C.5元优惠券有4个,20元优惠券只有1个,谢谢参与为1个,抽中20元优惠券的结果与谢谢参与数量相当,符合;
D.5元优惠券有2个,20元优惠券有3个,谢谢参与有1个,抽中5元优惠券的数量比20元的优惠券和谢谢参与的数量少,不符合,排除
故答案为:C
观察表中的数据,5元优惠券最多,20元优惠券和谢谢参与抽中的结果差不多,所以转盘上5元优惠券的个数应该最多,20元优惠券和谢谢参与的个数应该接近或一样多,据此分析。
16.C
解:首先,明确公平游戏的基本条件:奇奇和聪聪摸到红球或蓝球的概率应该相等。这要求红球和蓝球的数量应当相等,这样才能保证在摸球时,无论奇奇还是聪聪都有相同的机会摸到决定执白棋的球色。
其次,考虑黄球的存在对公平性的影响。黄球虽然不直接决定谁执白棋,但其数量的增加意味着需要进行额外的摸球操作,这可能会间接影响红球和蓝球被摸到的频率。如果一个盒子中黄球数量过多,而红球和蓝球数量不相等,那么即使经过多次摸球,奇奇和聪聪摸到决定颜色球的概率仍然可能不相等。
最后,结合选项进行具体分析。假设A、B、C、D四个盒子中红球和蓝球的数量不完全相同,但黄球数量不同。为了确保游戏的公平性,红球和蓝球的数量应当相等,而黄球的数量对公平性没有直接影响,但过多的黄球可能会导致摸球次数增多,间接影响到公平性。因此,选择黄球数量多且红球和蓝球数量不相等的盒子作为不公平的选项。
故答案为:C
本题考查的是概率和公平性判断。公平性原则要求奇奇和聪聪摸到决定执白棋颜色的球(红球或蓝球)的概率相等。由于题目中提到摸到黄球需再摸一次,这意味着黄球不直接决定谁执白棋,而红球和蓝球则直接决定。因此,我们主要关注红球和蓝球的数量分布,以及黄球数量对公平性的影响。
17.解:
停在哪个区域的可能性大小与它在总面积中所占面积的大小有关,在总面积中占的面积大,停在这个区域的可能性就大。
18.
此题要求不可能摸出红、黄、绿以外颜色的球,则袋子里的球只有红、黄、绿三种颜色,要求哪种摸到的可能性最大,这种颜色的球最多,要求哪种摸到的可能性最小,这种颜色的球数量最少,据此涂色。
19.(1)解:5.4÷0.9=6,
4.4÷4=1.1,
4×0.25=1,
1.8×0.1=0.18,
0.9×1.1=0.99,
6.9÷23=0.3,
有2个算式的结果为整数,4个算式的结果为小数,所以奇奇获胜的可能性更大。
(2)解:若卡片上算式的结果大于等于1,则奇奇获胜;若卡片上算式的结果小于1,则妙妙获胜。
(1)分别计算每个算式的答案,比较结果是整数和是小数的数量,来判断谁获胜的可能性大;
要设计公平的游戏规则,需要让 奇奇和妙妙 获胜的可能性相等,由(1)可知,计算结果中有三个结果大于1,三个结果小于1,所以游戏规则可以是若卡片上算式的结果大于等于1,则奇奇获胜;若卡片上算式的结果小于1,则妙妙获胜,此时两个人获胜的可能性是一样的.
20.(1)②和④
(2)规则一:选择骰子,如果骰子的点数是1,3,5的话,选择唱歌;如果点数是2,4,6的话,选择诗朗诵。
规则二:选择卡片,如果抽到的卡片小于3,选择唱歌;如果抽到的卡片大于3,选择诗朗诵。
解:(1)图①工具两面不均匀,出现的结果可能性不相等,故不选;图②中四张卡片被抽到的可能性大小相等,可以选择该工具;图③也是不均匀,每个结果出现的可能性大小不一样,故不选;图④每个面出现的可能性大小相等,可以选择该工具。
故答案为:②和④
选择出现的每个事件可能性大小相等的工具;选择骰子,只要每个事件出现的可能性结果都是3种即可,选择卡片,只要每个事件出现的可能性结果都是2种即可。
21.(1)这个游戏不公平。因为在2到20这几个数中,单数有9个,双数有10个,所以聪聪赢的可能性比明明赢的可能性大,所以这个游戏不公平。
(2)明明不一定会输。
(3)去掉一张双数卡片或者增加一张单数卡片,游戏就公平了。
22.(1)解:小巧摸到红色的纸鹤和小亚摸到白色的纸鹤的可能性不一样。
(2)解:这个游戏不公平,因为小巧赢的可能性比小亚大。
(3)解:如果每人摸5次,小巧不一定会赢。
事件发生的可能性是有大小的,可能性的大小与它在总数中所占数量的多少有关,在总数中占的数量多,摸到的可能性就大,占的数量小,摸到的可能性就小,占的数量相等,摸到的可能性也相等;
判断一个游戏规则是否公平,可以先找出最简单事件发生的所有可能性,可能性相等,则公平,可能性不相等,则不公平。
第7练- 可能性
一、填一填(共23分)
1.经过某十字路口的汽车,它可能继续直行,也可能向左转或向右转,如果这三种可能性大小相同,那么两辆汽车经过这个十字路口,两辆车都走同一个方向的概率为 。
2.璎珞、长命锁和朝珠是常见的颈饰,妙妙班举办的“颈饰艺术之旅”活动会给同学们展示这三种颈饰,奇奇和妙妙是这场活动的讲解员。他们用抽纸条的方式决定谁先选择要讲解的颈饰,他们准备了15个写有璎珞、23个写有长命锁和11个写有朝珠的纸条,从中随机抽取一个,若抽中写有长命锁的纸条,奇奇先选,若抽中写有璎珞或朝珠的纸条,甜甜先选, 先选的可能性大。若要使规则公平,则需再放入 个写有 的纸条。
3. 一个不透明的袋子里放了一些除颜色外完全相同的小球,下面是奇奇的摸球情况记录(摸了40次,每次摸完后放回),袋子里 色的小球可能最多, 色的小球可能最少,要是再摸一次,摸到 色的小球的可能性最大。
红色球 蓝色球 绿色球
次数 22 5 13
4.芳芳和军军准备从甲乙丙丁四个纸盒中选一个来玩摸球游戏,并制定了如下规则:两人轮流从盒中任意摸一个球,摸后放回,每人摸10次;如果摸出的是黑球,芳芳记1分;如果摸出的是白球,军军记1分;如果摸出的是灰球,都不记分。选( )盒玩游戏最公平。
A.甲 B.乙 C.丙 D.丁
5.妙妙依据古代服饰制作了如下的卡片。
(1)将其混合均匀后,从中任意抽出1张,抽到的卡片总共有 种可能;
(2)任意抽出1张,抽到的服饰是 的可能性最大。
6.从下面的扑克牌中任意摸出一张,则 摸到数字2。(填“一定”“可能”或“不可能”)
7. 在横线上填上“一定”“可能”或“不可能”。
(1)一个数除以小数,商大于被除数。
(2)5÷6 的商是循环小数。
(3)合唱比赛,我们班会得第一名。
(4)小明的身高能长到185厘米。
二、小法官巧判断(共6分)
8.,转动左边的转盘,转盘停止转动后,指针停在红色区域的可能性比指针停在黄色区域的可能性大。( )
9.掷一枚骰子,朝上点数是质数甲胜,是合数乙胜,规则公平。( )
10.某校开办书画展,10件候选作品中有1件满足参展标准,则100件候选作品中一定有10件可以参展。( )
三、精挑细选(共12分)
11.袋子中有红球24个,白球10个,黄球3个。奇奇和妙妙一起玩摸球游戏,从袋子中取出1个小球记录颜色后放回,下面说法不正确的是( )。
A.任意从袋子中取出1个小球,取出红球的可能性最大
B.任意从袋子中取出1个小球,取出黄球的可能性最小
C.如果前2次都摸到黄球,第三次一定摸不到黄球
D.不可能在袋子中摸到蓝球
12. 关于 100以内(包含100)的数字,说法错误的是( )。
A.是4的倍数的数一定是2的倍数
B.是3的倍数的数一定是6的倍数
C.是3的倍数的数比是4的倍数的数多
D.是2的倍数的数比是4的倍数的数多
13.在桌子上放了7张卡片,卡片除了数字外其他均相同。妙妙任意抽取一张卡片后放回并打乱,要求依据下表中抽取10次的结果判断这7张卡片上的数字最有可能是( )。
类型 一位数 两位数
次数 8 2
A.2,11,30,14,27,38,99 B.1,2,16,24,35,66,79
C.4,6,3,3,15,27,49 D.2,3,5,6,7,8,14
14. 奇奇在玩摸球游戏,表中是他摸出各种颜色球次数的记录(每次摸一个球,记录下颜色后放回盒子里)。
颜色 白球 黄球 红球
次数 8 4 5
下列说法正确的是( )。
A.盒子里装的红球一定最少
B.盒子里装的白球可能比红球多
C.盒子里白球的数量是黄球的2倍
15.某航模店为庆祝新一代载人飞船命名为“梦舟”,举办了线上抽券活动。下表是后台统计的80位顾客转转盘抽奖结果,根据表中数据,判断该店提供的抽奖转盘可能是( )。
5元优惠券 20元优惠券 谢谢参与
53人 13人 14人
A. B.
C. D.
16.奇奇和聪聪下五子棋,准备用摸球的方法来决定谁执白棋,所有球除颜色外其他完全相同,任意摸一个球,摸到红球奇奇执白棋,摸到蓝球聪聪执白棋,摸到黄球再摸一次。你认为从( )盒子里摸球是不公平的。
A. B.
C. D.
四、请你当个设计师(共18分)
17.涂一涂,使指针可能停在红色、蓝色的区域,并且停在红色区域的可能性较大。
18.给下图中的球涂上颜色,使它能满足下面的要求。
⑴不可能摸出红、黄、绿以外颜色的球。
⑵可能摸出红色的球。
⑶摸出绿色球的可能性最小。
⑷最容易摸到黄色的球。
五、数学小博士(共38分)
19.奇奇和妙妙玩游戏,在下面的卡片中任选一个,若卡片上算式的结果是小数,则奇奇获胜;若卡片上算式的结果是整数,则妙妙获胜。
(1)谁获胜的可能性更大
(2)请你设计一个公平的游戏规则。
20.聪聪报名参加学校的文艺晚会表演,唱歌和诗朗诵都是聪聪擅长的部分,他准备用游戏的方式决定表演的内容,于是找到了4种游戏工具。
(1)上面四种工具中,用工具 操作时比较公平。(填序号)
(2)请你从上面的工具中选一种确定规则,使选择两种表演内容的可能性相同。
21. 桌子上摆着19张卡片,分别写着2到20这几个数。任意摸一个数,若摸到双数,则聪聪赢;若摸到单数,则明明赢。
(1)这个游戏公平吗? 为什么?
(2)明明一定会输吗?
(3)怎样才能使游戏公平?
22.小巧和小亚做了8个大小相同的纸鹤,5个红色,3个白色。他们把8个纸鹤放入盒子里,两人轮流摸,每次摸出一个后立即放回。小巧摸到红色的就得1面红旗,小亚摸到白色的就得到1面红旗,谁的红旗多,谁就赢。
(1)小巧摸到红色的纸鹤和小亚摸到白色的纸鹤的可能性一样吗?
(2)这个游戏公平吗?为什么?
(3)如果每人摸5次,小巧一定会赢吗?
答案解析部分
1.
解:3÷9=。
故答案为:。
两辆车都走同一个方向有3种情况,两辆车共9种情况,则两辆车都走同一个方向的概率=3÷9=。
2.甜甜;3;长命锁
解:写有璎珞或朝珠纸条的数量是:15+11=26(个), 26>23, 所以抽中写有璎珞或朝珠的纸条的可能性更大,所以甜甜先选的可能性更大,若要规则公平,则需再放入26-23=3(个)写有长命锁的纸条。
故答案为:甜甜;3;长命锁。
此题主要考查了可能性的大小,根据条件,先求出写有璎珞或朝珠纸条的数量是多少,然后与写有长命锁的纸条数量对比,哪种数量多,先选的可能性就越大;若要游戏规则公平,将数量统一即可。
3.红;蓝;红
解:22>13>5,即红球>绿球>蓝球,再摸一次情况不变。
故答案为:红;蓝;红
分析摸球情况记录表:从表格中可以看到红球被摸到的次数为22次,绿球为13次,蓝球为5次。推测袋内红球的数量可能最多,因为摸到红球的次数最多;蓝球的数量可能最少,因为摸到蓝球的次数最少。预估摸球的可能性;根据前两步的分析,如果再摸一次,由于红球的数量可能最多,因此摸到红球的可能性最大。
4.D
解:只有丁项中黑球和白球的数量相同,则游戏规则是公平的。
故答案为:D。
本题主要考察的是游戏规则的公平性。公平的游戏规则应当保证每个参与者获胜(或获得某种优势)的概率是相等的。因此,我们需要对每个选项中的规则进行概率分析,以确定其是否满足公平性。
5.(1)4
(2)曲裾
解:(1)总共有4种服饰,分别是曲裾、袄裙、齐胸襦裙和对襟襦裙,所以任意抽1张,总共有4种可能。
(2)根据卡片可知,曲裾的卡片数量最多,所以任意抽取一张,抽到曲裾的可能性最大。
故答案为:4;曲裾
(1)根据卡片的服饰样式,可知,一共有曲裾、袄裙、齐胸襦裙和对襟襦裙四种,所以,一共有四种可能
(2)观察卡片可知,曲裾的数量最多,所以,任意取一张,抽到曲裾的可能性最大。
6.可能
解:根据题意,可得
扑克牌中数字“2”有3张,数字“3”有1张,数字“A”有2张,所以,有可能摸到数字“2”
故答案为:可能
观察六张扑克牌,可知,数字“2”的扑克牌有3张,“A”扑克牌有2张,数字“3”有1张,因为是任意摸出一张,所以,可能摸到的数字“2”
7.(1)可能。
(2):一定。
(3)可能。
(4)可能。
解:(1)一个数除以小数,商可能大于被除数;
(2)5÷6 的商是,即一定为循环小数;
(3) 合唱比赛,我们班可能会得第一名;
(4) 小明的身高可能能长到185厘米。
故答案为:可能;一定;可能;可能。
(1)一个不等于0的数除以小于1的数,则商大于被除数,一个不等于0的数除以大于1的数,则商小于被除数;(2)5÷6=为无线循环小数;(3)我们无法确定比赛的输赢;
(4)小明能长多高只能推测。
8.错误
解:指针停在红色区域的可能性比指针停在黄色区域的可能性小。
故答案为:错误。
转盘上哪种颜色的区域面积大,那么指针停在这种颜色区域的可能性就大。
9.错误
解:这个规则不公平。
故答案为:错误。
一枚骰子上的数是1~6,其中质数是:2、3、5,合数是4、6,质数比合数多,所以游戏不公平。
10.错误
解:根据题意,可得
某校开办书画展,10件候选作品中有1件满足参展标准,则100件候选作品中可能有10件可以参展。
故答案为:错误
10件候选作品中有1件满足参展标准,则100件候选作品中可能有10件参展。
11.C
解:根据题意,可得
红球的数量最多,所以,摸到红球的概率最大,故A正确
黄球的数量最少,所以,摸到黄球的概率最小,故B正确
因为从袋子中取出1个小球记录颜色后放回,所以,如果前2次都摸到黄球,第三次有可能会摸到黄球,故C错误
因为袋子里面没有蓝球,所以,不可能摸到蓝球,故D正确
故答案为:C
根据题干信息,可知,红球的数量最多,白球次之,黄球数量最少;因为从袋子中取出1个小球记录颜色后放回,所以,摸完球后黄球的数量不变,概率也不会变;因为袋子中没有篮球,所以,袋子中不可能摸到篮球,据此即可回答
12.B
解:4=2×2, 所以是4的倍数的数一定是2的倍数,A 正确;
27是3的倍数,但不是6的倍数,B 选项说法错误;
100以内2的倍数有50个,3的倍数有33个,4的倍数有25个,所以C、D选项说法正确。
故答案为:B。
一个数的因数是指可以整除这个数的数;一个数的倍数是指可以被这个数整除的数。
13.D
根据抽取10次的结果可知,抽到一位数的可能性远大于抽到两位数的可能性,所以在数量关系上,一位数的个数远大于两位数,即D项符合条件。
故答案为:D.
本题的关键在于理解随机抽取卡片后的结果与卡片上数字类型(一位数与两位数)的分布之间的关系。从题目给出的抽取结果来看,妙妙抽取10次卡片,其中8次抽到的是一位数,只有2次抽到了两位数。这暗示了在给定的卡片组中,一位数的卡片数量远大于两位数的卡片数量。因此,我们要找的卡片组合应该符合这一条件。
14.B
解:A:摸到红球的次数最少不能说明盒子里装的红球一定最少;
B:摸到白球的次数比红球多,子里装的白球可能比红球多;
C:摸到的白球的数量是黄球的2倍,盒子里白球的数量不一定是黄球的2倍。
故答案为:B。
摸到的球的颜色情况不能代表盒子里装的球的颜色情况。
15.C
解:A.5元优惠券有6个,20元优惠券和谢谢参与均为0,不符合,排除;
B.5元优惠券有4个,20元优惠券只有2个,谢谢参与为0个,抽中20元优惠券的结果应与谢谢参与数量相当,排除;
C.5元优惠券有4个,20元优惠券只有1个,谢谢参与为1个,抽中20元优惠券的结果与谢谢参与数量相当,符合;
D.5元优惠券有2个,20元优惠券有3个,谢谢参与有1个,抽中5元优惠券的数量比20元的优惠券和谢谢参与的数量少,不符合,排除
故答案为:C
观察表中的数据,5元优惠券最多,20元优惠券和谢谢参与抽中的结果差不多,所以转盘上5元优惠券的个数应该最多,20元优惠券和谢谢参与的个数应该接近或一样多,据此分析。
16.C
解:首先,明确公平游戏的基本条件:奇奇和聪聪摸到红球或蓝球的概率应该相等。这要求红球和蓝球的数量应当相等,这样才能保证在摸球时,无论奇奇还是聪聪都有相同的机会摸到决定执白棋的球色。
其次,考虑黄球的存在对公平性的影响。黄球虽然不直接决定谁执白棋,但其数量的增加意味着需要进行额外的摸球操作,这可能会间接影响红球和蓝球被摸到的频率。如果一个盒子中黄球数量过多,而红球和蓝球数量不相等,那么即使经过多次摸球,奇奇和聪聪摸到决定颜色球的概率仍然可能不相等。
最后,结合选项进行具体分析。假设A、B、C、D四个盒子中红球和蓝球的数量不完全相同,但黄球数量不同。为了确保游戏的公平性,红球和蓝球的数量应当相等,而黄球的数量对公平性没有直接影响,但过多的黄球可能会导致摸球次数增多,间接影响到公平性。因此,选择黄球数量多且红球和蓝球数量不相等的盒子作为不公平的选项。
故答案为:C
本题考查的是概率和公平性判断。公平性原则要求奇奇和聪聪摸到决定执白棋颜色的球(红球或蓝球)的概率相等。由于题目中提到摸到黄球需再摸一次,这意味着黄球不直接决定谁执白棋,而红球和蓝球则直接决定。因此,我们主要关注红球和蓝球的数量分布,以及黄球数量对公平性的影响。
17.解:
停在哪个区域的可能性大小与它在总面积中所占面积的大小有关,在总面积中占的面积大,停在这个区域的可能性就大。
18.
此题要求不可能摸出红、黄、绿以外颜色的球,则袋子里的球只有红、黄、绿三种颜色,要求哪种摸到的可能性最大,这种颜色的球最多,要求哪种摸到的可能性最小,这种颜色的球数量最少,据此涂色。
19.(1)解:5.4÷0.9=6,
4.4÷4=1.1,
4×0.25=1,
1.8×0.1=0.18,
0.9×1.1=0.99,
6.9÷23=0.3,
有2个算式的结果为整数,4个算式的结果为小数,所以奇奇获胜的可能性更大。
(2)解:若卡片上算式的结果大于等于1,则奇奇获胜;若卡片上算式的结果小于1,则妙妙获胜。
(1)分别计算每个算式的答案,比较结果是整数和是小数的数量,来判断谁获胜的可能性大;
要设计公平的游戏规则,需要让 奇奇和妙妙 获胜的可能性相等,由(1)可知,计算结果中有三个结果大于1,三个结果小于1,所以游戏规则可以是若卡片上算式的结果大于等于1,则奇奇获胜;若卡片上算式的结果小于1,则妙妙获胜,此时两个人获胜的可能性是一样的.
20.(1)②和④
(2)规则一:选择骰子,如果骰子的点数是1,3,5的话,选择唱歌;如果点数是2,4,6的话,选择诗朗诵。
规则二:选择卡片,如果抽到的卡片小于3,选择唱歌;如果抽到的卡片大于3,选择诗朗诵。
解:(1)图①工具两面不均匀,出现的结果可能性不相等,故不选;图②中四张卡片被抽到的可能性大小相等,可以选择该工具;图③也是不均匀,每个结果出现的可能性大小不一样,故不选;图④每个面出现的可能性大小相等,可以选择该工具。
故答案为:②和④
选择出现的每个事件可能性大小相等的工具;选择骰子,只要每个事件出现的可能性结果都是3种即可,选择卡片,只要每个事件出现的可能性结果都是2种即可。
21.(1)这个游戏不公平。因为在2到20这几个数中,单数有9个,双数有10个,所以聪聪赢的可能性比明明赢的可能性大,所以这个游戏不公平。
(2)明明不一定会输。
(3)去掉一张双数卡片或者增加一张单数卡片,游戏就公平了。
22.(1)解:小巧摸到红色的纸鹤和小亚摸到白色的纸鹤的可能性不一样。
(2)解:这个游戏不公平,因为小巧赢的可能性比小亚大。
(3)解:如果每人摸5次,小巧不一定会赢。
事件发生的可能性是有大小的,可能性的大小与它在总数中所占数量的多少有关,在总数中占的数量多,摸到的可能性就大,占的数量小,摸到的可能性就小,占的数量相等,摸到的可能性也相等;
判断一个游戏规则是否公平,可以先找出最简单事件发生的所有可能性,可能性相等,则公平,可能性不相等,则不公平。
同课章节目录
