2025高考数学考二轮专题型专项练6解答题组合练(c)-专项训练(含解析)
文档属性
| 名称 | 2025高考数学考二轮专题型专项练6解答题组合练(c)-专项训练(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 108.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-01-24 18:40:02 | ||
图片预览



文档简介
2025高考数学考二轮专题型专项练6 解答题组合练(c)-专项训练
1.已知α∈(0,π),sin α+cos α=,且cos α>sin α.
(1)求角α的大小;
(2)若x∈,给出m的一个合适的数值,使得函数y=sin x+2sin2(+α)的值域为(-+1].
2.(2024·广西桂林三模)已知数列{an}的前n项和为Sn,且4a1-3Sn=.
(1)求数列{an}的通项公式;
(2)设bn=nan,且数列{bn}的前n项和为Tn,若 n∈N*都有不等式Tn≤+3λan恒成立,求λ的取值范围.
3.某学校组织了环保知识竞赛活动,并从中抽取了200份试卷进行调查,这200份试卷的成绩(卷面共100分)频率分布直方图如图所示.
(1)用样本估计总体,求此次知识竞赛的平均分(同一组中的数据用该组区间的中点值为代表).
(2)可以认为这次竞赛成绩X近似地服从正态分布N(μ,σ2)(用样本平均数和标准差s分别作为μ,σ的近似值).已知样本标准差s≈7.36,若有84.14%的学生的竞赛成绩不低于学校期望的平均分,则学校期望的平均分约为多少(结果取整数)
(3)从[80,100]的试卷中用比例分配的分层随机抽样的方法抽取10份试卷,再从这10份样本中随机抽测i(1≤i≤6)份试卷(抽测的份数是随机的),若已知抽测的i份试卷都不低于90分,求抽测3份的概率.
参考数据:若X~N(μ,σ2),则P(μ-σ≤X≤μ+σ)≈0.682 7,P(μ-2σ≤X≤μ+2σ)≈0.954 5,P(μ-3σ≤X≤μ+3σ)≈0.997 3.
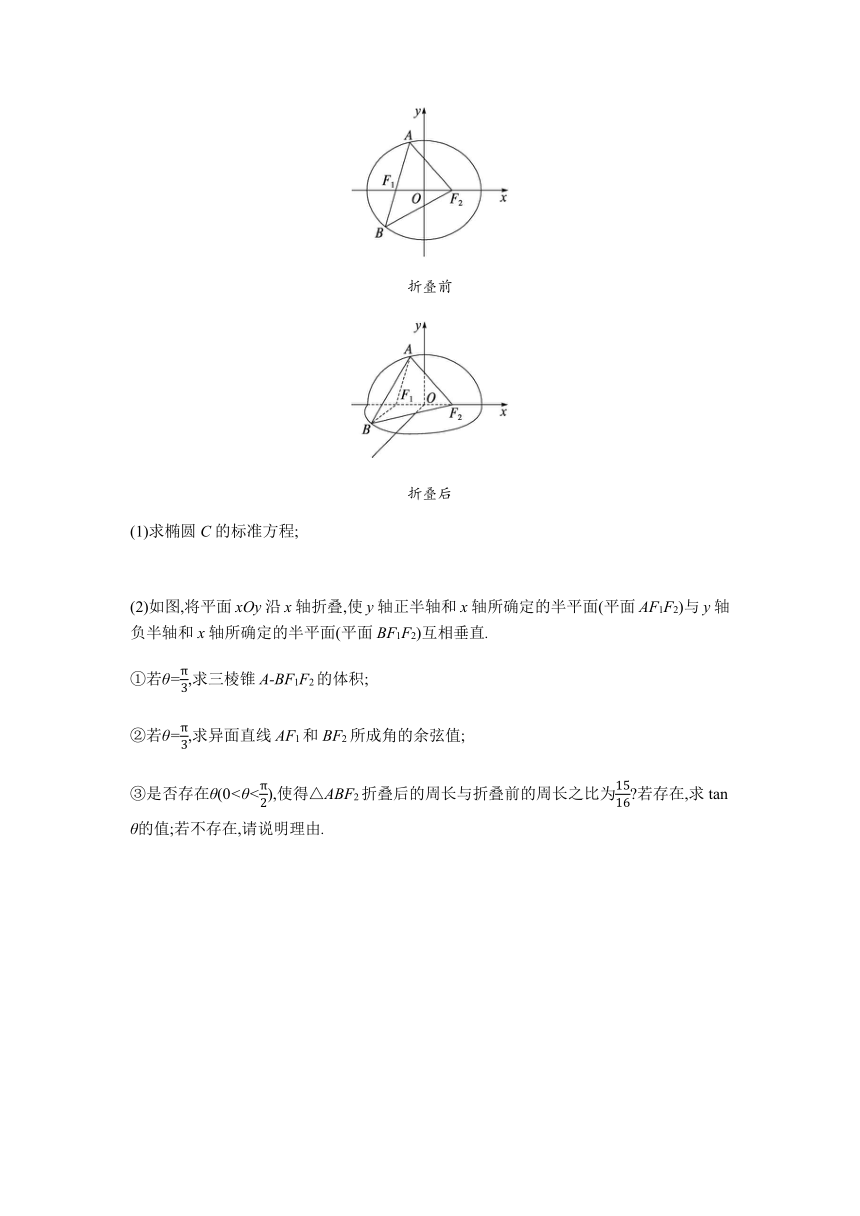
4.已知椭圆C:=1(a>0,b>0)的左、右焦点分别为F1,F2,离心率为,经过点F1且倾斜角为θ(0<θ<)的直线l与椭圆交于A,B两点(其中点A在x轴上方),△ABF2的周长为8.
折叠前
折叠后
(1)求椭圆C的标准方程;
(2)如图,将平面xOy沿x轴折叠,使y轴正半轴和x轴所确定的半平面(平面AF1F2)与y轴负半轴和x轴所确定的半平面(平面BF1F2)互相垂直.
①若θ=,求三棱锥A-BF1F2的体积;
②若θ=,求异面直线AF1和BF2所成角的余弦值;
③是否存在θ(0<θ<),使得△ABF2折叠后的周长与折叠前的周长之比为 若存在,求tan θ的值;若不存在,请说明理由.
5.(2024·九省联考)离散对数在密码学中有重要的应用.设p是素数,集合X={1,2,…,p-1},若u,v∈X,m∈N,记u v为uv除以p的余数,um, 为um除以p的余数;设a∈X,1,a,a2, ,…,ap-2, 两两不同,若an, =b(n∈{0,1,…,p-2}),则称n是以a为底b的离散对数,记为n=log(p)ab.
(1)若p=11,a=2,求ap-1, ;
(2)对m1,m2∈{0,1,…,p-2},记m1 m2为m1+m2除以p-1的余数(当m1+m2能被p-1整除时,m1 m2=0),证明:log(p)a(b c)=log(p)ab log(p)ac,其中b,c∈X;
(3)已知n=log(p)ab.对x∈X,k∈{1,2,…,p-2},令y1=ak, ,y2=x bk, ,证明:x=y2.
题型专项练6 解答题组合练(C) 答案
1.解 (1)因为sin α+cos α=sin,
所以sin(α+)=.
又α∈(0,π),所以α+,
可得α+,可得α=.
又cos α>sin α,所以α=.
(2)y=sin x+2sin2=sin x+1-cos=sin x+1-cos xcos+sin xsinsin x-cos x+1
=sin+1.
当x=-时,y=sin+1=-,当sin=1时,y=+1,
所以由题意可得m-,可得m>.
因此m∈即可,故m的值可取π.
2.解 (1)因为4a1-3Sn=,
当n=1时可得4a1-3a1=1,即a1=1≠0,3Sn=4-①,
当n≥2时,3Sn-1=4-②,
由①-②得3an=,an=,又a1=1也满足,所以an=()n-1.
(2)因为bn=nan=n()n-1,所以Tn=1×()0+2×()1+3×()2+…+n×()n-1③,
Tn=1×()1+2×()2+…+(n-1)×()n-1+n×()n④,
③-④得,Tn=()0+()1+()2+…+()n-1-n×()n,
即Tn=-n×()n,则Tn=-(n+)()n,
故Tn=(n+)()n.
由Tn≤+3λan,得(n+)()n≤+3λ()n-1,即λ≥-,
依题意, n∈N*不等式λ≥-恒成立,
因为y=-随着n增大而减小,所以λ≥-,
即λ的取值范围为[-,+∞).
3.解 (1)由频率分布直方图可知,
平均分为(65×0.01+75×0.04+85×0.035+95×0.015)×10=80.5.
(2)由(1)可知X~N(80.5,7.362),设学校期望的平均分约为m,则P(X≥m)=0.841 4.
因为P(μ-σ≤X≤μ+σ)≈0.682 7,P(μ-σ≤X≤μ)≈0.341 4,
所以P(X≥μ-σ)≈0.841 4,
即P(X≥73.14)≈0.841 4,
所以学校期望的平均分约为73分.
(3)由频率分布直方图可知,分数在[80,90)和[90,100]的频率分别为0.35和0.15,那么按照比例分配的分层随机抽样抽取10人,其中分数在[80,90)的应抽取10×=7人,
分数在[90,100]的应抽取10×=3人.
记事件Ai:抽测i(i=1,2,3)份试卷,事件B:取出的试卷都不低于90分,
则P(Ai)=,P(B|Ai)=,
P(B)=P(Ai)P(B|Ai)=×()=,
则P(A3|B)=.
4.解 (1)由椭圆的定义知,|AF1|+|AF2|=2a,|BF1|+|BF2|=2a,
所以△ABF2的周长L=4a=8,所以a=2.
又椭圆离心率为,所以,所以c=1,b2=a2-c2=3,
由题意,椭圆的焦点在x轴上,所以椭圆的标准方程为=1.
(2)①因为直线l过F1(-1,0),所以直线l:y-0=(x+1),y-0=(x+1)与=1联立得解得
所以A(0,)(因为点A在x轴上方)以及B(-,-),|AF1|=2,|BF1|=,V=|BF1||F1F2|sin 120°|AF1|sin 60°=.
②以O为坐标原点,折叠后原y轴负半轴、原x轴、原y轴正半轴所在直线为x轴、y轴、z轴建立空间直角坐标系,则F1(0,-1,0),A(0,0,),B(,-,0),F2(0,1,0),
=(0,1,),=-,0.
记异面直线AF1和BF2所成角为φ,则cos φ=|cos<>|=.
③存在,理由如下:设折叠前A(x1,y1),B(x2,y2),折叠后A,B在新图形中对应点记为A',B',A'(x1,y1,0),B'(x2,0,-y2),折叠前△ABF2周长是8,则折叠后△A'B'F2周长是,
由|A'F2|+|B'F2|+|A'B'|=,|AF2|+|BF2|+|AB|=8,
故|AB|-|A'B'|=,
设l方程为my=x+1,
由得(3m2+4)y2-6my-9=0,
则y1+y2=,y1y2=,
如图,在折叠后的图形中建立空间直角坐标系(原x轴仍然为x轴,原y轴正半轴为y轴,原y轴负半轴为z轴),
|A'B'|=,|AB|=,
所以|AB|-|A'B'|=(ⅰ),
又,所以=-4y1y2(ⅱ),
由(ⅰ)+(ⅱ)可得-2y1y2,
因为(x1-x2)2+(y1-y2)2=(1+m2)(y1-y2)2=(-2y1y2)2,
所以(1+m2)[()2+]=()2,
即144()2=()2,
所以,解得m2=,
因为0<θ<,所以tan θ=.
5.(1)解 若p=11,a=2,又注意到210=1 024=93×11+1,所以ap-1, =210, =1.
(2)证明 当p=2时,此时X={1},此时b=c=1,b c=1,
故log(p)a(b c)=0,log(p)ab=0,log(p)ac=0,
此时log(p)a(b c)=log(p)ab log(p)ac.
当p>2时,因为1,a,a2, ,…,ap-2, 两两不同,故a≥2,
又a∈X,故a,p互质,
设n=log(p)a(b c),n1=log(p)ab,n2=log(p)ac,
则 m1,m2∈N,使得=pm1+b,=pm2+c,
所以=(pm1+b)(pm2+c),故≡bc(mod p).
设n1+n2=t(p-1)+s,0≤s≤p-2,则n1 n2=s,
因为1,2,3,…,p-1除以p的余数两两不同,
且a,2a,3a,…,(p-1)a除以p的余数两两不同,
所以(p-1)!≡[a×2a×3a×…×(p-1)a](mod p),所以ap-1≡1mod p,
所以as≡bc(mod p),又an≡b c(mod p)=bc(mod p),其中0≤n≤p-2,
所以s=n,即log(p)a(b c)=log(p)ab log(p)ac.
(3)证明 当b≥2时,由(2)可得bp-1≡1mod p,若b=1,则bp-1≡1mod p也成立.
因为n=log(p)ab,所以an≡b(mod p).
y2 ≡y2≡(x bk, )·(ak, )n(p-2)≡(xbk)akn(p-2)≡(xbk)bk(p-2)≡x(bp-1)k-1≡x(1)k-1(mod p)≡x(mod p).
因为x∈X,所以x=y2
1.已知α∈(0,π),sin α+cos α=,且cos α>sin α.
(1)求角α的大小;
(2)若x∈,给出m的一个合适的数值,使得函数y=sin x+2sin2(+α)的值域为(-+1].
2.(2024·广西桂林三模)已知数列{an}的前n项和为Sn,且4a1-3Sn=.
(1)求数列{an}的通项公式;
(2)设bn=nan,且数列{bn}的前n项和为Tn,若 n∈N*都有不等式Tn≤+3λan恒成立,求λ的取值范围.
3.某学校组织了环保知识竞赛活动,并从中抽取了200份试卷进行调查,这200份试卷的成绩(卷面共100分)频率分布直方图如图所示.
(1)用样本估计总体,求此次知识竞赛的平均分(同一组中的数据用该组区间的中点值为代表).
(2)可以认为这次竞赛成绩X近似地服从正态分布N(μ,σ2)(用样本平均数和标准差s分别作为μ,σ的近似值).已知样本标准差s≈7.36,若有84.14%的学生的竞赛成绩不低于学校期望的平均分,则学校期望的平均分约为多少(结果取整数)
(3)从[80,100]的试卷中用比例分配的分层随机抽样的方法抽取10份试卷,再从这10份样本中随机抽测i(1≤i≤6)份试卷(抽测的份数是随机的),若已知抽测的i份试卷都不低于90分,求抽测3份的概率.
参考数据:若X~N(μ,σ2),则P(μ-σ≤X≤μ+σ)≈0.682 7,P(μ-2σ≤X≤μ+2σ)≈0.954 5,P(μ-3σ≤X≤μ+3σ)≈0.997 3.
4.已知椭圆C:=1(a>0,b>0)的左、右焦点分别为F1,F2,离心率为,经过点F1且倾斜角为θ(0<θ<)的直线l与椭圆交于A,B两点(其中点A在x轴上方),△ABF2的周长为8.
折叠前
折叠后
(1)求椭圆C的标准方程;
(2)如图,将平面xOy沿x轴折叠,使y轴正半轴和x轴所确定的半平面(平面AF1F2)与y轴负半轴和x轴所确定的半平面(平面BF1F2)互相垂直.
①若θ=,求三棱锥A-BF1F2的体积;
②若θ=,求异面直线AF1和BF2所成角的余弦值;
③是否存在θ(0<θ<),使得△ABF2折叠后的周长与折叠前的周长之比为 若存在,求tan θ的值;若不存在,请说明理由.
5.(2024·九省联考)离散对数在密码学中有重要的应用.设p是素数,集合X={1,2,…,p-1},若u,v∈X,m∈N,记u v为uv除以p的余数,um, 为um除以p的余数;设a∈X,1,a,a2, ,…,ap-2, 两两不同,若an, =b(n∈{0,1,…,p-2}),则称n是以a为底b的离散对数,记为n=log(p)ab.
(1)若p=11,a=2,求ap-1, ;
(2)对m1,m2∈{0,1,…,p-2},记m1 m2为m1+m2除以p-1的余数(当m1+m2能被p-1整除时,m1 m2=0),证明:log(p)a(b c)=log(p)ab log(p)ac,其中b,c∈X;
(3)已知n=log(p)ab.对x∈X,k∈{1,2,…,p-2},令y1=ak, ,y2=x bk, ,证明:x=y2.
题型专项练6 解答题组合练(C) 答案
1.解 (1)因为sin α+cos α=sin,
所以sin(α+)=.
又α∈(0,π),所以α+,
可得α+,可得α=.
又cos α>sin α,所以α=.
(2)y=sin x+2sin2=sin x+1-cos=sin x+1-cos xcos+sin xsinsin x-cos x+1
=sin+1.
当x=-时,y=sin+1=-,当sin=1时,y=+1,
所以由题意可得m-,可得m>.
因此m∈即可,故m的值可取π.
2.解 (1)因为4a1-3Sn=,
当n=1时可得4a1-3a1=1,即a1=1≠0,3Sn=4-①,
当n≥2时,3Sn-1=4-②,
由①-②得3an=,an=,又a1=1也满足,所以an=()n-1.
(2)因为bn=nan=n()n-1,所以Tn=1×()0+2×()1+3×()2+…+n×()n-1③,
Tn=1×()1+2×()2+…+(n-1)×()n-1+n×()n④,
③-④得,Tn=()0+()1+()2+…+()n-1-n×()n,
即Tn=-n×()n,则Tn=-(n+)()n,
故Tn=(n+)()n.
由Tn≤+3λan,得(n+)()n≤+3λ()n-1,即λ≥-,
依题意, n∈N*不等式λ≥-恒成立,
因为y=-随着n增大而减小,所以λ≥-,
即λ的取值范围为[-,+∞).
3.解 (1)由频率分布直方图可知,
平均分为(65×0.01+75×0.04+85×0.035+95×0.015)×10=80.5.
(2)由(1)可知X~N(80.5,7.362),设学校期望的平均分约为m,则P(X≥m)=0.841 4.
因为P(μ-σ≤X≤μ+σ)≈0.682 7,P(μ-σ≤X≤μ)≈0.341 4,
所以P(X≥μ-σ)≈0.841 4,
即P(X≥73.14)≈0.841 4,
所以学校期望的平均分约为73分.
(3)由频率分布直方图可知,分数在[80,90)和[90,100]的频率分别为0.35和0.15,那么按照比例分配的分层随机抽样抽取10人,其中分数在[80,90)的应抽取10×=7人,
分数在[90,100]的应抽取10×=3人.
记事件Ai:抽测i(i=1,2,3)份试卷,事件B:取出的试卷都不低于90分,
则P(Ai)=,P(B|Ai)=,
P(B)=P(Ai)P(B|Ai)=×()=,
则P(A3|B)=.
4.解 (1)由椭圆的定义知,|AF1|+|AF2|=2a,|BF1|+|BF2|=2a,
所以△ABF2的周长L=4a=8,所以a=2.
又椭圆离心率为,所以,所以c=1,b2=a2-c2=3,
由题意,椭圆的焦点在x轴上,所以椭圆的标准方程为=1.
(2)①因为直线l过F1(-1,0),所以直线l:y-0=(x+1),y-0=(x+1)与=1联立得解得
所以A(0,)(因为点A在x轴上方)以及B(-,-),|AF1|=2,|BF1|=,V=|BF1||F1F2|sin 120°|AF1|sin 60°=.
②以O为坐标原点,折叠后原y轴负半轴、原x轴、原y轴正半轴所在直线为x轴、y轴、z轴建立空间直角坐标系,则F1(0,-1,0),A(0,0,),B(,-,0),F2(0,1,0),
=(0,1,),=-,0.
记异面直线AF1和BF2所成角为φ,则cos φ=|cos<>|=.
③存在,理由如下:设折叠前A(x1,y1),B(x2,y2),折叠后A,B在新图形中对应点记为A',B',A'(x1,y1,0),B'(x2,0,-y2),折叠前△ABF2周长是8,则折叠后△A'B'F2周长是,
由|A'F2|+|B'F2|+|A'B'|=,|AF2|+|BF2|+|AB|=8,
故|AB|-|A'B'|=,
设l方程为my=x+1,
由得(3m2+4)y2-6my-9=0,
则y1+y2=,y1y2=,
如图,在折叠后的图形中建立空间直角坐标系(原x轴仍然为x轴,原y轴正半轴为y轴,原y轴负半轴为z轴),
|A'B'|=,|AB|=,
所以|AB|-|A'B'|=(ⅰ),
又,所以=-4y1y2(ⅱ),
由(ⅰ)+(ⅱ)可得-2y1y2,
因为(x1-x2)2+(y1-y2)2=(1+m2)(y1-y2)2=(-2y1y2)2,
所以(1+m2)[()2+]=()2,
即144()2=()2,
所以,解得m2=,
因为0<θ<,所以tan θ=.
5.(1)解 若p=11,a=2,又注意到210=1 024=93×11+1,所以ap-1, =210, =1.
(2)证明 当p=2时,此时X={1},此时b=c=1,b c=1,
故log(p)a(b c)=0,log(p)ab=0,log(p)ac=0,
此时log(p)a(b c)=log(p)ab log(p)ac.
当p>2时,因为1,a,a2, ,…,ap-2, 两两不同,故a≥2,
又a∈X,故a,p互质,
设n=log(p)a(b c),n1=log(p)ab,n2=log(p)ac,
则 m1,m2∈N,使得=pm1+b,=pm2+c,
所以=(pm1+b)(pm2+c),故≡bc(mod p).
设n1+n2=t(p-1)+s,0≤s≤p-2,则n1 n2=s,
因为1,2,3,…,p-1除以p的余数两两不同,
且a,2a,3a,…,(p-1)a除以p的余数两两不同,
所以(p-1)!≡[a×2a×3a×…×(p-1)a](mod p),所以ap-1≡1mod p,
所以as≡bc(mod p),又an≡b c(mod p)=bc(mod p),其中0≤n≤p-2,
所以s=n,即log(p)a(b c)=log(p)ab log(p)ac.
(3)证明 当b≥2时,由(2)可得bp-1≡1mod p,若b=1,则bp-1≡1mod p也成立.
因为n=log(p)ab,所以an≡b(mod p).
y2 ≡y2≡(x bk, )·(ak, )n(p-2)≡(xbk)akn(p-2)≡(xbk)bk(p-2)≡x(bp-1)k-1≡x(1)k-1(mod p)≡x(mod p).
因为x∈X,所以x=y2
同课章节目录
