第六章 平行四边形 单元检测(含答案)
文档属性
| 名称 | 第六章 平行四边形 单元检测(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 541.5KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-01-25 07:32:04 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
第六章 平行四边形
一、单选题
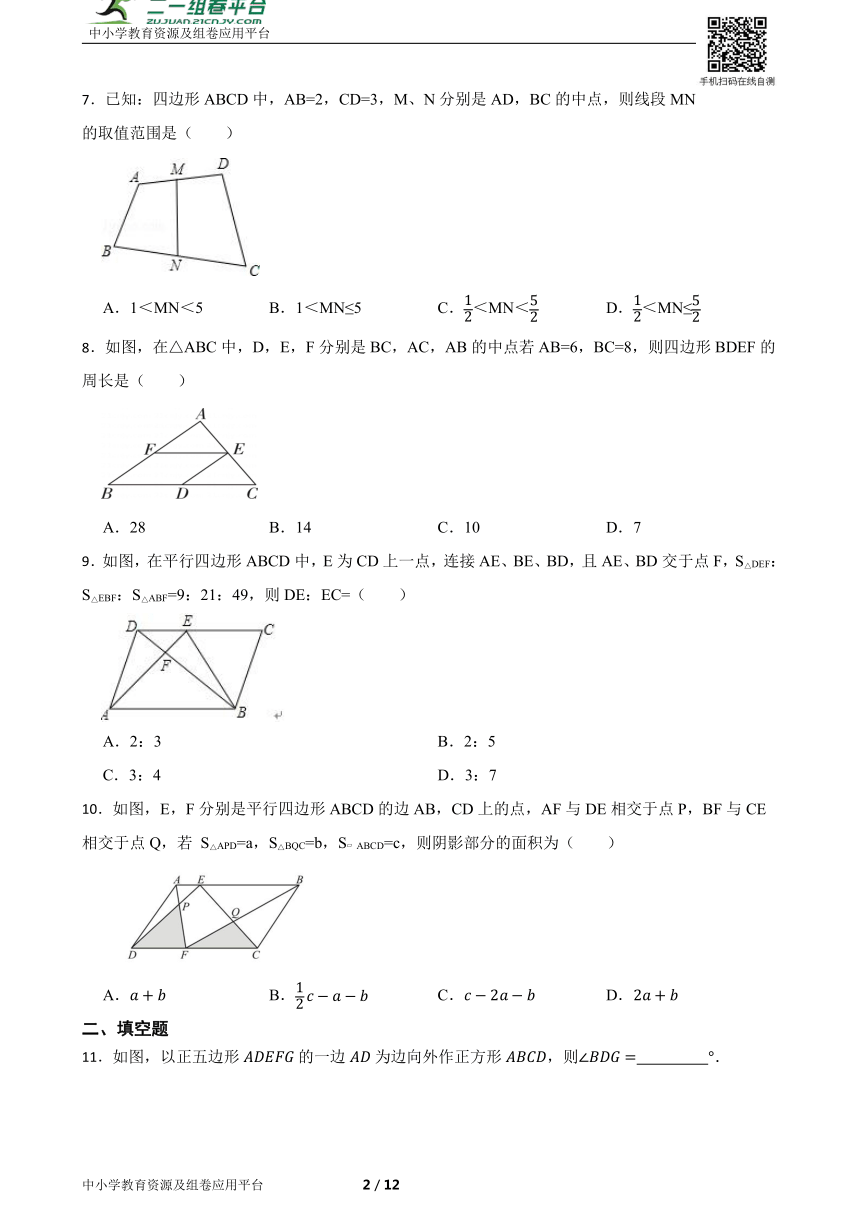
1.“花影遮墙,峰峦叠窗”苏州园林空透的窗棂中蕴含着许多的数学元素.如图是窗棂是冰裂纹窗及这种窗棂中的部分图案.若,,则下列判断中正确的是( )
A. B. C. D.
2.已知 ABCD中,∠A+∠C=80°,则∠B的度数为( )
A.80° B.100° C.120° D.140°
3.下列条件不能判定四边形ABCD是平行四边形的是( ).
A.AB∥CD, AD∥BC B.AD=BC, AB=CD
C.AB∥CD, AD=BC D.∠A=∠C , ∠B=∠D
4.如图,在平行四边形中,已知,,的平分线交边于点,则的长为( )
A.1 B.2 C.4 D.都不对
5.一个木匠有长的木材,他想用这些木材围绕花园苗床做一个护栏.他为花园苗床设计了如图所示的四种方案,其中不能实现的方案是( )
A. B.
C. D.
6.一个正多边形的内角和为,则这个正多边形的每一个外角的度数是( )
A. B. C. D.
7.已知:四边形ABCD中,AB=2,CD=3,M、N分别是AD,BC的中点,则线段MN的取值范围是( )
A.1<MN<5 B.1<MN≤5 C.<MN< D.<MN≤
8.如图,在△ABC中,D,E,F分别是BC,AC,AB的中点若AB=6,BC=8,则四边形BDEF的周长是( )
A.28 B.14 C.10 D.7
9.如图,在平行四边形ABCD中,E为CD上一点,连接AE、BE、BD,且AE、BD交于点F,S△DEF:S△EBF:S△ABF=9:21:49,则DE:EC=( )
A.2:3 B.2:5
C.3:4 D.3:7
10.如图,E,F分别是平行四边形ABCD的边AB,CD上的点,AF与DE相交于点P,BF与CE相交于点Q,若 S△APD=a,S△BQC=b,S ABCD=c,则阴影部分的面积为( )
A. B. C. D.
二、填空题
11.如图,以正五边形的一边为边向外作正方形,则 .
12.在平面直角坐标系中,平行四边形的顶点、、,则顶点的坐标是 .
13.如图,在与中,点,,分别是,,的中点,若的面积等于,则的面积为
14.如果一个多边形的每个外角都是40°,那么这个多边形是 边形.
15.若一个正多边形的每一个内角都等于120°,则它是正 边形.
16.如图,在 中,对角线,交于点,,,过点作的平分线的垂线,垂足为点,若点在的垂直平分线上,是直线上的动点,则的最小值为 .
三、计算题
17.(1)一个多边形的内角和是,求这个多边形共有多少条对角线.
(2)若一个正多边形的每一个内角都比与其相邻外角的3倍多,求这个多边形的边数.
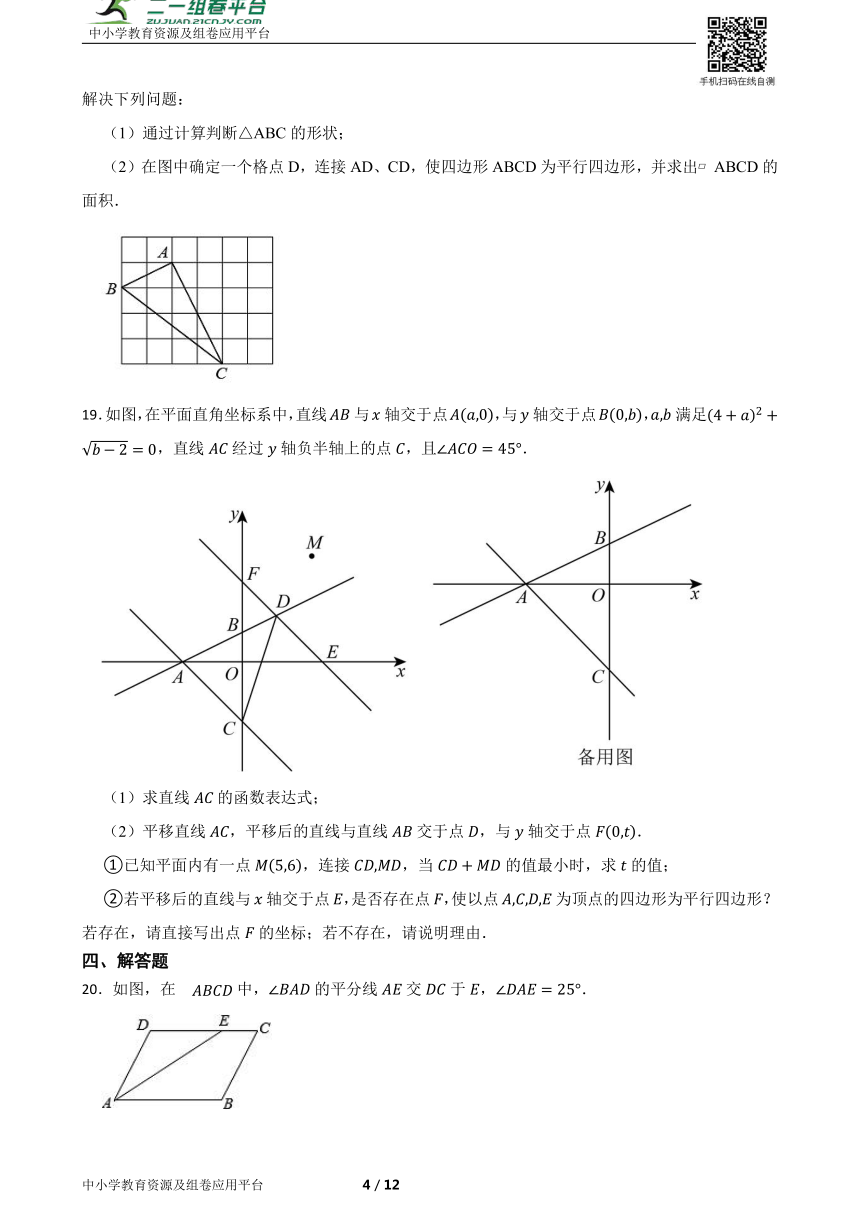
18.如图,在由边长为1的小正方形组成的5×6的网格中,△ABC的三个顶点均在格点上,请按要求解决下列问题:
(1)通过计算判断△ABC的形状;
(2)在图中确定一个格点D,连接AD、CD,使四边形ABCD为平行四边形,并求出 ABCD的面积.
19.如图,在平面直角坐标系中,直线与轴交于点,与轴交于点,满足,直线经过轴负半轴上的点,且.
(1)求直线的函数表达式;
(2)平移直线,平移后的直线与直线交于点,与轴交于点.
①已知平面内有一点,连接,当的值最小时,求的值;
②若平移后的直线与轴交于点,是否存在点,使以点为顶点的四边形为平行四边形?若存在,请直接写出点的坐标;若不存在,请说明理由.
四、解答题
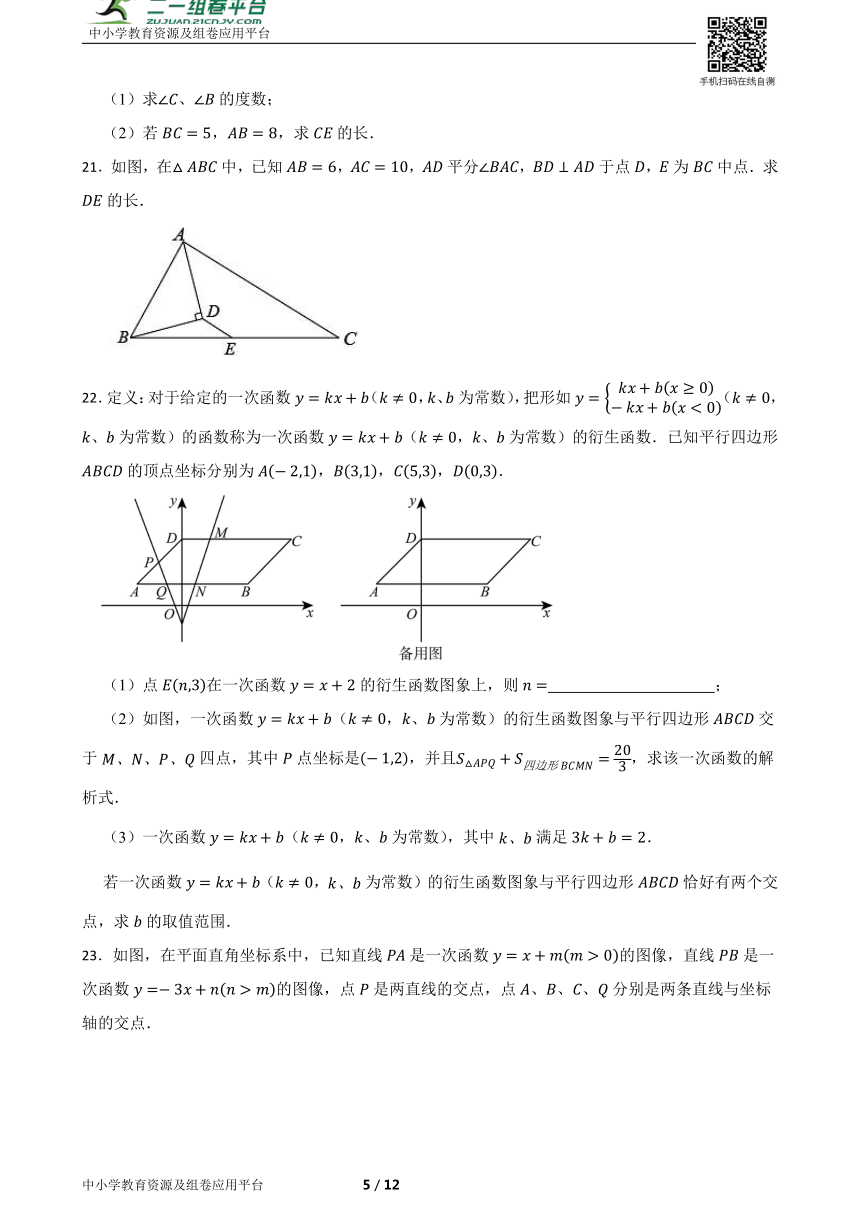
20.如图,在中,的平分线交于,.
(1)求、的度数;
(2)若,,求的长.
21.如图,在中,已知,,平分,于点,为中点.求的长.
22.定义:对于给定的一次函数(,、为常数),把形如(,、为常数)的函数称为一次函数(,、为常数)的衍生函数.已知平行四边形的顶点坐标分别为,,,.
(1)点在一次函数的衍生函数图象上,则 ;
(2)如图,一次函数(,、为常数)的衍生函数图象与平行四边形交于四点,其中点坐标是,并且,求该一次函数的解析式.
(3)一次函数(,、为常数),其中满足.
若一次函数(,为常数)的衍生函数图象与平行四边形恰好有两个交点,求的取值范围.
23.如图,在平面直角坐标系中,已知直线是一次函数的图像,直线是一次函数的图像,点是两直线的交点,点、、、分别是两条直线与坐标轴的交点.
(1)用、分别表示点、、的坐标;
(2)若四边形的面积是,且,试求点的坐标,并求出直线与的函数表达式;
(3)在(2)的条件下,是否存在一点,使以、、、为顶点的四边形是平行四边形?若存在,请直接写出点的坐标;若不存在,请说明理由.
答案解析部分
1.【答案】A
【知识点】多边形内角与外角
2.【答案】D
【知识点】平行四边形的性质
3.【答案】C
【知识点】平行四边形的判定
4.【答案】B
【知识点】角平分线的性质;等腰三角形的判定;平行四边形的性质
5.【答案】D
【知识点】平行四边形的性质;矩形的性质;生活中的旋转现象
6.【答案】A
【知识点】多边形内角与外角
7.【答案】D
【知识点】三角形三边关系;三角形的中位线定理
8.【答案】B
【知识点】平行四边形的判定与性质;三角形的中位线定理
9.【答案】C
【知识点】平行四边形的性质
10.【答案】B
【知识点】平行四边形的性质
11.【答案】81
【知识点】等腰三角形的性质;多边形内角与外角
12.【答案】
【知识点】平行四边形的性质;坐标与图形变化﹣平移
13.【答案】10
【知识点】三角形的中位线定理
14.【答案】九
【知识点】多边形内角与外角
15.【答案】6
【知识点】多边形内角与外角
16.【答案】
【知识点】平行四边形的性质;轴对称的应用-最短距离问题;线段垂直平分线的判定
17.【答案】(1)这个多边形共有27条对角线;(2)10
【知识点】多边形的对角线;多边形内角与外角
18.【答案】(1)△ABC是直角三角形;(2)□ABCD的面积为10.
【知识点】勾股定理;勾股定理的逆定理;平行四边形的判定
19.【答案】(1)解:∵,
而,,
∴,,
解得:,,
∴,,
∴,
∵,,
∴,
∴,
∴,
设直线的函数表达式为,
将点,代入表达式可得:
可得,
解得:,
∴直线的函数表达式为.
(2)解:①根据题意,平移直线,平移后的直线与直线交于点,与轴交于点,∴可设直线的函数表达式为;
设直线的函数表达式为,
将点,代入,
可得,
解得:,
∴直线的函数表达式为:;
如下图,连接,
∵,
∴当点在同一直线上时,取最小值,
此时,设直线的解析式为,
将点,代入MC的解析式得:
可得,
解得:,
∴直线的解析式为,
联立解方程组,
得:,
∴,
∴将点代入直线表达式,
可得,
解得:;
②(Ⅰ)当点在点右侧时,如下图,过点作轴于点,
∵四边形为平行四边形,
∴,,
∴,
在△AOC和△EMD中,
∴,
∴,即,
将代入直线的表达式,
可得,解得,
∴,
∴将点代入直线表达式,
可得,解得,即;
(Ⅱ)当点在点左侧时,如下图,过点作轴于点,
∵四边形为平行四边形,
∴,,
∴,
在△AOC和△E ND 中,
∴,
∴,即,
将代入直线的表达式,
可得,解得,
∴,
∴将点代入直线表达式,
可得,解得,即.
综上可得,点的坐标为或.
【知识点】待定系数法求一次函数解析式;两一次函数图象相交或平行问题;平行四边形的性质;一次函数中的动态几何问题;一次函数图象的平移变换
20.【答案】(1);
(2)
【知识点】平行线的性质;角平分线的性质;平行四边形的性质
21.【答案】2
【知识点】等腰三角形的判定;三角形的中位线定理
22.【答案】(1)
(2)
(3)或且
【知识点】一次函数的概念;待定系数法求一次函数解析式;平行四边形的性质;一次函数图象、性质与系数的关系
23.【答案】(1)A(-m,0), B(,0),P(,)
(2)PA的表达式为:
PB的表达式为:
(3)存在;D1,D2, D3.
【知识点】待定系数法求一次函数解析式;平行四边形的判定与性质;一次函数的实际应用-几何问题
中小学教育资源及组卷应用平台 1 / 12
第六章 平行四边形
一、单选题
1.“花影遮墙,峰峦叠窗”苏州园林空透的窗棂中蕴含着许多的数学元素.如图是窗棂是冰裂纹窗及这种窗棂中的部分图案.若,,则下列判断中正确的是( )
A. B. C. D.
2.已知 ABCD中,∠A+∠C=80°,则∠B的度数为( )
A.80° B.100° C.120° D.140°
3.下列条件不能判定四边形ABCD是平行四边形的是( ).
A.AB∥CD, AD∥BC B.AD=BC, AB=CD
C.AB∥CD, AD=BC D.∠A=∠C , ∠B=∠D
4.如图,在平行四边形中,已知,,的平分线交边于点,则的长为( )
A.1 B.2 C.4 D.都不对
5.一个木匠有长的木材,他想用这些木材围绕花园苗床做一个护栏.他为花园苗床设计了如图所示的四种方案,其中不能实现的方案是( )
A. B.
C. D.
6.一个正多边形的内角和为,则这个正多边形的每一个外角的度数是( )
A. B. C. D.
7.已知:四边形ABCD中,AB=2,CD=3,M、N分别是AD,BC的中点,则线段MN的取值范围是( )
A.1<MN<5 B.1<MN≤5 C.<MN< D.<MN≤
8.如图,在△ABC中,D,E,F分别是BC,AC,AB的中点若AB=6,BC=8,则四边形BDEF的周长是( )
A.28 B.14 C.10 D.7
9.如图,在平行四边形ABCD中,E为CD上一点,连接AE、BE、BD,且AE、BD交于点F,S△DEF:S△EBF:S△ABF=9:21:49,则DE:EC=( )
A.2:3 B.2:5
C.3:4 D.3:7
10.如图,E,F分别是平行四边形ABCD的边AB,CD上的点,AF与DE相交于点P,BF与CE相交于点Q,若 S△APD=a,S△BQC=b,S ABCD=c,则阴影部分的面积为( )
A. B. C. D.
二、填空题
11.如图,以正五边形的一边为边向外作正方形,则 .
12.在平面直角坐标系中,平行四边形的顶点、、,则顶点的坐标是 .
13.如图,在与中,点,,分别是,,的中点,若的面积等于,则的面积为
14.如果一个多边形的每个外角都是40°,那么这个多边形是 边形.
15.若一个正多边形的每一个内角都等于120°,则它是正 边形.
16.如图,在 中,对角线,交于点,,,过点作的平分线的垂线,垂足为点,若点在的垂直平分线上,是直线上的动点,则的最小值为 .
三、计算题
17.(1)一个多边形的内角和是,求这个多边形共有多少条对角线.
(2)若一个正多边形的每一个内角都比与其相邻外角的3倍多,求这个多边形的边数.
18.如图,在由边长为1的小正方形组成的5×6的网格中,△ABC的三个顶点均在格点上,请按要求解决下列问题:
(1)通过计算判断△ABC的形状;
(2)在图中确定一个格点D,连接AD、CD,使四边形ABCD为平行四边形,并求出 ABCD的面积.
19.如图,在平面直角坐标系中,直线与轴交于点,与轴交于点,满足,直线经过轴负半轴上的点,且.
(1)求直线的函数表达式;
(2)平移直线,平移后的直线与直线交于点,与轴交于点.
①已知平面内有一点,连接,当的值最小时,求的值;
②若平移后的直线与轴交于点,是否存在点,使以点为顶点的四边形为平行四边形?若存在,请直接写出点的坐标;若不存在,请说明理由.
四、解答题
20.如图,在中,的平分线交于,.
(1)求、的度数;
(2)若,,求的长.
21.如图,在中,已知,,平分,于点,为中点.求的长.
22.定义:对于给定的一次函数(,、为常数),把形如(,、为常数)的函数称为一次函数(,、为常数)的衍生函数.已知平行四边形的顶点坐标分别为,,,.
(1)点在一次函数的衍生函数图象上,则 ;
(2)如图,一次函数(,、为常数)的衍生函数图象与平行四边形交于四点,其中点坐标是,并且,求该一次函数的解析式.
(3)一次函数(,、为常数),其中满足.
若一次函数(,为常数)的衍生函数图象与平行四边形恰好有两个交点,求的取值范围.
23.如图,在平面直角坐标系中,已知直线是一次函数的图像,直线是一次函数的图像,点是两直线的交点,点、、、分别是两条直线与坐标轴的交点.
(1)用、分别表示点、、的坐标;
(2)若四边形的面积是,且,试求点的坐标,并求出直线与的函数表达式;
(3)在(2)的条件下,是否存在一点,使以、、、为顶点的四边形是平行四边形?若存在,请直接写出点的坐标;若不存在,请说明理由.
答案解析部分
1.【答案】A
【知识点】多边形内角与外角
2.【答案】D
【知识点】平行四边形的性质
3.【答案】C
【知识点】平行四边形的判定
4.【答案】B
【知识点】角平分线的性质;等腰三角形的判定;平行四边形的性质
5.【答案】D
【知识点】平行四边形的性质;矩形的性质;生活中的旋转现象
6.【答案】A
【知识点】多边形内角与外角
7.【答案】D
【知识点】三角形三边关系;三角形的中位线定理
8.【答案】B
【知识点】平行四边形的判定与性质;三角形的中位线定理
9.【答案】C
【知识点】平行四边形的性质
10.【答案】B
【知识点】平行四边形的性质
11.【答案】81
【知识点】等腰三角形的性质;多边形内角与外角
12.【答案】
【知识点】平行四边形的性质;坐标与图形变化﹣平移
13.【答案】10
【知识点】三角形的中位线定理
14.【答案】九
【知识点】多边形内角与外角
15.【答案】6
【知识点】多边形内角与外角
16.【答案】
【知识点】平行四边形的性质;轴对称的应用-最短距离问题;线段垂直平分线的判定
17.【答案】(1)这个多边形共有27条对角线;(2)10
【知识点】多边形的对角线;多边形内角与外角
18.【答案】(1)△ABC是直角三角形;(2)□ABCD的面积为10.
【知识点】勾股定理;勾股定理的逆定理;平行四边形的判定
19.【答案】(1)解:∵,
而,,
∴,,
解得:,,
∴,,
∴,
∵,,
∴,
∴,
∴,
设直线的函数表达式为,
将点,代入表达式可得:
可得,
解得:,
∴直线的函数表达式为.
(2)解:①根据题意,平移直线,平移后的直线与直线交于点,与轴交于点,∴可设直线的函数表达式为;
设直线的函数表达式为,
将点,代入,
可得,
解得:,
∴直线的函数表达式为:;
如下图,连接,
∵,
∴当点在同一直线上时,取最小值,
此时,设直线的解析式为,
将点,代入MC的解析式得:
可得,
解得:,
∴直线的解析式为,
联立解方程组,
得:,
∴,
∴将点代入直线表达式,
可得,
解得:;
②(Ⅰ)当点在点右侧时,如下图,过点作轴于点,
∵四边形为平行四边形,
∴,,
∴,
在△AOC和△EMD中,
∴,
∴,即,
将代入直线的表达式,
可得,解得,
∴,
∴将点代入直线表达式,
可得,解得,即;
(Ⅱ)当点在点左侧时,如下图,过点作轴于点,
∵四边形为平行四边形,
∴,,
∴,
在△AOC和△E ND 中,
∴,
∴,即,
将代入直线的表达式,
可得,解得,
∴,
∴将点代入直线表达式,
可得,解得,即.
综上可得,点的坐标为或.
【知识点】待定系数法求一次函数解析式;两一次函数图象相交或平行问题;平行四边形的性质;一次函数中的动态几何问题;一次函数图象的平移变换
20.【答案】(1);
(2)
【知识点】平行线的性质;角平分线的性质;平行四边形的性质
21.【答案】2
【知识点】等腰三角形的判定;三角形的中位线定理
22.【答案】(1)
(2)
(3)或且
【知识点】一次函数的概念;待定系数法求一次函数解析式;平行四边形的性质;一次函数图象、性质与系数的关系
23.【答案】(1)A(-m,0), B(,0),P(,)
(2)PA的表达式为:
PB的表达式为:
(3)存在;D1,D2, D3.
【知识点】待定系数法求一次函数解析式;平行四边形的判定与性质;一次函数的实际应用-几何问题
中小学教育资源及组卷应用平台 1 / 12
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
