北师版数学九下 2.3 确定二次函数的表达式 课件 (共33张PPT)
文档属性
| 名称 | 北师版数学九下 2.3 确定二次函数的表达式 课件 (共33张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-01-27 10:17:21 | ||
图片预览











文档简介
(共33张PPT)
第二章 二次函数 2.3
确定二次函数
的表达式
北师大版九年级下册数学课件
目录
目录
CONTENTS
CONTENTS
1-新知导入
2-探究新知
3-巩固练习
4-课堂小结
新知导入
第一部分
PART 01
your content is entered here, or by copying your text, select paste in this box and choose to retain only text. your content is typed here
复习引入
1. 一次函数 y = kx+b (k≠0) 有几个待定系数?通常需要已知几个点的坐标求出它的表达式?
2. 求一次函数表达式的方法是什么?它的一般步骤是什么?
2个
2个
待定系数法
(1)设:(表达式)
(2)代:(坐标代入)
(3)解:方程(组)
(4)还原:(写表达式)
∴
典例精析
例1 已知二次函数 y=ax2 + c 的图象经过点 (2,3)
和 (-1,-3),求这个二次函数的表达式.
解:∵该图象经过点(2,3)和(-1,-3),
3=4a+c,
-3=a+c,
∴所求二次函数表达式为 y=2x2-5.
a=2,
c=-5.
解得
{
关于 y 轴对称
{
特殊条件的二次函数的表达式
探究新知
第二部分
PART 02
your content is entered here, or by copying your text, select paste in this box and choose to retain only text. your content is typed here
1. 已知二次函数 y=ax2 + bx 的图象经过点(-2,8)
和(-1,5),求这个二次函数的表达式.
解:∵该图象经过点(-2,8)和(-1,5),
针对训练
图象经过
原点
8=4a-2b,
5=a-b,
∴
解得
∴ y=-x2-6x.
{
{
a= -1,
b= -6.
选取顶点(-2,1)和点(1,-8),试求出这个二次函数的表达式.
解:设这个二次函数的表达式是 y = a(x-h)2+k,把顶点(-2,1)代入 y=a(x-h)2+k 得
y = a(x+2)2+1,
再把点(1,-8)代入上式得
a(1+2)2+1= -8,
解得 a = -1.
∴所求的二次函数的表达式是 y= -(x+2)2+1或y= -x2-4x-3.
顶点法求二次函数的表达式
归纳总结
顶点法求二次函数的方法
这种知道抛物线的顶点坐标,求表达式的方法叫做顶点法.其步骤是:
① 设函数表达式为 y=a(x-h)2+k;
② 先代入顶点坐标,得到关于 a 的一元一次方程;
③ 将另一点的坐标代入原方程求出 a 值;
④ a 用数值换掉,写出函数表达式.
针对训练
2. 一个二次函数的图象经点 (0, 1),它的顶点坐标为(8,9),求这个二次函数的表达式.
解: 因为这个二次函数的图象的顶点坐标为(8,9),因此,可以设函数表达式为 y=a(x-8)2+9.
又由于它的图象经过点(0 ,1),可得 1= a(0-8)2+9.
解得
∴所求的二次函数的表达式是
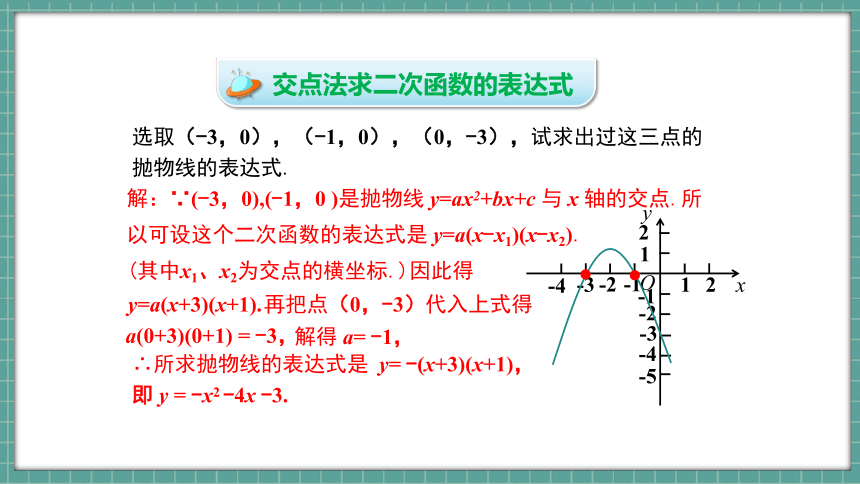
解:∵(-3,0),(-1,0 )是抛物线 y=ax2+bx+c 与 x 轴的交点.所以可设这个二次函数的表达式是 y=a(x-x1)(x-x2).
(其中x1、x2为交点的横坐标.)因此得
y=a(x+3)(x+1).
再把点(0,-3)代入上式得
a(0+3)(0+1) = -3,
解得 a= -1,
∴所求抛物线的表达式是 y= -(x+3)(x+1),
即 y = -x2 -4x -3.
选取(-3,0),(-1,0),(0,-3),试求出过这三点的抛物线的表达式.
x
y
O
1
2
-1
-2
-3
-4
-1
-2
-3
-4
-5
1
2
交点法求二次函数的表达式
归纳总结
交点法求二次函数表达式的方法
这种知道抛物线与 x 轴的交点,求表达式的方法叫做交点法.其步骤是:
① 设函数表达式是 y = a(x-x1)(x-x2);
② 先把两交点的横坐标 x1 , x2 代入到表达式中,得到关于 a 的一元一次方程;
③ 将另一点的坐标代入原方程求出 a 值;
④ a 用数值换掉,写出函数表达式.
想一想
确定二次函数的这三点应满足什么条件?
任意三点不在同一直线上(其中两点的连线可平行于x轴,但不可以平行于y轴.
合作探究
问题1 (1)二次函数 y = ax2+bx+c (a≠0) 中有几个待定系数?需要几个抛物线上的点的坐标才能求出来?
3个
3个
(2)下面是我们用描点法画二次函数的图象所列表格的一部分:
x -3 -2 -1 0 1 2
y 0 1 0 -3 -8 -15
一般式法求二次函数的表达式
解: 设这个二次函数的表达式是y=ax2+bx+c,把(-3,0),(-1,0),(0,-3)代入 y=ax2+bx+c 得
①选取(-3,0),(-1,0),(0,-3)
试求出这个二次函数的表达式.
9a-3b+c=0,
a-b+c=0,
c= -3,
解得
a = -1,
b = -4,
c = -3.
∴所求的二次函数的表达式是 y=-x2-4x-3.
待定系数法
步骤:
1.设:
(表达式)
2.代:
(坐标代入)
3.解:
方程(组)
4.还原:
(写表达式)
典例精析
例2 已知二次函数的图象经过点(-1,10),(1,4),(2,7) 三点,求这个二次函数的表达式,并写出它的对称轴和顶点坐标.
解: 设所求二次函数的表达式为 y = ax2+bx+c.
∵该图象经过点(-1,10),(1,4),(2,7),
a = 2,
∴
10 = a-b+c,
7 = 4a+2b+c,
c = 5.
解得
4 = a+b+c
b = -3,
∴二次函数图像对称轴为直线 ,
顶点坐标为 .
∴所求二次函数表达式为
这种已知三点求二次函数表达式的方法叫做一般式法.
其步骤是:
① 设函数表达式为 y = ax2+bx+c;
② 代入后得到一个三元一次方程组;
③ 解方程组得到 a,b,c 的值;
④ 把待定系数用数字换掉,写出函数表达式.
归纳总结
一般式法求二次函数表达式的方法
巩固练习
第三部分
PART 03
your content is entered here, or by copying your text, select paste in this box and choose to retain only text. your content is typed here
针对训练
3. 一个二次函数的图象经过 (0, 1)、(2,4)、(3,10) 三点,求这个二次函数的表达式.
解: 设这个二次函数的表达式是 y=ax2+bx+c,由于这个函数经过点(0, 1),可得 c=1.
又由于其图象经过(2,4)、(3,10)两点,可得
4a+2b+1=4,
9a+3b+1=10,
解这个方程组,得
∴所求的二次函数的表达式是
1. 如图,平面直角坐标系中,函数图象的表达式应是 .
注 y=ax2 与 y=ax2+k、y=a(x-h)2、y=a(x-h)2+k 一样都是顶点式,只不过前三者是顶点式的特殊形式.
注意
x
y
O
1
2
-1
-2
-3
-4
2
1
-1
3
4
5
2. 过点(2,4),且当 x=1 时,y 有最值为 6,则其表达式是 .
顶点坐标是(1,6)
y = -2(x-1)2+6
3. 已知二次函数的图象经过点(-1,-5),(0,-4)和(1,1).求这个二次函数的表达式.
解:设这个二次函数的表达式为y=ax2+bx+c.
依题意得
∴这个二次函数的表达式为 y=2x2+3x-4.
a+b+c=1,
c=-4,
a-b+c=-5,
解得
b=3,
c=-4,
a=2,
4. 已知抛物线与x轴相交于点 A(-1,0),B(1,0),且过点 M(0,1),求此函数的表达式.
解:因为点A(-1,0),B(1,0)是图象与 x 轴的交点,所以设二次函数的表达式为 y=a(x+1)(x-1).
又因为抛物线过点 M(0,1),
所以1=a(0+1)(0-1),解得 a=-1,
所以所求抛物线的表达式为 y=-(x+1)(x-1),
即 y=-x2+1.
5. 综合题:如图,已知二次函数 的图象经过 A(2,0),B(0,-6) 两点.
(1) 求这个二次函数的表达式;
A
B
C
x
y
O
解:∵该图象经过点(2,0)和(1,-6),
{
-2+2b+c=0
c=-6
解得
{
b=4
c=-6
∴二次函数的表达式为:
(2) 设该二次函数的对称轴与x轴交于点 C,连接BA,BC,求 △ABC 的积.
A
B
C
x
y
O
解:∵二次函数对称轴为
∴c点坐标为(2,0).
6.已知一条抛物线经过 E(0,10),F(2,2),G(4,2),H(3,1)四点,选择其中两点用待定系数法能求出抛物线解析式的为( )
A.E,F
B.E,G
C.E,H
D.F,G
C
7.如果抛物线 y = x2-6x+c-2 的顶点到 x 轴的距离是3,那么 c 的值等于( )
A. 8
B. 14
C. 8或14
D. -8或-14
C
8. 如图,抛物线 y=x2+bx+c 过点 A(-4,-3),与 y轴交于点 B ,对称轴是 x=-3,请解答下列问题:
(1) 求抛物线的表达式;
解:把点A(-4,-3)代入 y=x2+bx+c
得16-4b+c=-3,c-4b=-19.
∵对称轴是x=-3,∴ =-3,
∴b=6,∴c=5,
∴抛物线的表达式是 y=x2+6x+5.
(2) 若和 x 轴平行的直线与抛物线交于 C,D 两点,点 C 在对称轴左侧,且 CD=8,求 △BCD 的面积.
∵CD∥x 轴,∴点 C 与点 D 关于 x=-3 对称.
∵点 C 在对称轴左侧,且 CD=8,
∴点 C 的横坐标为-7,
∴点 C 的纵坐标为(-7)2+6×(-7)+5=12.
∵点 B 的坐标为(0,5),
∴△BCD 中 CD 边上的高为12-5=7,
∴△BCD 的面积= ×8×7=28.
课堂小结
第四部分
PART 04
your content is entered here, or by copying your text, select paste in this box and choose to retain only text. your content is typed here
①已知三点坐标
②已知顶点坐标或对称轴或最值
③已知抛物线与x轴的两个交点
已知条件
所选方法
用一般式法:y = ax2+bx+c
用顶点法:y = a(x-h)2+k
用交点法:y = a(x-x1)(x-x2)
(x1,x2为交点的横坐标)
待定系数法
求二次函数解析式
第二章 二次函数 2.3
确定二次函数
的表达式
北师大版九年级下册数学课件
第二章 二次函数 2.3
确定二次函数
的表达式
北师大版九年级下册数学课件
目录
目录
CONTENTS
CONTENTS
1-新知导入
2-探究新知
3-巩固练习
4-课堂小结
新知导入
第一部分
PART 01
your content is entered here, or by copying your text, select paste in this box and choose to retain only text. your content is typed here
复习引入
1. 一次函数 y = kx+b (k≠0) 有几个待定系数?通常需要已知几个点的坐标求出它的表达式?
2. 求一次函数表达式的方法是什么?它的一般步骤是什么?
2个
2个
待定系数法
(1)设:(表达式)
(2)代:(坐标代入)
(3)解:方程(组)
(4)还原:(写表达式)
∴
典例精析
例1 已知二次函数 y=ax2 + c 的图象经过点 (2,3)
和 (-1,-3),求这个二次函数的表达式.
解:∵该图象经过点(2,3)和(-1,-3),
3=4a+c,
-3=a+c,
∴所求二次函数表达式为 y=2x2-5.
a=2,
c=-5.
解得
{
关于 y 轴对称
{
特殊条件的二次函数的表达式
探究新知
第二部分
PART 02
your content is entered here, or by copying your text, select paste in this box and choose to retain only text. your content is typed here
1. 已知二次函数 y=ax2 + bx 的图象经过点(-2,8)
和(-1,5),求这个二次函数的表达式.
解:∵该图象经过点(-2,8)和(-1,5),
针对训练
图象经过
原点
8=4a-2b,
5=a-b,
∴
解得
∴ y=-x2-6x.
{
{
a= -1,
b= -6.
选取顶点(-2,1)和点(1,-8),试求出这个二次函数的表达式.
解:设这个二次函数的表达式是 y = a(x-h)2+k,把顶点(-2,1)代入 y=a(x-h)2+k 得
y = a(x+2)2+1,
再把点(1,-8)代入上式得
a(1+2)2+1= -8,
解得 a = -1.
∴所求的二次函数的表达式是 y= -(x+2)2+1或y= -x2-4x-3.
顶点法求二次函数的表达式
归纳总结
顶点法求二次函数的方法
这种知道抛物线的顶点坐标,求表达式的方法叫做顶点法.其步骤是:
① 设函数表达式为 y=a(x-h)2+k;
② 先代入顶点坐标,得到关于 a 的一元一次方程;
③ 将另一点的坐标代入原方程求出 a 值;
④ a 用数值换掉,写出函数表达式.
针对训练
2. 一个二次函数的图象经点 (0, 1),它的顶点坐标为(8,9),求这个二次函数的表达式.
解: 因为这个二次函数的图象的顶点坐标为(8,9),因此,可以设函数表达式为 y=a(x-8)2+9.
又由于它的图象经过点(0 ,1),可得 1= a(0-8)2+9.
解得
∴所求的二次函数的表达式是
解:∵(-3,0),(-1,0 )是抛物线 y=ax2+bx+c 与 x 轴的交点.所以可设这个二次函数的表达式是 y=a(x-x1)(x-x2).
(其中x1、x2为交点的横坐标.)因此得
y=a(x+3)(x+1).
再把点(0,-3)代入上式得
a(0+3)(0+1) = -3,
解得 a= -1,
∴所求抛物线的表达式是 y= -(x+3)(x+1),
即 y = -x2 -4x -3.
选取(-3,0),(-1,0),(0,-3),试求出过这三点的抛物线的表达式.
x
y
O
1
2
-1
-2
-3
-4
-1
-2
-3
-4
-5
1
2
交点法求二次函数的表达式
归纳总结
交点法求二次函数表达式的方法
这种知道抛物线与 x 轴的交点,求表达式的方法叫做交点法.其步骤是:
① 设函数表达式是 y = a(x-x1)(x-x2);
② 先把两交点的横坐标 x1 , x2 代入到表达式中,得到关于 a 的一元一次方程;
③ 将另一点的坐标代入原方程求出 a 值;
④ a 用数值换掉,写出函数表达式.
想一想
确定二次函数的这三点应满足什么条件?
任意三点不在同一直线上(其中两点的连线可平行于x轴,但不可以平行于y轴.
合作探究
问题1 (1)二次函数 y = ax2+bx+c (a≠0) 中有几个待定系数?需要几个抛物线上的点的坐标才能求出来?
3个
3个
(2)下面是我们用描点法画二次函数的图象所列表格的一部分:
x -3 -2 -1 0 1 2
y 0 1 0 -3 -8 -15
一般式法求二次函数的表达式
解: 设这个二次函数的表达式是y=ax2+bx+c,把(-3,0),(-1,0),(0,-3)代入 y=ax2+bx+c 得
①选取(-3,0),(-1,0),(0,-3)
试求出这个二次函数的表达式.
9a-3b+c=0,
a-b+c=0,
c= -3,
解得
a = -1,
b = -4,
c = -3.
∴所求的二次函数的表达式是 y=-x2-4x-3.
待定系数法
步骤:
1.设:
(表达式)
2.代:
(坐标代入)
3.解:
方程(组)
4.还原:
(写表达式)
典例精析
例2 已知二次函数的图象经过点(-1,10),(1,4),(2,7) 三点,求这个二次函数的表达式,并写出它的对称轴和顶点坐标.
解: 设所求二次函数的表达式为 y = ax2+bx+c.
∵该图象经过点(-1,10),(1,4),(2,7),
a = 2,
∴
10 = a-b+c,
7 = 4a+2b+c,
c = 5.
解得
4 = a+b+c
b = -3,
∴二次函数图像对称轴为直线 ,
顶点坐标为 .
∴所求二次函数表达式为
这种已知三点求二次函数表达式的方法叫做一般式法.
其步骤是:
① 设函数表达式为 y = ax2+bx+c;
② 代入后得到一个三元一次方程组;
③ 解方程组得到 a,b,c 的值;
④ 把待定系数用数字换掉,写出函数表达式.
归纳总结
一般式法求二次函数表达式的方法
巩固练习
第三部分
PART 03
your content is entered here, or by copying your text, select paste in this box and choose to retain only text. your content is typed here
针对训练
3. 一个二次函数的图象经过 (0, 1)、(2,4)、(3,10) 三点,求这个二次函数的表达式.
解: 设这个二次函数的表达式是 y=ax2+bx+c,由于这个函数经过点(0, 1),可得 c=1.
又由于其图象经过(2,4)、(3,10)两点,可得
4a+2b+1=4,
9a+3b+1=10,
解这个方程组,得
∴所求的二次函数的表达式是
1. 如图,平面直角坐标系中,函数图象的表达式应是 .
注 y=ax2 与 y=ax2+k、y=a(x-h)2、y=a(x-h)2+k 一样都是顶点式,只不过前三者是顶点式的特殊形式.
注意
x
y
O
1
2
-1
-2
-3
-4
2
1
-1
3
4
5
2. 过点(2,4),且当 x=1 时,y 有最值为 6,则其表达式是 .
顶点坐标是(1,6)
y = -2(x-1)2+6
3. 已知二次函数的图象经过点(-1,-5),(0,-4)和(1,1).求这个二次函数的表达式.
解:设这个二次函数的表达式为y=ax2+bx+c.
依题意得
∴这个二次函数的表达式为 y=2x2+3x-4.
a+b+c=1,
c=-4,
a-b+c=-5,
解得
b=3,
c=-4,
a=2,
4. 已知抛物线与x轴相交于点 A(-1,0),B(1,0),且过点 M(0,1),求此函数的表达式.
解:因为点A(-1,0),B(1,0)是图象与 x 轴的交点,所以设二次函数的表达式为 y=a(x+1)(x-1).
又因为抛物线过点 M(0,1),
所以1=a(0+1)(0-1),解得 a=-1,
所以所求抛物线的表达式为 y=-(x+1)(x-1),
即 y=-x2+1.
5. 综合题:如图,已知二次函数 的图象经过 A(2,0),B(0,-6) 两点.
(1) 求这个二次函数的表达式;
A
B
C
x
y
O
解:∵该图象经过点(2,0)和(1,-6),
{
-2+2b+c=0
c=-6
解得
{
b=4
c=-6
∴二次函数的表达式为:
(2) 设该二次函数的对称轴与x轴交于点 C,连接BA,BC,求 △ABC 的积.
A
B
C
x
y
O
解:∵二次函数对称轴为
∴c点坐标为(2,0).
6.已知一条抛物线经过 E(0,10),F(2,2),G(4,2),H(3,1)四点,选择其中两点用待定系数法能求出抛物线解析式的为( )
A.E,F
B.E,G
C.E,H
D.F,G
C
7.如果抛物线 y = x2-6x+c-2 的顶点到 x 轴的距离是3,那么 c 的值等于( )
A. 8
B. 14
C. 8或14
D. -8或-14
C
8. 如图,抛物线 y=x2+bx+c 过点 A(-4,-3),与 y轴交于点 B ,对称轴是 x=-3,请解答下列问题:
(1) 求抛物线的表达式;
解:把点A(-4,-3)代入 y=x2+bx+c
得16-4b+c=-3,c-4b=-19.
∵对称轴是x=-3,∴ =-3,
∴b=6,∴c=5,
∴抛物线的表达式是 y=x2+6x+5.
(2) 若和 x 轴平行的直线与抛物线交于 C,D 两点,点 C 在对称轴左侧,且 CD=8,求 △BCD 的面积.
∵CD∥x 轴,∴点 C 与点 D 关于 x=-3 对称.
∵点 C 在对称轴左侧,且 CD=8,
∴点 C 的横坐标为-7,
∴点 C 的纵坐标为(-7)2+6×(-7)+5=12.
∵点 B 的坐标为(0,5),
∴△BCD 中 CD 边上的高为12-5=7,
∴△BCD 的面积= ×8×7=28.
课堂小结
第四部分
PART 04
your content is entered here, or by copying your text, select paste in this box and choose to retain only text. your content is typed here
①已知三点坐标
②已知顶点坐标或对称轴或最值
③已知抛物线与x轴的两个交点
已知条件
所选方法
用一般式法:y = ax2+bx+c
用顶点法:y = a(x-h)2+k
用交点法:y = a(x-x1)(x-x2)
(x1,x2为交点的横坐标)
待定系数法
求二次函数解析式
第二章 二次函数 2.3
确定二次函数
的表达式
北师大版九年级下册数学课件
