北师版数学九下 1.6利用三角函数测高 课件(共27张PPT)
文档属性
| 名称 | 北师版数学九下 1.6利用三角函数测高 课件(共27张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-01-27 10:20:12 | ||
图片预览








文档简介
(共27张PPT)
第一章 直角三角形的边角关系 1.6
利用三角
函数测高
北师大版九年级下册数学课件
目录
目录
CONTENTS
CONTENTS
1-新知导入
2-探究新知
3-巩固练习
4-课堂小结
新知导入
第一部分
PART 01
your content is entered here, or by copying your text, select paste in this box and choose to retain only text. your content is typed here
如果不告诉你这些高楼大厦的高度,你能想到办法测出它们的高度吗?
通过这节课的学习,相信你就行.
情境引入
0
30
30
60
60
90
90
P
Q
度盘
铅锤
支杆
问题1:如何测量倾斜角?
测量倾斜角可以用测倾器,
----简单的侧倾器由度盘、铅锤和支杆组成
测量倾斜角
0
30
30
60
60
90
90
1.把支架竖直插入地面,使支架的中心线、铅垂线和度盘的 0° 刻度线重合,这时度盘的顶线 PQ 在水平位置.
问题2:如何使用测倾器?
P
Q
M
0
30
30
60
60
06
90
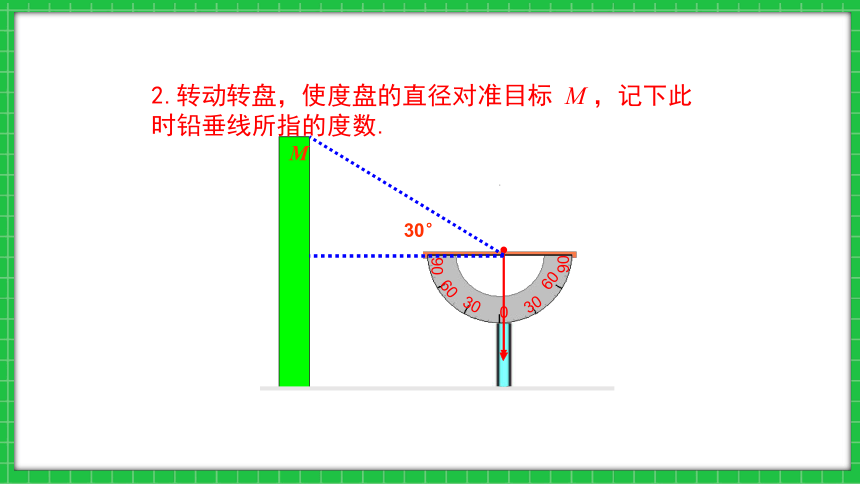
2.转动转盘,使度盘的直径对准目标 M ,记下此时铅垂线所指的度数.
30°
问题1:如何测量旗杆的高度?
A
C
M
N
E
在现实生活中,我们可以直接在旗杆下来回行走,所以只需测量一次角度(如图中的 α )就可以确定旗杆的高度.
α
所谓“底部可以到达”,就是在地面上可以无障碍地直接测得测点与被测物体的底部之间的距离,如图 CE 的长度.
测量底部可以到达的物体的高度
A
C
M
N
1. 在测点A安置测倾器,测得M的仰角 ∠MCE = α ;
E
2. 量出测点A到物体底部N的水平距离 AN = l ;
3. 量出测倾器的高度 AC = a ,可求出 MN 的高度.
MN = ME + EN = l·tanα + a
α
问题2:测量旗杆的高度的步骤是怎么样的呢?
探究新知
第二部分
PART 02
your content is entered here, or by copying your text, select paste in this box and choose to retain only text. your content is typed here
例1 如图,某中学在主楼的顶部和大门的上方之间挂一些彩旗.经测量,得到大门的高度是 5m,大门距主楼的距离是 30m,在大门处测得主楼顶部的仰角是 30°,而当时侧倾器离地面 1.4m,求学校主楼的高度(精确到
0.01m).
典例精析
解:如图,作 EM 垂直 CD 于 M 点,根据题意,可知
∠DEM = 30°,BC = EM = 30m,
CM = BE = 1.4m
M
在 Rt△DEM 中,
DM = EM tan30° ≈ 30×0.577 = 17.32 (m),
CD = DM + CM = 17.32+1.4 ≈ 18.72 (m).
∴学校主楼的高度约为 18.72 m
问题 1:在黄浦江的另一端,你能测量东方明珠的高度呢?
所谓“底部不可以到达”,就是在地面上不能直接测得测点与被测物体的底部之间的距离,如图中的 AN或 BN 的长度.
A
C
B
D
M
N
E
α
β
在现实生活中,我们不可以直接从测点到达被测点的脚下,这时我们能利用两次测量仰角(图中 α 和 β ),再结合解三角形的知识来求出东方明珠的高度.
测量底部不可以到达的物体的高度
问题 2:测量东方明珠的高度的步骤是怎么样的呢?
1. 在测点 A 处安置测倾器,测得此时 M 的仰角∠MCE=α;
A
C
B
D
M
N
E
α
2. 在测点 A 与物体之间的 B 处安置测倾器,测得此时
M 的仰角 ∠MDE = β;
β
3. 量出测倾器的高度 AC = BD = a,以及测点 A,B 之间的距离 AB = b .根据测量数据,可求出物体 MN 的高度.
课题 在平面上测量地王大厦的高 AB 测量示意图 测得数据 (测倾器高度为1m) 测量项目 ∠α ∠β CD 的长
第一次 30°16' 45° 5' 60.11 m
第二次 29°44' 44°25’' 59.89 m
平均值
例2 下表是小亮所填实习报告的部分内容,请根据数据求大楼的高.
C
E
D
F
A
G
B
α
β
30°
45°
60 m
解:由表格中数据,得α = 30° ,β = 45°,
答:大楼高度为 .
1.如图所示,在离上海东方明珠塔 1000 m 的 A 处,用仪器测得塔顶的仰角 ∠BAC为 25° (在视线与水平线所成的角中,视线在水平线上方的叫作仰角,在水平线下方的叫作俯角),仪器距地面高为 1.7 m.求上海东方明珠塔的高 BD.(结果精确到 1m .)
解:如图,在 Rt△ABC 中,∠BAC = 25°,AC = 1000 m,
答:上海东方明珠塔的高度 BD 为 468m.
从而 BC = 1000×tan25°≈ 466.3 (m).
因此,上海东方明珠塔的高度
BD = 466.3+1.7 ≈ 468 (m)
因此
巩固练习
第三部分
PART 03
your content is entered here, or by copying your text, select paste in this box and choose to retain only text. your content is typed here
2.如图,小明想测量塔 AB 的高度.他在 D 处仰望塔顶,测得仰角为 30°,再往塔的方向前进 50 m 至 C 处.测得仰角为 60°,小明的身高为 1.5 m. 你能帮小明算出该塔有多高吗 (结果精确到 1 m)
D′
A
B′
B
D
C′
C
解:如图,由题意可知,∠AD′B′=30°,∠AC′B′=60°, D′C′=50m.
∴ ∠D′AB′=60°,∠C′AB′=30°,D′C′=50m ,
设AB′=x m
D′
A
B′
B
D
C′
C
解:(1)由题意,AC=AB=610(米);
(2)DE=AC=610(米),
在Rt△BDE中,tan∠BDE=
故BE=DE tan39°. 因为 CD=AE,所以
CD=AB-DE·tan39°=610-610×tan39°≈116(米)
3.目前世界上最高的电视塔是广州新电视塔.如图所示,新电视塔高 AB 为 610 米,远处有一栋大楼,某人在楼底 C 处测得塔顶 B 的仰角为 45°,在楼顶 D 处测得塔顶 B 的仰角为 39°.(tan39° ≈ 0.81)
(1)求大楼与电视塔之间的距离 AC;
(2)求大楼的高度 CD(精确到 1 米)
(参考数据: )
4. 小明家所在居民楼的对面有一座大厦 AB,AB=80米.为测量居民楼与这座大厦之间的距离,小明从自己家的窗户 C 处测得大厦顶部 A 的仰角为 37°,大厦底部 B 的俯角为 48°.求小明家所在居民楼与大厦的距离 CD 的长度.(结果保留整数)
∵AD+BD = AB,
∴
解:设 CD = x 米.在 Rt△ACD 中,
在 Rt△BCD,tan48°=
解得:x ≈ 43.
答:小明家所在居民楼与大厦的距离 CD 大约是 43 米.
则
则
课堂小结
第四部分
PART 04
your content is entered here, or by copying your text, select paste in this box and choose to retain only text. your content is typed here
利用三角函数测高
测倾器的认识及使用
测量底部可以到达的物体的高度(一次测量仰角)
测量底部不可以到达的物体的高度(两次测量仰角)
利用解三角形的知识,求出物体的高度
第一章 直角三角形的边角关系 1.6
利用三角
函数测高
北师大版九年级下册数学课件
第一章 直角三角形的边角关系 1.6
利用三角
函数测高
北师大版九年级下册数学课件
目录
目录
CONTENTS
CONTENTS
1-新知导入
2-探究新知
3-巩固练习
4-课堂小结
新知导入
第一部分
PART 01
your content is entered here, or by copying your text, select paste in this box and choose to retain only text. your content is typed here
如果不告诉你这些高楼大厦的高度,你能想到办法测出它们的高度吗?
通过这节课的学习,相信你就行.
情境引入
0
30
30
60
60
90
90
P
Q
度盘
铅锤
支杆
问题1:如何测量倾斜角?
测量倾斜角可以用测倾器,
----简单的侧倾器由度盘、铅锤和支杆组成
测量倾斜角
0
30
30
60
60
90
90
1.把支架竖直插入地面,使支架的中心线、铅垂线和度盘的 0° 刻度线重合,这时度盘的顶线 PQ 在水平位置.
问题2:如何使用测倾器?
P
Q
M
0
30
30
60
60
06
90
2.转动转盘,使度盘的直径对准目标 M ,记下此时铅垂线所指的度数.
30°
问题1:如何测量旗杆的高度?
A
C
M
N
E
在现实生活中,我们可以直接在旗杆下来回行走,所以只需测量一次角度(如图中的 α )就可以确定旗杆的高度.
α
所谓“底部可以到达”,就是在地面上可以无障碍地直接测得测点与被测物体的底部之间的距离,如图 CE 的长度.
测量底部可以到达的物体的高度
A
C
M
N
1. 在测点A安置测倾器,测得M的仰角 ∠MCE = α ;
E
2. 量出测点A到物体底部N的水平距离 AN = l ;
3. 量出测倾器的高度 AC = a ,可求出 MN 的高度.
MN = ME + EN = l·tanα + a
α
问题2:测量旗杆的高度的步骤是怎么样的呢?
探究新知
第二部分
PART 02
your content is entered here, or by copying your text, select paste in this box and choose to retain only text. your content is typed here
例1 如图,某中学在主楼的顶部和大门的上方之间挂一些彩旗.经测量,得到大门的高度是 5m,大门距主楼的距离是 30m,在大门处测得主楼顶部的仰角是 30°,而当时侧倾器离地面 1.4m,求学校主楼的高度(精确到
0.01m).
典例精析
解:如图,作 EM 垂直 CD 于 M 点,根据题意,可知
∠DEM = 30°,BC = EM = 30m,
CM = BE = 1.4m
M
在 Rt△DEM 中,
DM = EM tan30° ≈ 30×0.577 = 17.32 (m),
CD = DM + CM = 17.32+1.4 ≈ 18.72 (m).
∴学校主楼的高度约为 18.72 m
问题 1:在黄浦江的另一端,你能测量东方明珠的高度呢?
所谓“底部不可以到达”,就是在地面上不能直接测得测点与被测物体的底部之间的距离,如图中的 AN或 BN 的长度.
A
C
B
D
M
N
E
α
β
在现实生活中,我们不可以直接从测点到达被测点的脚下,这时我们能利用两次测量仰角(图中 α 和 β ),再结合解三角形的知识来求出东方明珠的高度.
测量底部不可以到达的物体的高度
问题 2:测量东方明珠的高度的步骤是怎么样的呢?
1. 在测点 A 处安置测倾器,测得此时 M 的仰角∠MCE=α;
A
C
B
D
M
N
E
α
2. 在测点 A 与物体之间的 B 处安置测倾器,测得此时
M 的仰角 ∠MDE = β;
β
3. 量出测倾器的高度 AC = BD = a,以及测点 A,B 之间的距离 AB = b .根据测量数据,可求出物体 MN 的高度.
课题 在平面上测量地王大厦的高 AB 测量示意图 测得数据 (测倾器高度为1m) 测量项目 ∠α ∠β CD 的长
第一次 30°16' 45° 5' 60.11 m
第二次 29°44' 44°25’' 59.89 m
平均值
例2 下表是小亮所填实习报告的部分内容,请根据数据求大楼的高.
C
E
D
F
A
G
B
α
β
30°
45°
60 m
解:由表格中数据,得α = 30° ,β = 45°,
答:大楼高度为 .
1.如图所示,在离上海东方明珠塔 1000 m 的 A 处,用仪器测得塔顶的仰角 ∠BAC为 25° (在视线与水平线所成的角中,视线在水平线上方的叫作仰角,在水平线下方的叫作俯角),仪器距地面高为 1.7 m.求上海东方明珠塔的高 BD.(结果精确到 1m .)
解:如图,在 Rt△ABC 中,∠BAC = 25°,AC = 1000 m,
答:上海东方明珠塔的高度 BD 为 468m.
从而 BC = 1000×tan25°≈ 466.3 (m).
因此,上海东方明珠塔的高度
BD = 466.3+1.7 ≈ 468 (m)
因此
巩固练习
第三部分
PART 03
your content is entered here, or by copying your text, select paste in this box and choose to retain only text. your content is typed here
2.如图,小明想测量塔 AB 的高度.他在 D 处仰望塔顶,测得仰角为 30°,再往塔的方向前进 50 m 至 C 处.测得仰角为 60°,小明的身高为 1.5 m. 你能帮小明算出该塔有多高吗 (结果精确到 1 m)
D′
A
B′
B
D
C′
C
解:如图,由题意可知,∠AD′B′=30°,∠AC′B′=60°, D′C′=50m.
∴ ∠D′AB′=60°,∠C′AB′=30°,D′C′=50m ,
设AB′=x m
D′
A
B′
B
D
C′
C
解:(1)由题意,AC=AB=610(米);
(2)DE=AC=610(米),
在Rt△BDE中,tan∠BDE=
故BE=DE tan39°. 因为 CD=AE,所以
CD=AB-DE·tan39°=610-610×tan39°≈116(米)
3.目前世界上最高的电视塔是广州新电视塔.如图所示,新电视塔高 AB 为 610 米,远处有一栋大楼,某人在楼底 C 处测得塔顶 B 的仰角为 45°,在楼顶 D 处测得塔顶 B 的仰角为 39°.(tan39° ≈ 0.81)
(1)求大楼与电视塔之间的距离 AC;
(2)求大楼的高度 CD(精确到 1 米)
(参考数据: )
4. 小明家所在居民楼的对面有一座大厦 AB,AB=80米.为测量居民楼与这座大厦之间的距离,小明从自己家的窗户 C 处测得大厦顶部 A 的仰角为 37°,大厦底部 B 的俯角为 48°.求小明家所在居民楼与大厦的距离 CD 的长度.(结果保留整数)
∵AD+BD = AB,
∴
解:设 CD = x 米.在 Rt△ACD 中,
在 Rt△BCD,tan48°=
解得:x ≈ 43.
答:小明家所在居民楼与大厦的距离 CD 大约是 43 米.
则
则
课堂小结
第四部分
PART 04
your content is entered here, or by copying your text, select paste in this box and choose to retain only text. your content is typed here
利用三角函数测高
测倾器的认识及使用
测量底部可以到达的物体的高度(一次测量仰角)
测量底部不可以到达的物体的高度(两次测量仰角)
利用解三角形的知识,求出物体的高度
第一章 直角三角形的边角关系 1.6
利用三角
函数测高
北师大版九年级下册数学课件
