北师版九下数学-第一章-直角三角形的边角关系-小结与复习(共35张PPT)
文档属性
| 名称 | 北师版九下数学-第一章-直角三角形的边角关系-小结与复习(共35张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 2.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-01-27 10:33:33 | ||
图片预览









文档简介
(共35张PPT)
第一章 直角三角形的边角关系
小结与复习
北师大版九年级下册数学课件
目录
目录
CONTENTS
CONTENTS
1-新知导入
2-探究新知
3-巩固练习
4-课堂小结
新知导入
第一部分
PART 01
your content is entered here, or by copying your text, select paste in this box and choose to retain only text. your content is typed here
一、锐角三角函数
1. 如图所示,在 Rt△ABC 中,∠C = 90°,
a,b,c 分别是 ∠A,∠B,∠C 的对边.
(1) ∠A的正弦:sinA= = ;
(2)∠A的余弦:cosA= = ;
(3)∠A的正切:tanA= = .
2. 梯子的倾斜程度与 tanA、sinA 和cosA 的关系:
tanA 的值越大,梯子越陡;
sinA 的值越大,梯子越陡;
cosA 的值越小,梯子越陡.
3. 锐角三角函数的增减性:
当角度在 0°~90° 之间变化时,正弦值和正切值随着角度的增大(或减小)而 _______ ;
余弦值随着角度的增大(或减小)而 _______ .
增大(或减小)
减小(或增大)
探究新知
第二部分
PART 02
your content is entered here, or by copying your text, select paste in this box and choose to retain only text. your content is typed here
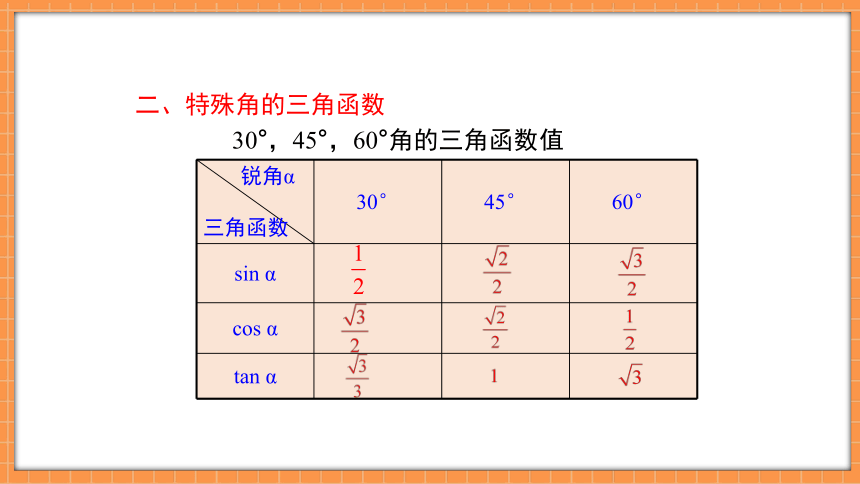
30°,45°,60°角的三角函数值
锐角α 三角函数 30° 45° 60°
sin α
cos α
tan α
二、特殊角的三角函数
1. 解直角三角形的依据
(1) 在 Rt△ABC 中,∠C = 90°,a,b,c 分别是 ∠A,∠B,∠C 的对边.
三边关系: ;
三角关系: ;
边角关系:sinA=cosB= ,cosA=sinB= ,
tanA= ,tanB= .
a2+b2=c2
∠A=90°-∠B
三、解直角三角形
(2) 直角三角形可解的条件和解法
条件:解直角三角形时知道其中的 2 个元素(至少有一个是边),就可以求出其余的 3 个未知元素.
解法:① 一边一锐角,先由两锐角互余关系求出另一锐角;知斜边,再用正弦(或余弦)求另两边;知直角边用正切求另一直角边,再用正弦或勾股定理求斜边;② 知两边:先用勾股定理求另一边,再用边角关系求锐角;③ 斜三角形问题可通过添加适当的辅助线转化为解直角三角形问题.
1. 利用计算器求三角函数值.
第二步:输入角度值,
屏幕显示结果.
(有的计算器是先输入角度再按函数名称键)
第一步:按计算器 、 、 键,
sin
tan
cos
四、锐角三角函数的计算
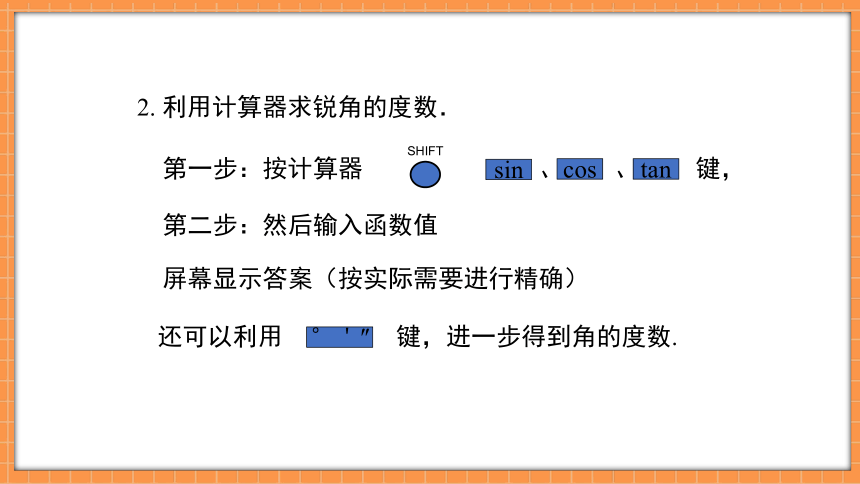
2. 利用计算器求锐角的度数.
还可以利用 键,进一步得到角的度数.
第二步:然后输入函数值
屏幕显示答案(按实际需要进行精确)
°'″
第一步:按计算器 、 、 键,
sin
cos
tan
SHIFT
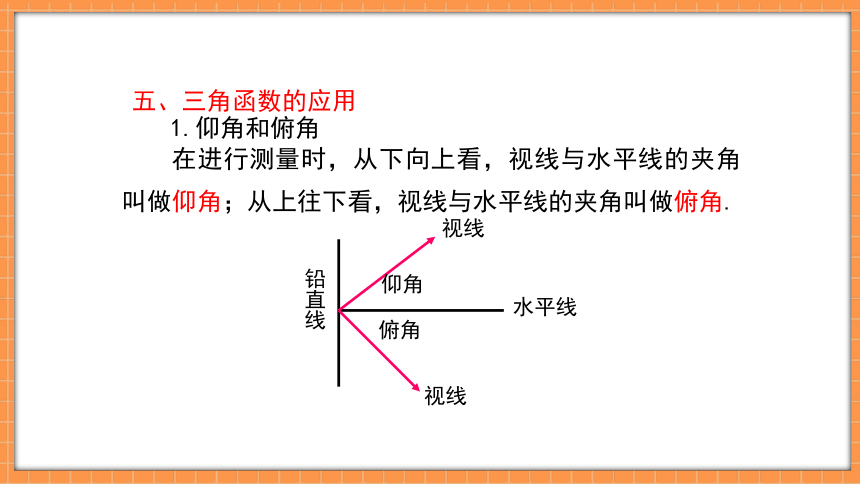
1.仰角和俯角
铅直线
水平线
视线
视线
仰角
俯角
在进行测量时,从下向上看,视线与水平线的夹角叫做仰角;从上往下看,视线与水平线的夹角叫做俯角.
五、三角函数的应用
以正南或正北方向为准,正南或正北方向线与目标方向线构成的小于 90° 的角,叫做方向角.如图所示:
30°
45°
B
O
A
东
西
北
南
2.方向角
45°
45°
西南
O
东北
东
西
北
南
西北
东南
α
l
h
h : l
(1)坡角
坡面与水平面的夹角叫做坡角,记作 α .
(2)坡度(或坡比)
坡度通常写成 1∶m 的形式,如 1∶6.
如图所示,坡面的铅垂高度(h)和水平长度(l)
的比叫做坡面的坡度(或坡比),即 —.
h
l
(3)坡度与坡角的关系
坡度等于坡角的正切值
坡面
水平面
3.坡角
利用解直角三角形的知识解决实际问题的一般过程是:
(1)将实际问题抽象为数学问题(画出平面图形,转化为解直角三角形的问题);
(2)根据条件的特点,适当选用锐角三角函数等去解直角三角形;
(3)得到数学问题的答案;
(4)得到实际问题的答案.
(2) 量出测点 A 到物体底部N的水平距离 AN = l;
A
C
M
N
(1) 在测点 A 安置测倾器,测得M的仰角∠MCE = α;
E
(3) 量出测倾器的高度 AC = a,
可求出 MN 的高度.
MN=ME+EN=l·tanα+a
α
1. 测量底部可以到达的物体的高度步骤:
六、利用三角函数测高
2.测量东方明珠的高度的步骤是怎么样的呢?
A
C
B
D
M
N
E
α
β
(1) 在测点 A 处安置测倾器,测得此时 M 的仰角
∠MCE = α;
(2) 在测点 A 与物体之间的 B 处安置测倾器,测得此 时 M 的仰角∠MDE = β;
(3) 量出测倾器的高度 AC = BD = a,以及测点 A,B 之间的距离 AB = b.根据测量数据,可求出物体 MN 的高度.
考点一 求三角函数的值
例1 在 △ABC 中,∠C = 90°,sinA= ,
则 tanB = ( )
A. B. C. D.
【解析】 根据 sinA = ,可设三角形的两边长分别为 4k,5k,则第三边长为3k,所以 tanB =
B
针对训练
1. 如图,在网格中,小正方形的边长均为 1,点 A,B,C 都在格点上,则 ∠ABC 的正弦值是________.
2. 用计算器求下列各式的值:
(1)cos63°17′ ≈ ______;
(2)tan27.35° ≈ ______;
(3)sin39°57′6″ ≈ ______.
0.45
0.52
0.64
3. 已知 sinα = 0.2,cosβ = 0.8,则 α+β =________(精确到1′).
48°24′
考点二 特殊角的三角函数值
【解析】本题考查数的0次幂、分母有理化和特殊角的三角函数值.
解:原式=
例2 计算
(1) tan30°+cos45°+tan60°
(2) tan30°· tan60°+ cos230°
4. 计算:
针对训练
解:原式
解:原式
考点三 解直角三角形
例3 如图,在 △ABC 中,∠C = 90°,点 D 在 BC 上,BD = 4,AD = BC,cos∠ADC = ,
求:(1) DC 的长;(2) sinB 的值.
【分析】题中给出了两个直角三角形,DC 和 sinB 可分别在 Rt△ACD 和 Rt△ABC 中求得,由 AD = BC,图中 CD=BC-BD,由此可列方程求出 CD.
A
B
C
D
解: (1) 设 CD = x,在 Rt△ACD 中,cos∠ADC= ,
又 BC-CD = BD,
解得 x = 6,
∴CD = 6.
A
B
C
D
(2) BC =BD+CD = 4+6 = 10 = AD
在 Rt△ACD 中
在 Rt△ABC 中
A
B
C
D
巩固练习
第三部分
PART 03
your content is entered here, or by copying your text, select paste in this box and choose to retain only text. your content is typed here
5. 如图,在 Rt△ABC 中,∠C = 90°,AC = .点D 为 BC 边上一点,且 BD = 2AD,∠ADC = 60°.求 △ABC 的周长(结果保留根号).
针对训练
解:在 Rt△ADC 中,
∴BD=2AD=4.
∴BC = BD+DC=5.
在 Rt△ABC 中,
∴△ABC 的周长=AB+BC+AC
考点四 三角函数的应用
例4 如图,在一次数学课外实践活动中,要求测教学楼 AB 的高度.小刚在 D 处用高 1.5 m 的测角仪 CD,测得教学楼顶端 A 的仰角为30°,然后向教学楼前进 40 m 到达 EF,又测得教学楼顶端 A 的仰角为 60°.求这幢教学楼 AB 的高度.
【分析】 设 CF 与 AB 交于点 G,在 Rt△AFG 中,用 AG 表示出 FG,在Rt△ACG 中,用 AG 表示出 CG,然后根据 CG-FG = 40,可求 AG.
G
解:设 CF 与 AB 交于点 G,在 Rt△AFG 中,
tan∠AFG = ,∴FG =
在 Rt△ACG 中,tan∠ACG = ,
又 CG-FG=40,
∴AG= ,∴AB =
答:这幢教学楼 AB 的高度为
∴
G
课堂小结
第四部分
PART 04
your content is entered here, or by copying your text, select paste in this box and choose to retain only text. your content is typed here
6.如图,某人站在楼顶观测对面的笔直的旗杆 AB ,已知观测点 C 到旗杆的距离(即 CE 的长)为 8 米,测得旗杆顶的仰角 ∠ECA 为 30°,旗杆底部的俯角 ∠ECB 为 45 °,则旗杆 AB 的高度是多少米
C
A
B
D
E
解:如图在 Rt△ACE 和 Rt△BCE 中
∠ACE = 30°,EC = 8米,
∴tan∠ACE = ,tan∠ECB =
即:AE = 8tan30°= (米) ,
EB = 8tan45° = 8(米).
∴AB = AE+EB = (8+ )米.
针对训练
锐角三角
函数
特殊角的三
角函数
解直角三
角形
简单实际
问题
c
a
b
A
B
C
第一章 直角三角形的边角关系
小结与复习
北师大版九年级下册数学课件
第一章 直角三角形的边角关系
小结与复习
北师大版九年级下册数学课件
目录
目录
CONTENTS
CONTENTS
1-新知导入
2-探究新知
3-巩固练习
4-课堂小结
新知导入
第一部分
PART 01
your content is entered here, or by copying your text, select paste in this box and choose to retain only text. your content is typed here
一、锐角三角函数
1. 如图所示,在 Rt△ABC 中,∠C = 90°,
a,b,c 分别是 ∠A,∠B,∠C 的对边.
(1) ∠A的正弦:sinA= = ;
(2)∠A的余弦:cosA= = ;
(3)∠A的正切:tanA= = .
2. 梯子的倾斜程度与 tanA、sinA 和cosA 的关系:
tanA 的值越大,梯子越陡;
sinA 的值越大,梯子越陡;
cosA 的值越小,梯子越陡.
3. 锐角三角函数的增减性:
当角度在 0°~90° 之间变化时,正弦值和正切值随着角度的增大(或减小)而 _______ ;
余弦值随着角度的增大(或减小)而 _______ .
增大(或减小)
减小(或增大)
探究新知
第二部分
PART 02
your content is entered here, or by copying your text, select paste in this box and choose to retain only text. your content is typed here
30°,45°,60°角的三角函数值
锐角α 三角函数 30° 45° 60°
sin α
cos α
tan α
二、特殊角的三角函数
1. 解直角三角形的依据
(1) 在 Rt△ABC 中,∠C = 90°,a,b,c 分别是 ∠A,∠B,∠C 的对边.
三边关系: ;
三角关系: ;
边角关系:sinA=cosB= ,cosA=sinB= ,
tanA= ,tanB= .
a2+b2=c2
∠A=90°-∠B
三、解直角三角形
(2) 直角三角形可解的条件和解法
条件:解直角三角形时知道其中的 2 个元素(至少有一个是边),就可以求出其余的 3 个未知元素.
解法:① 一边一锐角,先由两锐角互余关系求出另一锐角;知斜边,再用正弦(或余弦)求另两边;知直角边用正切求另一直角边,再用正弦或勾股定理求斜边;② 知两边:先用勾股定理求另一边,再用边角关系求锐角;③ 斜三角形问题可通过添加适当的辅助线转化为解直角三角形问题.
1. 利用计算器求三角函数值.
第二步:输入角度值,
屏幕显示结果.
(有的计算器是先输入角度再按函数名称键)
第一步:按计算器 、 、 键,
sin
tan
cos
四、锐角三角函数的计算
2. 利用计算器求锐角的度数.
还可以利用 键,进一步得到角的度数.
第二步:然后输入函数值
屏幕显示答案(按实际需要进行精确)
°'″
第一步:按计算器 、 、 键,
sin
cos
tan
SHIFT
1.仰角和俯角
铅直线
水平线
视线
视线
仰角
俯角
在进行测量时,从下向上看,视线与水平线的夹角叫做仰角;从上往下看,视线与水平线的夹角叫做俯角.
五、三角函数的应用
以正南或正北方向为准,正南或正北方向线与目标方向线构成的小于 90° 的角,叫做方向角.如图所示:
30°
45°
B
O
A
东
西
北
南
2.方向角
45°
45°
西南
O
东北
东
西
北
南
西北
东南
α
l
h
h : l
(1)坡角
坡面与水平面的夹角叫做坡角,记作 α .
(2)坡度(或坡比)
坡度通常写成 1∶m 的形式,如 1∶6.
如图所示,坡面的铅垂高度(h)和水平长度(l)
的比叫做坡面的坡度(或坡比),即 —.
h
l
(3)坡度与坡角的关系
坡度等于坡角的正切值
坡面
水平面
3.坡角
利用解直角三角形的知识解决实际问题的一般过程是:
(1)将实际问题抽象为数学问题(画出平面图形,转化为解直角三角形的问题);
(2)根据条件的特点,适当选用锐角三角函数等去解直角三角形;
(3)得到数学问题的答案;
(4)得到实际问题的答案.
(2) 量出测点 A 到物体底部N的水平距离 AN = l;
A
C
M
N
(1) 在测点 A 安置测倾器,测得M的仰角∠MCE = α;
E
(3) 量出测倾器的高度 AC = a,
可求出 MN 的高度.
MN=ME+EN=l·tanα+a
α
1. 测量底部可以到达的物体的高度步骤:
六、利用三角函数测高
2.测量东方明珠的高度的步骤是怎么样的呢?
A
C
B
D
M
N
E
α
β
(1) 在测点 A 处安置测倾器,测得此时 M 的仰角
∠MCE = α;
(2) 在测点 A 与物体之间的 B 处安置测倾器,测得此 时 M 的仰角∠MDE = β;
(3) 量出测倾器的高度 AC = BD = a,以及测点 A,B 之间的距离 AB = b.根据测量数据,可求出物体 MN 的高度.
考点一 求三角函数的值
例1 在 △ABC 中,∠C = 90°,sinA= ,
则 tanB = ( )
A. B. C. D.
【解析】 根据 sinA = ,可设三角形的两边长分别为 4k,5k,则第三边长为3k,所以 tanB =
B
针对训练
1. 如图,在网格中,小正方形的边长均为 1,点 A,B,C 都在格点上,则 ∠ABC 的正弦值是________.
2. 用计算器求下列各式的值:
(1)cos63°17′ ≈ ______;
(2)tan27.35° ≈ ______;
(3)sin39°57′6″ ≈ ______.
0.45
0.52
0.64
3. 已知 sinα = 0.2,cosβ = 0.8,则 α+β =________(精确到1′).
48°24′
考点二 特殊角的三角函数值
【解析】本题考查数的0次幂、分母有理化和特殊角的三角函数值.
解:原式=
例2 计算
(1) tan30°+cos45°+tan60°
(2) tan30°· tan60°+ cos230°
4. 计算:
针对训练
解:原式
解:原式
考点三 解直角三角形
例3 如图,在 △ABC 中,∠C = 90°,点 D 在 BC 上,BD = 4,AD = BC,cos∠ADC = ,
求:(1) DC 的长;(2) sinB 的值.
【分析】题中给出了两个直角三角形,DC 和 sinB 可分别在 Rt△ACD 和 Rt△ABC 中求得,由 AD = BC,图中 CD=BC-BD,由此可列方程求出 CD.
A
B
C
D
解: (1) 设 CD = x,在 Rt△ACD 中,cos∠ADC= ,
又 BC-CD = BD,
解得 x = 6,
∴CD = 6.
A
B
C
D
(2) BC =BD+CD = 4+6 = 10 = AD
在 Rt△ACD 中
在 Rt△ABC 中
A
B
C
D
巩固练习
第三部分
PART 03
your content is entered here, or by copying your text, select paste in this box and choose to retain only text. your content is typed here
5. 如图,在 Rt△ABC 中,∠C = 90°,AC = .点D 为 BC 边上一点,且 BD = 2AD,∠ADC = 60°.求 △ABC 的周长(结果保留根号).
针对训练
解:在 Rt△ADC 中,
∴BD=2AD=4.
∴BC = BD+DC=5.
在 Rt△ABC 中,
∴△ABC 的周长=AB+BC+AC
考点四 三角函数的应用
例4 如图,在一次数学课外实践活动中,要求测教学楼 AB 的高度.小刚在 D 处用高 1.5 m 的测角仪 CD,测得教学楼顶端 A 的仰角为30°,然后向教学楼前进 40 m 到达 EF,又测得教学楼顶端 A 的仰角为 60°.求这幢教学楼 AB 的高度.
【分析】 设 CF 与 AB 交于点 G,在 Rt△AFG 中,用 AG 表示出 FG,在Rt△ACG 中,用 AG 表示出 CG,然后根据 CG-FG = 40,可求 AG.
G
解:设 CF 与 AB 交于点 G,在 Rt△AFG 中,
tan∠AFG = ,∴FG =
在 Rt△ACG 中,tan∠ACG = ,
又 CG-FG=40,
∴AG= ,∴AB =
答:这幢教学楼 AB 的高度为
∴
G
课堂小结
第四部分
PART 04
your content is entered here, or by copying your text, select paste in this box and choose to retain only text. your content is typed here
6.如图,某人站在楼顶观测对面的笔直的旗杆 AB ,已知观测点 C 到旗杆的距离(即 CE 的长)为 8 米,测得旗杆顶的仰角 ∠ECA 为 30°,旗杆底部的俯角 ∠ECB 为 45 °,则旗杆 AB 的高度是多少米
C
A
B
D
E
解:如图在 Rt△ACE 和 Rt△BCE 中
∠ACE = 30°,EC = 8米,
∴tan∠ACE = ,tan∠ECB =
即:AE = 8tan30°= (米) ,
EB = 8tan45° = 8(米).
∴AB = AE+EB = (8+ )米.
针对训练
锐角三角
函数
特殊角的三
角函数
解直角三
角形
简单实际
问题
c
a
b
A
B
C
第一章 直角三角形的边角关系
小结与复习
北师大版九年级下册数学课件
