2.5.1 矩形的性质 学案

中小学教育资源及组卷应用平台
学习任务单
课程基本信息
学科 数学 年级 九年级 学期 秋季
课题 2.5.1矩形的性质
教科书 书 名：义务教育教科书数学八年级下册 出版社：湖南教育出版社
学生信息
姓名 学校 班级 学号
学习目标
1.掌握矩形的概念和性质，理解矩形与平行四边形的区别与联系． 2.会初步运用矩形的概念和性质来解决有关问题．
课前学习任务
复习引入 当独木桥前后运动时，四边形ABCD是什么形状？ 当独木桥最后停下时，四边形ABCD有什么特殊的变化？当独木桥静止时，四边形ABCD是什么图形？
课上学习任务
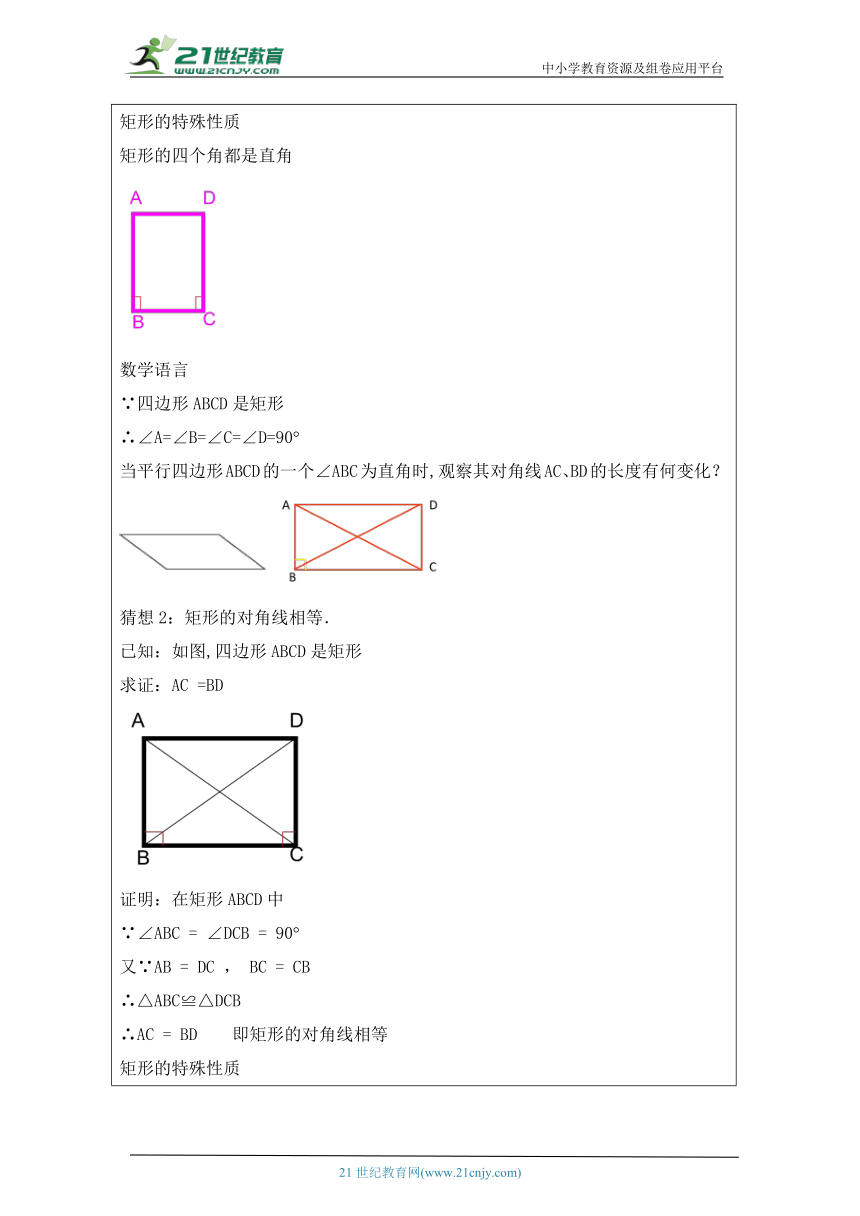
【学习任务一】 观察 图中的长方形是平行四边形吗？它有什么特点呢？ 如图，这是一个活动框架，改变这个平行四边形的形状，你会发现什么 矩形的定义： 有一个角是直角的平行四边形叫做矩形，也称为长方形。 矩形是特殊的平行四边形。 想一想： 你能举出在人们的日常生活和生产实践中，有哪些东西是矩形的？ 矩形的一般性质： 1.矩形的两组对边分别平行 2.矩形的两组对边分别相等 【学习任务二】 动脑筋 矩形是一个特殊的平行四边形，除了具有平行四边形的所有性质外，还有哪些特殊性质呢？ 当平行四边形ABCD的一个∠ABC为直角时,观察其它角 猜想1：矩形的四个角都是直角． 已知：如图，四边形ABCD是矩形 求证：∠A=∠B=∠C=∠D=90° 证明： ∵四边形ABCD是矩形。 ∴ ∠A=90° 又矩形ABCD是平行四边形 ∴ ∠A=∠C ∠B = ∠D ∠A +∠B =180° ∴ ∠A=∠B=∠C=∠D=90° 即矩形的四个角都是直角 矩形的特殊性质 矩形的四个角都是直角 数学语言 ∵四边形ABCD是矩形 ∴∠A=∠B=∠C=∠D=90° 当平行四边形ABCD的一个∠ABC为直角时,观察其对角线AC、BD的长度有何变化？ 猜想2：矩形的对角线相等． 已知：如图,四边形ABCD是矩形 求证：AC =BD 证明：在矩形ABCD中 ∵∠ABC = ∠DCB = 90° 又∵AB = DC ， BC = CB ∴△ABC≌△DCB ∴AC = BD 即矩形的对角线相等 矩形的特殊性质 矩形的对角线相等 数学语言 ∵四边形ABCD是矩形 ∴AC = BD 矩形特殊的性质 从角上看：矩形的四个角都是直角． 从对角线上看：矩形的两条对角线相等，且互相平分 【学习任务三】 例1 如图，矩形ABCD的两条对角线AC、BD相交于点O, AC= 4cm ，∠AOB=60°。求BC的长。 做一做 画出一个矩形ABCD，把它减下来，怎样折叠能使矩形在折痕两旁的部分互相重合？满足这个要求的折叠方法有几种？由此猜测：矩形是轴对称图形吗？如果是，它有几条对称轴？你的猜测正确吗？ 猜测：矩形是轴对称图形，有两条对称轴。 矩形是轴对称图形,过每一组对边中点的直线都是矩形的对称轴. 试着去证明猜测吧！ 【学习任务四】课堂练习 必做题： 1.如图，在矩形ABCD中，若AC=2AB，则∠AOB的大小是( ) A.30°B.45°C.60°D.90° 选做题： 2.如图，在矩形ABCD中，对角线AC，BD相交于点O，点E，F分别是AO，AD的中点，若AB=6 cm，BC=8 cm，则△AEF的周长=__________cm. . 【综合拓展类作业】 3、四个学生正在做投圈游戏，他们分别站在一个矩形的四个顶点处，目标物放在对角线的交点处，这样的队形对每个人公平吗？为什么？ 【知识技能类作业】 必做题： 1.如图，矩形ABCD的对角线AC，BD相交于点O，CE∥BD，DE∥AC.若AC=4，则四边形CODE的周长是( ) A.4 B.6 C.8 D.10 选做题： 2. 如图，矩形ABCD中，点E,F分别是AB,CD的中点，连接DE和BF，分别取DE,BF的中点M,N，连接AM,CN,MN，若AB=2 ，BC=2 ，则图中阴影部分的面积为__________. 【综合拓展类作业】 3.如图，四边形ABCD是矩形，试利用矩形的性质说明：在直角三角形ABC斜边AC上的中线BD等于斜边的一半.
21世纪教育网(www.21cnjy.com)