6.1.2 向量的加法 课件(共20张PPT) 2024-2025学年人教B版高中数学必修第二册
文档属性
| 名称 | 6.1.2 向量的加法 课件(共20张PPT) 2024-2025学年人教B版高中数学必修第二册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 1016.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教B版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-01-25 19:11:11 | ||
图片预览








文档简介
(共20张PPT)
第六章
6.1.2 向量的加法
1.理解并掌握向量加法的概念,了解向量加法的几何意义及其运算律.(数学抽象)
2.掌握向量加法运算法则,能熟练地进行加法运算.(数
学抽象、直观想象)
3.理解数的加法与向量的加法的联系与区别.(逻辑推理)
4.会用向量加法的三角形法则和平行四边形法则求两个向量的和.(直观想象)
“马走日”是中国象棋中“马”的走法,是指“马”走一步时只能是从一个“日”字形的棋格一个顶点跳到与之对顶的顶点.我们可以用从出发点到目的点的有向线段来表示马走了“一步”.即“马”每走一步可以用一个向量来表示.
那么想要让“马”从棋盘上的一个点走到它所在位置左侧的相邻点,应该如何实现呢
知识点一 向量加法的定义
求__________的运算,叫作向量的加法.
两个向量和
知识点二 向量加法的运算法则
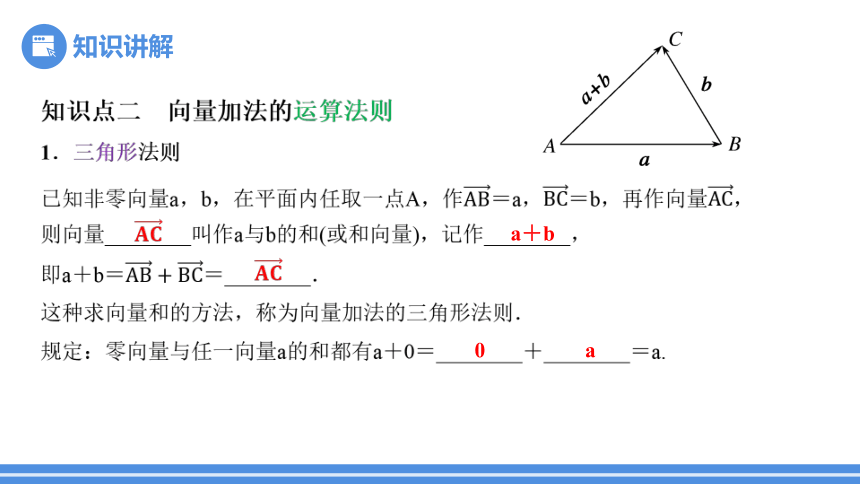
1.三角形法则
已知非零向量a,b,在平面内任取一点A,作=a,=b,再作向量,
则向量________叫作a与b的和(或和向量),记作________,
即a+b==________.
这种求向量和的方法,称为向量加法的三角形法则.
规定:零向量与任一向量a的和都有a+0=________+________=a.
a+b
0
a
2.平行四边形法则
如图,以同一点O为起点的两个已知向量a,b为邻边作 OACB,
则以O为起点的__________就是a与b的和,
我们把这种作两个向量和的方法叫作向量加法的平行四边形法则.
对角线
知识点三 向量加法的运算律
1.交换律:a+b=________.
2.结合律:(a+b)+c=________+(________).
b+a
a
b+c
点拨:1.准确理解向量加法的三角形法则和平行四边形法则
(1)两个法则的使用条件不同:
三角形法则适用于任意两个非零向量求和,平行四边形法则只适用于两个不共线的向量求和.
(2)当两个向量不共线时,两个法则是一致的.
如图所示:=+(平行四边形法则),
又∵=,∴=+(三角形法则).
(3)在使用三角形法则时,应注意“首尾连接”;
在使用平行四边形法则时应注意范围的限制及和向量与两向量起点相同.
2.向量+与非零向量的模及方向的联系
(1)当向量与不共线时,向量的方向与都不相同,
且||<||+||,几何意义是三角形两边之和大于第三边.
(2)当向量与同向时,向量与(或)方向相同,且||=||+||.
(3)当向量与反向时,且||≤||时,
+与方向相同(与方向相反),且||=||-||.
题型1 已知向量作和向量(经典例题)
例1 如图,已知向量a,b,c,求作和向量a+b+c.
解析:(方法一)可先作a+c,再作(a+c)+b,即a+b+c.如图①,
首先在平面内任取一点O,作向量=a,
接着作向量=c,则得向量=a+c,
然后作向量=b,则向量=a+b+c为所求.
图①
(方法二)三个向量不共线,用平行四边形法则来作.如图②,
(1)在平面内任取一点O,作=a,=b;
(2)作平行四边形AOBC,则=a+b;
(3)再作向量=c;
(4)作平行四边形CODE,则=+c=a+b+c.即为所求.
图②
方法归纳
(1)应用三角形法则求向量和的基本步骤
①平移向量使之“首尾相接”,即第一个向量的终点与第二个向量的起点重合.
②以第一个向量的起点为起点,并以第二个向量的终点为终点的向量,
即为两个向量的和.
(2)应用平行四边形法则求向量和的基本步骤
①平移两个不共线的向量使之共起点.
②以这两个已知向量为邻边作平行四边形.
③平行四边形中,与两向量共起点的对角线表示的向量为两个向量的和.
题型2 向量的加法运算(教材P141例2)
例2 化简下列各式:
(1);
(2).
解析:(1)=()+==.
(2)=+()
==()+
===0.
点拨:先根据向量加法的交换律变为各向量首尾相连,然后利用向量的加法运算求解.
教材反思
向量运算中化简的两种方法
(1)代数法:借助向量加法的交换律和结合律,将向量转化为“首尾相接”,
向量的和即为第一个向量的起点指向最后一个向量终点的向量.
(2)几何法:通过作图,根据“三角形法则”或“平行四边形法则”化简.
1.在平行四边形ABCD中,下列结论中错误的是( )
A.=
B.=
C.=
D.=0
解析:因为=+≠+,C错误.
答案:C
2.向量 化简后等于 .
答案:
解析:
3.如图,已知向量a,b,c不共线,作向量a+b+c.
分析:本题是求向量的和问题,方法是使用三角形法则或平行四边形法则.
解析:(方法一) 如图(1),在平面内作=a,=b,
则=a+b;再作=c,则=a+b+c.
(方法二) 如图(2),在平面内作=a,=b,
以OA与OB为邻边作平行四边形OADB,
则=a+b;再作=c,
以OD与OC为邻边作平行四边形ODEC,
则=a+b+c.
向量的加法
向量加法的三角形法则
向量加法的平行四边形法则
多个向量相加
交换律
结合律
第六章
6.1.2 向量的加法
1.理解并掌握向量加法的概念,了解向量加法的几何意义及其运算律.(数学抽象)
2.掌握向量加法运算法则,能熟练地进行加法运算.(数
学抽象、直观想象)
3.理解数的加法与向量的加法的联系与区别.(逻辑推理)
4.会用向量加法的三角形法则和平行四边形法则求两个向量的和.(直观想象)
“马走日”是中国象棋中“马”的走法,是指“马”走一步时只能是从一个“日”字形的棋格一个顶点跳到与之对顶的顶点.我们可以用从出发点到目的点的有向线段来表示马走了“一步”.即“马”每走一步可以用一个向量来表示.
那么想要让“马”从棋盘上的一个点走到它所在位置左侧的相邻点,应该如何实现呢
知识点一 向量加法的定义
求__________的运算,叫作向量的加法.
两个向量和
知识点二 向量加法的运算法则
1.三角形法则
已知非零向量a,b,在平面内任取一点A,作=a,=b,再作向量,
则向量________叫作a与b的和(或和向量),记作________,
即a+b==________.
这种求向量和的方法,称为向量加法的三角形法则.
规定:零向量与任一向量a的和都有a+0=________+________=a.
a+b
0
a
2.平行四边形法则
如图,以同一点O为起点的两个已知向量a,b为邻边作 OACB,
则以O为起点的__________就是a与b的和,
我们把这种作两个向量和的方法叫作向量加法的平行四边形法则.
对角线
知识点三 向量加法的运算律
1.交换律:a+b=________.
2.结合律:(a+b)+c=________+(________).
b+a
a
b+c
点拨:1.准确理解向量加法的三角形法则和平行四边形法则
(1)两个法则的使用条件不同:
三角形法则适用于任意两个非零向量求和,平行四边形法则只适用于两个不共线的向量求和.
(2)当两个向量不共线时,两个法则是一致的.
如图所示:=+(平行四边形法则),
又∵=,∴=+(三角形法则).
(3)在使用三角形法则时,应注意“首尾连接”;
在使用平行四边形法则时应注意范围的限制及和向量与两向量起点相同.
2.向量+与非零向量的模及方向的联系
(1)当向量与不共线时,向量的方向与都不相同,
且||<||+||,几何意义是三角形两边之和大于第三边.
(2)当向量与同向时,向量与(或)方向相同,且||=||+||.
(3)当向量与反向时,且||≤||时,
+与方向相同(与方向相反),且||=||-||.
题型1 已知向量作和向量(经典例题)
例1 如图,已知向量a,b,c,求作和向量a+b+c.
解析:(方法一)可先作a+c,再作(a+c)+b,即a+b+c.如图①,
首先在平面内任取一点O,作向量=a,
接着作向量=c,则得向量=a+c,
然后作向量=b,则向量=a+b+c为所求.
图①
(方法二)三个向量不共线,用平行四边形法则来作.如图②,
(1)在平面内任取一点O,作=a,=b;
(2)作平行四边形AOBC,则=a+b;
(3)再作向量=c;
(4)作平行四边形CODE,则=+c=a+b+c.即为所求.
图②
方法归纳
(1)应用三角形法则求向量和的基本步骤
①平移向量使之“首尾相接”,即第一个向量的终点与第二个向量的起点重合.
②以第一个向量的起点为起点,并以第二个向量的终点为终点的向量,
即为两个向量的和.
(2)应用平行四边形法则求向量和的基本步骤
①平移两个不共线的向量使之共起点.
②以这两个已知向量为邻边作平行四边形.
③平行四边形中,与两向量共起点的对角线表示的向量为两个向量的和.
题型2 向量的加法运算(教材P141例2)
例2 化简下列各式:
(1);
(2).
解析:(1)=()+==.
(2)=+()
==()+
===0.
点拨:先根据向量加法的交换律变为各向量首尾相连,然后利用向量的加法运算求解.
教材反思
向量运算中化简的两种方法
(1)代数法:借助向量加法的交换律和结合律,将向量转化为“首尾相接”,
向量的和即为第一个向量的起点指向最后一个向量终点的向量.
(2)几何法:通过作图,根据“三角形法则”或“平行四边形法则”化简.
1.在平行四边形ABCD中,下列结论中错误的是( )
A.=
B.=
C.=
D.=0
解析:因为=+≠+,C错误.
答案:C
2.向量 化简后等于 .
答案:
解析:
3.如图,已知向量a,b,c不共线,作向量a+b+c.
分析:本题是求向量的和问题,方法是使用三角形法则或平行四边形法则.
解析:(方法一) 如图(1),在平面内作=a,=b,
则=a+b;再作=c,则=a+b+c.
(方法二) 如图(2),在平面内作=a,=b,
以OA与OB为邻边作平行四边形OADB,
则=a+b;再作=c,
以OD与OC为邻边作平行四边形ODEC,
则=a+b+c.
向量的加法
向量加法的三角形法则
向量加法的平行四边形法则
多个向量相加
交换律
结合律
