11.3.3 平面与平面平行 课件(共21张PPT)2024-2025学年人教B版高中数学必修第四册
文档属性
| 名称 | 11.3.3 平面与平面平行 课件(共21张PPT)2024-2025学年人教B版高中数学必修第四册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教B版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-01-25 00:00:00 | ||
图片预览





文档简介
(共21张PPT)
11.3.3 平面与平面平行
1.理解平面与平面平行的判定定理与性质定理. (重点)
2.能够运用判定定理和性质定理证明简单的平行问题.(难点)
情景导入
生活中有好多平面与平面平行的例子,你能结合下图说一说吗?
1.天花板与地面
2.书架的隔板
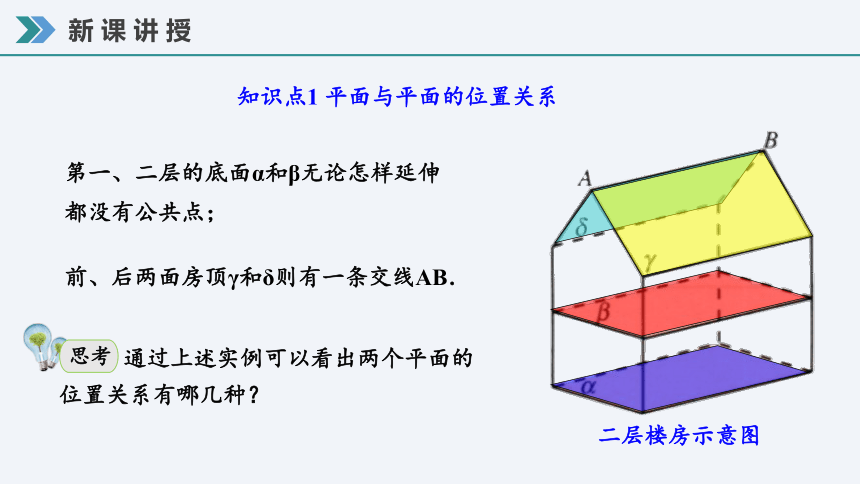
二层楼房示意图
第一、二层的底面α和β无论怎样延伸都没有公共点;
前、后两面房顶γ和δ则有一条交线AB.
知识点1 平面与平面的位置关系
通过上述实例可以看出两个平面的位置关系有哪几种?
思考
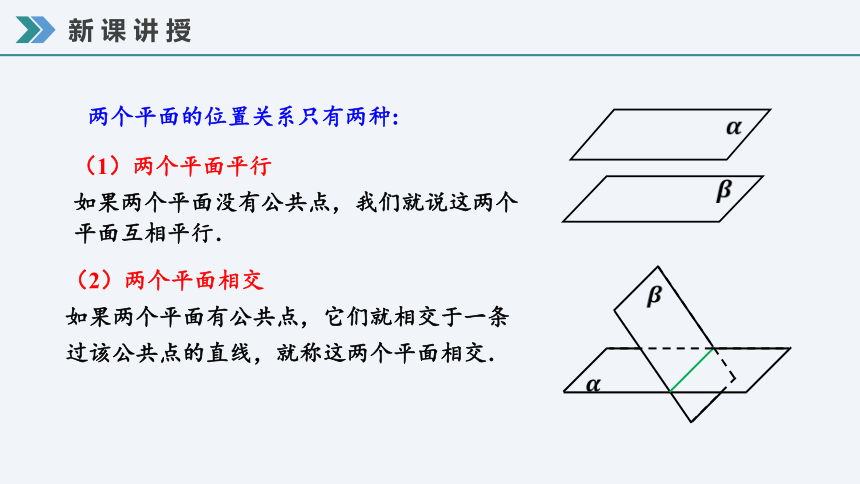
(1)两个平面平行
如果两个平面没有公共点,我们就说这两个平面互相平行.
(2)两个平面相交
如果两个平面有公共点,它们就相交于一条过该公共点的直线,就称这两个平面相交.
两个平面的位置关系只有两种:
知识点2 平面与平面平行的判定
可以利用定义,即用平面与平面交点的个数进行判定.
但是我们知道这种方法是很困难的.
追问:如果用线面平行来推的话,最少需要几条直线呢?什么样的直线呢?
如何判定两个平面平行呢?
思考1
l′
m′
α
β
m
l
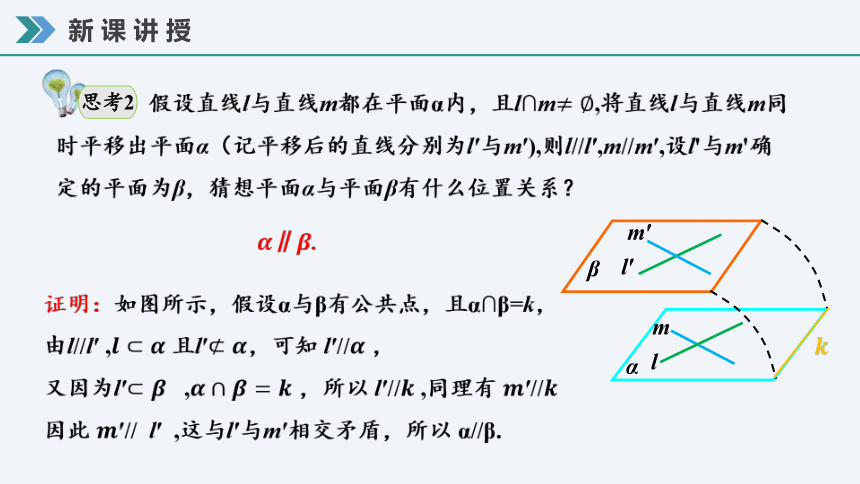
∥.
证明:如图所示,假设α与β有公共点,且α∩β=k,
由l//l′ , 且l′,可知 l′// ,
又因为l′ , ,所以 l′// ,同理有 ′//
因此 ′// l′ ,这与l′与m′相交矛盾,所以 α//β.
假设直线l与直线m都在平面α内,且l∩m,将直线l与直线m同时平移出平面α(记平移后的直线分别为l′与m′),则l//l′,m//m′,设l'与m'确定的平面为β,猜想平面α与平面β有什么位置关系?
思考2
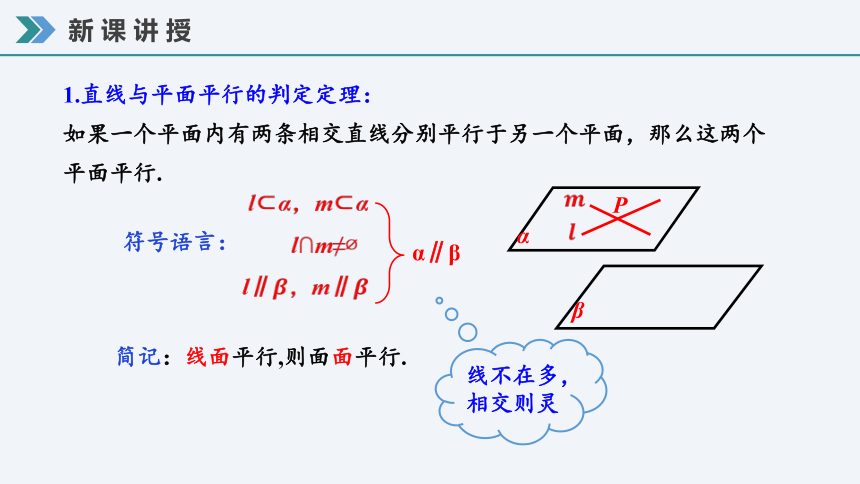
1.直线与平面平行的判定定理:
如果一个平面内有两条相交直线分别平行于另一个平面,那么这两个平面平行.
α
β
P
符号语言:
简记:线面平行,则面面平行.
线不在多,相交则灵
l α,m α
l∩m≠
l∥,m∥
α∥β
α
β
l′
m′
可用“l′ β,m′ β,l与m 相交,l∥l′,m∥m′”代替.
l
m
在平面与平面平行的判定定理中,“∥,∥”,可用什么条件替代?由此可得什么推论?
思考3
2.平面与平面平行判定定理的推论:
如果一个平面内有两条相交直线分别平行于另一个平面内的两条直线,则这两个平面平行.
α
β
l′
m′
l
m
l α,m α,l∩m≠ ,
l′ β,m′ β,
l∥l′,m∥m′,
α∥β.
符号语言:
简记:线线平行,则面面平行.
例1 如图所示,己知三棱锥P-ABC中,D,E,F分别是PA,PB,PC的中点,求证:面DEF//面ABC.
证明:在△PAB中,因为D,E分别是PA,PB的中点,所以DE//AB.
又知DE 平面ABC,AB 平面ABC,因此DE/∥平面ABC.
同理,EF//平面ABC.
又因为DE∩EF=E,所以由面面平行的判定定理可得
面DEF//面ABC.
例题讲解
第一步:在一个平面内找出两条相交直线;
第三步:利用判定定理得出结论.
证明平面与平面平行的一般步骤为:
第二步:证明两条相交直线分别平行于另一个平面;
方法总结
a
如果两个平面平行,那么一个平面内的直线与另一个平面平行.
如果两个平面平行,那么一个平面内的直线与另一个平面有什么位置关系?
知识点3 平面与平面平行的性质
,,则
符号语言:
思考1
如果两个平面平行,那么两个平面内的直线不是异面关系,就是平行关系.
如果两个平面平行,两个平面内的直线有什么位置关系?
思考2
当第三个平面和两个平行平面都相交时,两条交线有什么关系?为什么?
两条交线平行.
证明:如图,因为 ,所以与没有公共点
又因为 ,所以 .
注意到 且 ,
所以与共面且没有公共点,即.
思考1
平面与平面平行的性质定理:
如果两个平行平面同时与第三个平面相交,那么它们的交线平行.
符号语言:
简记:面面平行,则线线平行.
例2 如图所示,已知都是平面,且,两条直线分别于平面相交于A,B,C和点D,E,F,求证:.
证明:如图所示,连接DC,设DC与平面β相交于点G,
则平面ACD与平面α,β分别相交于直线AD,BG,
平面DCF与平面β,γ分别相交于直线GE,CF.
因为α//β. ∴BG//AD,因此△CBG∽△CAD
同理可得
因此,
例题讲解
证明:如图所示,连接B1D1.
∵P、N分别是D1C1、B1C1的中点,
∴PN∥B1D1.∵DD1∥BB1,DD1=BB1,
∴四边形B1BDD1为平行四边形,
∴B1D1∥BD,PN∥BD.
∵PN 平面A1BD,BD 平面A1BD,∴PN∥平面A1BD
在正方体ABCD-A1B1C1D1中,M、N、P分别是C1C、B1C1、C1D1的中点,求证:平面MNP∥平面A1BD.
同理可证MN∥平面A1BD,
又PN∩MN=N,PN 平面MNP,MN 平面MNP
∴平面PMN∥平面A1BD.
练一练
1.平面α//平面β的一个充分条件是( )
A.存在一条直线a,a//α,a//β
B.存在一条直线a,a α,a//β
C.存在两条平行直线a、b,a α,b β,a//β,b//α
D.存在两条异面直线a、b,a α,b β,a//β,b//α
D
2.如图所示,在直角梯形ABCP中,BC∥AP,AB⊥BC,CD⊥AP,AD=DC=PD. E,F,G分别为线段PC,PD,BC的中点,现将△PDC折起,使点P平面ABCD.
求证:平面PAB∥平面EFG.
证明:因为PE=EC,PF=FD,所以EF∥CD,
又因为CD∥AB,
所以EF∥AB,又EF平面PAB,AB平面PAB,
所以EF∥平面PAB,同理可证EG∥平面PAB.
又因为EF∩EG=E,
所以平面PAB∥平面EFG.
11.3.3 平面与平面平行
1.理解平面与平面平行的判定定理与性质定理. (重点)
2.能够运用判定定理和性质定理证明简单的平行问题.(难点)
情景导入
生活中有好多平面与平面平行的例子,你能结合下图说一说吗?
1.天花板与地面
2.书架的隔板
二层楼房示意图
第一、二层的底面α和β无论怎样延伸都没有公共点;
前、后两面房顶γ和δ则有一条交线AB.
知识点1 平面与平面的位置关系
通过上述实例可以看出两个平面的位置关系有哪几种?
思考
(1)两个平面平行
如果两个平面没有公共点,我们就说这两个平面互相平行.
(2)两个平面相交
如果两个平面有公共点,它们就相交于一条过该公共点的直线,就称这两个平面相交.
两个平面的位置关系只有两种:
知识点2 平面与平面平行的判定
可以利用定义,即用平面与平面交点的个数进行判定.
但是我们知道这种方法是很困难的.
追问:如果用线面平行来推的话,最少需要几条直线呢?什么样的直线呢?
如何判定两个平面平行呢?
思考1
l′
m′
α
β
m
l
∥.
证明:如图所示,假设α与β有公共点,且α∩β=k,
由l//l′ , 且l′,可知 l′// ,
又因为l′ , ,所以 l′// ,同理有 ′//
因此 ′// l′ ,这与l′与m′相交矛盾,所以 α//β.
假设直线l与直线m都在平面α内,且l∩m,将直线l与直线m同时平移出平面α(记平移后的直线分别为l′与m′),则l//l′,m//m′,设l'与m'确定的平面为β,猜想平面α与平面β有什么位置关系?
思考2
1.直线与平面平行的判定定理:
如果一个平面内有两条相交直线分别平行于另一个平面,那么这两个平面平行.
α
β
P
符号语言:
简记:线面平行,则面面平行.
线不在多,相交则灵
l α,m α
l∩m≠
l∥,m∥
α∥β
α
β
l′
m′
可用“l′ β,m′ β,l与m 相交,l∥l′,m∥m′”代替.
l
m
在平面与平面平行的判定定理中,“∥,∥”,可用什么条件替代?由此可得什么推论?
思考3
2.平面与平面平行判定定理的推论:
如果一个平面内有两条相交直线分别平行于另一个平面内的两条直线,则这两个平面平行.
α
β
l′
m′
l
m
l α,m α,l∩m≠ ,
l′ β,m′ β,
l∥l′,m∥m′,
α∥β.
符号语言:
简记:线线平行,则面面平行.
例1 如图所示,己知三棱锥P-ABC中,D,E,F分别是PA,PB,PC的中点,求证:面DEF//面ABC.
证明:在△PAB中,因为D,E分别是PA,PB的中点,所以DE//AB.
又知DE 平面ABC,AB 平面ABC,因此DE/∥平面ABC.
同理,EF//平面ABC.
又因为DE∩EF=E,所以由面面平行的判定定理可得
面DEF//面ABC.
例题讲解
第一步:在一个平面内找出两条相交直线;
第三步:利用判定定理得出结论.
证明平面与平面平行的一般步骤为:
第二步:证明两条相交直线分别平行于另一个平面;
方法总结
a
如果两个平面平行,那么一个平面内的直线与另一个平面平行.
如果两个平面平行,那么一个平面内的直线与另一个平面有什么位置关系?
知识点3 平面与平面平行的性质
,,则
符号语言:
思考1
如果两个平面平行,那么两个平面内的直线不是异面关系,就是平行关系.
如果两个平面平行,两个平面内的直线有什么位置关系?
思考2
当第三个平面和两个平行平面都相交时,两条交线有什么关系?为什么?
两条交线平行.
证明:如图,因为 ,所以与没有公共点
又因为 ,所以 .
注意到 且 ,
所以与共面且没有公共点,即.
思考1
平面与平面平行的性质定理:
如果两个平行平面同时与第三个平面相交,那么它们的交线平行.
符号语言:
简记:面面平行,则线线平行.
例2 如图所示,已知都是平面,且,两条直线分别于平面相交于A,B,C和点D,E,F,求证:.
证明:如图所示,连接DC,设DC与平面β相交于点G,
则平面ACD与平面α,β分别相交于直线AD,BG,
平面DCF与平面β,γ分别相交于直线GE,CF.
因为α//β. ∴BG//AD,因此△CBG∽△CAD
同理可得
因此,
例题讲解
证明:如图所示,连接B1D1.
∵P、N分别是D1C1、B1C1的中点,
∴PN∥B1D1.∵DD1∥BB1,DD1=BB1,
∴四边形B1BDD1为平行四边形,
∴B1D1∥BD,PN∥BD.
∵PN 平面A1BD,BD 平面A1BD,∴PN∥平面A1BD
在正方体ABCD-A1B1C1D1中,M、N、P分别是C1C、B1C1、C1D1的中点,求证:平面MNP∥平面A1BD.
同理可证MN∥平面A1BD,
又PN∩MN=N,PN 平面MNP,MN 平面MNP
∴平面PMN∥平面A1BD.
练一练
1.平面α//平面β的一个充分条件是( )
A.存在一条直线a,a//α,a//β
B.存在一条直线a,a α,a//β
C.存在两条平行直线a、b,a α,b β,a//β,b//α
D.存在两条异面直线a、b,a α,b β,a//β,b//α
D
2.如图所示,在直角梯形ABCP中,BC∥AP,AB⊥BC,CD⊥AP,AD=DC=PD. E,F,G分别为线段PC,PD,BC的中点,现将△PDC折起,使点P平面ABCD.
求证:平面PAB∥平面EFG.
证明:因为PE=EC,PF=FD,所以EF∥CD,
又因为CD∥AB,
所以EF∥AB,又EF平面PAB,AB平面PAB,
所以EF∥平面PAB,同理可证EG∥平面PAB.
又因为EF∩EG=E,
所以平面PAB∥平面EFG.
