人教版五年级上册数学平行四边形的面积课件(共24张PPT)
文档属性
| 名称 | 人教版五年级上册数学平行四边形的面积课件(共24张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 4.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-01-25 06:43:01 | ||
图片预览

文档简介
(共24张PPT)
平行四边形的面积
R·五年级上册
第六单元 多边形的面积
一、情景导入
你发现了哪些图形?你会计算它们的面积吗?
长方形
平行四边形
两个花坛的面积哪个大?
长方形
平行四边形
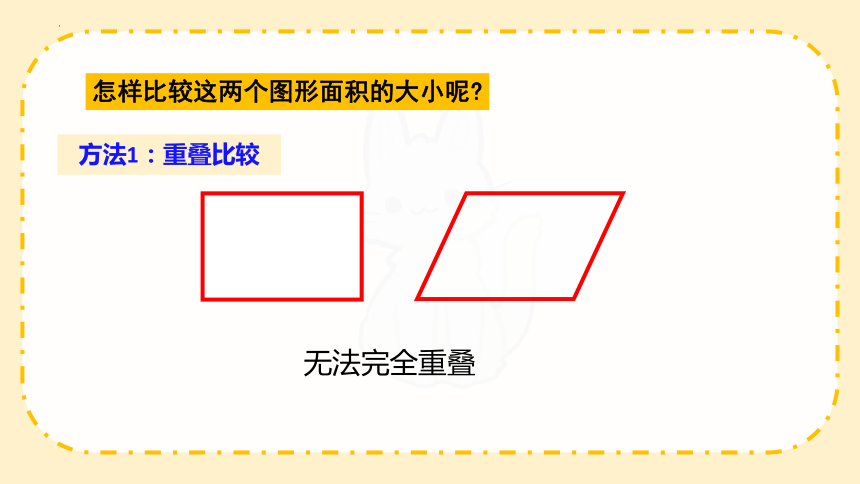
方法1:重叠比较
怎样比较这两个图形面积的大小呢
无法完全重叠
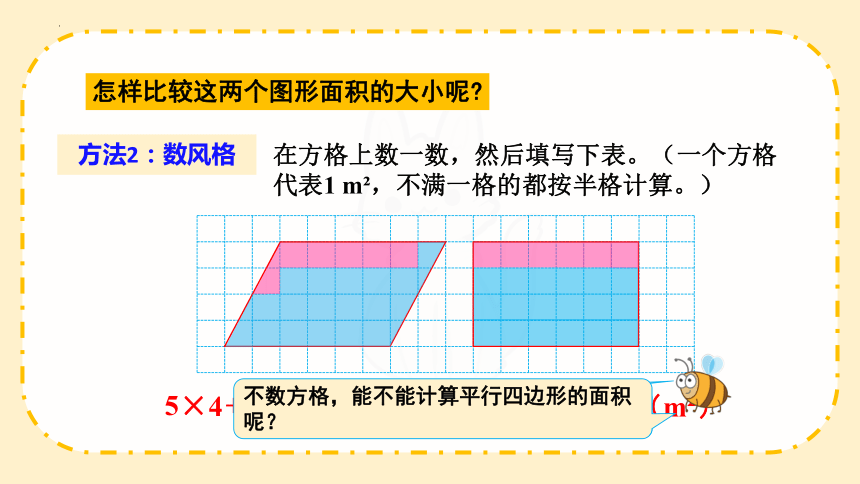
方法2:数风格
怎样比较这两个图形面积的大小呢
5
+0.5
=24(m )
=24(m )
6
×4
×4
×2
×4
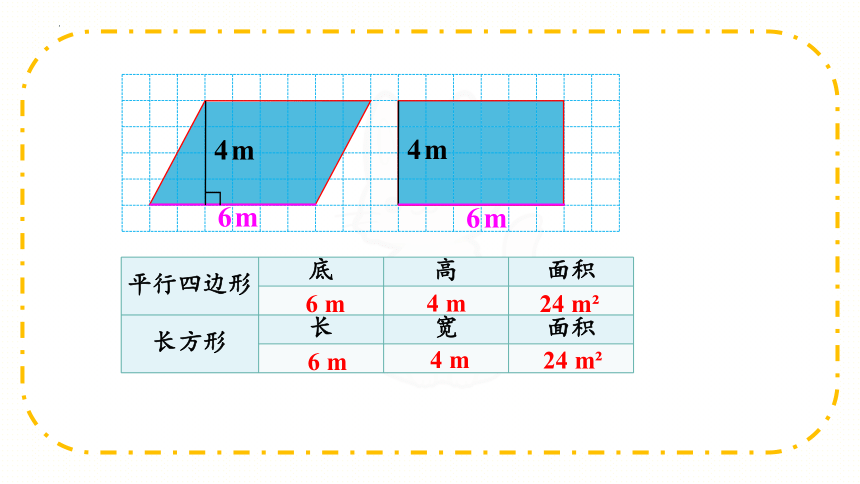
在方格上数一数,然后填写下表。(一个方格代表1 m ,不满一格的都按半格计算。)
数方格法适用于所占方格比较少的图形,有局限性。
不数方格,能不能计算平行四边形的面积呢?
6m
4m
4m
6m
平行四边形 底 高 面积
长方形 长 宽 面积
6 m
6 m
4 m
4 m
24 m
24 m
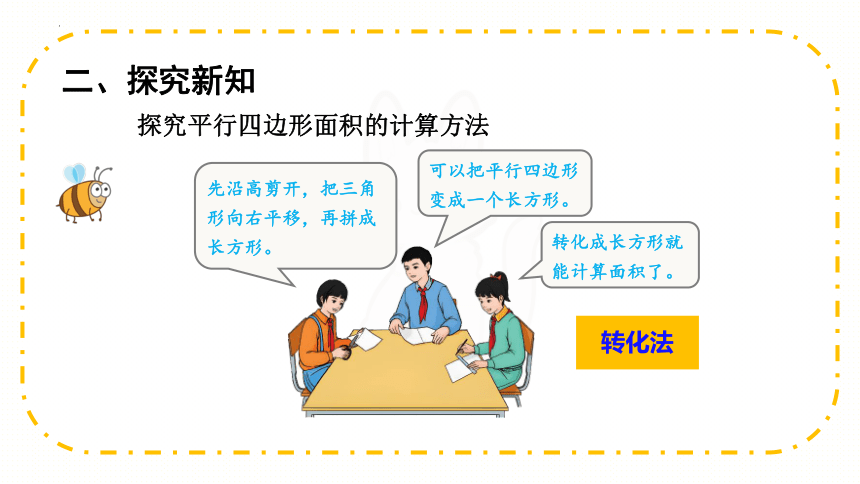
二、探究新知
先沿高剪开,把三角形向右平移,再拼成长方形。
转化法
可以把平行四边形变成一个长方形。
转化成长方形就能计算面积了。
探究平行四边形面积的计算方法
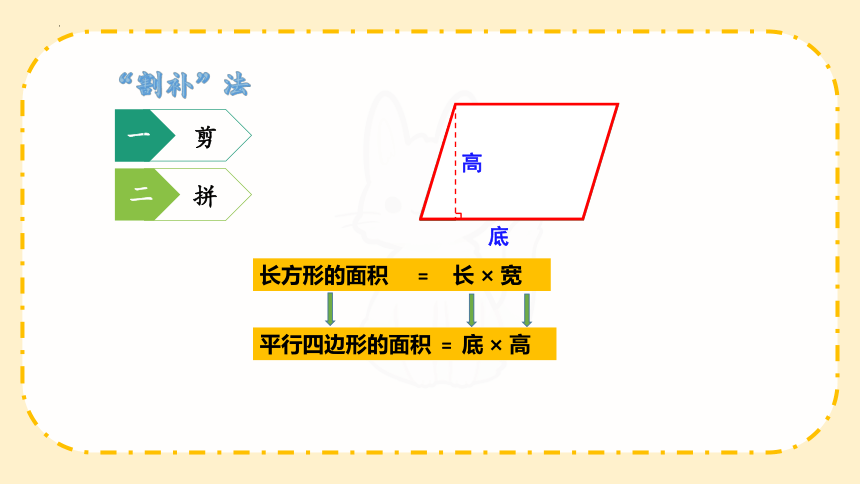
“割补”法
二
拼
一
剪
高
底
长方形的面积 = 长 × 宽
平行四边形的面积 = 底 × 高
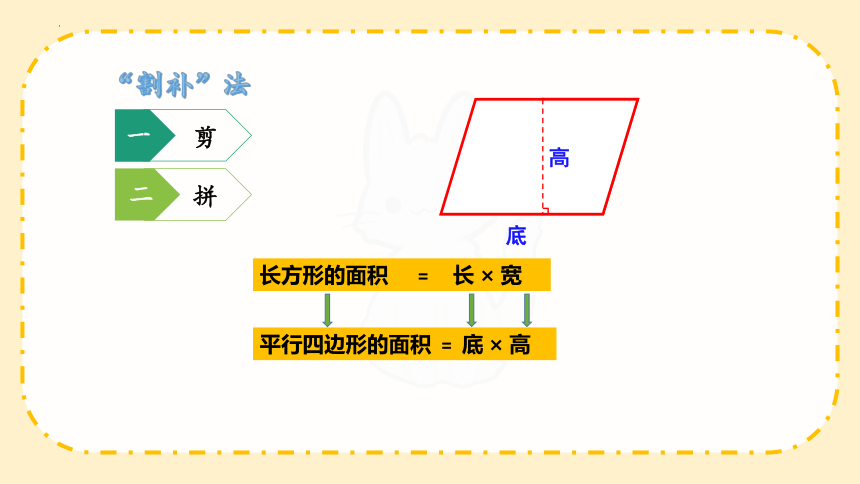
“割补”法
二
拼
一
剪
长方形的面积 = 长 × 宽
平行四边形的面积 = 底 × 高
高
底
“割补”法
二
拼
一
剪
长方形的面积 = 长 × 宽
平行四边形的面积 = 底 × 高
观察原来的平行四边形和转化后的长方形,你发现它们之间有哪些等量关系?
长方形的长相当于平行四边形的(底);
长方形的宽相当于平行四边形的(高);
这两个图形的面积相等。
长方形的面积 = 长 × 宽
平行四边形的面积 = 底 × 高
如果用 S 表示平行四边形的面积,用 a 表示平行四边形的底,用 h 表示平行四边形的高,那么平行四边形的面积计算公式可以写成:___________。
S = ah
刚才我们是怎样一步一步地研究推导出平行四边形面积的计算公式的?
平行四边形(新) 长方形(旧)
转化(割补)
推导
联系
平行四边形花坛的底是 6 m,高是 4 m,它的面积是多少?
S = ah
= 6×4
= 24(m2)
答:平行四边形花坛的面积是 24 m2。
计算平行四边形的面积时,底和高必须是对应的。
三、巩固练习
1.计算下面每个平行四边形的面积。
5.2×3.6= 18.72( cm2)
3×1.6= 4.8 ( cm2)
2×2.4=4.8 ( cm2)
2.填一填。
(1)把一个长方形木框拉成一个平行四边形,
( )不变,它的高和面积( )。
(2)平行四边形的高不变,底扩大为原来的2倍,
面积( )。
周长
改变
扩大为原来的2倍
[教材P87 练习十九 第1题]
3.一个平行四边形的停车位,它的底是6 m,高是2.5 m。这个停车位的面积是多少
S = ah
= 6×2.5
= 15(m2)
答:这个停车位的面积是 12.5 m2。
一块平行四边形的菜地,底是20 m,高是16 m,若每棵大白菜占地 0.16 m2,这块地可种多少棵大白菜
答:这块地可种2000 棵大白菜。
20×16÷0.16 = 2000 (棵)
菜地面积÷每棵菜占地面积 = 可以种的棵数
S = ah
4.
[教材P89 练习十九 第3题]
5.下表中给出的是平行四边形的底和高,计算出每个平行四边形的面积,填在空格里。
底/cm 38 70 6.2 21.5 18 0.9
高/cm 21 15 26 9.8 5.2 0.4
面积/cm2
798
1050
161.2
210.7
93.6
0.36
6. 一个平行四边形的周长是86cm(如图),以CD为底时,它的高是20cm,BC长25cm,求BC边上的高是多少厘米?
CD的长度:86÷2-25=18(cm)
平行四边形ABCD的面积:
S=ah=20×18=360(cm2)
360÷25=14.4(cm)
答:BC边上的高是14.4厘米。
2m
(10-2)×7=56(m2)
答:草坪的占地面积为56 m2。
如果将小路“抽去”,将左右两块草坪拼在一起,就得到一个长(10-2)m、宽7 m的长方形。
10 m
7 m
7.在一块长是10 m、宽是7 m的草坪中有一条小路。草坪的占地面积有多大?
四、课堂总结
同学们,这节课你们都学会了哪些知识?
平行四边形的面积
如果用 S 表示平行四边形的面积,用 a 表示平行四边形的底,用 h 表示平行四边形的高,那么平行四边形的面积计算公式可以写成:___________。
S = ah
六、作业布置
完成相关练习
平行四边形的面积
R·五年级上册
第六单元 多边形的面积
一、情景导入
你发现了哪些图形?你会计算它们的面积吗?
长方形
平行四边形
两个花坛的面积哪个大?
长方形
平行四边形
方法1:重叠比较
怎样比较这两个图形面积的大小呢
无法完全重叠
方法2:数风格
怎样比较这两个图形面积的大小呢
5
+0.5
=24(m )
=24(m )
6
×4
×4
×2
×4
在方格上数一数,然后填写下表。(一个方格代表1 m ,不满一格的都按半格计算。)
数方格法适用于所占方格比较少的图形,有局限性。
不数方格,能不能计算平行四边形的面积呢?
6m
4m
4m
6m
平行四边形 底 高 面积
长方形 长 宽 面积
6 m
6 m
4 m
4 m
24 m
24 m
二、探究新知
先沿高剪开,把三角形向右平移,再拼成长方形。
转化法
可以把平行四边形变成一个长方形。
转化成长方形就能计算面积了。
探究平行四边形面积的计算方法
“割补”法
二
拼
一
剪
高
底
长方形的面积 = 长 × 宽
平行四边形的面积 = 底 × 高
“割补”法
二
拼
一
剪
长方形的面积 = 长 × 宽
平行四边形的面积 = 底 × 高
高
底
“割补”法
二
拼
一
剪
长方形的面积 = 长 × 宽
平行四边形的面积 = 底 × 高
观察原来的平行四边形和转化后的长方形,你发现它们之间有哪些等量关系?
长方形的长相当于平行四边形的(底);
长方形的宽相当于平行四边形的(高);
这两个图形的面积相等。
长方形的面积 = 长 × 宽
平行四边形的面积 = 底 × 高
如果用 S 表示平行四边形的面积,用 a 表示平行四边形的底,用 h 表示平行四边形的高,那么平行四边形的面积计算公式可以写成:___________。
S = ah
刚才我们是怎样一步一步地研究推导出平行四边形面积的计算公式的?
平行四边形(新) 长方形(旧)
转化(割补)
推导
联系
平行四边形花坛的底是 6 m,高是 4 m,它的面积是多少?
S = ah
= 6×4
= 24(m2)
答:平行四边形花坛的面积是 24 m2。
计算平行四边形的面积时,底和高必须是对应的。
三、巩固练习
1.计算下面每个平行四边形的面积。
5.2×3.6= 18.72( cm2)
3×1.6= 4.8 ( cm2)
2×2.4=4.8 ( cm2)
2.填一填。
(1)把一个长方形木框拉成一个平行四边形,
( )不变,它的高和面积( )。
(2)平行四边形的高不变,底扩大为原来的2倍,
面积( )。
周长
改变
扩大为原来的2倍
[教材P87 练习十九 第1题]
3.一个平行四边形的停车位,它的底是6 m,高是2.5 m。这个停车位的面积是多少
S = ah
= 6×2.5
= 15(m2)
答:这个停车位的面积是 12.5 m2。
一块平行四边形的菜地,底是20 m,高是16 m,若每棵大白菜占地 0.16 m2,这块地可种多少棵大白菜
答:这块地可种2000 棵大白菜。
20×16÷0.16 = 2000 (棵)
菜地面积÷每棵菜占地面积 = 可以种的棵数
S = ah
4.
[教材P89 练习十九 第3题]
5.下表中给出的是平行四边形的底和高,计算出每个平行四边形的面积,填在空格里。
底/cm 38 70 6.2 21.5 18 0.9
高/cm 21 15 26 9.8 5.2 0.4
面积/cm2
798
1050
161.2
210.7
93.6
0.36
6. 一个平行四边形的周长是86cm(如图),以CD为底时,它的高是20cm,BC长25cm,求BC边上的高是多少厘米?
CD的长度:86÷2-25=18(cm)
平行四边形ABCD的面积:
S=ah=20×18=360(cm2)
360÷25=14.4(cm)
答:BC边上的高是14.4厘米。
2m
(10-2)×7=56(m2)
答:草坪的占地面积为56 m2。
如果将小路“抽去”,将左右两块草坪拼在一起,就得到一个长(10-2)m、宽7 m的长方形。
10 m
7 m
7.在一块长是10 m、宽是7 m的草坪中有一条小路。草坪的占地面积有多大?
四、课堂总结
同学们,这节课你们都学会了哪些知识?
平行四边形的面积
如果用 S 表示平行四边形的面积,用 a 表示平行四边形的底,用 h 表示平行四边形的高,那么平行四边形的面积计算公式可以写成:___________。
S = ah
六、作业布置
完成相关练习
