贵州省毕节市金沙县中小学2024-2025学年九年级上期末数学教学质量监测卷(含详解)
文档属性
| 名称 | 贵州省毕节市金沙县中小学2024-2025学年九年级上期末数学教学质量监测卷(含详解) |

|
|
| 格式 | docx | ||
| 文件大小 | 982.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-02-05 11:11:44 | ||
图片预览


文档简介
贵州省毕节市金沙县中小学2024-2025学年第一学期质量监测卷
九年级 数学
题号 一选择题 二填空题 17 18 19 20 21 22 23 24 25
得分
评卷人
亲爱的同学,希望你沉着、冷静、诚信地迎接学期质量监测、相信你一定能考出理想
的成绩!
一选择题(每小题 3 分,共 36 分.每小题均有 A.B.C.D 四个选项,其中只有一个选项正确,
,请用 2B铅笔在答题卡相应位置填涂)
1.将一元二次方程化为一般形式后,其中二次项系数、一次项系数、常数项分别是( )
A. B. C. D.
2.下列式子中表示是关于的反比例函数的是( )
A. B.
C. D.
3.正方形纸板在太阳光下的投影不可能是( )
A.平行四边形 B.一条线段
C.矩形 D.梯形
4.如图,已知,那么添加下列一个条件后,仍无法判定的是( )
A. B. C. D.
5.已知△ABC∽△DEF,若△ABC与△DEF的面积比为1∶9,则△ABC与△DEF的周长比为( )
A.1∶2 B.1∶3 C.1∶4 D.1∶9
6.如图,公路AC、BC互相垂直,公路AB的中点M与点C被湖隔开,若测得AB的长为4.8 km,则M、C两点间的距离为( )
A.2.4 k m B.3.6 k m C.4.2 k m D.4.8 k m
7.在一张桌子上放着几叠碗,如图.小红分别从上面、前面、左面观察所得到的图形,那么桌子上一共放着( )只碗
A.5 B.6 C.7 D.8
8中国画以墨代色,产生了墨分五色的说法,唐代张彦远《历代名画记》中曰:”运墨而五色具”,五色:即焦、浓、重、淡、清,这就是中国画用墨的奇妙处.美术老师想从这五色中先选择两色让学生重点练习,则正好选中淡与清的概率为( )
A. B. C. D.
9.从,,,这四个数中任取两个不同的数分别作为,的值,得到反比例函数,则这些反比例函数中,其图象在二、四象限的概率是( ).
A B C D
10.已知点,,是反比例函数图象上的三个点,则有( )
A. B. C. D.
11联华超市某服装专柜在销售中发现:进货价为每件50元,销售价为每件90元的某品牌童装平均每天可售出20件.为了迎接“六一”,商场决定采取适当的降价措施,扩大销售量,增加盈利.经调查发现:如果每件童装降价1元,那么平均每天就可多售出2件,要想平均每天销售这种童装盈利1200元,同时又要使顾客得到较多的实惠,设降价x元,根据题意列方程得( )
A.(40﹣x)(20+2x)=1200 B.(40﹣x)(20+x)=1200
C.(50﹣x)(20+2x)=1200 D.(90﹣x)(20+2x)=1200
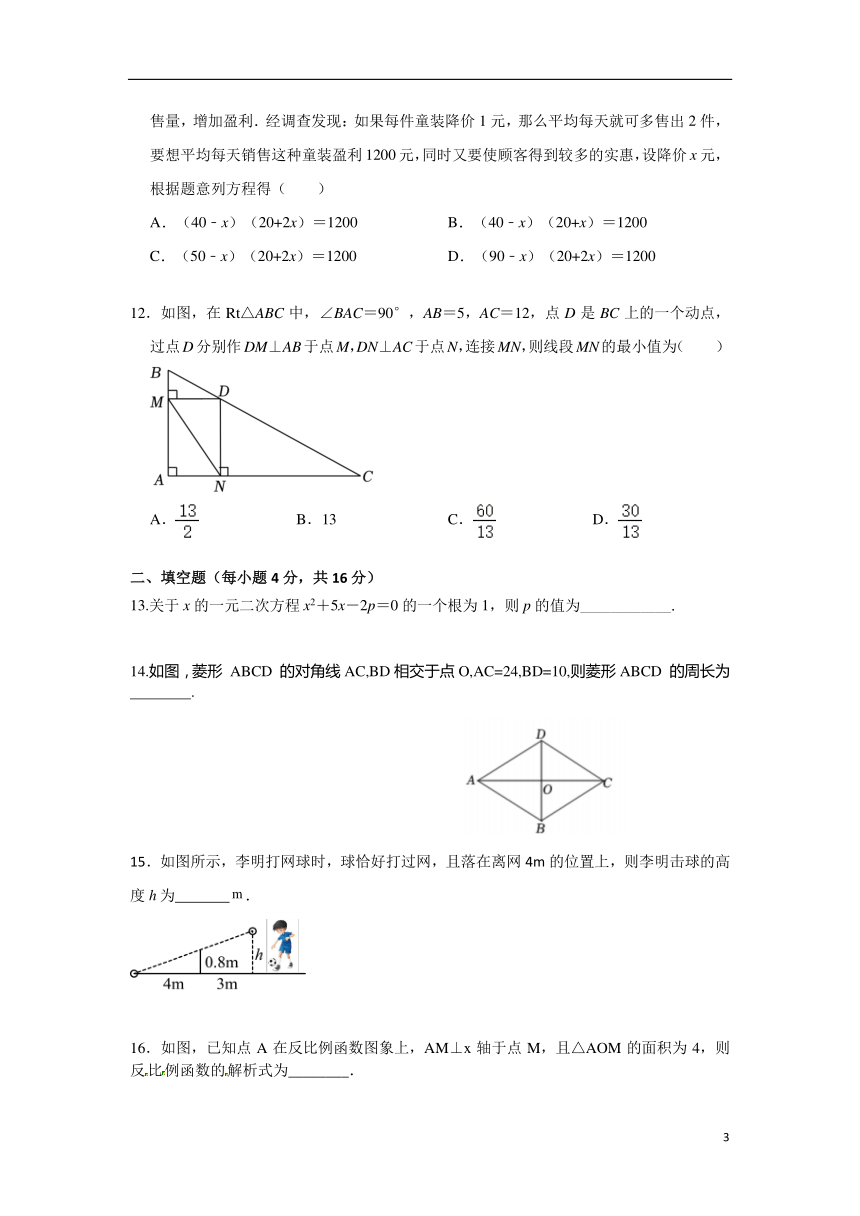
12.如图,在Rt△ABC中,∠BAC=90°,AB=5,AC=12,点D是BC上的一个动点,过点D分别作DM⊥AB于点M,DN⊥AC于点N,连接MN,则线段MN的最小值为( )
A. B.13 C. D.
二、填空题(每小题4分,共16分)
13.关于x的一元二次方程x2+5x-2p=0的一个根为1,则p的值为____________.
14.如图,菱形 ABCD 的对角线AC,BD相交于点O,AC=24,BD=10,则菱形ABCD 的周长为 .
15.如图所示,李明打网球时,球恰好打过网,且落在离网4m的位置上,则李明击球的高度h为 .
16.如图,已知点A在反比例函数图象上,AM⊥x轴于点M,且△AOM的面积为4,则反比例函数的解析式为________.
三解答题(本大题共9题,共98分,解答应写出必要的文字说明、证明过程或演算步骤)
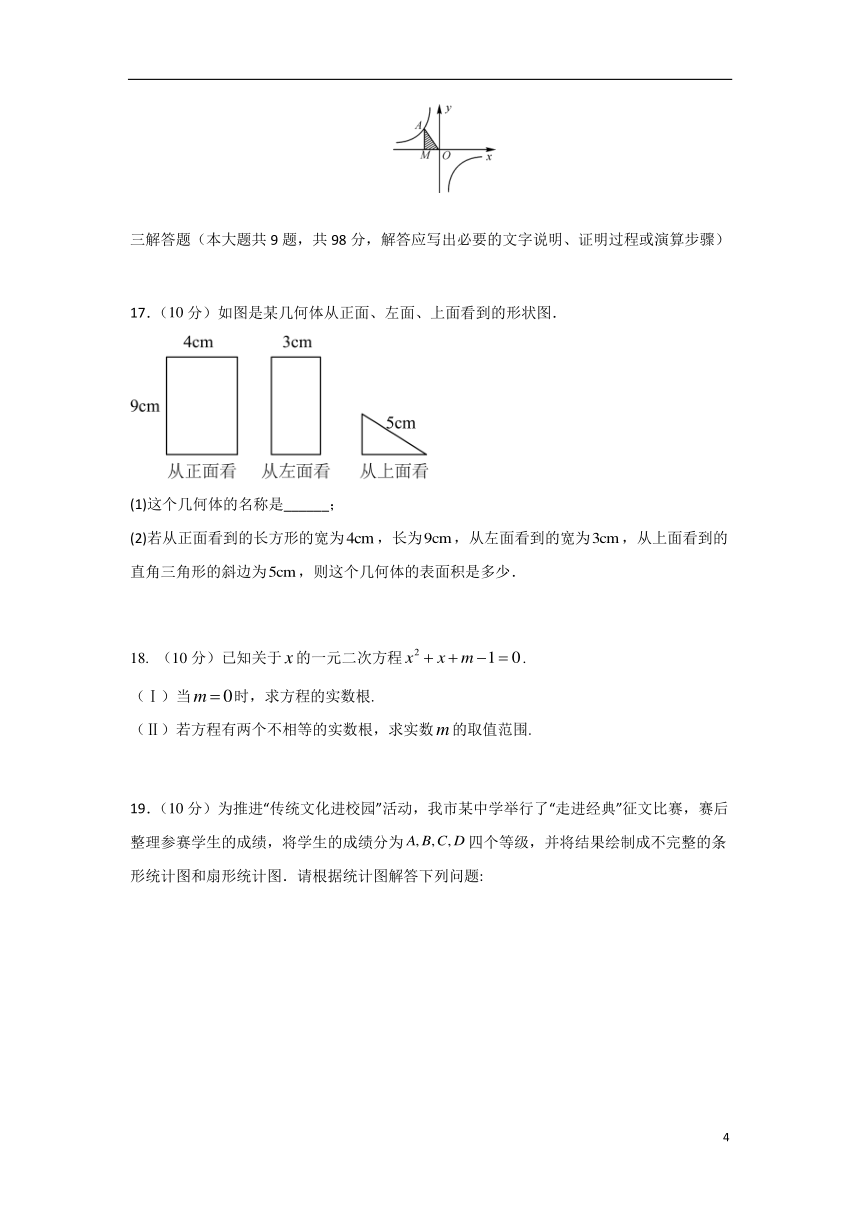
17.(10分)如图是某几何体从正面、左面、上面看到的形状图.
(1)这个几何体的名称是______;
(2)若从正面看到的长方形的宽为,长为,从左面看到的宽为,从上面看到的直角三角形的斜边为,则这个几何体的表面积是多少.
18. (10分)已知关于的一元二次方程.
(Ⅰ)当时,求方程的实数根.
(Ⅱ)若方程有两个不相等的实数根,求实数的取值范围.
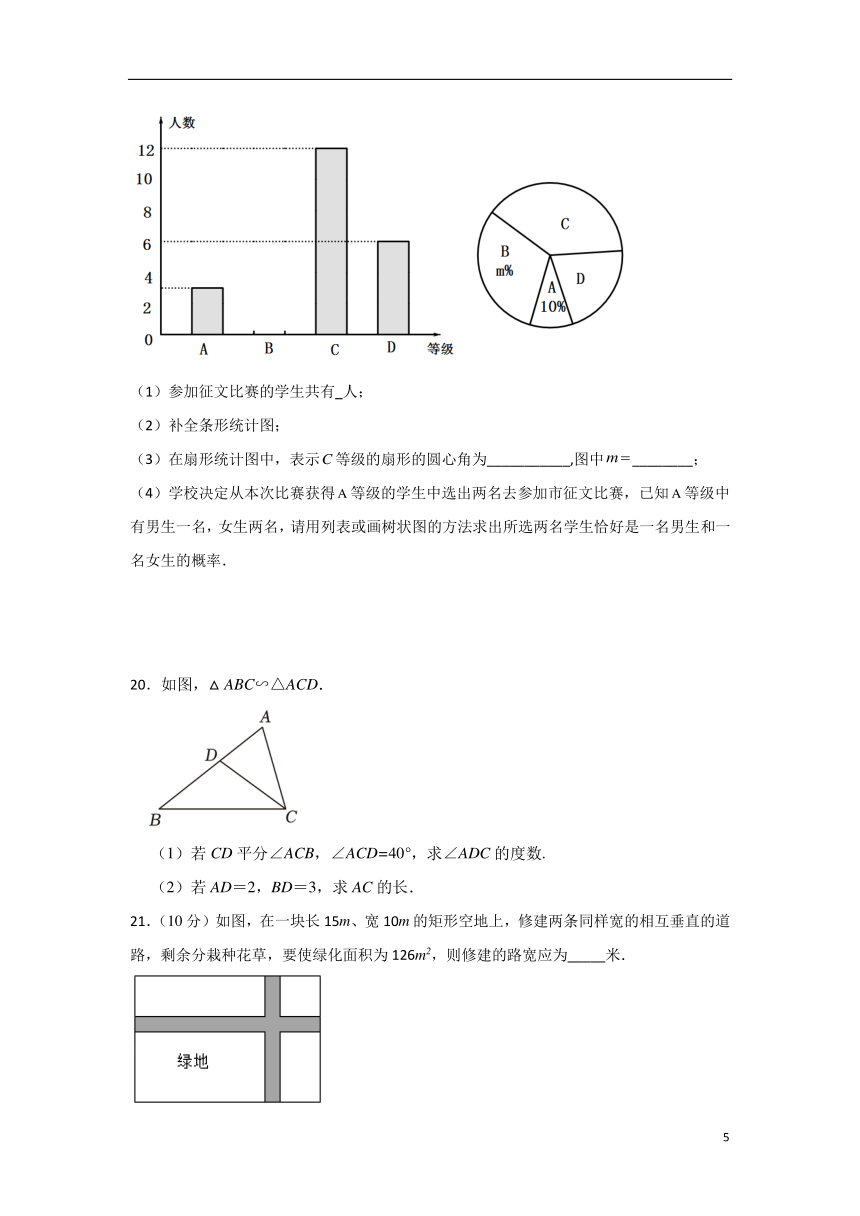
19.(10分)为推进“传统文化进校园”活动,我市某中学举行了“走进经典”征文比赛,赛后整理参赛学生的成绩,将学生的成绩分为四个等级,并将结果绘制成不完整的条形统计图和扇形统计图.请根据统计图解答下列问题:
(1)参加征文比赛的学生共有 人;
(2)补全条形统计图;
(3)在扇形统计图中,表示等级的扇形的圆心角为___________,图中________;
(4)学校决定从本次比赛获得等级的学生中选出两名去参加市征文比赛,已知等级中有男生一名,女生两名,请用列表或画树状图的方法求出所选两名学生恰好是一名男生和一名女生的概率.
20.如图,△ABC∽△ACD.
(1)若CD平分∠ACB,∠ACD=40°,求∠ADC的度数.
(2)若AD=2,BD=3,求AC的长.
21.(10分)如图,在一块长15m、宽10m的矩形空地上,修建两条同样宽的相互垂直的道路,剩余分栽种花草,要使绿化面积为126m2,则修建的路宽应为_____米.
22(12分)驾驶员血液中每毫升的酒精含量大于或等于微克即为酒驾,某研究所经实验测得,成人饮用某品牌度白酒后血液中酒精浓度微克毫升与饮酒时间小时之间函数关系如图所示当时,与成反比例.
(1)根据图象直接写出:血液中酒精浓度上升阶段的函数解析式为 ;下降阶段的函数解析式为 ;并写出的取值范围
(2)问血液中酒精浓度不低于微克毫升的持续时间是多少小时?
23.(12分)如图所示,O是矩形ABCD的对角线的交点,DE∥AC,CE∥BD.
(1)求证:OE⊥DC.
(2)若∠AOD=120°,DE=2,求矩形ABCD的面积.
24.(12分)如图,一次函数与反比例函数的图像相交于、两点.
(1)求一次函数与反比例函数的解析式;
(2)直接写出不等式的解集;
(3)求△AOB面积.
25(12分)数学实验,能增加学习数学的乐趣,还能经历知识“再创造”的过程,更是培养动手能力,创新能力的一种手段.小强在学习《相似》一章中对“直角三角形斜边上作高”这一基本图形(如图1)产生了如下问题,请同学们帮他解决.
在 中,点为边上一点,连接.
初步探究,
如图2,若,求证:;
(2)尝试应用
如图3,在(1)的条件下,若点为中点,,求的长;
九年级 数学
参考答案
一选择题(每小题 3 分,共 36 分
1【答案】C
【解析】先把方程化为一般式,所以二次项系数、一次项系数、常数项分别是3,-5,-1,可得答案。
2【答案】C
【解析】A,是正比例函数,此选项错误;
B,是正比例函数,此选项错误;
C,是反比例函数,此选项正确;
D,是一次函数,此选项错误。
故选C。
3【答案】D
【解析】一张正方形纸板在太阳光线的照射下,形成的影子不可能是梯形,故选D
4【答案】A
【解析】
都可判定,选项中不是夹这两个角的边,所以不相似,故选
5【答案】B
【解析】△ABC∽△DEF, 且面积比为1∶9 △ABC与△DEF的相似比为.1∶3, △ABC与△DEF,的周长比为.1∶3.故选B
6【答案】A
【解析】有题意,为的中点,,,,即两点间的距离为,故选:A
7【答案】C
【解析】
由上面看到的形状可知一共有3叠碗,(只),所以桌子上一共放着7只碗.
故选:C
8【答案】C.
【解析】
共有20种等可能的结果,其中正好选中淡与清的结果有:(淡,清),(清,淡),共2种,正好选中淡与清的概率为, ,故选:C.
9【答案】A
则共有12种等可能的结果,反比例函数中,图像在二、四象限,所以,有8种符合条件的结果,所以(图像在二、四象限)。故选 : A
10【答案】D
【解析】
反比例函数图像的两个分支在第二四象限,且在每个象限内随的增大而增大;又是双曲线上的两点,且,又点在第二象限故选 : D :
11【答案】A
【解析】
设每件童装应降价元,由题意,得,即:,故选
12【答案】C
【解析】
由勾股定理求出的长,再证明四边形是矩形,可得,根据垂线段最短和三角形面积即可解决问题,故选:C.
二填空题(每小题4分,共16分)
13【答案】3
14【答案】52
【解析】
菱形的四条边相等,要求周长,只需求出边长即可,菱形的对角线互相平分,根据勾股定理求边长即可。
15【答案】1.4
16【答案】
【解析】
三解答题(本大题共9题,共98分)
17(10分)【解析】
只有棱柱的主视图和左视图才可能出现长方形,根据俯视图是三角形,可得到此几何体为三棱柱;
3条长9cm的高,加上两个三角形的周长就是几何体的所有棱长和;三个长为9cm,宽分别为3cm、4cm、5cm的长方形的面积与两个直角三角形的面积和就是表面积。
(1)解:这个几何体是三棱柱.
故答案为:三棱柱.
(2)解:这个几何体的所有棱长的和(cm).
表面积.
18(10分)【解析】
令,用公式法求出一元二次方程的根即可;
根据方程有两个不相等的实数根,计算根的判别式得关于的不等式,求解不等式即可。
解:(Ⅰ)当时,方程为.
.
∴,
∴,.
(Ⅱ)∵方程有两个不相等的实数根,
∴
即
∵∴.
19(10分)【解析】
解:(1)根据题意得成绩为A等级的学生有3人,所占的百分比为10%,
则3÷10%=30,
即参加征文比赛的学生共有30人;
(2)由条形统计图可知A、C、D等级的人数分别为3人、12人、6人,
则30 3 12 6=9(人),即B等级的人数为9人,补全条形统计图如下图
(3), ,∴m=30
(4)依题意,列表如下:
男 女 女
男 (男,女) (男,女)
女 (男,女) (女,女)
女 (男,女) (女,女)
由上表可知总共有6种结果,每种结果出现的可能性相同,其中所选两名学生恰好是一男一女的结果共有4种,所以;
或树状图如下
由上图可知总共有6种结果,每种结果出现的可能性相同,其中所选两名学生恰好是一男一女的结果共有4种,所以.
20(10分)【解析】
根据相似三角形的性质以及角平分线的定义得出与的度数,再根据三角形外角的性质即可求解;
根据相似三角形的性质得出等式求出的长即可求解。
解:(1)∵CD平分∠ACB,∠ACD=40°
∴∠ACD=∠BCD=40°
∵△ABC∽△ACD
∴∠ABC=∠ACD=40°
∴∠ADC=80°
(2)∵CD=2,BD=3
∴AB=5
∵△ABC∽△ACD
∴
∴,
21(10分)【解析】
把所修的两条道路分别平移到矩形的最上边和最左边,则剩下的草坪是一个长方形,根据长方形的面积公式列方程求解即可。
解:设道路的宽为x m,根据题意得:
(10﹣x)(15﹣x)=126,
解得:x1=1,x2=24(不合题意,舍去),
答:道路的宽应为1米;
22(12分)【解析】
利用待定系数法求解即可;
根据(1)所求分别求出时和时,的值即可得到答案。
解:(1);
(2)当,则,
解得:,
当,则,
解得:,
小时,
血液中药物浓度不低于微克毫升的持续时间小时.
23(12分)【解析】
先证四边形ODEC是平行四边形,再证四边形ODEC是菱形;
求出的长,根据矩形的面积公式即可求解。
(1)证明:
∵DE∥AC,CE∥BD,
∴DE∥OC,CE∥OD,
∴四边形ODEC是平行四边形,
∵四边形ABCD是矩形,
∴OD=OC=OA=OB,
∴四边形ODEC是平行四边形,∴OE⊥DC,
(2)∵DE=2,且四边形ODEC是菱形
∴OD=OC=DE=2=OA,
∴AC=4
∵∠AOD=120,AO=DO
∴∠DAO=30°,且∠ADC=90°
∴CD=2,AD=CD=2
∴S矩形ABCD=2×2=4
24(12分)【解析】
利用待定系数法计算解析式即可;
利用数形结合思想,结合交点的横坐标计算即可;
设直线与轴的交点为,利用直线的解析式计算,结合计算即可。
解:(1)∵一次函数与反比例函数的图像相交于、两点,
∴
,
解得,
故;.
(2)∵,,且,
故或.
(3)设直线与y轴的交点为C,
∵,
∴,
∴,
∵,,
∴.
25(12分)【解析】
解:(1)证明:∵,,
∴,
∴,
∴;
(2)∵点为中点,
∴设,
由(1)知,
∴,
∴,
∴与的相似比为,
∴,
∵
∴;
九年级 数学
题号 一选择题 二填空题 17 18 19 20 21 22 23 24 25
得分
评卷人
亲爱的同学,希望你沉着、冷静、诚信地迎接学期质量监测、相信你一定能考出理想
的成绩!
一选择题(每小题 3 分,共 36 分.每小题均有 A.B.C.D 四个选项,其中只有一个选项正确,
,请用 2B铅笔在答题卡相应位置填涂)
1.将一元二次方程化为一般形式后,其中二次项系数、一次项系数、常数项分别是( )
A. B. C. D.
2.下列式子中表示是关于的反比例函数的是( )
A. B.
C. D.
3.正方形纸板在太阳光下的投影不可能是( )
A.平行四边形 B.一条线段
C.矩形 D.梯形
4.如图,已知,那么添加下列一个条件后,仍无法判定的是( )
A. B. C. D.
5.已知△ABC∽△DEF,若△ABC与△DEF的面积比为1∶9,则△ABC与△DEF的周长比为( )
A.1∶2 B.1∶3 C.1∶4 D.1∶9
6.如图,公路AC、BC互相垂直,公路AB的中点M与点C被湖隔开,若测得AB的长为4.8 km,则M、C两点间的距离为( )
A.2.4 k m B.3.6 k m C.4.2 k m D.4.8 k m
7.在一张桌子上放着几叠碗,如图.小红分别从上面、前面、左面观察所得到的图形,那么桌子上一共放着( )只碗
A.5 B.6 C.7 D.8
8中国画以墨代色,产生了墨分五色的说法,唐代张彦远《历代名画记》中曰:”运墨而五色具”,五色:即焦、浓、重、淡、清,这就是中国画用墨的奇妙处.美术老师想从这五色中先选择两色让学生重点练习,则正好选中淡与清的概率为( )
A. B. C. D.
9.从,,,这四个数中任取两个不同的数分别作为,的值,得到反比例函数,则这些反比例函数中,其图象在二、四象限的概率是( ).
A B C D
10.已知点,,是反比例函数图象上的三个点,则有( )
A. B. C. D.
11联华超市某服装专柜在销售中发现:进货价为每件50元,销售价为每件90元的某品牌童装平均每天可售出20件.为了迎接“六一”,商场决定采取适当的降价措施,扩大销售量,增加盈利.经调查发现:如果每件童装降价1元,那么平均每天就可多售出2件,要想平均每天销售这种童装盈利1200元,同时又要使顾客得到较多的实惠,设降价x元,根据题意列方程得( )
A.(40﹣x)(20+2x)=1200 B.(40﹣x)(20+x)=1200
C.(50﹣x)(20+2x)=1200 D.(90﹣x)(20+2x)=1200
12.如图,在Rt△ABC中,∠BAC=90°,AB=5,AC=12,点D是BC上的一个动点,过点D分别作DM⊥AB于点M,DN⊥AC于点N,连接MN,则线段MN的最小值为( )
A. B.13 C. D.
二、填空题(每小题4分,共16分)
13.关于x的一元二次方程x2+5x-2p=0的一个根为1,则p的值为____________.
14.如图,菱形 ABCD 的对角线AC,BD相交于点O,AC=24,BD=10,则菱形ABCD 的周长为 .
15.如图所示,李明打网球时,球恰好打过网,且落在离网4m的位置上,则李明击球的高度h为 .
16.如图,已知点A在反比例函数图象上,AM⊥x轴于点M,且△AOM的面积为4,则反比例函数的解析式为________.
三解答题(本大题共9题,共98分,解答应写出必要的文字说明、证明过程或演算步骤)
17.(10分)如图是某几何体从正面、左面、上面看到的形状图.
(1)这个几何体的名称是______;
(2)若从正面看到的长方形的宽为,长为,从左面看到的宽为,从上面看到的直角三角形的斜边为,则这个几何体的表面积是多少.
18. (10分)已知关于的一元二次方程.
(Ⅰ)当时,求方程的实数根.
(Ⅱ)若方程有两个不相等的实数根,求实数的取值范围.
19.(10分)为推进“传统文化进校园”活动,我市某中学举行了“走进经典”征文比赛,赛后整理参赛学生的成绩,将学生的成绩分为四个等级,并将结果绘制成不完整的条形统计图和扇形统计图.请根据统计图解答下列问题:
(1)参加征文比赛的学生共有 人;
(2)补全条形统计图;
(3)在扇形统计图中,表示等级的扇形的圆心角为___________,图中________;
(4)学校决定从本次比赛获得等级的学生中选出两名去参加市征文比赛,已知等级中有男生一名,女生两名,请用列表或画树状图的方法求出所选两名学生恰好是一名男生和一名女生的概率.
20.如图,△ABC∽△ACD.
(1)若CD平分∠ACB,∠ACD=40°,求∠ADC的度数.
(2)若AD=2,BD=3,求AC的长.
21.(10分)如图,在一块长15m、宽10m的矩形空地上,修建两条同样宽的相互垂直的道路,剩余分栽种花草,要使绿化面积为126m2,则修建的路宽应为_____米.
22(12分)驾驶员血液中每毫升的酒精含量大于或等于微克即为酒驾,某研究所经实验测得,成人饮用某品牌度白酒后血液中酒精浓度微克毫升与饮酒时间小时之间函数关系如图所示当时,与成反比例.
(1)根据图象直接写出:血液中酒精浓度上升阶段的函数解析式为 ;下降阶段的函数解析式为 ;并写出的取值范围
(2)问血液中酒精浓度不低于微克毫升的持续时间是多少小时?
23.(12分)如图所示,O是矩形ABCD的对角线的交点,DE∥AC,CE∥BD.
(1)求证:OE⊥DC.
(2)若∠AOD=120°,DE=2,求矩形ABCD的面积.
24.(12分)如图,一次函数与反比例函数的图像相交于、两点.
(1)求一次函数与反比例函数的解析式;
(2)直接写出不等式的解集;
(3)求△AOB面积.
25(12分)数学实验,能增加学习数学的乐趣,还能经历知识“再创造”的过程,更是培养动手能力,创新能力的一种手段.小强在学习《相似》一章中对“直角三角形斜边上作高”这一基本图形(如图1)产生了如下问题,请同学们帮他解决.
在 中,点为边上一点,连接.
初步探究,
如图2,若,求证:;
(2)尝试应用
如图3,在(1)的条件下,若点为中点,,求的长;
九年级 数学
参考答案
一选择题(每小题 3 分,共 36 分
1【答案】C
【解析】先把方程化为一般式,所以二次项系数、一次项系数、常数项分别是3,-5,-1,可得答案。
2【答案】C
【解析】A,是正比例函数,此选项错误;
B,是正比例函数,此选项错误;
C,是反比例函数,此选项正确;
D,是一次函数,此选项错误。
故选C。
3【答案】D
【解析】一张正方形纸板在太阳光线的照射下,形成的影子不可能是梯形,故选D
4【答案】A
【解析】
都可判定,选项中不是夹这两个角的边,所以不相似,故选
5【答案】B
【解析】△ABC∽△DEF, 且面积比为1∶9 △ABC与△DEF的相似比为.1∶3, △ABC与△DEF,的周长比为.1∶3.故选B
6【答案】A
【解析】有题意,为的中点,,,,即两点间的距离为,故选:A
7【答案】C
【解析】
由上面看到的形状可知一共有3叠碗,(只),所以桌子上一共放着7只碗.
故选:C
8【答案】C.
【解析】
共有20种等可能的结果,其中正好选中淡与清的结果有:(淡,清),(清,淡),共2种,正好选中淡与清的概率为, ,故选:C.
9【答案】A
则共有12种等可能的结果,反比例函数中,图像在二、四象限,所以,有8种符合条件的结果,所以(图像在二、四象限)。故选 : A
10【答案】D
【解析】
反比例函数图像的两个分支在第二四象限,且在每个象限内随的增大而增大;又是双曲线上的两点,且,又点在第二象限故选 : D :
11【答案】A
【解析】
设每件童装应降价元,由题意,得,即:,故选
12【答案】C
【解析】
由勾股定理求出的长,再证明四边形是矩形,可得,根据垂线段最短和三角形面积即可解决问题,故选:C.
二填空题(每小题4分,共16分)
13【答案】3
14【答案】52
【解析】
菱形的四条边相等,要求周长,只需求出边长即可,菱形的对角线互相平分,根据勾股定理求边长即可。
15【答案】1.4
16【答案】
【解析】
三解答题(本大题共9题,共98分)
17(10分)【解析】
只有棱柱的主视图和左视图才可能出现长方形,根据俯视图是三角形,可得到此几何体为三棱柱;
3条长9cm的高,加上两个三角形的周长就是几何体的所有棱长和;三个长为9cm,宽分别为3cm、4cm、5cm的长方形的面积与两个直角三角形的面积和就是表面积。
(1)解:这个几何体是三棱柱.
故答案为:三棱柱.
(2)解:这个几何体的所有棱长的和(cm).
表面积.
18(10分)【解析】
令,用公式法求出一元二次方程的根即可;
根据方程有两个不相等的实数根,计算根的判别式得关于的不等式,求解不等式即可。
解:(Ⅰ)当时,方程为.
.
∴,
∴,.
(Ⅱ)∵方程有两个不相等的实数根,
∴
即
∵∴.
19(10分)【解析】
解:(1)根据题意得成绩为A等级的学生有3人,所占的百分比为10%,
则3÷10%=30,
即参加征文比赛的学生共有30人;
(2)由条形统计图可知A、C、D等级的人数分别为3人、12人、6人,
则30 3 12 6=9(人),即B等级的人数为9人,补全条形统计图如下图
(3), ,∴m=30
(4)依题意,列表如下:
男 女 女
男 (男,女) (男,女)
女 (男,女) (女,女)
女 (男,女) (女,女)
由上表可知总共有6种结果,每种结果出现的可能性相同,其中所选两名学生恰好是一男一女的结果共有4种,所以;
或树状图如下
由上图可知总共有6种结果,每种结果出现的可能性相同,其中所选两名学生恰好是一男一女的结果共有4种,所以.
20(10分)【解析】
根据相似三角形的性质以及角平分线的定义得出与的度数,再根据三角形外角的性质即可求解;
根据相似三角形的性质得出等式求出的长即可求解。
解:(1)∵CD平分∠ACB,∠ACD=40°
∴∠ACD=∠BCD=40°
∵△ABC∽△ACD
∴∠ABC=∠ACD=40°
∴∠ADC=80°
(2)∵CD=2,BD=3
∴AB=5
∵△ABC∽△ACD
∴
∴,
21(10分)【解析】
把所修的两条道路分别平移到矩形的最上边和最左边,则剩下的草坪是一个长方形,根据长方形的面积公式列方程求解即可。
解:设道路的宽为x m,根据题意得:
(10﹣x)(15﹣x)=126,
解得:x1=1,x2=24(不合题意,舍去),
答:道路的宽应为1米;
22(12分)【解析】
利用待定系数法求解即可;
根据(1)所求分别求出时和时,的值即可得到答案。
解:(1);
(2)当,则,
解得:,
当,则,
解得:,
小时,
血液中药物浓度不低于微克毫升的持续时间小时.
23(12分)【解析】
先证四边形ODEC是平行四边形,再证四边形ODEC是菱形;
求出的长,根据矩形的面积公式即可求解。
(1)证明:
∵DE∥AC,CE∥BD,
∴DE∥OC,CE∥OD,
∴四边形ODEC是平行四边形,
∵四边形ABCD是矩形,
∴OD=OC=OA=OB,
∴四边形ODEC是平行四边形,∴OE⊥DC,
(2)∵DE=2,且四边形ODEC是菱形
∴OD=OC=DE=2=OA,
∴AC=4
∵∠AOD=120,AO=DO
∴∠DAO=30°,且∠ADC=90°
∴CD=2,AD=CD=2
∴S矩形ABCD=2×2=4
24(12分)【解析】
利用待定系数法计算解析式即可;
利用数形结合思想,结合交点的横坐标计算即可;
设直线与轴的交点为,利用直线的解析式计算,结合计算即可。
解:(1)∵一次函数与反比例函数的图像相交于、两点,
∴
,
解得,
故;.
(2)∵,,且,
故或.
(3)设直线与y轴的交点为C,
∵,
∴,
∴,
∵,,
∴.
25(12分)【解析】
解:(1)证明:∵,,
∴,
∴,
∴;
(2)∵点为中点,
∴设,
由(1)知,
∴,
∴,
∴与的相似比为,
∴,
∵
∴;
同课章节目录
