贵州省毕节市金沙县中小学2024-2025学年八年级上期末教学质量监测卷(含详解)
文档属性
| 名称 | 贵州省毕节市金沙县中小学2024-2025学年八年级上期末教学质量监测卷(含详解) |  | |
| 格式 | docx | ||
| 文件大小 | 579.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-02-05 11:09:34 | ||
图片预览




文档简介
贵州省毕节市金沙县中小学 2024-2025 学年第一学期质量监测卷
八年级 数学
题号 一选择题 二填空题 17 18 19 20 21 22 23 24 25
得分
评卷人
亲爱的同学,希望你沉着、冷静、诚信地迎接学期质量监测、相信你一定能考出理想
的成绩!
一选择题(每小题 3 分,共 36 分.每小题均有 A.B.C.D 四个选项,其中只有一个选项正确,
,请用 2B铅笔在答题卡相应位置填涂)
1. -8的立方根是( )
A. 2 B. -2 C. ±2 D. -4
2 下列每组数表示三条线段长,其中可以构成直角三角形的一组线段是( )
A. 1,2,3 B. 2,3,4 C. 3,4,5 D. 4,5,6
3.在平面直角坐标系中,点P(﹣3,5)关于x轴的对称点在( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
4.下列y关于x的函数关系式:① y=x;②y= ;③y= -1;④y= -x+10其中一次函数的个数是( )
A.4 B.3 C.2 D.1
5.刘翔在出征北京奥运会前刻苦进行110米跨栏训练,教练对他20次的训练成绩进行统计分析,判断他的成绩是否稳定,则教练需要知道刘翔这20次成绩的( )
A.众数 B.平均数 C.频数 D.方差
6 小丽在用“加减消元法”解二元一次方程组时,利用消去,则、的值可能是( )
A. , B. , C. , D. ,
7.如图,将直尺与含30°角的三角尺摆放在一起,若∠1=20°,则∠2的度数是( )
A.30° B.40° C.50° D.60°
8 若,则等于( )
A. 1 B. 5 C. D.
9. 小张参加了某公司的招聘考试,考试分面试和笔试(成绩均按百分制),面试占60%,笔试占40%,小张的面试和笔试成绩分别为92分和90分,则小张的综合成绩为( ).
A 91.2分 B 92分 C 90 分 D 91 分
10 已知 a,b满足方程组 ,则 a+b的值为( )
A. 2 B. 3 C. 4 D. 5
11.如图,直线l1:y=2x+1与直线l2:y=mx+n相交于点P(1,b),则关于x,y的方程组的解为( )
A. B. C. D.
12 如图,在平面直角坐标系中,一动点从原点O出发,按向上、向右、向下、向右的方向不断地移动,每移动一个单位,得到点A1(0,1)、A2(1,1)、A3(1,0)、A4(2,0)…,那么点A2023的坐标为( )
A.(1011,0) B. (1011,1)
C. (2022,0) D. (2022,1)
二填空题(每小题4分,共16分)
13. 若点在y轴上,则点M的坐标是________.
14.已知一次函数,若y随x的增大而减小,那么m的取值范围是 .
15. 第24届冬季奥林匹克运动会将于2022年02月04日至2022年02月20日在中华人民共和国北京市和张家口市联合举行,这是中国历史上第一次举办冬季奥运会冬奥会吉祥物“冰墩墩”和“雪容融”陶制品分为小套装和大套装两种已知购买2个小套装和购买1个大套装,共需220元;购买3个小套装和2个大套装,共需390元,则大套装的单价为____________元
16.如图,已知圆柱体底面圆的半径为,高为2,AB、CD分别是两底面的直径,AD,BC是母线.若一只蚂蚁从A点出发,从侧面爬行到C点,则蚂蚁爬行的最短路线的长度是 .(结果保留根式)
三解答题(本大题共9题,共98分,解答应写出必要的文字说明、证明过程或演算步骤)
17. (10分)计算:(1).
(2);
18 (10分)解下列方程组
(2)小明求得方程组的解为,由于不小心,滴上了墨水,刚好遮住了两个数和,求这两个数.
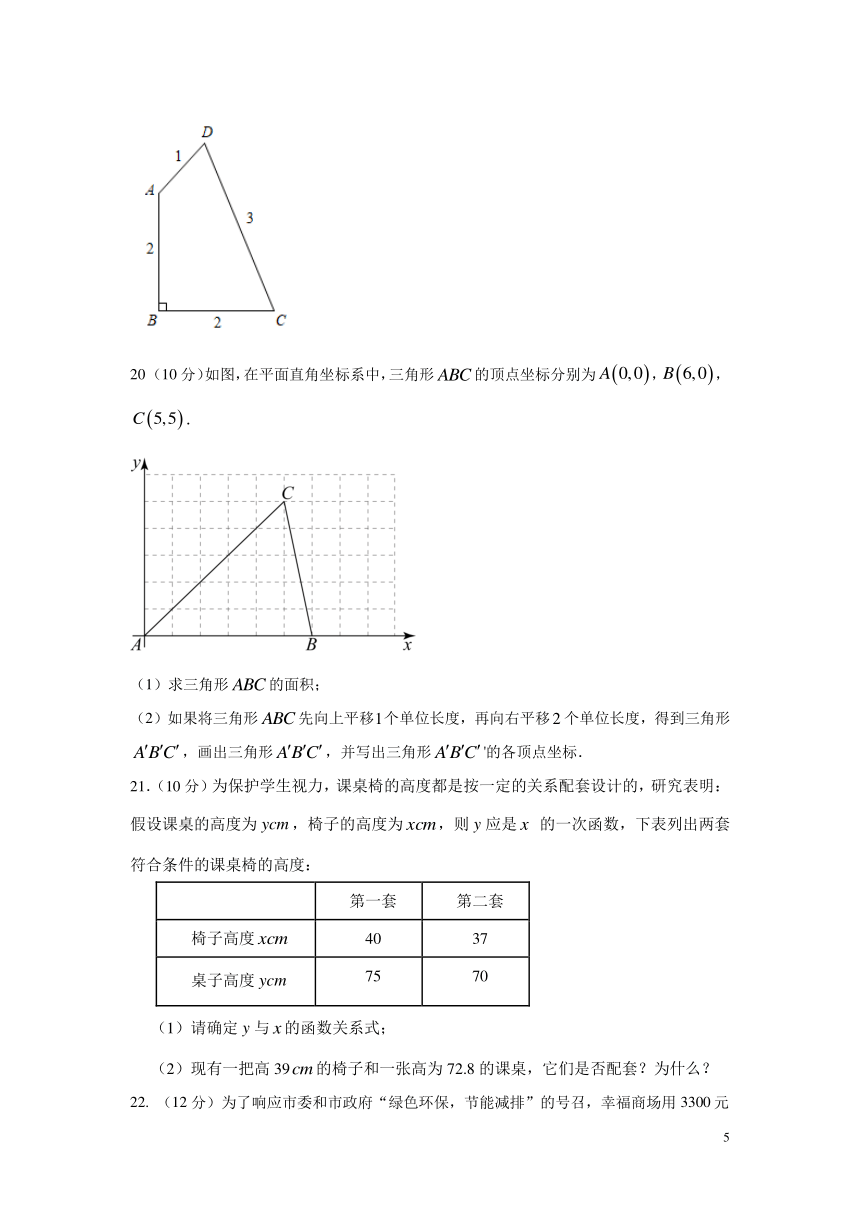
19 (10分)有一块薄铁皮ABCD,∠B=90°,各边的尺寸如图所示,若沿对角线AC剪开,得到的两块都是“直角三角形”形状吗?为什么?
20 (10分)如图,在平面直角坐标系中,三角形的顶点坐标分别为,,.
(1)求三角形的面积;
(2)如果将三角形先向上平移个单位长度,再向右平移个单位长度,得到三角形,画出三角形,并写出三角形'的各顶点坐标.
21.(10分)为保护学生视力,课桌椅的高度都是按一定的关系配套设计的,研究表明:假设课桌的高度为,椅子的高度为,则应是 的一次函数,下表列出两套符合条件的课桌椅的高度:
第一套 第二套
椅子高度 40 37
桌子高度 75 70
(1)请确定与的函数关系式;
(2)现有一把高39的椅子和一张高为72.8的课桌,它们是否配套?为什么?
22. (12分)为了响应市委和市政府“绿色环保,节能减排”的号召,幸福商场用3300元购进甲、乙两种节能灯共计100只,很快售完.这两种节能灯的进价、售价如下表:
进价(元只) 售价(元只)
甲种节能灯 30 40
乙种节能灯 35 50
(1)求幸福商场甲、乙两种节能灯各购进了多少只?
(2)全部售完100只节能灯后,商场共计获利多少元?
23. (12分)八(1)班组织了一次经典朗读比赛,甲、乙两队各10人的比赛成绩如下表
甲 7 8 9 7 10 10 9 10 10 10
乙 10 8 7 9 8 10 10 9 10 9
(1)甲队成绩的中位数是 分,乙队成绩的众数是 分;
(2)计算甲队的平均成绩和方差;
(3)成绩较为整齐的是哪个队?
24.(12分)平面内的两条直线有相交和平行两种位置关系.
(1)AB平行于CD.如图a,点P在AB,CD的外部时,由AB∥CD,有∠B=∠BOD,又因∠BOD是△POD的外角,故∠BOD=∠BPD+∠D,故∠BPD=∠B﹣∠D.
(2)如图b,将点P移到AB,CD的内部,以上结论是否成立?若不成立,则∠BPD,∠B,∠D之间有何数量关系?请证明你的结论;
25. (12分)如图,直线表达式为,点,的坐标分别为,,直线与直线相交于点.
(1)求直线的表达式:
(2)求点的坐标;
(3)若在轴上存在一点,使得的面积是的面积的倍,请直接写出点的坐标.
八年级 数学
参考答案
一选择题(每小题 3 分,共 36 分
1【答案】B
【解析】
根据立方根的定义直接得到答案
2【答案】C
【解析】根据勾股定理的逆定理,只有 中,能构成直角三角形,,故选
3【答案】C
【解析】直接利用关于轴对称点的性质得出答案。
4【答案】C
【解析】① y=x是正比例函数,是特殊的一次函数;
②y= 属于二次函数;
③y= -1不属于一次函数
④y= -x+10是一次函数。
综上所述,一次函数的个数是2个。故选:
5【答案】D
【解析】
众数 、平均数是反映一组数据的集中趋势,而频数是数据出现的次数,只有方差是反映数据的波动大小的。故为了判断成绩的稳定,需要知道的是方差。故选D
6【答案】D
【解析】为了消去,应使的系数互为相反数,由题意可知D正确
7【答案】C
【解析】
先根据三角形外角的性质,再根据平行线的性质得到∠2的度数.
8【答案】A
【解析】
根据二次根式有意义的条件得= 2,从而求得=—3,进而解决此题.
9【答案】A
【解析】
根据加权平均数的定义列式计算即可,
10【答案】C
【解析】
两式相加得 3a+3b-12,系数化为 1 即可解得.
11【答案】C
【解析】
首先利用y = 2x+ 1得到P点坐标,再根据两函数图象的交点坐标就是两函数组成的二元一次方程组的解可得答案.
12【答案】A
二填空题(每小题4分,共16分)
13【答案】
【解析】
直接利用y轴上点的坐标特点求出a的值,即可得出答案.
14答案为:m>1.
【解析】
一次函数,当时,随的增大而减小.据此列式解答即可.
15【答案】 120
【解析】
设大套装的单价为元,小套装的单价为元,根据“购买2个小套装和购买1个大套装
共需220元;购买3个小套装和2个大套装,共需390元”,即可得出关于的二元一C方程组,解之即可得出结论.
16答案为:2.
三解答题(本大题共9题,共98分)
17(10分)【解析】
(1)根据算术平方根、立方根、乘方、绝对值的意义进行计算即可;
(2)根据二次根式的乘除法法则进行计算即可。
解:(1)
=
. 5分
(2),
,
10分
18(10分)【解析】
(1)利用加减消元法解方程组,由于两方程中的系数互为相反数,故应先用加减法求出的值,再用代入法求出的值.
(2)利用二元一次方程组解的意义,将 = 4代入方程中,求得值,再将值代入方程 =■中,计算即可得出结论.
解:(1)
①+②得,3x=3,
解得,x=1,
把x=1代入①得,1+3y=4,
解得,y=1,
故原方程组的解为; 5分
(2)将代入方程得:,
解得:,
将代入方程中,
,
即两个数为2和. 10分
19(10分)【解析】
先在△ABC中,由∠B=90°,可得△ABC为直角三角形;根据勾股定理得出,那么,由勾股定理的逆定理可得△ACD也为直角三角形.
解:都是直角三角形.理由如下:
连接AC.
在△ABC中,∵∠B=90°,
∴△ABC为直角三角形;
∴AC2=AB2+BC2=8, 5分
又∵AD2+AC2=1+8=9,而DC2=9,
∴AC2+AD2=DC2,
∴△ACD也为直角三角形 .10
20(10分)【解析】
(1)分析题意,根据点A、B的坐标,求出AB的长,再求出AB边上的高即可求出△ABC的面积;
(2)点A,B,C分别向上平移1个单位长度,再向右平移2个单位长度得到点,,,
,结合点的平移规律即可求出点,,三点的坐标.
解:(1),,,
,
中边上的高为,
. 5分
【2】画出三角形如图所示,
三角形先向上平移个单位长度,再向右平移个单位长度,得到三角形,
点,,分别向上平移个单位长度,再向右平移个单位长度,得到点,,,
,,.
10分
21(10分)【解析】
(1)由于应是的一次函数,根据表格数据利用待定系数法即可求解;
(2)利用(1)的函数关系式代入计算即可求解.
(1)解:依题意设y=kx+b,
则 ,
解得 ,
∴y= x+ ; 5分
(2)解:当x=39时,y= ×39+ ≠72.8,
故一把高39cm的椅子和一张高为72.8cm的课桌不配套
10分
22(12分)【解析】
(1)设商场购进甲种节能灯只,购进乙种节能灯只,正确列出二元一次方程组求解即可
(2)根据每只节能灯的利润,列出式子计算即可。
解:(1)设商场购进甲种节能灯只,购进乙种节能灯只,
根据题意得:, 4分
解得:.
答:商场购进甲种节能灯40只,购进乙种节能灯60只. 8分
(2)
(元.
答:商场共计获利1300元.
12分
23(12分)【解析】
(1)利用中位数的定义以及众数的定义分别求出即可;
(2)首先求出平均数进而利用方差公式得出即可;
(3)先求出乙队的方差,再利用方差的意义进而得出即可,
解:(1)答案为:9.5,10; 4分
(2)甲队的平均成绩和方差;=×(7+8+9+7+10+10+9+10+10+10)=9,
=×[(7﹣9)2+(8﹣9)2+(7﹣9)2+…+(10﹣10)2]
=(4+1+4+0+1+1+0+1+1+1)
=1.4 ; 8分
(3)乙队的平均成绩是:×(10×4+8×2+7+9×3)=9,
则方差是:×[4×(10﹣9)2+2×(8﹣9)2+(7﹣9)2+3×(9﹣9)2]=1.
∵乙队方差小于甲队方差,
∴乙队成绩较为整齐.
12分
24(12分)【解析】
过点P作MN∥AB,根据两直线平行,内错角相等,求出∠B=∠BPN, 可得MN∥CD,∠D=∠DPN, 可得∠BPD=∠B+∠D成立.
解:(2)∠BPD=∠B+∠D. 2分
证明:如图b,过点P作MN∥AB. 4分
∴∠B=∠BPN.
又∵AB∥CD,
∴MN∥CD. 8分
∴∠D=∠DPN.
∴∠BPD=∠BPN+∠DPN=∠B+∠D.
故∠BPD≠∠B﹣∠D,∠BPD=∠B+∠D. 12分
25【解析】
(1)利用待定系数法求直线解析式即可;
(2)联立两直线解析式即可求出交点坐标;
(3)先求出△ABO的面积,再根据△APC的面积是△ABO的面积的2倍,可得AC的长度,进一步可得点C
坐标.
解:(1)设直线的表达式为.
由点,的坐标分别为,,
可知
解得
所以直线的表达式为. 4分
【2】
由题意,
得
解得
所以点的坐标为. 8分
【3】
点,的坐标分别为,,,,
,,
△ABO的面积为,
△APC的面积是 的面积的倍,
△APC的面积为,
点坐标为,
,
解得,
点坐标为或.
12分
八年级 数学
题号 一选择题 二填空题 17 18 19 20 21 22 23 24 25
得分
评卷人
亲爱的同学,希望你沉着、冷静、诚信地迎接学期质量监测、相信你一定能考出理想
的成绩!
一选择题(每小题 3 分,共 36 分.每小题均有 A.B.C.D 四个选项,其中只有一个选项正确,
,请用 2B铅笔在答题卡相应位置填涂)
1. -8的立方根是( )
A. 2 B. -2 C. ±2 D. -4
2 下列每组数表示三条线段长,其中可以构成直角三角形的一组线段是( )
A. 1,2,3 B. 2,3,4 C. 3,4,5 D. 4,5,6
3.在平面直角坐标系中,点P(﹣3,5)关于x轴的对称点在( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
4.下列y关于x的函数关系式:① y=x;②y= ;③y= -1;④y= -x+10其中一次函数的个数是( )
A.4 B.3 C.2 D.1
5.刘翔在出征北京奥运会前刻苦进行110米跨栏训练,教练对他20次的训练成绩进行统计分析,判断他的成绩是否稳定,则教练需要知道刘翔这20次成绩的( )
A.众数 B.平均数 C.频数 D.方差
6 小丽在用“加减消元法”解二元一次方程组时,利用消去,则、的值可能是( )
A. , B. , C. , D. ,
7.如图,将直尺与含30°角的三角尺摆放在一起,若∠1=20°,则∠2的度数是( )
A.30° B.40° C.50° D.60°
8 若,则等于( )
A. 1 B. 5 C. D.
9. 小张参加了某公司的招聘考试,考试分面试和笔试(成绩均按百分制),面试占60%,笔试占40%,小张的面试和笔试成绩分别为92分和90分,则小张的综合成绩为( ).
A 91.2分 B 92分 C 90 分 D 91 分
10 已知 a,b满足方程组 ,则 a+b的值为( )
A. 2 B. 3 C. 4 D. 5
11.如图,直线l1:y=2x+1与直线l2:y=mx+n相交于点P(1,b),则关于x,y的方程组的解为( )
A. B. C. D.
12 如图,在平面直角坐标系中,一动点从原点O出发,按向上、向右、向下、向右的方向不断地移动,每移动一个单位,得到点A1(0,1)、A2(1,1)、A3(1,0)、A4(2,0)…,那么点A2023的坐标为( )
A.(1011,0) B. (1011,1)
C. (2022,0) D. (2022,1)
二填空题(每小题4分,共16分)
13. 若点在y轴上,则点M的坐标是________.
14.已知一次函数,若y随x的增大而减小,那么m的取值范围是 .
15. 第24届冬季奥林匹克运动会将于2022年02月04日至2022年02月20日在中华人民共和国北京市和张家口市联合举行,这是中国历史上第一次举办冬季奥运会冬奥会吉祥物“冰墩墩”和“雪容融”陶制品分为小套装和大套装两种已知购买2个小套装和购买1个大套装,共需220元;购买3个小套装和2个大套装,共需390元,则大套装的单价为____________元
16.如图,已知圆柱体底面圆的半径为,高为2,AB、CD分别是两底面的直径,AD,BC是母线.若一只蚂蚁从A点出发,从侧面爬行到C点,则蚂蚁爬行的最短路线的长度是 .(结果保留根式)
三解答题(本大题共9题,共98分,解答应写出必要的文字说明、证明过程或演算步骤)
17. (10分)计算:(1).
(2);
18 (10分)解下列方程组
(2)小明求得方程组的解为,由于不小心,滴上了墨水,刚好遮住了两个数和,求这两个数.
19 (10分)有一块薄铁皮ABCD,∠B=90°,各边的尺寸如图所示,若沿对角线AC剪开,得到的两块都是“直角三角形”形状吗?为什么?
20 (10分)如图,在平面直角坐标系中,三角形的顶点坐标分别为,,.
(1)求三角形的面积;
(2)如果将三角形先向上平移个单位长度,再向右平移个单位长度,得到三角形,画出三角形,并写出三角形'的各顶点坐标.
21.(10分)为保护学生视力,课桌椅的高度都是按一定的关系配套设计的,研究表明:假设课桌的高度为,椅子的高度为,则应是 的一次函数,下表列出两套符合条件的课桌椅的高度:
第一套 第二套
椅子高度 40 37
桌子高度 75 70
(1)请确定与的函数关系式;
(2)现有一把高39的椅子和一张高为72.8的课桌,它们是否配套?为什么?
22. (12分)为了响应市委和市政府“绿色环保,节能减排”的号召,幸福商场用3300元购进甲、乙两种节能灯共计100只,很快售完.这两种节能灯的进价、售价如下表:
进价(元只) 售价(元只)
甲种节能灯 30 40
乙种节能灯 35 50
(1)求幸福商场甲、乙两种节能灯各购进了多少只?
(2)全部售完100只节能灯后,商场共计获利多少元?
23. (12分)八(1)班组织了一次经典朗读比赛,甲、乙两队各10人的比赛成绩如下表
甲 7 8 9 7 10 10 9 10 10 10
乙 10 8 7 9 8 10 10 9 10 9
(1)甲队成绩的中位数是 分,乙队成绩的众数是 分;
(2)计算甲队的平均成绩和方差;
(3)成绩较为整齐的是哪个队?
24.(12分)平面内的两条直线有相交和平行两种位置关系.
(1)AB平行于CD.如图a,点P在AB,CD的外部时,由AB∥CD,有∠B=∠BOD,又因∠BOD是△POD的外角,故∠BOD=∠BPD+∠D,故∠BPD=∠B﹣∠D.
(2)如图b,将点P移到AB,CD的内部,以上结论是否成立?若不成立,则∠BPD,∠B,∠D之间有何数量关系?请证明你的结论;
25. (12分)如图,直线表达式为,点,的坐标分别为,,直线与直线相交于点.
(1)求直线的表达式:
(2)求点的坐标;
(3)若在轴上存在一点,使得的面积是的面积的倍,请直接写出点的坐标.
八年级 数学
参考答案
一选择题(每小题 3 分,共 36 分
1【答案】B
【解析】
根据立方根的定义直接得到答案
2【答案】C
【解析】根据勾股定理的逆定理,只有 中,能构成直角三角形,,故选
3【答案】C
【解析】直接利用关于轴对称点的性质得出答案。
4【答案】C
【解析】① y=x是正比例函数,是特殊的一次函数;
②y= 属于二次函数;
③y= -1不属于一次函数
④y= -x+10是一次函数。
综上所述,一次函数的个数是2个。故选:
5【答案】D
【解析】
众数 、平均数是反映一组数据的集中趋势,而频数是数据出现的次数,只有方差是反映数据的波动大小的。故为了判断成绩的稳定,需要知道的是方差。故选D
6【答案】D
【解析】为了消去,应使的系数互为相反数,由题意可知D正确
7【答案】C
【解析】
先根据三角形外角的性质,再根据平行线的性质得到∠2的度数.
8【答案】A
【解析】
根据二次根式有意义的条件得= 2,从而求得=—3,进而解决此题.
9【答案】A
【解析】
根据加权平均数的定义列式计算即可,
10【答案】C
【解析】
两式相加得 3a+3b-12,系数化为 1 即可解得.
11【答案】C
【解析】
首先利用y = 2x+ 1得到P点坐标,再根据两函数图象的交点坐标就是两函数组成的二元一次方程组的解可得答案.
12【答案】A
二填空题(每小题4分,共16分)
13【答案】
【解析】
直接利用y轴上点的坐标特点求出a的值,即可得出答案.
14答案为:m>1.
【解析】
一次函数,当时,随的增大而减小.据此列式解答即可.
15【答案】 120
【解析】
设大套装的单价为元,小套装的单价为元,根据“购买2个小套装和购买1个大套装
共需220元;购买3个小套装和2个大套装,共需390元”,即可得出关于的二元一C方程组,解之即可得出结论.
16答案为:2.
三解答题(本大题共9题,共98分)
17(10分)【解析】
(1)根据算术平方根、立方根、乘方、绝对值的意义进行计算即可;
(2)根据二次根式的乘除法法则进行计算即可。
解:(1)
=
. 5分
(2),
,
10分
18(10分)【解析】
(1)利用加减消元法解方程组,由于两方程中的系数互为相反数,故应先用加减法求出的值,再用代入法求出的值.
(2)利用二元一次方程组解的意义,将 = 4代入方程中,求得值,再将值代入方程 =■中,计算即可得出结论.
解:(1)
①+②得,3x=3,
解得,x=1,
把x=1代入①得,1+3y=4,
解得,y=1,
故原方程组的解为; 5分
(2)将代入方程得:,
解得:,
将代入方程中,
,
即两个数为2和. 10分
19(10分)【解析】
先在△ABC中,由∠B=90°,可得△ABC为直角三角形;根据勾股定理得出,那么,由勾股定理的逆定理可得△ACD也为直角三角形.
解:都是直角三角形.理由如下:
连接AC.
在△ABC中,∵∠B=90°,
∴△ABC为直角三角形;
∴AC2=AB2+BC2=8, 5分
又∵AD2+AC2=1+8=9,而DC2=9,
∴AC2+AD2=DC2,
∴△ACD也为直角三角形 .10
20(10分)【解析】
(1)分析题意,根据点A、B的坐标,求出AB的长,再求出AB边上的高即可求出△ABC的面积;
(2)点A,B,C分别向上平移1个单位长度,再向右平移2个单位长度得到点,,,
,结合点的平移规律即可求出点,,三点的坐标.
解:(1),,,
,
中边上的高为,
. 5分
【2】画出三角形如图所示,
三角形先向上平移个单位长度,再向右平移个单位长度,得到三角形,
点,,分别向上平移个单位长度,再向右平移个单位长度,得到点,,,
,,.
10分
21(10分)【解析】
(1)由于应是的一次函数,根据表格数据利用待定系数法即可求解;
(2)利用(1)的函数关系式代入计算即可求解.
(1)解:依题意设y=kx+b,
则 ,
解得 ,
∴y= x+ ; 5分
(2)解:当x=39时,y= ×39+ ≠72.8,
故一把高39cm的椅子和一张高为72.8cm的课桌不配套
10分
22(12分)【解析】
(1)设商场购进甲种节能灯只,购进乙种节能灯只,正确列出二元一次方程组求解即可
(2)根据每只节能灯的利润,列出式子计算即可。
解:(1)设商场购进甲种节能灯只,购进乙种节能灯只,
根据题意得:, 4分
解得:.
答:商场购进甲种节能灯40只,购进乙种节能灯60只. 8分
(2)
(元.
答:商场共计获利1300元.
12分
23(12分)【解析】
(1)利用中位数的定义以及众数的定义分别求出即可;
(2)首先求出平均数进而利用方差公式得出即可;
(3)先求出乙队的方差,再利用方差的意义进而得出即可,
解:(1)答案为:9.5,10; 4分
(2)甲队的平均成绩和方差;=×(7+8+9+7+10+10+9+10+10+10)=9,
=×[(7﹣9)2+(8﹣9)2+(7﹣9)2+…+(10﹣10)2]
=(4+1+4+0+1+1+0+1+1+1)
=1.4 ; 8分
(3)乙队的平均成绩是:×(10×4+8×2+7+9×3)=9,
则方差是:×[4×(10﹣9)2+2×(8﹣9)2+(7﹣9)2+3×(9﹣9)2]=1.
∵乙队方差小于甲队方差,
∴乙队成绩较为整齐.
12分
24(12分)【解析】
过点P作MN∥AB,根据两直线平行,内错角相等,求出∠B=∠BPN, 可得MN∥CD,∠D=∠DPN, 可得∠BPD=∠B+∠D成立.
解:(2)∠BPD=∠B+∠D. 2分
证明:如图b,过点P作MN∥AB. 4分
∴∠B=∠BPN.
又∵AB∥CD,
∴MN∥CD. 8分
∴∠D=∠DPN.
∴∠BPD=∠BPN+∠DPN=∠B+∠D.
故∠BPD≠∠B﹣∠D,∠BPD=∠B+∠D. 12分
25【解析】
(1)利用待定系数法求直线解析式即可;
(2)联立两直线解析式即可求出交点坐标;
(3)先求出△ABO的面积,再根据△APC的面积是△ABO的面积的2倍,可得AC的长度,进一步可得点C
坐标.
解:(1)设直线的表达式为.
由点,的坐标分别为,,
可知
解得
所以直线的表达式为. 4分
【2】
由题意,
得
解得
所以点的坐标为. 8分
【3】
点,的坐标分别为,,,,
,,
△ABO的面积为,
△APC的面积是 的面积的倍,
△APC的面积为,
点坐标为,
,
解得,
点坐标为或.
12分
同课章节目录
