2.5.2 矩形的判定 课件(共30张PPT)
文档属性
| 名称 | 2.5.2 矩形的判定 课件(共30张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-01-25 00:00:00 | ||
图片预览



文档简介
(共30张PPT)
第一章 直角三角形
2.5.2矩形的判定
01
教学目标
02
新知导入
03
新知讲解
04
课堂练习
05
课堂小结
06
作业布置
01
教学目标
01
02
03
02
新知导入
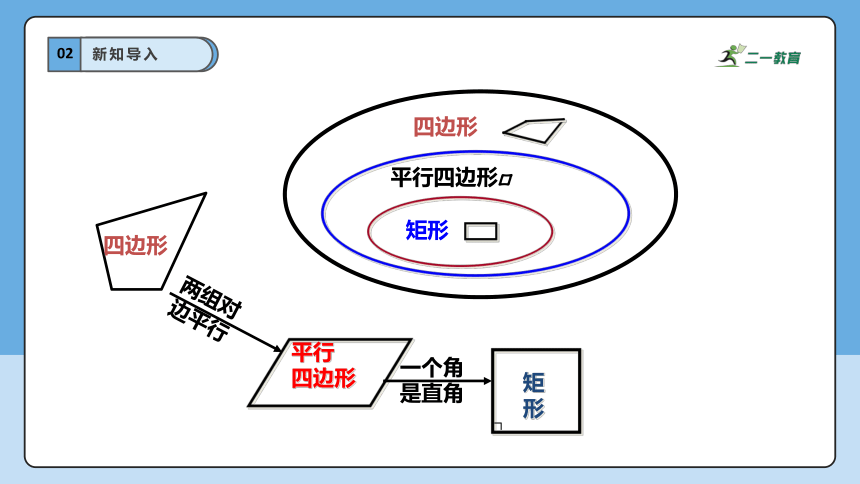
四边形
平行
四边形
两组对
边平行
一个角
是直角
∟
矩形
平行四边形□
矩形
四边形
03
新知探究
测量…?
木工朋友在制作窗框后,需要检测所制作的窗框是否是矩形,那么他需要测量哪些数据,其根据又是什么呢?
你现在有办法帮他吗
03
新知探究
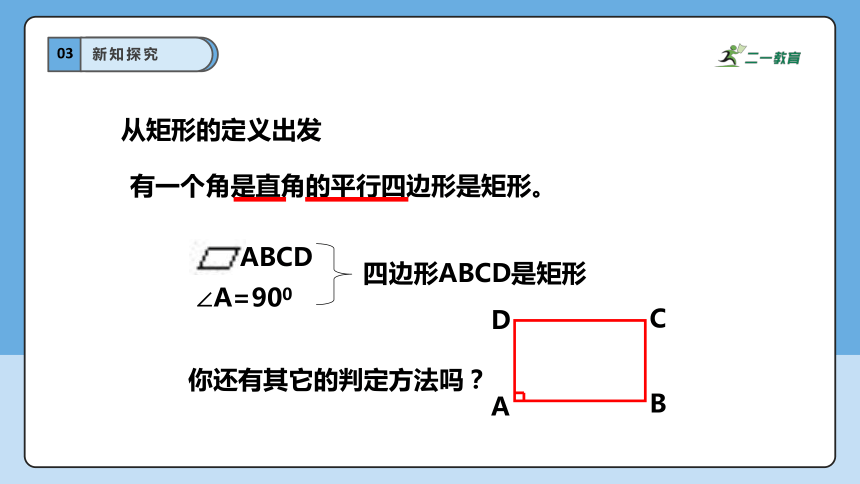
从矩形的定义出发
有一个角是直角的平行四边形是矩形。
你还有其它的判定方法吗?
ABCD
∠A=900
四边形ABCD是矩形
A
B
C
D
03
新知讲解
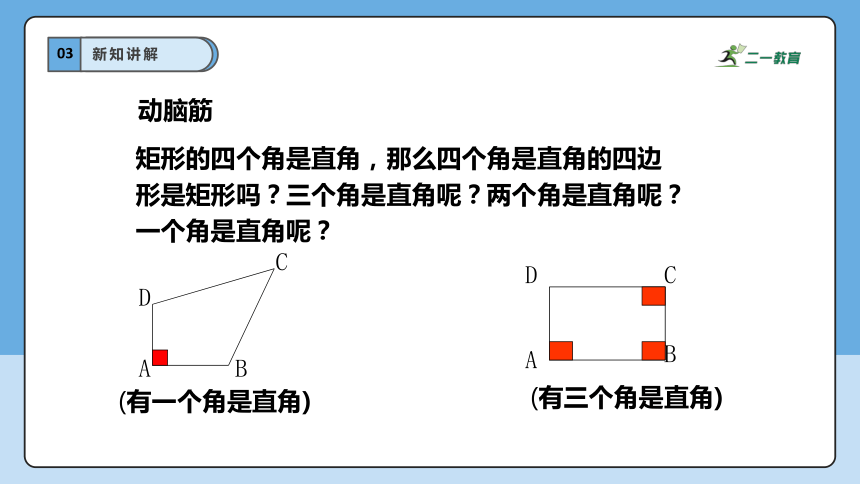
动脑筋
矩形的四个角是直角,那么四个角是直角的四边形是矩形吗?三个角是直角呢?两个角是直角呢?一个角是直角呢?
A
B
D
C
(有一个角是直角)
A
B
D
C
(有三个角是直角)
03
新知讲解
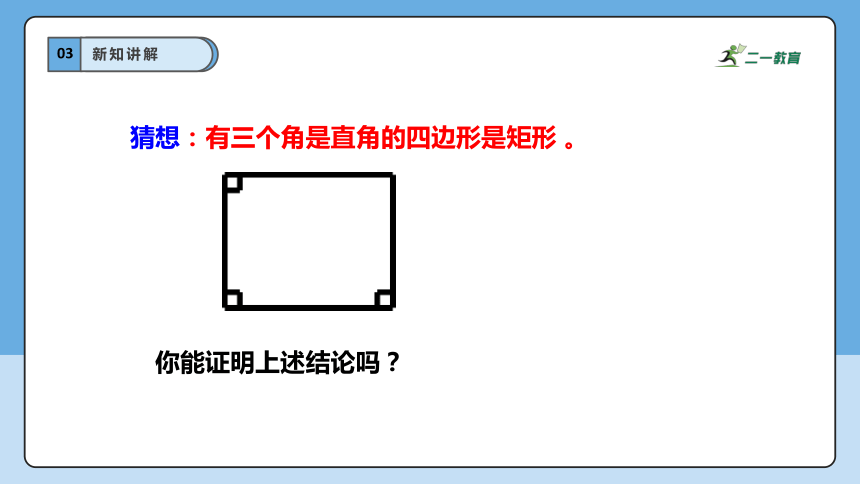
猜想:有三个角是直角的四边形是矩形 。
你能证明上述结论吗?
03
新知讲解
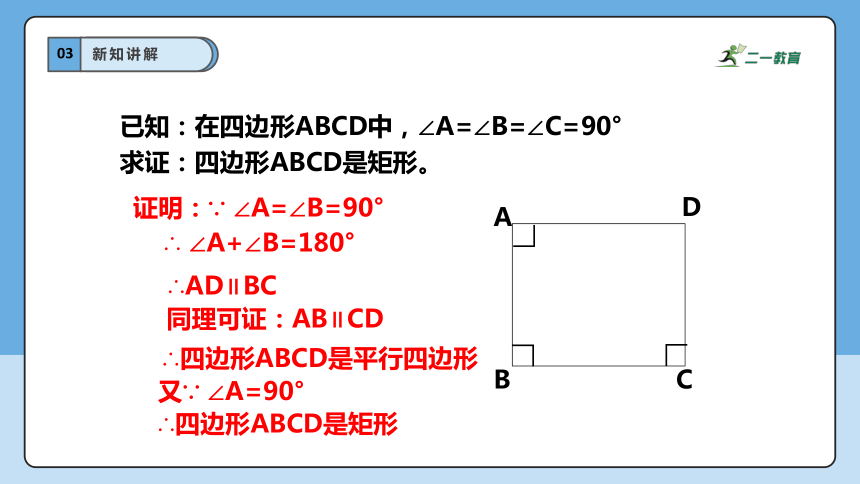
已知:在四边形ABCD中,∠A=∠B=∠C=90°
求证:四边形ABCD是矩形。
A
B
C
D
∟
∟
∟
证明:∵ ∠A=∠B=90°
∴ ∠A+∠B=180°
∴AD∥BC
同理可证:AB∥CD
∴四边形ABCD是平行四边形
又∵ ∠A=90°
∴四边形ABCD是矩形
03
新知讲解
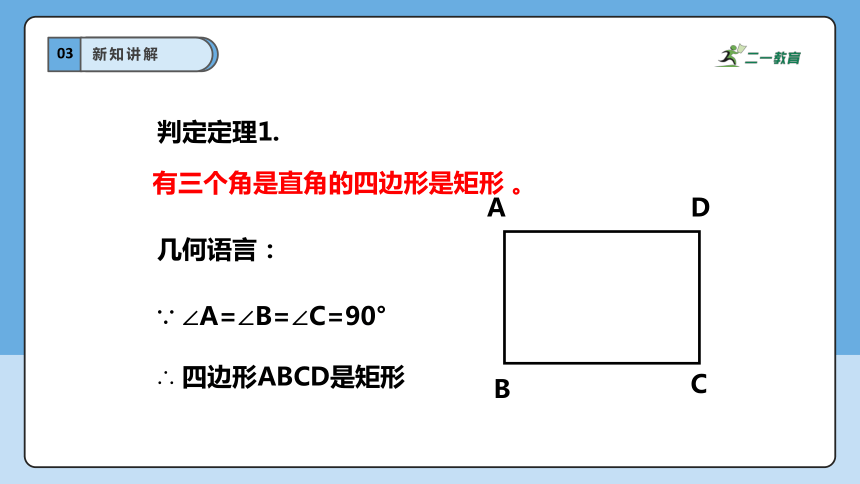
判定定理1.
有三个角是直角的四边形是矩形 。
A
B
C
D
∵ ∠A=∠B=∠C=90°
∴ 四边形ABCD是矩形
几何语言:
03
新知讲解
动脑筋
从“矩形的两条对角线相等且互相平分”这一性质受到启发,你能画出一个对角线长度是4cm的矩形吗?这样的矩形有多少个?
03
新知讲解
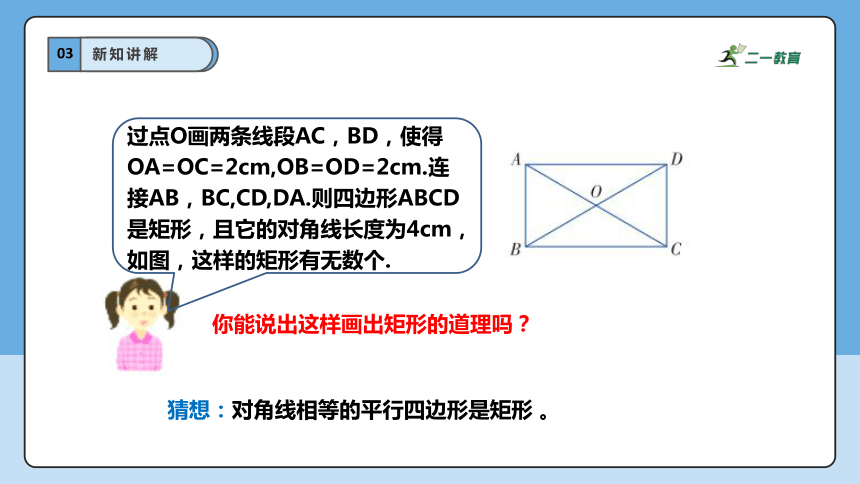
猜想:对角线相等的平行四边形是矩形 。
过点O画两条线段AC,BD,使得OA=OC=2cm,OB=OD=2cm.连接AB,BC,CD,DA.则四边形ABCD是矩形,且它的对角线长度为4cm,如图,这样的矩形有无数个.
你能说出这样画出矩形的道理吗?
03
新知讲解
已知:平行四边形ABCD,AC=BD。求证:四边形ABCD是矩形。
A
B
C
D
证明:
∵ AB=CD, BC=BC, AC=BD
∴ △ABC≌ △DCB(SSS)
∵ AB//CD
∴ ∠ABC+∠DCB=180°
∴ ∠ABC=∠DCB=90°
又∵ 四边形ABCD是平行四边形
∴四边形ABCD是矩形。
∴ ∠ABC=∠DCB
03
新知讲解
对角线相等的平行四边形是矩形 。
判定定理2.
几何语言:
∵四边形ABCD是平行四边形
AC=BD
∴四边形ABCD是矩形
A
B
C
D
O
(或OA=OC=OB=OD)
03
新知讲解
测量…?
现在你可以帮助木工朋友检测所制作的窗框是否是矩形了吧,你可以测量哪些数据,有几种方案,根据又是什么呢?
03
新知讲解
分别测量出两组对边的长度和一个内角的度数,如果两组对边的长度分别相等,且这个内角是直角,则窗框符合规格
方案一:
测量出三个内角的度数,如果三个内角都是直角,则窗框符合规格
方案二:
分别测量出窗框四边和两条对角线的长度,如果窗框两组对边长度、两条对角线的长度分别相等,那么窗框符合规格
方案三:
03
新知讲解
矩形的判定方法总结
有一个角是直角的平行四边形是矩形。
(对角线相等且互相平分的四边形是矩形。)
有三个角是直角的四边形是矩形 。
方法1:
方法2:
方法3:
对角线相等的平行四边形是矩形 。
03
新知讲解
议一议
对角线相等的四边形是矩形吗 举例说明.
等腰梯形
新课探究
例
如图,在□ ABCD 中,它的两条对角线相交于点O。
(1)如果□ ABCD是矩形,试问: △OBC是什么样的三角形?
(2)如果△OBC是等腰三角形,其中:OB=OC,那么□ABCD是矩形吗?
A
B
C
D
O
新课探究
解:(1)∵ □ ABCD是矩形,
∴AC与DB相等且互相平分
∴OB= AC=OC
∴ △OBC是等腰三角形.
(2)∵△OBC是等腰三角形,其中OB=OC
∴AC=2OC=2OB=BD
∴ □ ABCD是矩形
04
课堂练习
【知识技能类作业】必做题:
1.在数学活动课上,老师和同学们判断一个四边形门框是否为矩形,下面是某合作学习小组的4位同学拟定的方案,其中正确的是( )
A.测量对角线是否相互平分
B.测量两组对边是否分别相等
C.测量一组对角是否为直角
D.测量四边形的其中三个角是否都为直角
D
04
课堂练习
【知识技能类作业】选做题:
2.如图,在△ABC中,AB=AC,将△ABC绕点C旋转180°得到△FEC,连接AE,BF.当∠ACB为__________度时,四边形ABFE为矩形.
60
04
课堂练习
【综合拓展类作业】
3、如图,四边形ABCD是平行四边形,AC,BD交于点O,∠1=∠2.求证:四边形ABCD是矩形.
04
课堂练习
【综合拓展类作业】
证明:∵∠1=∠2,
∴BO=CO,即2BO=2CO.
∵四边形ABCD是平行四边形,
∴AO=CO,BO=OD.
∴AC=2CO,BD=2BO.
∴AC=BD.
∵四边形ABCD是平行四边形,
∴四边形ABCD是矩形.
05
课堂小结
∠A= ∠B= ∠C=90°
ABCD
AC = BD
ABCD
∠A=90°
ABCD
是矩形
四边形ABCD
是矩形
判定一个四边形是矩形的方法是:
06
作业布置
【知识技能类作业】必做题:
1.如图,要使平行四边形ABCD成为矩形,需添加的条件是( )
A.AB=BC B.AC⊥BD
C.AC=BD D.∠1=∠2
C
06
作业布置
【知识技能类作业】选做题:
2.如图△ABC中,AC的垂直平分线分别交AC,AB于点D,F,BE⊥DF交DF的延长线于点E,已∠A=30°,BC=2,AF=BF,则四边形BCDE的面积是 .
2
06
作业布置
【综合拓展类作业】
3.如图,直线EF∥MN,PQ交EF、MN于A、C两点,AB、CB、CD、AD分别是∠ EAC、 ∠ MCA、 ∠ ACN、 ∠ CAF的角平分线,则四边形ABCD是什么特殊多边形?
矩形
Thanks!
https://www.21cnjy.com/recruitment/home/fine
第一章 直角三角形
2.5.2矩形的判定
01
教学目标
02
新知导入
03
新知讲解
04
课堂练习
05
课堂小结
06
作业布置
01
教学目标
01
02
03
02
新知导入
四边形
平行
四边形
两组对
边平行
一个角
是直角
∟
矩形
平行四边形□
矩形
四边形
03
新知探究
测量…?
木工朋友在制作窗框后,需要检测所制作的窗框是否是矩形,那么他需要测量哪些数据,其根据又是什么呢?
你现在有办法帮他吗
03
新知探究
从矩形的定义出发
有一个角是直角的平行四边形是矩形。
你还有其它的判定方法吗?
ABCD
∠A=900
四边形ABCD是矩形
A
B
C
D
03
新知讲解
动脑筋
矩形的四个角是直角,那么四个角是直角的四边形是矩形吗?三个角是直角呢?两个角是直角呢?一个角是直角呢?
A
B
D
C
(有一个角是直角)
A
B
D
C
(有三个角是直角)
03
新知讲解
猜想:有三个角是直角的四边形是矩形 。
你能证明上述结论吗?
03
新知讲解
已知:在四边形ABCD中,∠A=∠B=∠C=90°
求证:四边形ABCD是矩形。
A
B
C
D
∟
∟
∟
证明:∵ ∠A=∠B=90°
∴ ∠A+∠B=180°
∴AD∥BC
同理可证:AB∥CD
∴四边形ABCD是平行四边形
又∵ ∠A=90°
∴四边形ABCD是矩形
03
新知讲解
判定定理1.
有三个角是直角的四边形是矩形 。
A
B
C
D
∵ ∠A=∠B=∠C=90°
∴ 四边形ABCD是矩形
几何语言:
03
新知讲解
动脑筋
从“矩形的两条对角线相等且互相平分”这一性质受到启发,你能画出一个对角线长度是4cm的矩形吗?这样的矩形有多少个?
03
新知讲解
猜想:对角线相等的平行四边形是矩形 。
过点O画两条线段AC,BD,使得OA=OC=2cm,OB=OD=2cm.连接AB,BC,CD,DA.则四边形ABCD是矩形,且它的对角线长度为4cm,如图,这样的矩形有无数个.
你能说出这样画出矩形的道理吗?
03
新知讲解
已知:平行四边形ABCD,AC=BD。求证:四边形ABCD是矩形。
A
B
C
D
证明:
∵ AB=CD, BC=BC, AC=BD
∴ △ABC≌ △DCB(SSS)
∵ AB//CD
∴ ∠ABC+∠DCB=180°
∴ ∠ABC=∠DCB=90°
又∵ 四边形ABCD是平行四边形
∴四边形ABCD是矩形。
∴ ∠ABC=∠DCB
03
新知讲解
对角线相等的平行四边形是矩形 。
判定定理2.
几何语言:
∵四边形ABCD是平行四边形
AC=BD
∴四边形ABCD是矩形
A
B
C
D
O
(或OA=OC=OB=OD)
03
新知讲解
测量…?
现在你可以帮助木工朋友检测所制作的窗框是否是矩形了吧,你可以测量哪些数据,有几种方案,根据又是什么呢?
03
新知讲解
分别测量出两组对边的长度和一个内角的度数,如果两组对边的长度分别相等,且这个内角是直角,则窗框符合规格
方案一:
测量出三个内角的度数,如果三个内角都是直角,则窗框符合规格
方案二:
分别测量出窗框四边和两条对角线的长度,如果窗框两组对边长度、两条对角线的长度分别相等,那么窗框符合规格
方案三:
03
新知讲解
矩形的判定方法总结
有一个角是直角的平行四边形是矩形。
(对角线相等且互相平分的四边形是矩形。)
有三个角是直角的四边形是矩形 。
方法1:
方法2:
方法3:
对角线相等的平行四边形是矩形 。
03
新知讲解
议一议
对角线相等的四边形是矩形吗 举例说明.
等腰梯形
新课探究
例
如图,在□ ABCD 中,它的两条对角线相交于点O。
(1)如果□ ABCD是矩形,试问: △OBC是什么样的三角形?
(2)如果△OBC是等腰三角形,其中:OB=OC,那么□ABCD是矩形吗?
A
B
C
D
O
新课探究
解:(1)∵ □ ABCD是矩形,
∴AC与DB相等且互相平分
∴OB= AC=OC
∴ △OBC是等腰三角形.
(2)∵△OBC是等腰三角形,其中OB=OC
∴AC=2OC=2OB=BD
∴ □ ABCD是矩形
04
课堂练习
【知识技能类作业】必做题:
1.在数学活动课上,老师和同学们判断一个四边形门框是否为矩形,下面是某合作学习小组的4位同学拟定的方案,其中正确的是( )
A.测量对角线是否相互平分
B.测量两组对边是否分别相等
C.测量一组对角是否为直角
D.测量四边形的其中三个角是否都为直角
D
04
课堂练习
【知识技能类作业】选做题:
2.如图,在△ABC中,AB=AC,将△ABC绕点C旋转180°得到△FEC,连接AE,BF.当∠ACB为__________度时,四边形ABFE为矩形.
60
04
课堂练习
【综合拓展类作业】
3、如图,四边形ABCD是平行四边形,AC,BD交于点O,∠1=∠2.求证:四边形ABCD是矩形.
04
课堂练习
【综合拓展类作业】
证明:∵∠1=∠2,
∴BO=CO,即2BO=2CO.
∵四边形ABCD是平行四边形,
∴AO=CO,BO=OD.
∴AC=2CO,BD=2BO.
∴AC=BD.
∵四边形ABCD是平行四边形,
∴四边形ABCD是矩形.
05
课堂小结
∠A= ∠B= ∠C=90°
ABCD
AC = BD
ABCD
∠A=90°
ABCD
是矩形
四边形ABCD
是矩形
判定一个四边形是矩形的方法是:
06
作业布置
【知识技能类作业】必做题:
1.如图,要使平行四边形ABCD成为矩形,需添加的条件是( )
A.AB=BC B.AC⊥BD
C.AC=BD D.∠1=∠2
C
06
作业布置
【知识技能类作业】选做题:
2.如图△ABC中,AC的垂直平分线分别交AC,AB于点D,F,BE⊥DF交DF的延长线于点E,已∠A=30°,BC=2,AF=BF,则四边形BCDE的面积是 .
2
06
作业布置
【综合拓展类作业】
3.如图,直线EF∥MN,PQ交EF、MN于A、C两点,AB、CB、CD、AD分别是∠ EAC、 ∠ MCA、 ∠ ACN、 ∠ CAF的角平分线,则四边形ABCD是什么特殊多边形?
矩形
Thanks!
https://www.21cnjy.com/recruitment/home/fine
同课章节目录
- 第1章 直角三角形
- 1.1 直角三角形的性质与判定(Ⅰ)
- 1.2 直角三角形的性质与判定(Ⅱ)
- 1.3 直角三角形全等的判定
- 1.4 角平分线的性质
- 第2章 四边形
- 2.1 多边形
- 2.2 平行四边形
- 2.3 中心对称和中心对称图形
- 2.4 三角形的中位线
- 2.5 矩形
- 2.6 菱形
- 2.7 正方形
- 第3章 图形与坐标
- 3.1 平面直角坐标系
- 3.2 简单图形的坐标表示
- 3.3 轴对称和平移的坐标表示
- 第4章 一次函数
- 4.1 函数和它的表示法
- 4.2 一次函数
- 4.3 一次函数的图象
- 4.4 用待定系数法确定一次函数表达式
- 4.5 一次函数的应用
- 第5章 数据的频数分布
- 5.1 频数与频率
- 5.2 频数直方图
