人教版(2024版)七下数学 7.2.3 平行线的性质(第一课时)同步练习(含解析)
文档属性
| 名称 | 人教版(2024版)七下数学 7.2.3 平行线的性质(第一课时)同步练习(含解析) |  | |
| 格式 | zip | ||
| 文件大小 | 899.1KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-01-25 14:59:36 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
7.2.3 平行线的性质(第一课时) 同步练习
班级:________ 姓名:________
一、单选题
1.如图,直线,和是直线被直线所截形成的角,若,则( )
A. B. C. D.
2.如图,,若,则的度数是( )
A. B. C. D.
3.如图,直线被直线所截,已知,则的度数为( )
A. B. C. D.
4.当光线从空气射入水中时,光线的传播方向发生了改变(如图所示),这就是光的折射现象.图中,则的度数为( )
A. B. C. D.
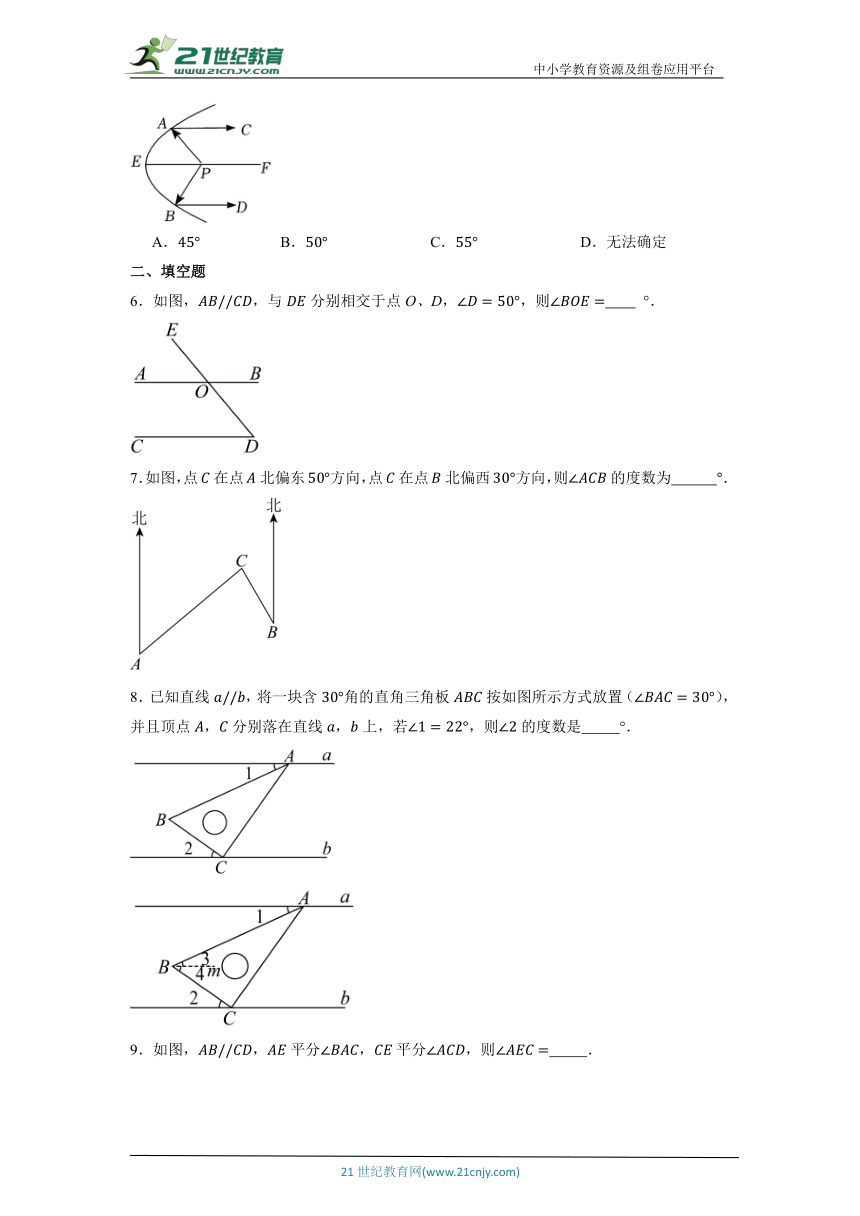
5.生活中常见的探照灯、汽车大灯等灯具都与抛物线有关.如图,从光源P点照射到抛物线上的光线,等反射以后沿着与平行的方向射出,若,,则的度数为( )
A. B. C. D.无法确定
二、填空题
6.如图,,与分别相交于点O、D,,则 °.
7.如图,点在点北偏东方向,点在点北偏西方向,则的度数为 .
8.已知直线,将一块含角的直角三角板按如图所示方式放置(),并且顶点,分别落在直线,上,若,则的度数是 °.
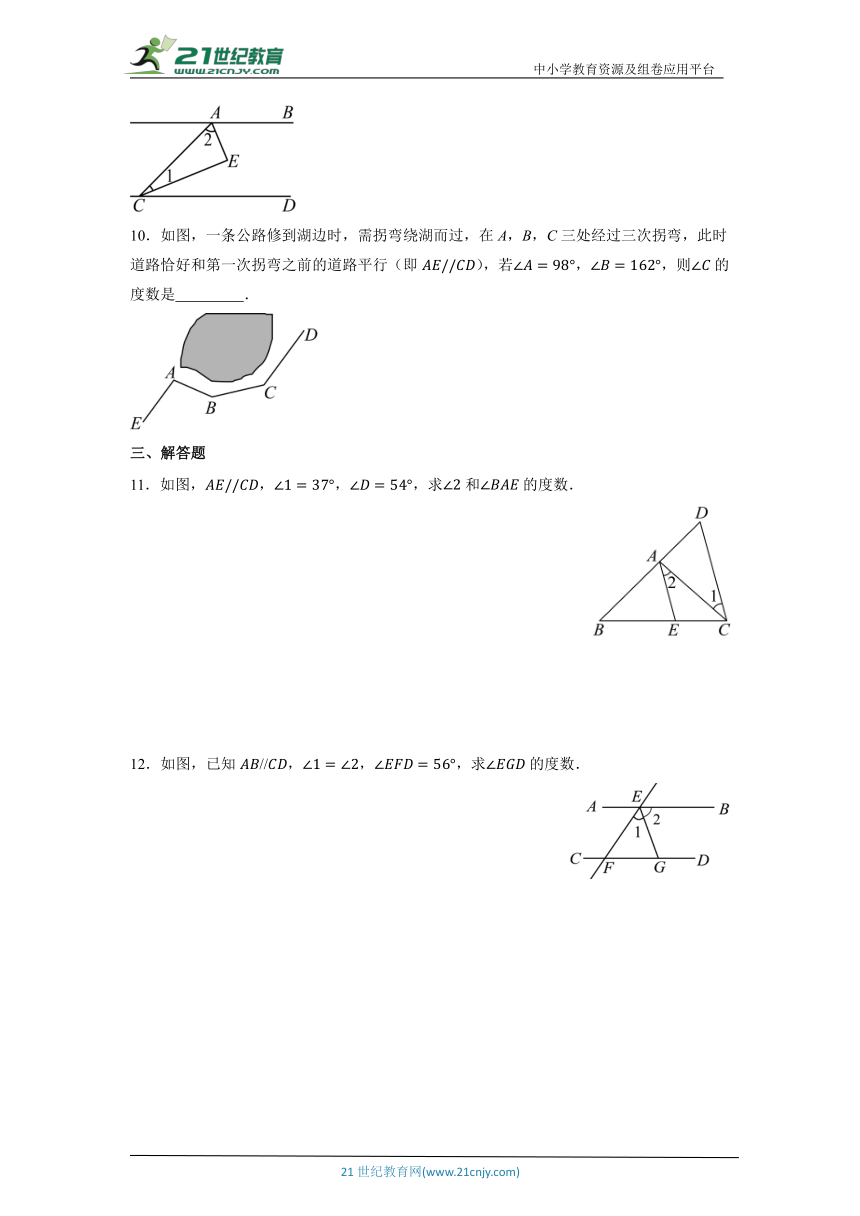
9.如图,,平分,平分,则 .
10.如图,一条公路修到湖边时,需拐弯绕湖而过,在A,B,C三处经过三次拐弯,此时道路恰好和第一次拐弯之前的道路平行(即),若,,则的度数是 .
三、解答题
11.如图,,求和的度数.
12.如图,已知,,,求的度数.
答案与解析
7.2.3 平行线的性质(第一课时) 同步练习
班级:________ 姓名:________
一、单选题
1.如图,直线,和是直线被直线所截形成的角,若,则( )
A. B. C. D.
【答案】B
【解析】本题考查了平行线的性质,根据两直线平行同位角相等即可求解.
解:∵,
∴
故选:B.
2.如图,,若,则的度数是( )
A. B. C. D.
【答案】D
【解析】本题主要考查了平行线的性质以及对顶角相等的运用,解决问题的关键是掌握:两直线平行,同旁内角互补.
根据两直线平行,同旁内角互补和对顶角相等解答.
解:,
,
,
,
故选:D.
3.如图,直线被直线所截,已知,则的度数为( )
A. B. C. D.
【答案】B
【解析】本题考查了平行线的性质,邻补角,根据平行线的性质可得,进而根据邻补角的定义,即可求解.
解:如图所示
∵,
∴
∴,
故选:B.
4.当光线从空气射入水中时,光线的传播方向发生了改变(如图所示),这就是光的折射现象.图中,则的度数为( )
A. B. C. D.
【答案】C
【解析】本题考查了平行线的性质,熟记平行线的性质定理是解题的关键.根据“两直线平行,内错角相等”求解即可.
解:如图,
,
,
,
,
故选:C.
5.生活中常见的探照灯、汽车大灯等灯具都与抛物线有关.如图,从光源P点照射到抛物线上的光线,等反射以后沿着与平行的方向射出,若,,则的度数为( )
A. B. C. D.无法确定
【答案】C
【解析】本题主要考查了平行线的性质,根据两直线平行,内错角相等可得,又因为,所以,再根据,即可解得.
解:∵,,
∴,
∵,
∴,
∵,
∴.
故选:C.
二、填空题
6.如图,,与分别相交于点O、D,,则 °.
【答案】130
【解析】本题考查了平行线的性质,邻补角,先根据平行线的性质求出,然后根据邻补角的定义求解即可.
解:∵,,
∴,
∴.
故答案为:130.
7.如图,点在点北偏东方向,点在点北偏西方向,则的度数为 .
【答案】
【解析】本题考查了方向角,平行线的判定和性质,过点作,可得,即得,,再根据角的和差即可求解,正确作出辅助线是解题的关键.
解:过点作,
∵,
∴,
∴,,
∴,
故答案为:.
8.已知直线,将一块含角的直角三角板按如图所示方式放置(),并且顶点,分别落在直线,上,若,则的度数是 °.
【答案】38
【解析】本题考查了平行线的判定和性质,两直线平行,内错角相等.作,根据平行线的性质求得,,再结合三角板的角的度数即可求得答案.
解:作,
∵,
∴,
∴,,
∵,
∴,
∴,
∴,
∴,
故答案为:38.
9.如图,,平分,平分,则 .
【答案】
【解析】本题考查了平行公理推论、平行线的性质、角平分线的定义,熟练掌握平行线的性质是解题关键.过点作,先根据平行线的性质可得,,再根据角平分线的定义可得,,从而可得,然后根据角的和差、等量代换求解即可得.
解:如图,过点作,
∴,
∵,,
∴,
∴,
∵平分,平分,
∴,,
又∵,
∴,
∴,
∴,
故答案为:.
10.如图,一条公路修到湖边时,需拐弯绕湖而过,在A,B,C三处经过三次拐弯,此时道路恰好和第一次拐弯之前的道路平行(即),若,,则的度数是 .
【答案】
【解析】本题考查了平行公理推论、平行线的性质,熟练掌握平行线的性质是解题关键.过点作,先根据平行线的性质可得,从而可得,再根据平行公理推论可得,根据平行线的性质求解即可得.
解:如图,过点作,
∴,
∵,
∴,
由题意可知,,
∴,
∴,
故答案为:.
三、解答题
11.如图,,求和的度数.
【答案】,
【解析】根据平行线的性质进行求解即可.
解:∵,
∴(两直线平行,内错角相等)
∴(两直线平行,同位角相等)
12.如图,已知,,,求的度数.
【答案】
【解析】本题考查了平行线性质.根据平行以及的度数,可求得的度数,进而根据求得的度数,再根据平行线性质求出.
解:,,
;
,
;
,
.
21世纪教育网(www.21cnjy.com)
7.2.3 平行线的性质(第一课时) 同步练习
班级:________ 姓名:________
一、单选题
1.如图,直线,和是直线被直线所截形成的角,若,则( )
A. B. C. D.
2.如图,,若,则的度数是( )
A. B. C. D.
3.如图,直线被直线所截,已知,则的度数为( )
A. B. C. D.
4.当光线从空气射入水中时,光线的传播方向发生了改变(如图所示),这就是光的折射现象.图中,则的度数为( )
A. B. C. D.
5.生活中常见的探照灯、汽车大灯等灯具都与抛物线有关.如图,从光源P点照射到抛物线上的光线,等反射以后沿着与平行的方向射出,若,,则的度数为( )
A. B. C. D.无法确定
二、填空题
6.如图,,与分别相交于点O、D,,则 °.
7.如图,点在点北偏东方向,点在点北偏西方向,则的度数为 .
8.已知直线,将一块含角的直角三角板按如图所示方式放置(),并且顶点,分别落在直线,上,若,则的度数是 °.
9.如图,,平分,平分,则 .
10.如图,一条公路修到湖边时,需拐弯绕湖而过,在A,B,C三处经过三次拐弯,此时道路恰好和第一次拐弯之前的道路平行(即),若,,则的度数是 .
三、解答题
11.如图,,求和的度数.
12.如图,已知,,,求的度数.
答案与解析
7.2.3 平行线的性质(第一课时) 同步练习
班级:________ 姓名:________
一、单选题
1.如图,直线,和是直线被直线所截形成的角,若,则( )
A. B. C. D.
【答案】B
【解析】本题考查了平行线的性质,根据两直线平行同位角相等即可求解.
解:∵,
∴
故选:B.
2.如图,,若,则的度数是( )
A. B. C. D.
【答案】D
【解析】本题主要考查了平行线的性质以及对顶角相等的运用,解决问题的关键是掌握:两直线平行,同旁内角互补.
根据两直线平行,同旁内角互补和对顶角相等解答.
解:,
,
,
,
故选:D.
3.如图,直线被直线所截,已知,则的度数为( )
A. B. C. D.
【答案】B
【解析】本题考查了平行线的性质,邻补角,根据平行线的性质可得,进而根据邻补角的定义,即可求解.
解:如图所示
∵,
∴
∴,
故选:B.
4.当光线从空气射入水中时,光线的传播方向发生了改变(如图所示),这就是光的折射现象.图中,则的度数为( )
A. B. C. D.
【答案】C
【解析】本题考查了平行线的性质,熟记平行线的性质定理是解题的关键.根据“两直线平行,内错角相等”求解即可.
解:如图,
,
,
,
,
故选:C.
5.生活中常见的探照灯、汽车大灯等灯具都与抛物线有关.如图,从光源P点照射到抛物线上的光线,等反射以后沿着与平行的方向射出,若,,则的度数为( )
A. B. C. D.无法确定
【答案】C
【解析】本题主要考查了平行线的性质,根据两直线平行,内错角相等可得,又因为,所以,再根据,即可解得.
解:∵,,
∴,
∵,
∴,
∵,
∴.
故选:C.
二、填空题
6.如图,,与分别相交于点O、D,,则 °.
【答案】130
【解析】本题考查了平行线的性质,邻补角,先根据平行线的性质求出,然后根据邻补角的定义求解即可.
解:∵,,
∴,
∴.
故答案为:130.
7.如图,点在点北偏东方向,点在点北偏西方向,则的度数为 .
【答案】
【解析】本题考查了方向角,平行线的判定和性质,过点作,可得,即得,,再根据角的和差即可求解,正确作出辅助线是解题的关键.
解:过点作,
∵,
∴,
∴,,
∴,
故答案为:.
8.已知直线,将一块含角的直角三角板按如图所示方式放置(),并且顶点,分别落在直线,上,若,则的度数是 °.
【答案】38
【解析】本题考查了平行线的判定和性质,两直线平行,内错角相等.作,根据平行线的性质求得,,再结合三角板的角的度数即可求得答案.
解:作,
∵,
∴,
∴,,
∵,
∴,
∴,
∴,
∴,
故答案为:38.
9.如图,,平分,平分,则 .
【答案】
【解析】本题考查了平行公理推论、平行线的性质、角平分线的定义,熟练掌握平行线的性质是解题关键.过点作,先根据平行线的性质可得,,再根据角平分线的定义可得,,从而可得,然后根据角的和差、等量代换求解即可得.
解:如图,过点作,
∴,
∵,,
∴,
∴,
∵平分,平分,
∴,,
又∵,
∴,
∴,
∴,
故答案为:.
10.如图,一条公路修到湖边时,需拐弯绕湖而过,在A,B,C三处经过三次拐弯,此时道路恰好和第一次拐弯之前的道路平行(即),若,,则的度数是 .
【答案】
【解析】本题考查了平行公理推论、平行线的性质,熟练掌握平行线的性质是解题关键.过点作,先根据平行线的性质可得,从而可得,再根据平行公理推论可得,根据平行线的性质求解即可得.
解:如图,过点作,
∴,
∵,
∴,
由题意可知,,
∴,
∴,
故答案为:.
三、解答题
11.如图,,求和的度数.
【答案】,
【解析】根据平行线的性质进行求解即可.
解:∵,
∴(两直线平行,内错角相等)
∴(两直线平行,同位角相等)
12.如图,已知,,,求的度数.
【答案】
【解析】本题考查了平行线性质.根据平行以及的度数,可求得的度数,进而根据求得的度数,再根据平行线性质求出.
解:,,
;
,
;
,
.
21世纪教育网(www.21cnjy.com)
同课章节目录
