2024-2025年北师大版数学八年级下册1.3线段的垂直平分线(1)课堂达标测试(含答案)
文档属性
| 名称 | 2024-2025年北师大版数学八年级下册1.3线段的垂直平分线(1)课堂达标测试(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 168.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-01-26 09:09:32 | ||
图片预览


文档简介
第一章《三角形的证明》3 线段的垂直平分线(1)
2025年北师大版数学八(下)课堂达标测试
一、选择题(每题5分,共25分)
1.如图,在 中, 的垂直平分线交 于点D, 平分 ,若 ,则 的度数为( )
A. B. C. D.
2.如图, 的垂直平分线 交 于点D,若 ,则 的度数是( )
A.25° B.20° C.30° D.15°
3.如图,等边三角形ABC中,AD⊥BC,垂足为D,点E在线段AD上,∠EBC=45°,则∠ACE等于( )
A.15° B.30° C.45° D.60°
4.如图,等腰△ABC的底边BC长为6,面积是36,腰AC的垂直平分线EF分别交AC,AB边于E,F点.若点D为BC边的中点,点M为线段EF上一动点,则△CDM周长的最小值为( )
A.6 B.10 C.15 D.16
5.如图,在中,分别为边上的高,相交于点,,连接,则下列结论:①;②;③;④若,则周长等于的长.其中正确的有( )
A.①② B.①③ C.①③④ D.②③④
二、填空题(每题5分,共25分)
6.如图,△ABC的边AB的垂直平分线交AC于点D,连接BD.若AC=8,CD=5,则BD= .
7.如图,在 中, 是 的垂直平分线.若 , 的周长为13,则 的周长为 .
8.如图,在△ABC中,AB=5,AC=7,直线DE垂直平分BC,垂足为E,交AC于点D,则△ABD的周长是 .
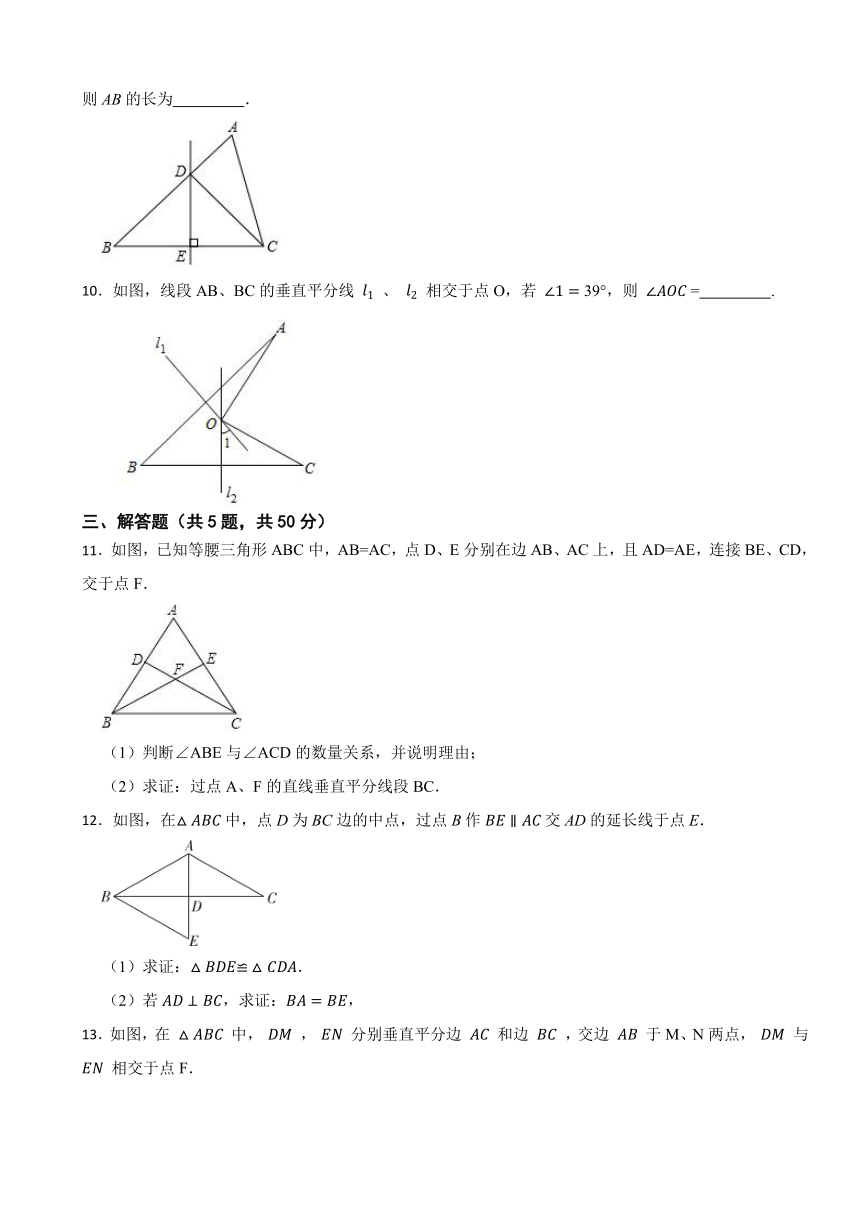
9.如图,在△ABC中,AC=4,∠A=60°,∠B=45°,BC边的垂直平分线DE交AB于点D,连接CD,则AB的长为 .
10.如图,线段AB、BC的垂直平分线 、 相交于点O,若 39°,则 = .
三、解答题(共5题,共50分)
11.如图,已知等腰三角形ABC中,AB=AC,点D、E分别在边AB、AC上,且AD=AE,连接BE、CD,交于点F.
(1)判断∠ABE与∠ACD的数量关系,并说明理由;
(2)求证:过点A、F的直线垂直平分线段BC.
12.如图,在中,点D为BC边的中点,过点B作交AD的延长线于点E.
(1)求证:.
(2)若,求证:,
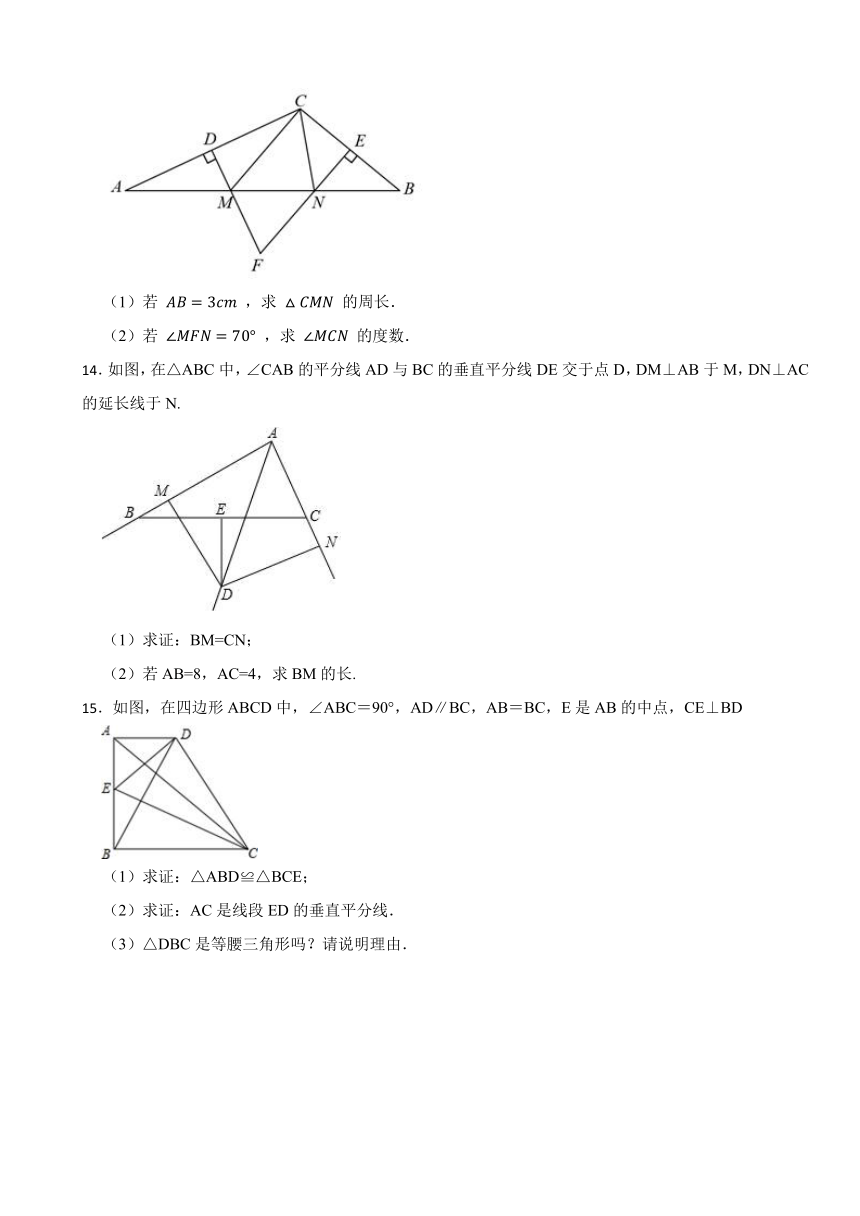
13.如图,在 中, , 分别垂直平分边 和边 ,交边 于M、N两点, 与 相交于点F.
(1)若 ,求 的周长.
(2)若 ,求 的度数.
14.如图,在△ABC中,∠CAB的平分线AD与BC的垂直平分线DE交于点D,DM⊥AB于M,DN⊥AC的延长线于N.
(1)求证:BM=CN;
(2)若AB=8,AC=4,求BM的长.
15.如图,在四边形ABCD中,∠ABC=90°,AD∥BC,AB=BC,E是AB的中点,CE⊥BD
(1)求证:△ABD≌△BCE;
(2)求证:AC是线段ED的垂直平分线.
(3)△DBC是等腰三角形吗?请说明理由.
答案解析部分
1.【答案】B
2.【答案】D
3.【答案】A
4.【答案】C
5.【答案】C
6.【答案】3
7.【答案】19
8.【答案】12
9.【答案】2+2
10.【答案】78°
11.【答案】(1)解:∠ABE=∠ACD;
在△ABE和△ACD中,
,
∴△ABE≌△ACD,
∴∠ABE=∠ACD;
(2)证明:∵AB=AC,
∴∠ABC=∠ACB,
由(1)可知∠ABE=∠ACD,
∴∠FBC=∠FCB,
∴FB=FC,
∵AB=AC,
∴点A、F均在线段BC的垂直平分线上,
即直线AF垂直平分线段BC.
12.【答案】(1)证明:为BC的中点,
.
.
在和中,
.
(2)证明:,
∴
垂直平分AE,
.
13.【答案】(1)解: 、 分别垂直平分 和 ,
, ,
的周长 ;
(2)解: ,
,
, ,
,
,
, ,
, ,
.
14.【答案】(1)证明:连接BD、CD,如图所示:
∵AD是∠CAB的平分线,DM⊥AB,DN⊥AC,
∴DM=DN,
∵DE垂直平分线BC,
∴DB=DC,
在Rt△DMB和Rt△DNC中,
∴Rt△DMB≌Rt△DNC(HL),
∴BM=CN;
(2)解:由(1)得:BM=CN,
∵AD是∠CAB的平分线,DM⊥AB,DN⊥AC,
∴DM=DN,
在Rt△DMA和Rt△DNA中,
∴Rt△DMA≌Rt△DNA(HL),
∴AM=AN,
∵AM=AB-BM,AN=AC+CN,
∴AB-BM=AC+CN,
∴2BM=AB-AC=8-4=4,
∴BM=2.
15.【答案】(1)解:如图证明:∵∠ABC=90°,BD⊥EC,
∴∠1+∠3=90°,∠2+∠3=90°,
∴∠1=∠2,
在△BAD和△CBE中,
,
∴△BAD≌△CBE(ASA),
(2)证明:∵E是AB中点,
∴EB=EA,
∵AD=BE,
∴AE=AD,
∵AD∥BC,
∴∠7=∠ACB=45°,
∵∠6=45°,
∴∠6=∠7,
又∵AD=AE,
∴AM⊥DE,且EM=DM,
即AC是线段ED的垂直平分线;
(3)解:△DBC是等腰三角形(CD=BD).
理由如下:
∵由(2)得:CD=CE,由(1)得:CE=BD,
∴CD=BD.
∴△DBC是等腰三角形.
2025年北师大版数学八(下)课堂达标测试
一、选择题(每题5分,共25分)
1.如图,在 中, 的垂直平分线交 于点D, 平分 ,若 ,则 的度数为( )
A. B. C. D.
2.如图, 的垂直平分线 交 于点D,若 ,则 的度数是( )
A.25° B.20° C.30° D.15°
3.如图,等边三角形ABC中,AD⊥BC,垂足为D,点E在线段AD上,∠EBC=45°,则∠ACE等于( )
A.15° B.30° C.45° D.60°
4.如图,等腰△ABC的底边BC长为6,面积是36,腰AC的垂直平分线EF分别交AC,AB边于E,F点.若点D为BC边的中点,点M为线段EF上一动点,则△CDM周长的最小值为( )
A.6 B.10 C.15 D.16
5.如图,在中,分别为边上的高,相交于点,,连接,则下列结论:①;②;③;④若,则周长等于的长.其中正确的有( )
A.①② B.①③ C.①③④ D.②③④
二、填空题(每题5分,共25分)
6.如图,△ABC的边AB的垂直平分线交AC于点D,连接BD.若AC=8,CD=5,则BD= .
7.如图,在 中, 是 的垂直平分线.若 , 的周长为13,则 的周长为 .
8.如图,在△ABC中,AB=5,AC=7,直线DE垂直平分BC,垂足为E,交AC于点D,则△ABD的周长是 .
9.如图,在△ABC中,AC=4,∠A=60°,∠B=45°,BC边的垂直平分线DE交AB于点D,连接CD,则AB的长为 .
10.如图,线段AB、BC的垂直平分线 、 相交于点O,若 39°,则 = .
三、解答题(共5题,共50分)
11.如图,已知等腰三角形ABC中,AB=AC,点D、E分别在边AB、AC上,且AD=AE,连接BE、CD,交于点F.
(1)判断∠ABE与∠ACD的数量关系,并说明理由;
(2)求证:过点A、F的直线垂直平分线段BC.
12.如图,在中,点D为BC边的中点,过点B作交AD的延长线于点E.
(1)求证:.
(2)若,求证:,
13.如图,在 中, , 分别垂直平分边 和边 ,交边 于M、N两点, 与 相交于点F.
(1)若 ,求 的周长.
(2)若 ,求 的度数.
14.如图,在△ABC中,∠CAB的平分线AD与BC的垂直平分线DE交于点D,DM⊥AB于M,DN⊥AC的延长线于N.
(1)求证:BM=CN;
(2)若AB=8,AC=4,求BM的长.
15.如图,在四边形ABCD中,∠ABC=90°,AD∥BC,AB=BC,E是AB的中点,CE⊥BD
(1)求证:△ABD≌△BCE;
(2)求证:AC是线段ED的垂直平分线.
(3)△DBC是等腰三角形吗?请说明理由.
答案解析部分
1.【答案】B
2.【答案】D
3.【答案】A
4.【答案】C
5.【答案】C
6.【答案】3
7.【答案】19
8.【答案】12
9.【答案】2+2
10.【答案】78°
11.【答案】(1)解:∠ABE=∠ACD;
在△ABE和△ACD中,
,
∴△ABE≌△ACD,
∴∠ABE=∠ACD;
(2)证明:∵AB=AC,
∴∠ABC=∠ACB,
由(1)可知∠ABE=∠ACD,
∴∠FBC=∠FCB,
∴FB=FC,
∵AB=AC,
∴点A、F均在线段BC的垂直平分线上,
即直线AF垂直平分线段BC.
12.【答案】(1)证明:为BC的中点,
.
.
在和中,
.
(2)证明:,
∴
垂直平分AE,
.
13.【答案】(1)解: 、 分别垂直平分 和 ,
, ,
的周长 ;
(2)解: ,
,
, ,
,
,
, ,
, ,
.
14.【答案】(1)证明:连接BD、CD,如图所示:
∵AD是∠CAB的平分线,DM⊥AB,DN⊥AC,
∴DM=DN,
∵DE垂直平分线BC,
∴DB=DC,
在Rt△DMB和Rt△DNC中,
∴Rt△DMB≌Rt△DNC(HL),
∴BM=CN;
(2)解:由(1)得:BM=CN,
∵AD是∠CAB的平分线,DM⊥AB,DN⊥AC,
∴DM=DN,
在Rt△DMA和Rt△DNA中,
∴Rt△DMA≌Rt△DNA(HL),
∴AM=AN,
∵AM=AB-BM,AN=AC+CN,
∴AB-BM=AC+CN,
∴2BM=AB-AC=8-4=4,
∴BM=2.
15.【答案】(1)解:如图证明:∵∠ABC=90°,BD⊥EC,
∴∠1+∠3=90°,∠2+∠3=90°,
∴∠1=∠2,
在△BAD和△CBE中,
,
∴△BAD≌△CBE(ASA),
(2)证明:∵E是AB中点,
∴EB=EA,
∵AD=BE,
∴AE=AD,
∵AD∥BC,
∴∠7=∠ACB=45°,
∵∠6=45°,
∴∠6=∠7,
又∵AD=AE,
∴AM⊥DE,且EM=DM,
即AC是线段ED的垂直平分线;
(3)解:△DBC是等腰三角形(CD=BD).
理由如下:
∵由(2)得:CD=CE,由(1)得:CE=BD,
∴CD=BD.
∴△DBC是等腰三角形.
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
