2024-2025学年苏科版数学七年级下册第8章整式乘法同步分层练习(含简单答案)
文档属性
| 名称 | 2024-2025学年苏科版数学七年级下册第8章整式乘法同步分层练习(含简单答案) |  | |
| 格式 | docx | ||
| 文件大小 | 341.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-01-26 09:21:39 | ||
图片预览




文档简介
2024-2025学年苏科版数学七年级下册
第8章整式乘法
(同步分层练习)
(满分100分,时间90分钟)
选择题(本题共8小题,每题3分,共24分)
1.下列式子中,计算结果为的是
A. B. C. D.
2.计算的结果是
A. B.
C. D.
3. 下列各式不能用平方差公式计算的是( )
A. B. C. D.
4.如果等式成立,那么m和n的值分别是( )
A., B., C., D.,
5.若,则常数k的值是( )
A. 2 B. 4 C. 1 D.
6.已知,代数式的值是( )
A. 2 B. C. 4 D.
7.某小区有一正方形草坪如图所示,小区物业现对该草坪进行改造,将该正方形草坪边方向的长度增加3米,边方向的长度减少3米,则改造后的长方形草坪面积与原来正方形草坪面积相比( )
A. 增加6平方米 B. 增加9平方米 C. 减少9平方米 D. 保持不变
8.如图,大正方形与小正方形面积之差为S,则图中阴影部分的面积是( )
A. B. S C. D.
填空题(本题共8小题,每题3分,共24分)
9.______.
10.已知是一个完全平方式,则m的值为______.
11.若a-b=1,ab=-2,则(a+1)(b-1)=_______.
12.已知,则的值为__________________________.
已知,,则______.
14.已知 ,则 的值为___________.
15.是完全平方式,与的乘积中不含x的一次项,则的值为______.
16. 如图①所示,长为、宽为(,均为定值,且)的小长方形纸片,现将张这样的小长方形纸片按如图②所示的方式不重叠地放在长方形内,未被覆盖的部分(两个长方形)用阴影表示.设左上角的阴影部分的面积为,右下角的阴影部分的面积为,记,当的长度变化时,按照同样的放置方式,此时的值始终保持不变,则,应满足的关系式是______.(用含n的代数式表示m)
三、解答题(本题共8小题,共52分)
17.计算:
(1)
(2)
(3).
18.先化简,再求值:,其中,.
19.已知求下列各式的值;
(1);
(2).
20.已知展开的结果中,不含和项.(,为常数)
(1)求,的值;
(2)在()的条件下,求的值.
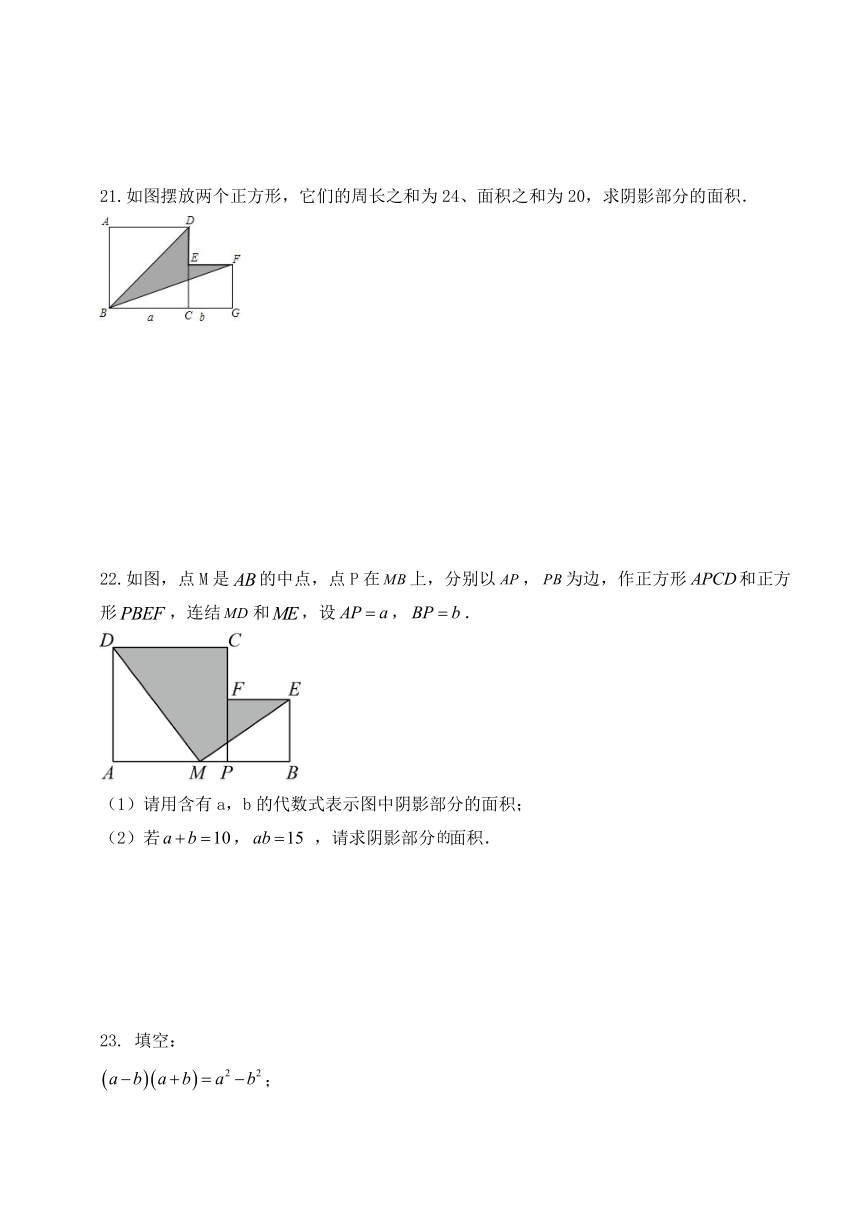
21.如图摆放两个正方形,它们的周长之和为24、面积之和为20,求阴影部分的面积.
22.如图,点M是的中点,点P在上,分别以,为边,作正方形和正方形,连结和,设,.
(1)请用含有a,b的代数式表示图中阴影部分的面积;
(2)若, ,请求阴影部分面积.
23. 填空:
;
;
;
…
(1)______;
(2)猜想:
______;(其中为正整数,且)
(3)利用(2)中的猜想的结论计算:
①
②.
24.我们定义:一个整数能表示成(a、b是整数)形式,则称这个数为“完美数”.
例如,5是“完美数”.理由:因为,所以5是“完美数”.
[解决问题]
(1)已知29是“完美数”,请将它写成(a、b是整数)的形式______;
(2)若可配方成(m、n为常数),则______;
[探究问题]
(3)已知,则______;
(4)已知(x、y是整数,k是常数),要使S为“完美数”,试求出符合条件的一个k值,并说明理由.
[拓展结论]
(5)已知实数x、y满足,求的最值.
答案解析
一、选择题(本题共8小题,每题3分,共24分)
1.下列式子中,计算结果为的是
A. B. C. D.
【答案】C
2.计算的结果是
A. B.
C. D.
【答案】C
3. 下列各式不能用平方差公式计算的是( )
A. B. C. D.
【答案】C
4.如果等式成立,那么m和n的值分别是( )
A., B., C., D.,
【答案】B
5.若,则常数k的值是( )
A. 2 B. 4 C. 1 D.
【答案】B
6.已知,代数式的值是( )
A. 2 B. C. 4 D.
【答案】D
7.某小区有一正方形草坪如图所示,小区物业现对该草坪进行改造,将该正方形草坪边方向的长度增加3米,边方向的长度减少3米,则改造后的长方形草坪面积与原来正方形草坪面积相比( )
A. 增加6平方米 B. 增加9平方米 C. 减少9平方米 D. 保持不变
【答案】C
8.如图,大正方形与小正方形面积之差为S,则图中阴影部分的面积是( )
A. B. S C. D.
【答案】C
二、填空题(本题共8小题,每题3分,共24分)
9.______.
【答案】
10.已知是一个完全平方式,则m的值为______.
【答案】16
11.若a-b=1,ab=-2,则(a+1)(b-1)=_______.
【答案】-4.
12.已知,则的值为__________________________.
【答案】1
已知,,则______.
【答案】17
14.已知 ,则 的值为___________.
【答案】
15.是完全平方式,与的乘积中不含x的一次项,则的值为______.
【答案】或
16. 如图①所示,长为、宽为(,均为定值,且)的小长方形纸片,现将张这样的小长方形纸片按如图②所示的方式不重叠地放在长方形内,未被覆盖的部分(两个长方形)用阴影表示.设左上角的阴影部分的面积为,右下角的阴影部分的面积为,记,当的长度变化时,按照同样的放置方式,此时的值始终保持不变,则,应满足的关系式是______.(用含n的代数式表示m)
【答案】3n
三、解答题(本题共8小题,共52分)
17.计算:
(1)
(2)
(3).
【答案】(1)
(2)
(3)
18.先化简,再求值:,其中,.
【答案】,
19.已知求下列各式的值;
(1);
(2).
【答案】(1)
(2)
20.已知展开的结果中,不含和项.(,为常数)
(1)求,的值;
(2)在()的条件下,求的值.
【答案】(1),;
(2),.
21.如图摆放两个正方形,它们的周长之和为24、面积之和为20,求阴影部分的面积.
【答案】(由题意得,
∴ a+b=6,
∴ ,
即 ,
∴ab=8,
∴
=6
22.如图,点M是的中点,点P在上,分别以,为边,作正方形和正方形,连结和,设,.
(1)请用含有a,b的代数式表示图中阴影部分的面积;
(2)若, ,请求阴影部分面积.
【答案】(1);
(2)45.
23. 填空:
;
;
;
…
(1)______;
(2)猜想:
______;(其中为正整数,且)
(3)利用(2)中的猜想的结论计算:
①
②.
【答案】(1)
(2)
(3)①,②
24.我们定义:一个整数能表示成(a、b是整数)形式,则称这个数为“完美数”.
例如,5是“完美数”.理由:因为,所以5是“完美数”.
[解决问题]
(1)已知29是“完美数”,请将它写成(a、b是整数)的形式______;
(2)若可配方成(m、n为常数),则______;
[探究问题]
(3)已知,则______;
(4)已知(x、y是整数,k是常数),要使S为“完美数”,试求出符合条件的一个k值,并说明理由.
[拓展结论]
(5)已知实数x、y满足,求的最值.
【答案】(1);
(2)
(3)
(4)
(5)最大值为:;
第8章整式乘法
(同步分层练习)
(满分100分,时间90分钟)
选择题(本题共8小题,每题3分,共24分)
1.下列式子中,计算结果为的是
A. B. C. D.
2.计算的结果是
A. B.
C. D.
3. 下列各式不能用平方差公式计算的是( )
A. B. C. D.
4.如果等式成立,那么m和n的值分别是( )
A., B., C., D.,
5.若,则常数k的值是( )
A. 2 B. 4 C. 1 D.
6.已知,代数式的值是( )
A. 2 B. C. 4 D.
7.某小区有一正方形草坪如图所示,小区物业现对该草坪进行改造,将该正方形草坪边方向的长度增加3米,边方向的长度减少3米,则改造后的长方形草坪面积与原来正方形草坪面积相比( )
A. 增加6平方米 B. 增加9平方米 C. 减少9平方米 D. 保持不变
8.如图,大正方形与小正方形面积之差为S,则图中阴影部分的面积是( )
A. B. S C. D.
填空题(本题共8小题,每题3分,共24分)
9.______.
10.已知是一个完全平方式,则m的值为______.
11.若a-b=1,ab=-2,则(a+1)(b-1)=_______.
12.已知,则的值为__________________________.
已知,,则______.
14.已知 ,则 的值为___________.
15.是完全平方式,与的乘积中不含x的一次项,则的值为______.
16. 如图①所示,长为、宽为(,均为定值,且)的小长方形纸片,现将张这样的小长方形纸片按如图②所示的方式不重叠地放在长方形内,未被覆盖的部分(两个长方形)用阴影表示.设左上角的阴影部分的面积为,右下角的阴影部分的面积为,记,当的长度变化时,按照同样的放置方式,此时的值始终保持不变,则,应满足的关系式是______.(用含n的代数式表示m)
三、解答题(本题共8小题,共52分)
17.计算:
(1)
(2)
(3).
18.先化简,再求值:,其中,.
19.已知求下列各式的值;
(1);
(2).
20.已知展开的结果中,不含和项.(,为常数)
(1)求,的值;
(2)在()的条件下,求的值.
21.如图摆放两个正方形,它们的周长之和为24、面积之和为20,求阴影部分的面积.
22.如图,点M是的中点,点P在上,分别以,为边,作正方形和正方形,连结和,设,.
(1)请用含有a,b的代数式表示图中阴影部分的面积;
(2)若, ,请求阴影部分面积.
23. 填空:
;
;
;
…
(1)______;
(2)猜想:
______;(其中为正整数,且)
(3)利用(2)中的猜想的结论计算:
①
②.
24.我们定义:一个整数能表示成(a、b是整数)形式,则称这个数为“完美数”.
例如,5是“完美数”.理由:因为,所以5是“完美数”.
[解决问题]
(1)已知29是“完美数”,请将它写成(a、b是整数)的形式______;
(2)若可配方成(m、n为常数),则______;
[探究问题]
(3)已知,则______;
(4)已知(x、y是整数,k是常数),要使S为“完美数”,试求出符合条件的一个k值,并说明理由.
[拓展结论]
(5)已知实数x、y满足,求的最值.
答案解析
一、选择题(本题共8小题,每题3分,共24分)
1.下列式子中,计算结果为的是
A. B. C. D.
【答案】C
2.计算的结果是
A. B.
C. D.
【答案】C
3. 下列各式不能用平方差公式计算的是( )
A. B. C. D.
【答案】C
4.如果等式成立,那么m和n的值分别是( )
A., B., C., D.,
【答案】B
5.若,则常数k的值是( )
A. 2 B. 4 C. 1 D.
【答案】B
6.已知,代数式的值是( )
A. 2 B. C. 4 D.
【答案】D
7.某小区有一正方形草坪如图所示,小区物业现对该草坪进行改造,将该正方形草坪边方向的长度增加3米,边方向的长度减少3米,则改造后的长方形草坪面积与原来正方形草坪面积相比( )
A. 增加6平方米 B. 增加9平方米 C. 减少9平方米 D. 保持不变
【答案】C
8.如图,大正方形与小正方形面积之差为S,则图中阴影部分的面积是( )
A. B. S C. D.
【答案】C
二、填空题(本题共8小题,每题3分,共24分)
9.______.
【答案】
10.已知是一个完全平方式,则m的值为______.
【答案】16
11.若a-b=1,ab=-2,则(a+1)(b-1)=_______.
【答案】-4.
12.已知,则的值为__________________________.
【答案】1
已知,,则______.
【答案】17
14.已知 ,则 的值为___________.
【答案】
15.是完全平方式,与的乘积中不含x的一次项,则的值为______.
【答案】或
16. 如图①所示,长为、宽为(,均为定值,且)的小长方形纸片,现将张这样的小长方形纸片按如图②所示的方式不重叠地放在长方形内,未被覆盖的部分(两个长方形)用阴影表示.设左上角的阴影部分的面积为,右下角的阴影部分的面积为,记,当的长度变化时,按照同样的放置方式,此时的值始终保持不变,则,应满足的关系式是______.(用含n的代数式表示m)
【答案】3n
三、解答题(本题共8小题,共52分)
17.计算:
(1)
(2)
(3).
【答案】(1)
(2)
(3)
18.先化简,再求值:,其中,.
【答案】,
19.已知求下列各式的值;
(1);
(2).
【答案】(1)
(2)
20.已知展开的结果中,不含和项.(,为常数)
(1)求,的值;
(2)在()的条件下,求的值.
【答案】(1),;
(2),.
21.如图摆放两个正方形,它们的周长之和为24、面积之和为20,求阴影部分的面积.
【答案】(由题意得,
∴ a+b=6,
∴ ,
即 ,
∴ab=8,
∴
=6
22.如图,点M是的中点,点P在上,分别以,为边,作正方形和正方形,连结和,设,.
(1)请用含有a,b的代数式表示图中阴影部分的面积;
(2)若, ,请求阴影部分面积.
【答案】(1);
(2)45.
23. 填空:
;
;
;
…
(1)______;
(2)猜想:
______;(其中为正整数,且)
(3)利用(2)中的猜想的结论计算:
①
②.
【答案】(1)
(2)
(3)①,②
24.我们定义:一个整数能表示成(a、b是整数)形式,则称这个数为“完美数”.
例如,5是“完美数”.理由:因为,所以5是“完美数”.
[解决问题]
(1)已知29是“完美数”,请将它写成(a、b是整数)的形式______;
(2)若可配方成(m、n为常数),则______;
[探究问题]
(3)已知,则______;
(4)已知(x、y是整数,k是常数),要使S为“完美数”,试求出符合条件的一个k值,并说明理由.
[拓展结论]
(5)已知实数x、y满足,求的最值.
【答案】(1);
(2)
(3)
(4)
(5)最大值为:;
同课章节目录
- 第7章 平面图形的认识(二)
- 7.1 探索直线平行的条件
- 7.2 探索平行线的性质
- 7.3 图形的平移
- 7.4 认识三角形
- 7.5 多边形的内角和与外角和
- 第8章 幂的运算
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 第9章 整式乘法与因式分解
- 9.1 单项式乘单项式
- 9.2 单项式乘多项式
- 9.3 多项式乘多项式
- 9.4 乘法公式
- 9.5 多项式的因式分解
- 第10章 二元一次方程组
- 10.1 二元一次方程
- 10.2 二元一次方程组
- 10.3 解二元一次方程组
- 10.4 三元一次方程组
- 10.5 用二元一次方程解决问题
- 第11章 一元一次不等式
- 11.1 生活中的不等式
- 11.2 不等式的解集
- 11.3 不等式的性质
- 11.4 解一元一次不等式
- 11.5 用一元一次不等式解决问题
- 11.6 一元一次不等式组
- 第12章 证明
- 12.1 定义与命题
- 12.2 证明
- 12.3 互逆命题
