北师版数学九下 1.4 解直角三角形 课件(共28张PPT)
文档属性
| 名称 | 北师版数学九下 1.4 解直角三角形 课件(共28张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-01-27 11:26:21 | ||
图片预览








文档简介
(共28张PPT)
第一章 直角三角形的边角关系 1.4
解直角三角形
北师大版九年级下册数学课件
目录
目录
CONTENTS
CONTENTS
1-新知导入
2-探究新知
3-巩固练习
4-课堂小结
新知导入
第一部分
PART 01
your content is entered here, or by copying your text, select paste in this box and choose to retain only text. your content is typed here
A
C
B
c
b
a
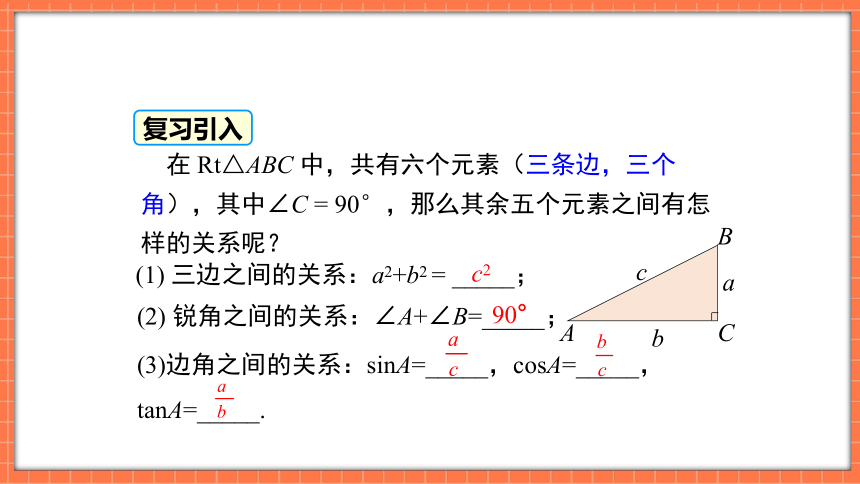
(1) 三边之间的关系:a2+b2 = _____;
(2) 锐角之间的关系:∠A+∠B=_____;
(3)边角之间的关系:sinA=_____,cosA=_____,
tanA=_____.
在 Rt△ABC 中,共有六个元素(三条边,三个角),其中∠C = 90°,那么其余五个元素之间有怎样的关系呢?
c2
90°
复习引入
问题1 如果已知 Rt△ABC 中两边的长,你能求出这个三角形其他的元素吗?
已知两边解直角三角形
探究新知
第二部分
PART 02
your content is entered here, or by copying your text, select paste in this box and choose to retain only text. your content is typed here
例1 如图,在 Rt△ABC 中,∠C = 90°,∠A,∠B,∠C 所对的边分别为 a,b,c,且 ,求这个直角三角形的其他元素.
解:在 Rt△ABC 中,a2+b2 = c2, , .
A
B
C
典例精析
在 Rt△ABC 中,
在如图的 Rt△ABC 中,根据 AC = 2.4,斜边 AB= 6,你能求出这个直角三角形的其他元素吗?
A
B
C
6
2.4
练一练
解:
问题2 如果已知 Rt△ABC 中一边和一锐角,你能求出这个三角形其他的元素吗?
已知一边及一锐角解直角三角形
例2 如图,在 Rt△ABC 中,∠C=90°,∠A,∠B,∠C 所对的边分别为 a,b,c,且 b = 30,∠B= 25°,求这个直角三角形的其他元素(边长精确到1).
A
B
C
b
30
c
a
25°
解:
在Rt △ABC 中,∠C = 90°,∠B = 25°,
∴∠A=65°.
在图中的 Rt△ABC 中,根据 ∠A=75°,斜边AB=6,你能求出这个直角三角形的其他元素吗?
A
B
C
6
75°
)
练一练
解:
事实上,在直角三角形的六个元素中,除直角外,如果再知道两个元素(其中至少有一个是边),这个三角形就可以确定下来,这样就可以由已知的两个元素求出其余的三个元素.
A
B
a
b
c
C
由直角三角形中已知的元素,求出所有未知元素的过程,叫做解直角三角形.
归纳总结
解:过点 A 作 AD⊥BC 于 D.
在 △ACD 中,∠C = 45°,AC=2,
∴CD = AD = sinC·AC = 2sin45°= .
在 △ABD 中,∠B = 30°,
∴BD =
∴BC = CD+BD = + .
例3 如图,在 △ABC 中,∠B = 30°,∠C = 45°,AC = 2,求 BC.
D
A
B
C
构造直角三角形解决问题
巩固练习
第三部分
PART 03
your content is entered here, or by copying your text, select paste in this box and choose to retain only text. your content is typed here
练一练
如图,在菱形 ABCD 中,AE⊥BC 于点 E,EC=4,
sinB= ,则菱形的周长是( )
A.10 B.20 C.40 D.28
C
1. 如图,在 Rt△ABC 中,∠C = 90°,∠B = 30°,
AB = 8,则 BC 的长是( )
D
2. 在 △ABC 中,AB = AC = 3,BC = 4,则 cosB 的值是_________.
3. 如图,已知 Rt△ABC 中,斜边 BC 上的高AD = 3,cosB = ,则 AC 的长为( )
A.3 B.3.75
C.4.8 D.5
B
4. 在 Rt△ABC 中,∠C = 90°,根据下列条件解直角三角形;
(1) a = 30 , b = 20 ;
解:根据勾股定理得
A
B
C
b=20
a=30
c
(2) ∠B = 72°,c = 14.
A
B
C
b
a
c=14
解:
5. 如图,在 Rt△ABC 中,∠C = 90°,AC = 6, ∠BAC 的平分线 ,解这个直角三角形.
D
A
B
C
6
解:
∵AD 平分 ∠BAC,
∴∠CAB = 60°,∠B = 30°.
6. 如图,在Rt△ABC 中,∠C=90°,cosA = ,
BC = 5, 试求AB的长.
解:
A
C
B
设
∴AB的长为
7. 如图,某人想沿着梯子爬上高 4 米的房顶,梯子的倾斜角(梯子与地面的夹角)不能大于 60°,否则就有危险,那么梯子的长至少为多少米
解:如图所示,依题意可知,当 ∠B = 60° 时,
答:梯子的长至少 4.62 米.
C
A
B
图①
解:∵cos∠B= ,∴∠B=45°,
当△ABC为钝角三角形时,如图①,
∵AC = 13,∴由勾股定理得 CD = 5
∴BC = BD - CD =12-5 = 7.
8. 在 △ABC 中,AB = ,AC = 13,cos∠B = ,求 BC 的长.
当 △ABC 为锐角三角形时,如图②,
BC =BD + CD = 12 + 5 = 17.
∴BC 的长为 7 或 17.
图②
当三角形的形状不确定时,一定要注意分类讨论.
课堂小结
第四部分
PART 04
your content is entered here, or by copying your text, select paste in this box and choose to retain only text. your content is typed here
解直角三角形
依据
解法:只要知道五个元素中的两个元素(至少有一个是边),就可以求出余下的三个未知元素.
勾股定理
两锐角互余
锐角的三角函数
(2) 两锐角之间的关系
∠A+∠B=90°
(3) 边角之间的关系
(1) 三边之间的关系
(勾股定理)
A
B
a
b
c
C
在解直角三角形的过程中,一般要用到下面一些关系:
第一章 直角三角形的边角关系 1.4
解直角三角形
北师大版九年级下册数学课件
第一章 直角三角形的边角关系 1.4
解直角三角形
北师大版九年级下册数学课件
目录
目录
CONTENTS
CONTENTS
1-新知导入
2-探究新知
3-巩固练习
4-课堂小结
新知导入
第一部分
PART 01
your content is entered here, or by copying your text, select paste in this box and choose to retain only text. your content is typed here
A
C
B
c
b
a
(1) 三边之间的关系:a2+b2 = _____;
(2) 锐角之间的关系:∠A+∠B=_____;
(3)边角之间的关系:sinA=_____,cosA=_____,
tanA=_____.
在 Rt△ABC 中,共有六个元素(三条边,三个角),其中∠C = 90°,那么其余五个元素之间有怎样的关系呢?
c2
90°
复习引入
问题1 如果已知 Rt△ABC 中两边的长,你能求出这个三角形其他的元素吗?
已知两边解直角三角形
探究新知
第二部分
PART 02
your content is entered here, or by copying your text, select paste in this box and choose to retain only text. your content is typed here
例1 如图,在 Rt△ABC 中,∠C = 90°,∠A,∠B,∠C 所对的边分别为 a,b,c,且 ,求这个直角三角形的其他元素.
解:在 Rt△ABC 中,a2+b2 = c2, , .
A
B
C
典例精析
在 Rt△ABC 中,
在如图的 Rt△ABC 中,根据 AC = 2.4,斜边 AB= 6,你能求出这个直角三角形的其他元素吗?
A
B
C
6
2.4
练一练
解:
问题2 如果已知 Rt△ABC 中一边和一锐角,你能求出这个三角形其他的元素吗?
已知一边及一锐角解直角三角形
例2 如图,在 Rt△ABC 中,∠C=90°,∠A,∠B,∠C 所对的边分别为 a,b,c,且 b = 30,∠B= 25°,求这个直角三角形的其他元素(边长精确到1).
A
B
C
b
30
c
a
25°
解:
在Rt △ABC 中,∠C = 90°,∠B = 25°,
∴∠A=65°.
在图中的 Rt△ABC 中,根据 ∠A=75°,斜边AB=6,你能求出这个直角三角形的其他元素吗?
A
B
C
6
75°
)
练一练
解:
事实上,在直角三角形的六个元素中,除直角外,如果再知道两个元素(其中至少有一个是边),这个三角形就可以确定下来,这样就可以由已知的两个元素求出其余的三个元素.
A
B
a
b
c
C
由直角三角形中已知的元素,求出所有未知元素的过程,叫做解直角三角形.
归纳总结
解:过点 A 作 AD⊥BC 于 D.
在 △ACD 中,∠C = 45°,AC=2,
∴CD = AD = sinC·AC = 2sin45°= .
在 △ABD 中,∠B = 30°,
∴BD =
∴BC = CD+BD = + .
例3 如图,在 △ABC 中,∠B = 30°,∠C = 45°,AC = 2,求 BC.
D
A
B
C
构造直角三角形解决问题
巩固练习
第三部分
PART 03
your content is entered here, or by copying your text, select paste in this box and choose to retain only text. your content is typed here
练一练
如图,在菱形 ABCD 中,AE⊥BC 于点 E,EC=4,
sinB= ,则菱形的周长是( )
A.10 B.20 C.40 D.28
C
1. 如图,在 Rt△ABC 中,∠C = 90°,∠B = 30°,
AB = 8,则 BC 的长是( )
D
2. 在 △ABC 中,AB = AC = 3,BC = 4,则 cosB 的值是_________.
3. 如图,已知 Rt△ABC 中,斜边 BC 上的高AD = 3,cosB = ,则 AC 的长为( )
A.3 B.3.75
C.4.8 D.5
B
4. 在 Rt△ABC 中,∠C = 90°,根据下列条件解直角三角形;
(1) a = 30 , b = 20 ;
解:根据勾股定理得
A
B
C
b=20
a=30
c
(2) ∠B = 72°,c = 14.
A
B
C
b
a
c=14
解:
5. 如图,在 Rt△ABC 中,∠C = 90°,AC = 6, ∠BAC 的平分线 ,解这个直角三角形.
D
A
B
C
6
解:
∵AD 平分 ∠BAC,
∴∠CAB = 60°,∠B = 30°.
6. 如图,在Rt△ABC 中,∠C=90°,cosA = ,
BC = 5, 试求AB的长.
解:
A
C
B
设
∴AB的长为
7. 如图,某人想沿着梯子爬上高 4 米的房顶,梯子的倾斜角(梯子与地面的夹角)不能大于 60°,否则就有危险,那么梯子的长至少为多少米
解:如图所示,依题意可知,当 ∠B = 60° 时,
答:梯子的长至少 4.62 米.
C
A
B
图①
解:∵cos∠B= ,∴∠B=45°,
当△ABC为钝角三角形时,如图①,
∵AC = 13,∴由勾股定理得 CD = 5
∴BC = BD - CD =12-5 = 7.
8. 在 △ABC 中,AB = ,AC = 13,cos∠B = ,求 BC 的长.
当 △ABC 为锐角三角形时,如图②,
BC =BD + CD = 12 + 5 = 17.
∴BC 的长为 7 或 17.
图②
当三角形的形状不确定时,一定要注意分类讨论.
课堂小结
第四部分
PART 04
your content is entered here, or by copying your text, select paste in this box and choose to retain only text. your content is typed here
解直角三角形
依据
解法:只要知道五个元素中的两个元素(至少有一个是边),就可以求出余下的三个未知元素.
勾股定理
两锐角互余
锐角的三角函数
(2) 两锐角之间的关系
∠A+∠B=90°
(3) 边角之间的关系
(1) 三边之间的关系
(勾股定理)
A
B
a
b
c
C
在解直角三角形的过程中,一般要用到下面一些关系:
第一章 直角三角形的边角关系 1.4
解直角三角形
北师大版九年级下册数学课件
